不同雨量站密度下水文模拟效果分析
杨无双,霍 苒,曾 强,陈 华
(武汉大学水资源与水电工程科学国家重点实验室,武汉 430072)
0 引 言
不同的雨量站密度和空间分布会增加区域降雨量的计算误差[1],从而增加水文模拟结果的不确定性[2]。研究雨量站网密度和空间分布对水文模拟结果的影响,有利于提高模型模拟精度,同时为合理的雨量站网优化设置提供参考[3]。为了分析雨量站网密度的影响,Bardossy和Das[4]利用德国Neckar流域的高密度雨量站网数据,定义了6个雨量站网密度等级,分析了在不同雨量站密度等级下HBV模型的率定和检验效果,结果发现当雨量站数目增加到某阈值后,继续增加雨量站密度对模型模拟效果的改善作用已不再明显。Hongliang Xu[5]等在湘江流域分析了不同雨量站密度等级对新安江模型模拟效果的影响,发现当雨量站数目较少时,面雨量计算误差较大,因而会给水文模型模拟效果带来显著影响。本文以湘江流域为研究区,分析了不同雨量站网密度等级下,雨量站空间分布对区域降雨量计算以及水文模型模拟结果的影响。
1 研究区域与数据
湘江流域地处北纬24°31′~29°00′,东经110°30′~114°00′之间,全流域面积94 660 km2,是洞庭湖水系中最大的河流[6]。流域内水系发达,降水充足,多年平均降水量为1 300~1 500 mm,但年内分布不均。径流主要来源于降水,每年4-9月为汛期,10月至次年2月为枯水期。
本文研究所用水文气象数据是洞庭湖区水文年鉴中摘录的2006-2014年共9年的日降水、日蒸发和日径流实测数据,其中包括252个雨量站点,12个蒸发站点和11个流量站点。水文、气象站地理位置分布如图1所示。本文选择了湘江流域中雨量站点较多且分布相对均匀的衡阳以上流域和湘潭以上流域为研究区域。
2 模型与方法
2.1 新安江模型
新安江模型是在1973年由河海大学赵人俊教授提出的集总式流域水文模型。该模型在国内外湿润半湿润地区的模拟效果普遍较好,应用十分广泛[7-9]。本文研究使用三水源新安江模型,共15个参数,每个参数都具有明确的物理意义[10, 11]。参数说明如表1所示。

表1 新安江模型参数说明Tab.1 Description of Xin'anjiang model parameters
2.2 目标函数
本文采用纳西效率系数(NSE)和水量相对误差(RE)作为模型模拟精度的评价指标。
(1)
(2)
式中:Qsim,i为模拟流量序列;Qobs,i为实测流量序列。
2.3 研究方法
根据湘江流域252个雨量站点,定义了7个雨量站密度等级,每个雨量站密度等级下的站点数目和密度如表2所示[5, 12]。在每个雨量站密度等级下,采用蒙特卡洛随机抽样的方法,从每个子流域包含的站点中随机抽取n组站点组合,每个组合的站点数为该站点密度下相应的站点数目。然后使用泰森多边形法计算各种雨量站组合情况下的2005-2014年的面降雨量,作为新安江模型的输入,并采用SCE-UA算法率定模型参数得到模型输出结果[13, 14]。通过分析模型参数和模拟的流量过程,研究不同雨量站网密度下,雨量站网空间分布对水文模拟结果的影响。

表2 雨量站密度等级划分Tab.2 Density classification of rainfall station
3 研究结果与讨论
3.1 给定站网密度下随机抽样次数的选取
对于给定站网密度,当抽样次数较少时,所抽取的雨量站组合样本并不能完全反映出雨量站空间分布的差异,比如所有样本中的雨量站都集中在流域某个小区域内,这将导致估计的面降雨量出现系统偏差。图2给出了随机抽取10次、100次和200次时,各子流域在不同雨量站密度下,年均降雨量的箱线图。从图2中可以看出,当仅随机采样10次时,年均降雨量的分布范围较窄,而且随着站点数的增加,年均降雨量的分布范围并不严格呈现减小的趋势,中值也与用子流域中所有站点计算出的年均降雨量差异较大,说明仅仅10次采样不足以完全反映出雨量站空间分布的差异。当随机采样次数增加到100次以后,两个子流域中100次采样与200次采样的面均降雨箱线图已经没有太大差异,而且随着站点数目的增加,面均降雨量的分布范围逐渐减小,说明采样数目在100次以上已经能够充分反映出雨量站空间分布的差异,满足研究雨量站空间分布差异对水文模拟的影响的要求。为了尽可能地减小抽样次数对模拟分析的影响,本文选择200作为每个子流域,各雨量站密度下的采样次数。
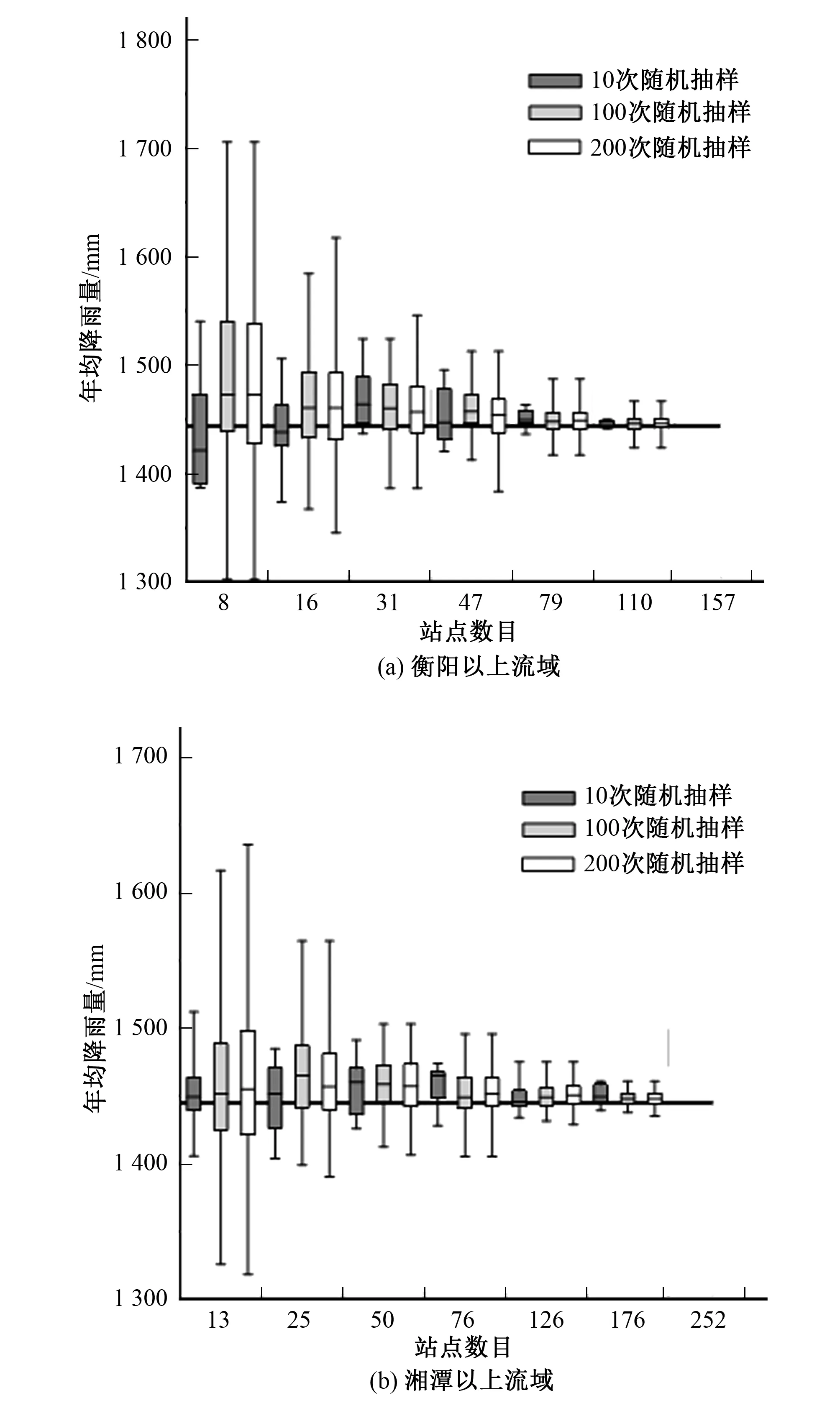
图2 各子流域在不同采样次数下年均降雨量箱线图Fig.2 The annual average rainfall box-plot of each sub-basin under different sampling times 注:图中箱线的横线分别表示最小值,25%分位数,中值,75%分位数,和最大值。
3.2 不同雨量站网密度对水文模型模拟结果的影响分析
对于两个子流域,在不同的雨量站网密度等级下,将3.1节随机抽取的200组雨量站组合通过泰森多边形法计算得到的面均降雨作为新安江模型的输入。然后采用SCE-UA算法率定模型参数,得到对应的200组模型最优参数,以及200组模拟流量序列。通过比较不同雨量站密度和空间分布条件下,模型的最优参数和输出结果,分析雨量站网差异对水文模型结果的影响。
(1) 模型参数分析。计算新安江模型每个参数的方差并归一化,结果如图3所示。可以看出,图3(b)中参数EX和IMP表现出与其他参数不同的趋势,这主要是由于新安江模型参数间强烈的相关性导致的。在新安江模型中,EX描述了流域产流面积上自由水蓄水能力的分布,其值受参数自由水蓄水容量SM影响较大[15]。当站点数从25增加到50的时候,尽管参数EX的方差有所增加,但是总的来看,参数SM和参数EX总体的方差是随着降雨站点数目的增加而减小的。对于参数IMP,其反映了流域的不透水面积比例,当雨量站个数从13增加到176时,参数IMP的均方差变化范围仅为0.002 3~0.002 7,说明参数IMP对雨量站网密度及分布的反应并不明显,所以在图3(b)中呈现了不同趋势。总的来说,随着雨量站数目的增加,两个子流域新安江模型参数的方差逐渐减小。这意味着,通过增加雨量站的密度,可以有效减小雨量站空间分布的差异对模型参数估计的影响。
(2) 评价指标分析。对于各雨量站密度等级,计算200组新安江模型模拟流量系列的纳西效率系数和水量相对误差,评价指标箱线图如图4所示。从图4中可以看出:①随着雨量站密度的增加,模型的模拟效果显著上升,且模型的评价指标的分布逐渐变窄,说明可以通过提高雨量站网密度来减小站点分布差异对模型模拟精度的影响,使模型的表现更稳定;②当站点密度达到一定阈值之后,模型的精度提高缓慢,说明过密的雨量站对模型模拟效果的提升并没有明显的帮助;③当站点密度较低时,尽管大部分站点组合方式都不能得到较好的水文模拟效果,但是仍然存在部分雨量站网组合可以得到较好水文模拟结果,比如站点数为8时,纳西效率系数最大值为0.89。这说明除了增加雨量站数目外,优化雨量站空间分布也能提高水文模型模拟精度;④从衡阳站和湘潭站的水量相对误差结果可以看出,当站点密度较小时,模型更容易低估水量,这主要是因为雨量站数目较小时,站网难以捕捉到局部地区的对流雨,使得输入模型的面降雨量偏小。
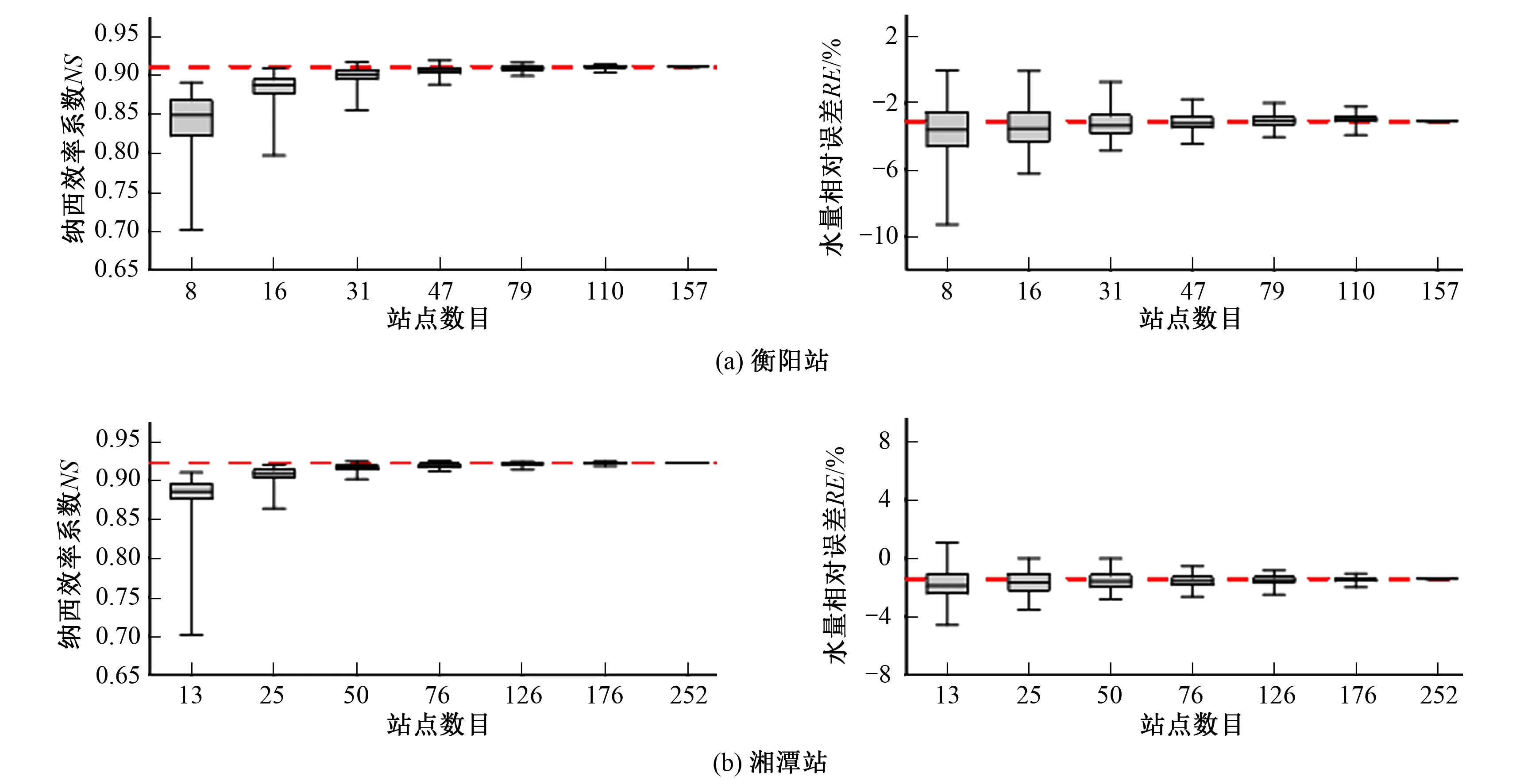
图4 不同雨量站密度下,新安江模型评价指标箱线图Fig.3 Box-plot of evaluation index of Xin'anjiang model under different rainfall station densities
(3) 径流模拟分析。本文通过比较不同雨量站点组合情况下,模拟流量系列的流量相对历时曲线与实测流量系列的流量相对历时曲线的关系,分析雨量站密度与空间分布对径流模拟的影响[16]。图5、图6分别给出了200种雨量站组合情况下,新安江模型在衡阳站、湘潭站的模拟流量相对历时曲线和10年日实测流量的相对历时曲线。对比分析两图可以看出,各站点密度条件下,高水部分的95%置信区间较低水部分普遍更宽,说明雨量站空间分布的差异对高水部分水文模拟影响更为显著。随着雨量站点数目的增加,模拟的流量历时曲线95%置信区间宽度逐渐变窄,说明当采用更多的雨量站数据率定模型参数时,高水部分的模拟受到雨量站分布影响会显著减小。

图5 不同雨量站密度下,新安江模型衡阳站模拟流量相对历时曲线图Fig.5 Relative flow-duration curve of simulated runoff at Hengyang Station of Xin'anjiang Model under different rainfall station densities

图6 不同雨量站密度下,新安江模型湘潭站模拟流量相对历时曲线图Fig.6 Relative flow-duration curve of simulated runoff at Hengyang Station of Xin'anjiang Model under different rainfall station densities
4 结 语
本文对湘江流域定义了7 个雨量站等级,对每个等级采用随机抽样的方法,抽取200 组雨量站组合情况,并将每种雨量站组合情况下的泰森多边形面降雨计算结果作为新安江水文模型的输入,采用SCE-UA算法率定模型参数,模拟衡阳、湘潭站的流量过程,分析了模型参数和模拟结果对雨量站密度和空间分布的响应。主要结论如下。
(1) 提高雨量站网密度能够有效降低模型最优参数的估计误差,使得模型在不同的雨量站空间分布下具有稳定的表现和良好的模拟精度;
(2) 当雨量站数目增加到一定阈值后,从模拟精度的评价指标纳西效率系数和水量相对误差分析,模型的模拟效果提升不再明显;
(3) 随着雨量站网密度增加,对高水部分的模拟影响呈减小的趋势;
(4) 雨量站密度较小时,仍然存在部分雨量站网组合可以得到较好水文模拟结果。
□

