巧记特殊四边形的判定

赵小霞

四边形是八年级数学的一个重点和难点，本章内容繁多，很多初学者难以理解和记忆，下面我介绍一种便于同学们记忆和理解的方法——“找不同”加“图示记忆法”。

学习数学，尤其是数学中的几何问题，离不开数形结合思想，下面我通过图示来帮助同学们记忆特殊四边形的判定。

首先由四边形到平行四边形，我们只需要把平行四边形的性质反过来就会得到平行四边形的判定方法。

先从平行四边形的“边”上来考虑：位置关系-平行，数量关系-相等，我们很容易找到边上的三条判定：（1）两组对边分别平行的四边形是平行四边形，（2）两组对边分别相等的四边形是平行四边形，（3）一组对边平行且相等的四边形是平行四边形四边形。巧记口诀：“两平行、两相等、一组平行且相等”，这样边上的三条判定就记住了！ 然后再从“角”上和“对角线”上来考虑：把性质反过来不难得出：（4）两组对角分别相等的四边形是平行四边形，（5）对角线互相平分的四边形是平行四边形，这样平行四边形的五条判定方法就得到了！

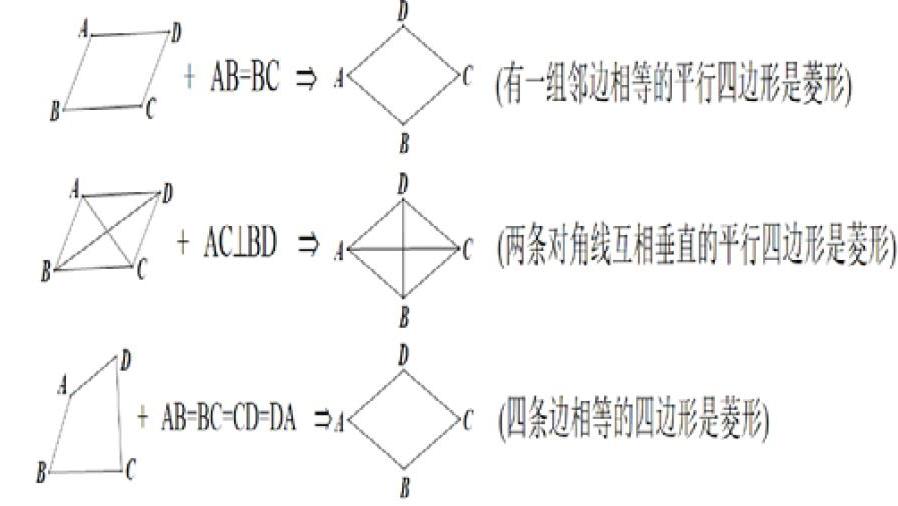
由平行四边形到矩形或由平行四边形到菱形的判定可以正式用上“找不同”的方法找到所有的判定条件。拿平行四边形到菱形的判定来说：先从“边”上对比平行四边形和菱形，对边都是平行且相等，而菱形的邻边也相等，所以只需要在平行四边形的基础上加上一组邻边相等就可以得到菱形;从“角”上来考虑，平行四边形和菱形都是对角相等、邻角互补，没有什么不同的，所以在角上找不出判定条件;然后从“对角线”上来分析，平行四边形的对角线互相平分，而菱形的对角线既平分又垂直，所以我们找到了它的不同点：少了垂直，因而在平行四边形的基础上，加上对角线互相垂直就可以得到菱形。 这是以平行四边形为起点来判定菱形的，若以四边形为起点，考虑到菱形的四条边都相等，把这条性质反过来就得到了由四边形直接判定为菱形的方法：四条边都相等的四边形是菱形。这样我们就找到了三种菱形的判定方法，再利用“图示记忆法”，可以轻松的将这三条判定方法记住：

我们再用这种方法来找一下由平行四边形到矩形的判定：

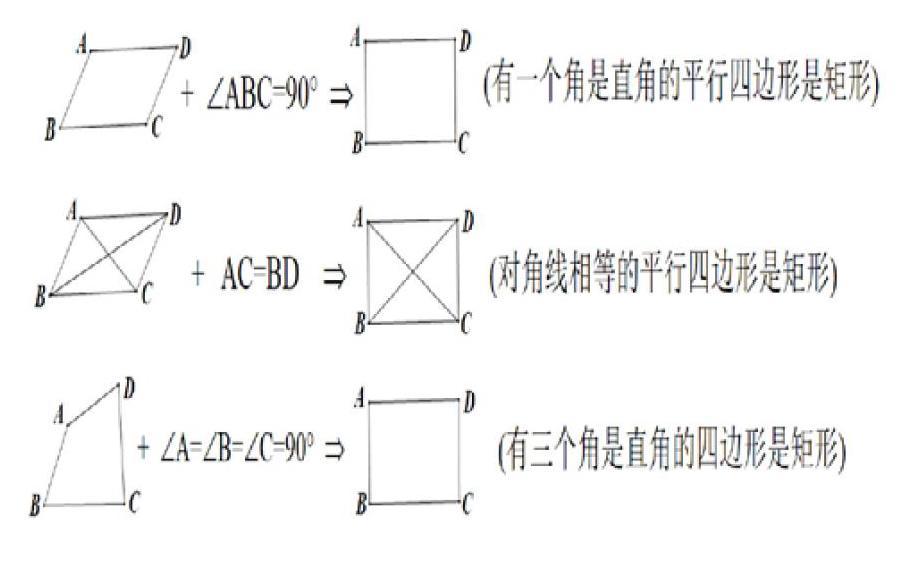
首先“边”上平行四边形和矩形都是对边平行且相等，邻边都不一定相等，没有不同，所以在边上没有判定方法;再从“角”上来看，矩形的内角是90°，而平行四邊形则不一定，所以在平行四边形的基础上，只要加上一个角是90°，我们就可以得到矩形;然后再从“对角线”上来分析，平行四边形的对角线互相平分，而矩形的对角线即平分又相等，所以在平行四边形的基础上加上对角线相等就可以得到矩形;由于矩形的四个角都是直角，所以把这条性质反过来，只要有三个角是直角的四边形就是矩形，这样以四边形为起点就判定出了矩形。矩形的三条判定利用“找不同”的方法就能找到了，然后利用“图示记忆法”，可以轻松的将这三条判定方法记住：

按照上述方法，从边、角、对角线三个角度我们也很容易找到从矩形到正方形和从菱形到正方形的判定方法，图示如下：

四边形中众多的判定方法，我们只需要从边、角、对角线三方面对比“找不同”就可以找到所有特殊四边形的判定方法，再利用“图示记忆法”就可以快速准确的记忆，同学们可以试一试！