基于谐波小波包和改进功率谱的球磨机振动信号特征提取
李 珏,高云鹏,卿宗胜,杨佳伟,王庆凯,李文博
(1.湖南大学电气信息与工程学院,湖南长沙 410082;2.矿冶过程自动控制技术国家重点实验室,北京 100160;3.矿冶过程自动控制技术北京市重点实验室,北京 100160)
0 引言
球磨机负荷是球磨机筒体内部钢球、矿料、水的总和[1],球磨机负荷的准确检测能有效指导磨矿过程的优化控制,是选矿行业磨矿生产过程中的一个重要参数。然而在实际生产过程中,矿石性质、球磨机运行状态等具有的时变性、复杂性和耦合性[2]使得球磨机负荷的准确预测难以实现。客观、准确提取球磨机外部响应信号特征,通过对负荷变化敏感的特征参数及时掌握球磨机的内部负荷状态,可保障球磨机的安全可靠运行,实现节能降耗。
球磨机振动信号包含丰富的球磨机运作状态信息,球磨机内部负荷的变化可通过振动有效表现。相较于功率法、差压法和噪声法等方法,振动法具有灵敏度较高、传感器安装简便的特点,是当前工业应用的主要测量方法[3-5]。文献[6]将球磨机振动信号小波包分析后得到的能量幅值作为特征参数,受噪声干扰较大。文献[7-8]基于全部频谱来选择特征频段,未选频段会导致重要信息缺失,且所选频段不具备明确的物理意义。文献[9]以分频段能量值作为对应内部负荷的特征向量,其有效性仅在小型实验球磨机上得到了验证。小型球磨机振动信号与工业球磨机振动信号差异很大,对于工业生产应用,寻求工业球磨机振动信号的更能有效表征球磨机负荷的特征值更具实际价值。
本文根据小波变换的多分辨率分析的特点,采用谐波小波包分解,将工业球磨机振动信号功率谱分解到不同频段,提取各频段功率谱层最大值对应频率作为信号特征,定量分析各特征参数随球磨机负荷的变化规律,并通过实测数据实验结果证明了本文提出方法的有效性和准确性。
1 谐波小波包分解
球磨机通过研磨介质对矿物不断撞击与冲击,使矿物粒度逐渐变小,实现磨矿的目的,其产生的振动信号具有非平稳非线性的特点。小波分析作为一种时频分析手段,被广泛应用于时变非平稳振动信号的去噪、特征提取、故障识别等领域[10]。本文首先应用谐波小波包分解对球磨机筒体振动信号进行分析处理。
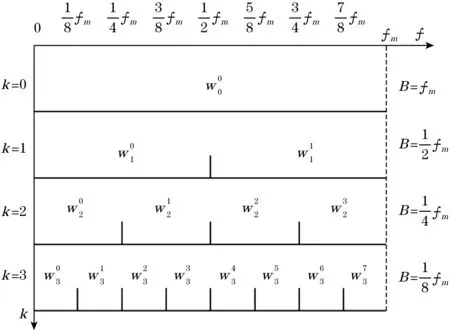
谐波小波[11]由频域进行构造,其频域表达式为
(1)
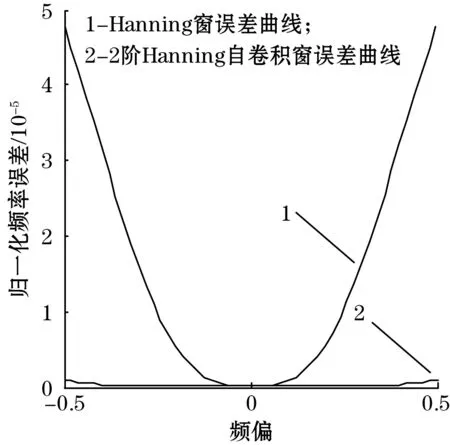
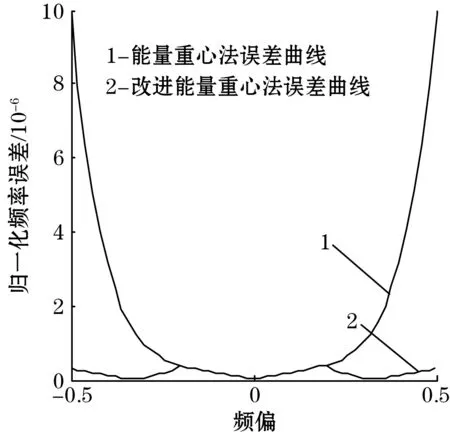
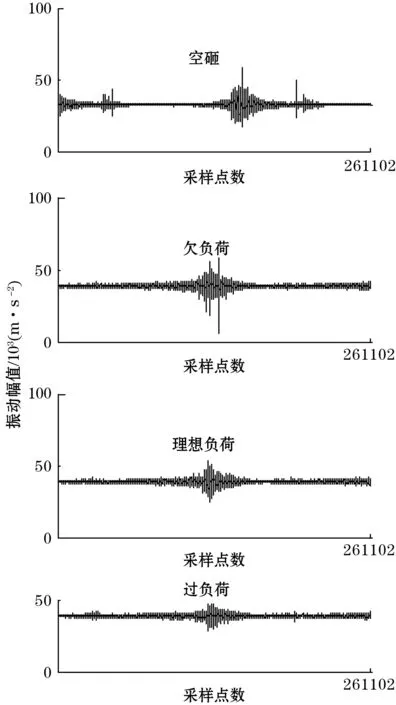
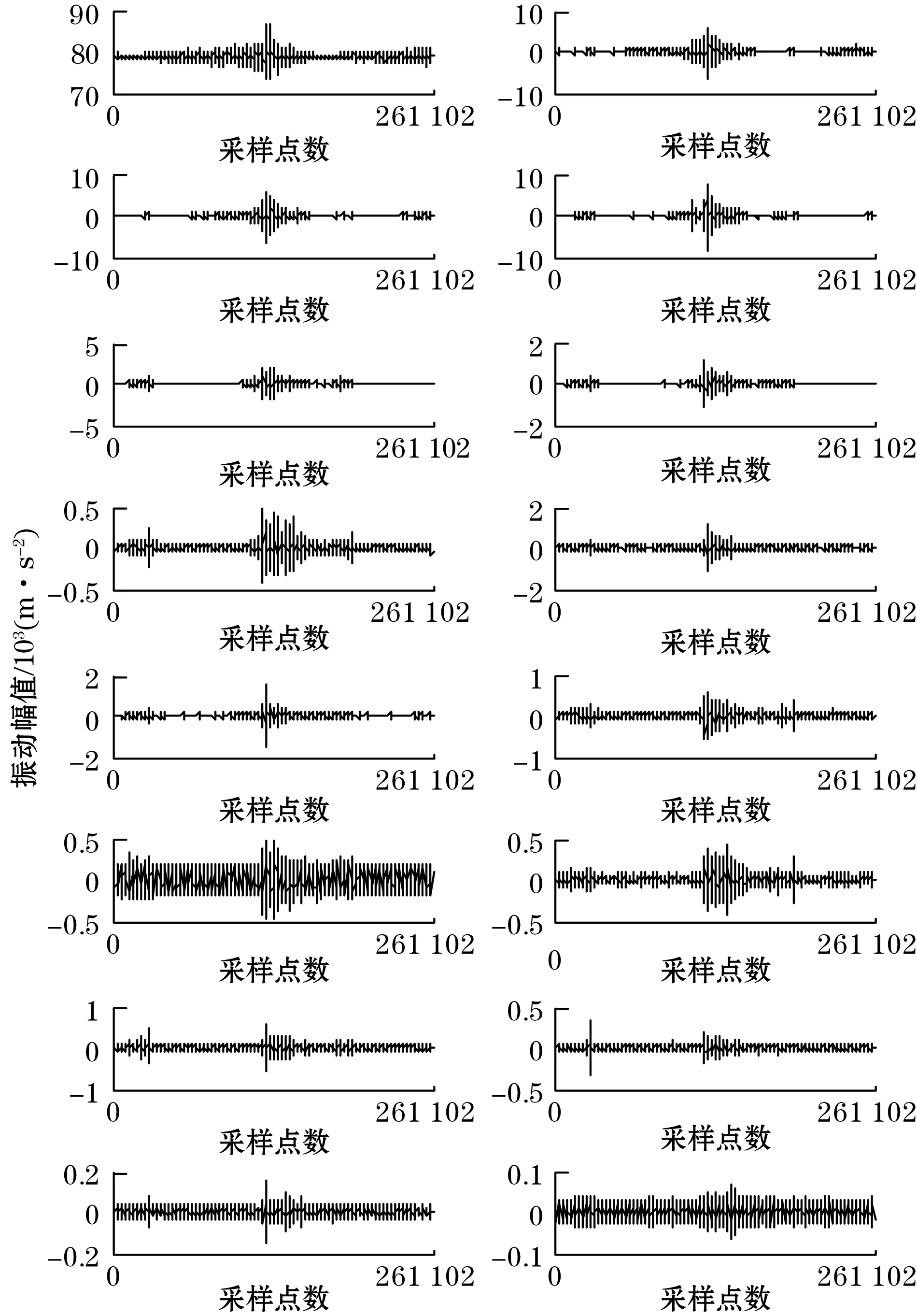
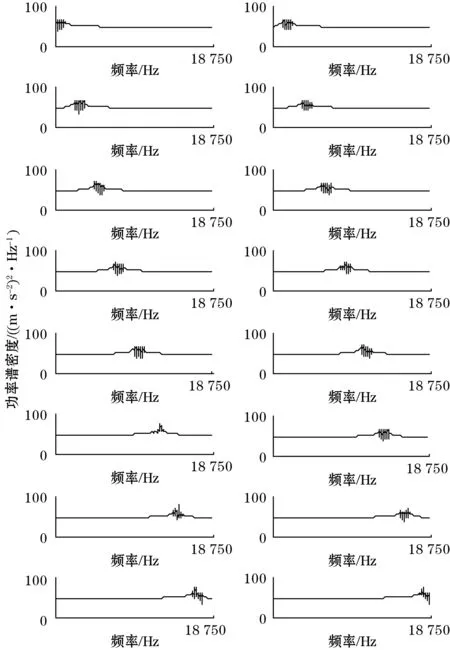
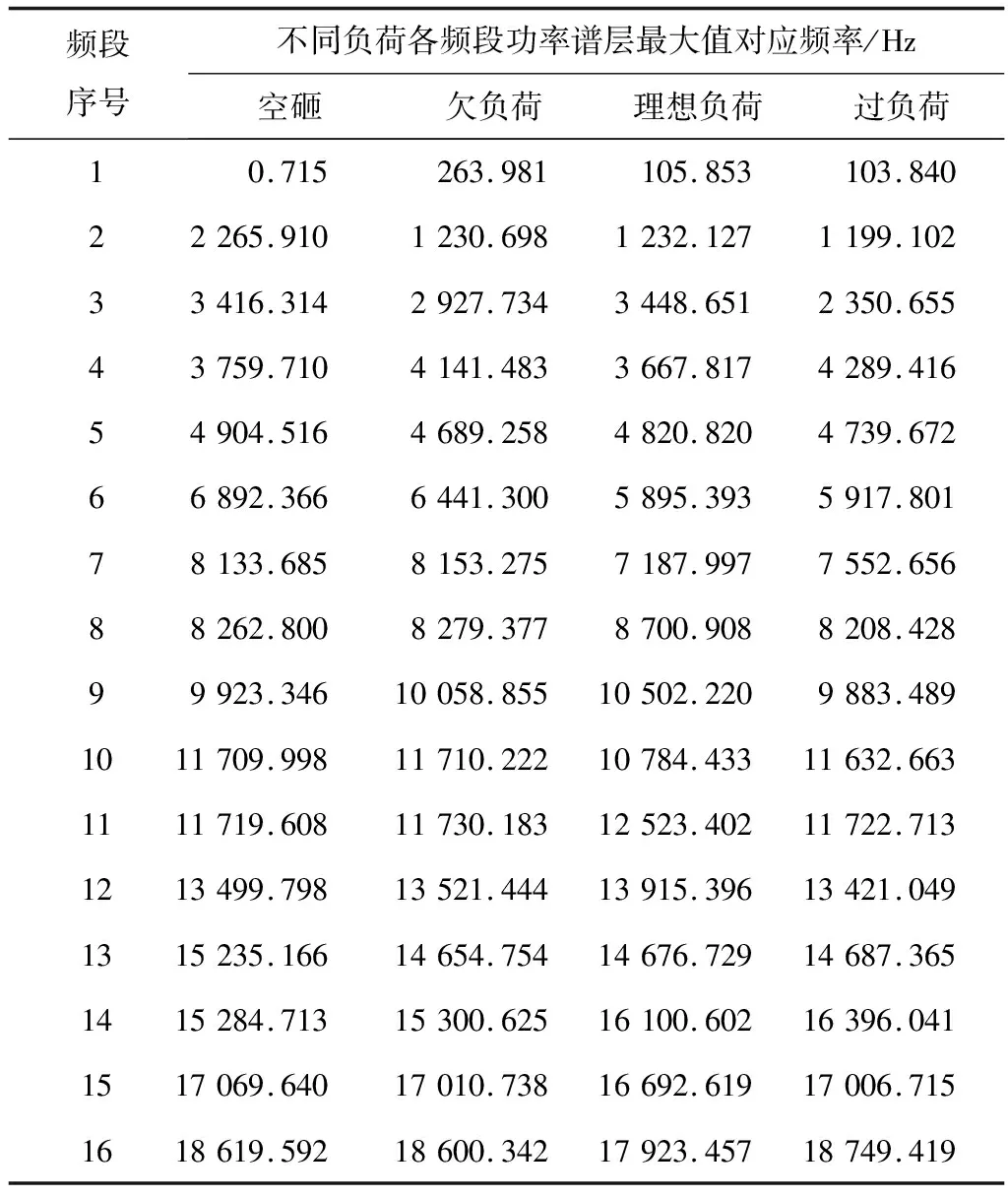
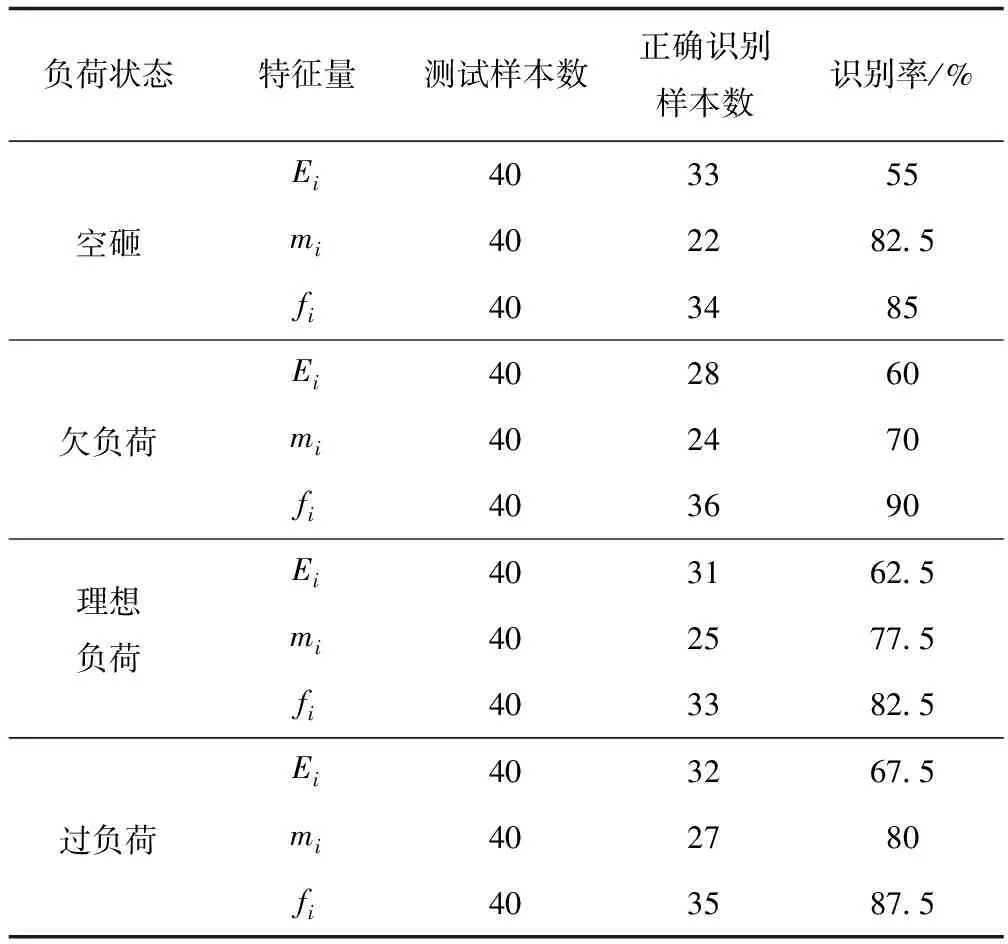
式中:m、n为正实数,且m 对式(1)进行逆傅里叶变换,得其时域表达式为 (2) 图1 谐波小波包分解频域分布 B=fm/2k (3) (4) 由图1可知,若对某频段信号深入分析,可将信号分解到对应层,有利于更好进行信号的特征提取。 功率谱密度可反映随机过程振动能量在各个频率域上的概率分布[14]。本文选用自相关法功率谱估计,求取球磨机振动信号功率谱,即由随机信号的N个观察值估计出自相关函数rN(m),并以rN(m)的傅里叶变换作为功率谱估计,其计算公式为 (5) 间接法功率谱估计首先需要得到随机信号的自相关函数。对于确定信号离散采样序列x(n)(n=1,2,…,N-1),其自相关函数为 (6) 对于各延时τ(τ>0),可利用数据仅为N-1-τ个,在实际计算中,式(6)变为 (7) 如图2所示,首先将信号x(t)离散后序列x(n)的长度取为2N,自相关函数长度取为N,令延时τ在(0,N-1)上移动时,进行相关求和的数据长度始终为N。采用改进自相关法可有效改善衰减,得到的波形更平滑,再对求得的自相关函数进行加窗插值FFT计算,即可得到信号的功率谱,结合性能较好的窗函数,进行功率谱校正,据此减少频谱泄漏对计算结果的影响。 图2 改进自相关原理 能量重心法[15]利用离散窗谱函数的能量重心为坐标原点的原理得到频率校正量,能对多段平均功率谱进行校正,具有算法简便、计算快的优点。 对于单一谐波信号等间隔采样序列: x(n)=A0cos(2πf0n/N+θ0) (8) 式中:f0为频率;A0为幅值;θ0为相位;N为采样点数;n=0,1,2,…,N-1。 其加窗傅里叶变换为 (9) 式中:w(n)为窗函数;k=0,1,2,…,N-1。 (10) 式中δ为归一化频率偏差,简称频偏,且-0.5≤δ≤0.5。 令G(i)为加窗信号功率谱第i条谱线值,k0对应主瓣内峰值谱线,若窗函数满足离散频谱能量重心无穷逼近坐标原点这一特性,当n→∞时有: (11) 由式(11)可得主瓣中心: (12) 则其频率校正公式为 (13) 式中fs为采样频率。 能量重心法通过选取主瓣内谱线实现校正,适用于频率间隔较远的多频率成分信号,而对于密集或连续频谱信号校正精度不高。 本文从窗函数角度出发,结合余弦自卷积窗具有随卷积阶数增加旁瓣峰值电平更低、旁瓣衰减速率更快,更易区分相邻的密集频率信号的特点,构造2阶Hanning自卷积窗,将其引入能量重心法,提高能量重心法应用在频率成分密集信号的分辨率。 电池的循环性能和倍率性能在多通道电池测试系统上进行,循环性能测试的充放电工作电压范围为2.5 ~ 4.0 V。电池的循环伏安(CV)测试和交流阻抗(EIS)测试在电化学工作站上进行。CV用于研究活性材料的电化学变化及动力学参数等,测试时扫描电压的范围为2.5 ~ 4.0 V,扫描速率为0.2 mV/s。EIS用于测试不同组分的阻抗大小,其测试的频率范围为0.01 ~ 100 kHz,交流信号振幅为5 mV。 Hanning窗的频谱模函数为 (14) 根据卷积定理,2阶Hanning自卷积窗函数的频谱模函数为 (15) 则2阶Hanning自卷积窗函数的窗谱能量表达式为 (16) 数学推导可证,2阶Hanning自卷积窗满足能量重心法所需窗函数性质。 为既保证主瓣内能量较大的谱线都被利用,又减少旁瓣对结果的影响,应用主瓣宽度为4的Hanning窗通常采用5谱线进行频谱校正,则对主瓣宽度为8的2阶Hanning自卷积窗,本文采用7谱线进行频谱校正,则加2阶Hanning自卷积窗能量重心法的频率校正式为 (17) 为证明2阶Hanning自卷积窗能够实现能量重心法精度的提高,以幅值A=1,数据长度N=4 096的单频正弦信号为研究对象,采样频率fs=1 024 Hz,频率分辨率为Δf=fs/N= 0.25 Hz。令信号对象频率f在一个频率分辨率区间[100 Hz,100.25 Hz]上等间隔取51个频率点,分别计算在不同频偏下,加Hanning窗和加2阶Hanning自卷积窗后的能量重心法在这些位置进行校正的结果与真实频率的误差。在每点进行500次仿真,计算平均的归一化频率误差。结果如图3(a)所示。 由图3(a)可看出,2阶Hanning自卷积窗的校正精度远高于Hanning窗。同时也可看出,频偏δ是影响能量重心法频率估计精度的主要因素。据此,由频偏δ所在区间出发,通过对信号进行频移,使得频移后的信号频率尽可能靠近功率谱最大值谱线,再使用能量重心法进行频率估计,可保证获得较高的校正精度。频偏后能量重心法频率校正式为 (18) 式中:fd′ 为信号频移后的频率校正值;N为信号点数;δd为频移距离;r为信号频移方向,若δ∈[-0.2,0.2],r=0;δ∈[-0.5,-0.2),r=1;δ∈(0.2,0.5],r=-1。 由于δ与信号频率有关,为不确定值,每次对信号频移都需计算复指数ej2πrδd/N,为减少计算量,本文将频移δd设为固定值1/3,这样频移后对应的频偏仍可位于校正精度较高的区间上,则修正能量重心法频率校正式为 (19) 频偏后的能量重心法与原始能量重心法的归一化频率误差如图3(b)所示。 (a)加Hanning窗与加2阶Hanning自卷积窗误差曲线 (b)能量重心法与改进能量重心法误差曲线 由图3(b)可知,频偏法可保证信号的频偏位于能量重心法校正精度较高的区间上,使得能量重心法频率校正精度显著改善。 为验证本文方法,将其应用到实验中进行验证。实验对象为山东黄金集团焦家金矿选矿厂磨浮车间的溢流型球磨机(MQYΦ5.5×8.5 m),通过在球磨筒壁进料端1/3处的螺栓上安装加速度传感器获得振动信号,fs=37.5 kHz,在球磨机工作时,利用加速度传感器分别对空砸、欠负荷、理想负荷、过负荷4种球磨机负荷状态进行振动信号采集,4种负荷状态下的振动信号典型时域波形如图4所示。 图4 不同负荷状态振动信号时域波形 由图4可知,在4种不同球磨机内部负荷状态下,振动信号具有一定的随机性,波形总体上呈现为一个中间大两头小的纺锤形状,均出现了明显的冲击分量,但时域信号受噪声影响较大,仅通过振动信号时域波形很难识别出球磨机的内部负荷状态。从采集到的球磨机振动信号中选择空砸、欠负荷、理想负荷、过负荷运行状态各40组样本,数据采样点数均为261 102个,共计160组样本实验数据,分别用Welch法求分频段功率谱能量值Ei、求分频段功率谱层最大值mi和本文方法求分频段功率谱层最大值对应频率fi对该160组样本振动信号进行特征提取。综合考虑频带宽度及分辨率,对球磨机振动信号进行谐波小波包分解为16个频段,各频段频率分析宽度为1 171.875 Hz。以理想负荷下的球磨机振动信号为例,得到的各频段小波系数如图5所示。 图5 理想负荷振动信号各频段小波系数 采用本文提出的改进功率谱估计算法对理想负荷状态振动信号各频段小波系数进行功率谱求取并进行频谱校正,各频段功率谱如图6所示。 图6 理想负荷振动信号各频段功率谱 对不同负荷状态的振动信号,将分频段功率谱层最大值对应的频率fi作为特征向量,各负荷状态的结果均值如表1所示。 为验证利用本文方法提取的特征量的有效性,构造基于支持向量机(support vector machines,SVM)的分类器进对Ei、mi、fi3个特征向量进行测试。构造4个基于SVM的分类器(SVMk,k=1,2,3,4)分别用于识别球磨机内部负荷为空砸、欠负荷、理想负荷、过负荷状态下的振动信号。SVMk的输入向量分别为Ei、mi、fi;输出信号表示为+k或-k,+k表示该分类器识别出该负荷状态,-k表示振动信号未被识别。160组信号样本参与各个SVM的训练和测试,测试样本的识别结果如表2所示。 表1 不同负荷振动信号fi特征向量表 由表2可知,3个特征向量对测试样本的平均识别率分别为61.25%,77.5%,86.25%。特别需要指出的是,在分别识别以上4类负荷状态对应的振动信号时,采用本文方法提取的特征量被误识别的概率更小。例如,识别球磨机处于过负荷状态下的振动信号时,采用特征向量Ei、mi被误识别为球磨机处于理想负荷状态下的振动信号,而采用特征向量fi则未被误识别。基于本文方法得到的特征向量的识别率均大于其他特征向量的识别率,即本文所提出的的特征向量具有更好的类可分性。本文提出的方法通过谐波小波包分解细化频带范围,结合改进自相关和能量重心法,具有良好的抗噪性能和准确性,提取出来的特征向量拥有优于其他方法所提取特征量的区分度。 表2 不同负荷各特征向量识别结果 本文针对工业球磨机振动信号的特点,提出应用谐波小波包分解和对功率谱估计进行改进,提取振动信号特征的方法。采用的谐波小波包分解不仅具有谐波小波的优良特性,更突破其在频带划分上的局限性,实现了更方便和精细的振动信号分解。在对功率谱估计进行改进上,利用移位相加对自相关函数进行改进,对自相关函数加2阶Hanning自卷积窗进行DFT,结合频偏法应用于能量重心法对得到的功率谱进行频谱校正。该方法能快速方便地得出更精确的特征量,同时更加适用于工业现场具有噪声干扰的情况。实验结果表明,该方法能较快且有效提取球磨机振动信号特征向量并能正确地进行负荷状态识别及分类。
2 改进功率谱估计算法
2.1 改进自相关函数

2.2 修正能量重心法
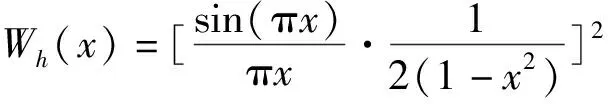
3 实验与分析
4 结束语

