考虑动车组接续的高速铁路列车运行实时调整

占曙光

考虑动车组接续的高速铁路列车运行实时调整

占曙光

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 综合交通运输智能化国家地方联合工程实验室，成都 611756）

在列车运行受干扰条件下，如何快速有效地调整被干扰的列车，使其尽快恢复正常运行，是铁路行车组织的重要工作。本文针对高速铁路受干扰影响导致某区间在一段时间内部分丧失通过能力的情况，建立考虑动车组接续的列车运行调整混合整数线性规划模型，采用商业优化软件CPLEX对模型进行求解。以京沪高速铁路为例，基于假设的列车运行干扰场景对模型进行测试，获得各干扰场景下的列车运行调整方案。结果表明，本文方法能为高速铁路现场调度员提供在动车组运用层面仍可行的列车运行调整图，协助他们的调度决策。

高速铁路；运行干扰；实时调整；动车组运用；混合整数线性规划

0 引 言

高速铁路在日常运营中受各种干扰因素影响[1]，导致线路区间一段时间部分丧失通过能力，列车不能按计划运行图运行。在这种情况下，需要调度员及时调整被干扰的列车，确保行车安全，减小干扰对列车运行的影响。当前，干扰下的高速铁路列车运行调整以调度员人为调整为主，工作压力大。本文采用数学优化的方法为调度员提供干扰下的列车运行调整方案，减轻其工作压力。国内既有研究主要停留在运行图调整层面，尚未考虑动车组接续约束。但是，当列车运行受干扰导致线路部分丧失通过能力时，仅对列车运行图进行调整不够，可能会导致在新的运行图下，部分列车无可用动车组来承担运输任务。为了获取更切实可行的列车运行调整方案，需同步调整列车运行图与动车组运用计划。

虽然为应对日常行车组织中可能出现的事故，提高动车组运用计划的鲁棒性，在大型动车段（所）配有一定数量的备用动车组。但是，为减小铁路投资，备用动车组数量有限。当铁路受干扰导致线路通过能力部分丧失时，运输组织形式发生改变，延长了列车旅行时间，相应地延长了动车组在途时间，因此可能导致原动车组接续计划不可行。此外，部分列车可能被取消运行，列车间动车组接续方案会发生改变。在调整运行图时，综合考虑动车组运用调整非常必要。

近年来，干扰下列车运行实时调整问题引起了国内外学者浓厚的研究兴趣[2]，然而，既有研究主要集中在运行图调整层面，如文献[3-8]。国内少量学者在考虑适当调整运行图基础上对动车组运用进行调整[9]，但是，同时优化运行图和动车组的研究比较缺乏。国外有部分学者对该问题展开研究[10]，但是，国外动车组运用方式与我国不同。因此，在线路通过能力部分丧失下，将动车组运用和运行图调整结合优化，从而得到较切实可行的列车运行调整方案是目前亟待研究的方向。本文在文献[8]基础上，考虑动车组接续约束，对干扰下高速铁路列车运行图进行调整，为现场调度员及时提供在动车组运用层面仍可行的列车运行调整方案。

1 问题描述

1.1 问题定义

文中高速铁路受干扰而区间通过能力部分丧失，指双线高速铁路因干扰导致某区间一条线路在一段时间内不能行车。当线路区间通过能力部分丧失时，铁路现场常组织双向列车在干扰区间共线运行，但是，我国高速铁路现场组织列车在干扰区间反向运行时，规定只能按“站间控制”模式行车，不允许反向列车追踪运行。本文结合我国高速铁路实际情况，对区间通过能力部分丧失下的列车运行调整问题进行研究。

当高速铁路某区间受干扰而通过能力部分丧失时，列车不能按计划运行图运行，调度员需根据当前的列车运行状况信息和现场干扰信息，快速调整被干扰的列车。确定被干扰的每列车在每个车站的到发时刻，同向多列车之间的运行顺序，对向列车在干扰时段通过干扰区间的顺序和是否有列车取消运行。在做上述决策时，调度员需充分考虑各种设备能力约束（包括动车组接续能力约束）和列车运行规则，编制在动车组运用层面仍可行的列车运行调整方案，减小干扰对列车运行的影响。

1.2 问题假设

本文所做的假设如下：

（1）高速铁路中间站的到发线按上下行分别使用，各条到发线均配有供旅客上下的站台，上下行正线与车站各条到发线均相连。

（2）双线高速铁路的每条线路均具备组织双向行车条件，然而，上下行列车在正常情况下分线运行，互不干扰。

（3）故障发生时已经进入故障区间的列车通过了故障点，可继续向前运行。

（4）不考虑动车组检修（假设其发生在晚上）,处于运用状态的动车组在白天均能正常使用。

2 模型构建

2.1 事件-活动网络

图1 事件-活动网络示意图

2.2 基本模型

2.2.1 符号和决策变量说明

模型中参数和决策变量分别如表1、2所示。

表1 各参数定义

Tab.1 The definition for parameters

表2 决策变量定义

Tab.2 The definition for decision variables

2.2.2 基本模型构建

针对两种速度等级列车共线运行的情况进行研究，但是，文中方法也能处理只有单一速度列车运行的情况。干扰下对高速铁路列车运行进行调整的主要目标为：列车尽可能少偏离原始运行计划。从列车运行角度体现为两个方面：最小化列车在车站到发偏离时间。为便于区分，称列车早于计划时刻到达车站为早点，铁路现场将早到也称为晚点。相比于列车早点，旅客更关心列车晚点，所以，应给列车晚点时间更大的惩罚系数；最小化取消列车数量，虽然取消列车运行能消除晚点，但是，会对旅客出行造成极大的影响，因此，取消列车应慎重。从动车组周转的角度，需使动车组之间尽量保持原始的接续关系。综上，模型目标函数考虑了列车取消惩罚量、运行偏离原计划惩罚量及动车组运用计划偏离惩罚量，最小化这三部分惩罚量的加权求和。基本模型建立如下：

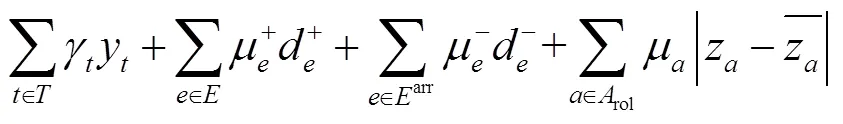
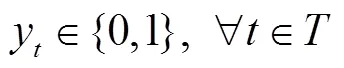
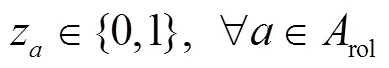
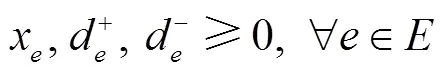
2.3 其他约束条件

考虑动车组接续的列车运行调整问题约束可分为两大类：列车运行相关约束和动车组接续约束。前者在文献[8]中已阐述，关于单列车运行和停站约束、相邻列车运行间隔约束和车站能力约束请参看文献[8]中约束（11）~（19），本文省略该部分内容。

本文采用类似文献[10]中的方法建模动车组接续约束，读者可以参看文献[10]详细了解本建模方法。由于本文是从宏观层面对列车运行进行调整，在考虑车站能力约束时主要考虑到发线能力约束，没有从微观层面去考虑车站咽喉区的能力约束。

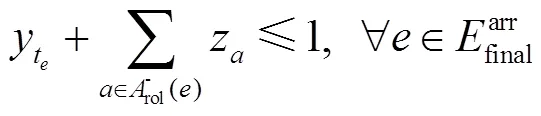
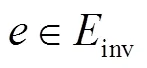
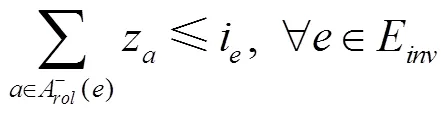
列车到达车站后，其动车组必须要经过一定的准备作业，才能继续担当下一趟列车的运输任务。动车组在接续站的折返时间须满足最小接续时间约束，可建模如下：

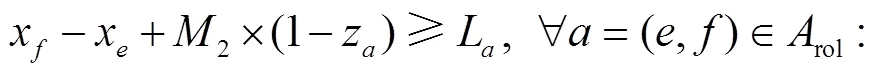
3 算法设计

模型通过对目标函数进行线性化之后，属于混合整数线性规划模型。对于中小规模的问题可以采用有效的商业优化软件CPLEX直接求解最优解或近似最优解[7]，对于规模较大的问题可以采用多阶段算法[8]或滚动时域算法[5,9]求解近似最优解。

4 算例分析

4.1 算例描述和参数设置

以我国京沪高速铁路为例，依据2013年调整后的列车运行图及相关数据进行算例分析。本文算例中选择上海虹桥站和北京南站之间的42对上下行长途列车对模型进行验证，其中，速度250 km/h的Ⅱ类列车4列，速度300 km/h的Ⅰ类列车80列。该算例的详细情况，可参考文献[7]和[8]。参照这两篇文献，本文中设计的参数取值如表3所示。现场还可以根据需要修改相关参数，并不影响本文方法的实用性。

在40对Ⅰ类列车中，北京南站根据计划运行图只有18对满足动车组接续条件，而在上海虹桥站有19对车之间满足接续条件，因此，在北京南站只库存有21列Ⅰ类列车动车组情况下，有1列必须下午回送到北京南站。本算例中因缺乏实际的车型和编组数据，假设每种速度等级的列车使用相同类型的动车组、具有相同的编组。

表3 算例中相关参数取值

Tab.3 Values for parameters used in the experiments

续表3

参 数取 值 （Ⅱ类列车出发）2 （Ⅰ类列车到达）2 （Ⅱ类列车到达）1 同向列车最小发车间隔()4min 同向列车最小到达间隔()3min 同向列车同一到发线最小发到间隔（）3min 对向列车共线运行最小发到间隔（）3min 北京南站库存Ⅰ类列车动车组（）21列 北京南站库存Ⅱ类列车动车组（）2列 上海虹桥站库存Ⅰ类列车动车组（）21列 上海虹桥站库存Ⅱ类列车动车组（）2列 最大早点量30min 最大晚点量70min 1 440min 2 880min 动车组最小折返时间（）15min

除了表3中的参数取值外，假设列车在车站停站时分不小于计划运行图中的停站时分，运行时间最小值按原始图确定。由于算例中缺失京沪高速铁路原始动车组运用计划，因此，无法将调整后的列车运行图相对应的动车组运用计划和原始动车组运用计划进行比较。因此，本算例中暂不考虑目标函数中动车组偏离部分。

4.2 计算结果

在CPU为Inter(R)Core(TM) i7-4600U 2.1GHZ，内存8GB，操作系统为windows10的64位电脑上，调用CPLEX12.6对模型进行求解。

针对12种干扰情景，基于本文模型，求解的结果见表4。每种情景的三个值分别表示干扰发生时间、区间和持续时间。表4中针对13:00发生在12区间的干扰，为区分上行线路故障还是下行线路故障，在干扰情景的右上方分别标明了“up”和“down”。经计算测试发现，在干扰结束较长时间后，列车基本能恢复计划运行图运行，因此，为减小干扰对列车运行的影响范围，算例中假定列车在干扰结束6h后恢复正常 运行。

表4 考虑动车组接续的列车运行调整结果

Tab.4 Train rescheduling results considering the connection of multiple units

表4中倒数第二行为不限制干扰列车6h内恢复正常运行的结果，可见，如果给予更充足的列车恢复时间，取消列车数会减少。表4中倒数第一行为将限制求解时间延长到1h的求解结果，5min求解的结果仅比1h求解的结果差0.35%，说明5min求解结果的精度已能满足现场需要。

从表4的计算结果可知，不管干扰发生在线路的哪个部位，对于持续时间在90min及以下的干扰，本文模型均能在5min的时间内计算出最优或近似最优列车调整方案，该方案保证了动车组接续的可行性。对于持续时间小于90min的干扰，在3min内就能求得最优解，对于持续90min的干扰，在3min内求解的结果仅比5min求解的结果平均差1.53%，可见在更短的时间内（3min）求得的结果已能满足现场需要。针对设定干扰情景下的列车运行调整方案，能及时给调度员提供实时列车运行调整图，限于篇幅，仅给出干扰情景（13，12，90）down下的列车运行调整图为例，如图2所示。图中横坐标表示时间，纵坐标表示车站，其中车站从北京南站开始编号；粗线矩形表示干扰；实线和虚线分别表示Ⅰ类列车和Ⅱ类列车运行线，其中，列车运行线偏离原计划的部分用点划线表示。在图3中也采用相同的表示形式。

图2 干扰情景(13，12，90)down下考虑动车组接续的列车运行调整图

为研究动车组接续约束对列车运行调整结果的影响，基于相同干扰情景和参数值，不考虑动车组接续约束时求得的列车运行调整结果如表5所示。对于同一干扰情景（13，12，90）down，列车运行调整结果如图3所示。

对比表4和表5可知：对大多数干扰情景而言，在不考虑动车组接续约束时，干扰对列车运行的影响更小。但是，不考虑动车组接续约束时求得的列车运行图，在原来的动车组运用计划下可能不可行，如干扰情景（13，12，90）down，不考虑动车组接续约束，先调整运行图后调整动车组，导致北京南站1列出发列车无可用动车组，需取消运行或需额外增加北京南站备用动车组。如果在调整列车运行图时考虑动车组接续约束，可在适当调整始发终到列车发到时刻的情况下，保证在原动车组数量下开行所有列车。从图2和3可看出，不考虑动车组接续约束时，只有少部分受干扰直接影响的列车偏离计划运行图(图3中点划线所示)；然而，考虑动车组接续约束时，更多列车偏离计划运行图（图2中点划线所示）。

表5 不考虑动车组接续的列车运行调整结果

Tab.5 Train rescheduling results without considering the connection of multiple units

图3 干扰情景(13，12，90)down下不考虑动车组接续的列车运行调整图

5 结束语

（1）本文基于事件-活动概念构建了干扰条件下同时考虑动车组周转的列车运行调整问题网络。

（2）建立了考虑动车组周转约束的列车运行调整问题的混合整数线性规划模型。

（3）结合京沪高速铁路实际，分析了在较严重的干扰情况下，调整列车运行时考虑动车组能力约束的重要性。

（4）本文方法能够在较短时间内求解在动车组运用层面仍可行的列车运行调整方案，为现场调度员的实时调度决策提供依据。

（5）本文是从列车运行的角度出发进行调整，没有考虑旅客的行为。

[1] 范正日. 我国铁路重特大事故发生规律与特征研究[J]. 中国安全科学学报, 2018, 28(S1): 135-140.

[2] CACCHIANI V, HUISMAN D, KIDD MP, et al. An Overview of Recovery models and algorithms for real-time railway rescheduling[J]. Transportation ResearchPart B: Methodological, 2014, 63: 1 5-37.

[3] 孟令云, 杨肇夏, 李海鹰. 单线铁路区间能力失效条件下列车运行调整模型[J]. 系统工程理论与实践, 2012, 32(4): 885-894.

[4] MENG Lingyun, ZHOU Xuesong. Robust single- track train dispatching model under a dynamic and stochastic environment: a scenario-based rolling horizon solution approach[J]. Transportation Research Part B: Methodological, 2011, 45(7): 1080-1102.

[5] YANG Lixing, ZHOU Xuesong, GAO Ziyou. Rescheduling trainswith scenario-based fuzzy recovery time representationon two-way double- track railways [J]. SoftComputing, 2013, 17(4): 605- 616.

[6] 占曙光, 赵军, 彭其渊, 等. 高速铁路区间能力全失效条件下列车运行实时调整研究[J]. 铁道学报, 2015, 11(37): 1-9.

[7] ZHAN Shuguang, KROON L G, VEELENTURF L P, et al. Real-time high-speed train rescheduling in case of a complete blockade[J]. Transportation Research Part B: Methodological, 2015, 78: 182- 201.

[8] 占曙光, 赵军, 彭其渊. 高速铁路区间能力部分失效条件下列车运行实时调整研究[J]. 铁道学报, 2016, 10(38): 1-13.

[9] 王莹, 刘军, 苗建瑞. 基于运行线可调的动车组周转计划优化研究[J]. 中国铁道科学, 2012, 33(4): 112-119.

[10] VEELENTURF L P, KIDD M P, CACCHIANI V, et al. Macroscopic Railway Timetable Rescheduling Approachfor Handling Large Scale Disruptions [J]. Transportation Science, 2016, 50(3): 841-862.

Real-time High Speed Train Rescheduling Considering the Multiple Units Connecting

ZHAN Shu-guang

(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China;2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu 611756, China)

In a disrupted situation, it is critical to reschedule disrupted trains and ensure them to recover from the disruption efficiently. We consider the situation where one track in a segment of a double-track high speed railway line is blocked. A Mixed Integer Linear Programming model is formulated to solve the train rescheduling problem considering the Multiple Units connecting. The commercial software CPLEX is utilized to solve the model. Finally, Beijing-Shanghai High Speed Railway is used to test our model. The disposition timetable for each assumed disruption scenario is obtained. The results show that our approach can provide the involved railway dispatchers with a good disposition timetable in real-time. In the disposition timetable, the connecting of Multiple Units is considered as well. This is helpful to assist the dispatchers to organize trains.

high speed railway; operation disruption; real-time rescheduling;multiple unit application;mixed integer liner programming

1672-4747（2020）02-0001-10

U292.4+2

A

10.3969/j.issn.1672-4747.2020.02.001

2019-09-06

国家重点研发计划项目（2017YFB1200701）；国家自然科学基金资助项目（71701174）；中央高校基本科研业务费专项资金（2682017CX020）；河南省科技攻关计划（182102310799）

占曙光（1986—），男，湖北黄冈人，讲师（博士后），研究方向为列车运行调整，E-mail：552021114@qq.com

占曙光. 考虑动车组接续的高速铁路列车运行实时调整[J]. 交通运输工程与信息学报，2020，18（2）：1-9, 38.

（责任编辑：刘娉婷）