局部近邻标准化偏最小二乘的多模态间歇过程故障检测

李 元 ,马雨含 ,张 成 ,冯立伟

(1.沈阳化工大学信息工程学院,辽宁沈阳 110142;2.沈阳化工大学数理系,辽宁沈阳 110142)

1 引言

近年来,工业生产过程的复杂性不断提高,产品与技术不断更新换代,为了保证生产过程的安全性、可靠性以及产品质量,及时而有效的故障检测与诊断的理论的研究具有重要意义.基于数据驱动的多元统计分析的故障检测与诊断方法已成功应用于化工过程和生物过程的检测与监视,并逐渐成为工业界和学术界的研究热点[1–7].

偏最小二乘法(partial least squares,PLS)[8–10]是多元统计分析方法的一种,PLS算法利用输入对输出的解释预测作用选取特征向量,更适合应用于质量相关的故障检测.该方法已广泛应用于过程建模、监控和故障诊断等领域[11].Zhou等[12–14]提出了全潜结构投影 法(total projection to latent structures,T−PLS),将PLS的输入空间分解为4个不同的子空间来提高质量相关故障和质量无关的故障的检测精度.但偏最小二乘算法和全潜结构投影法为单模态方法,应用于多模态过程时检测效果不佳.

多模态过程[15]是重要的化工和生物生产过程,具有多中心、变量非高斯性和非线性等特点.数据的多模态性使得其故障诊断面临可靠性与准确性低等问题.Zhao 等[16–17]提出了基于主元分析(principal component analysis,PCA)算法和偏最小二乘法算法的多模型方案应用于多模态过程监控.高斯混合模型[18](Gaussian mixture model,GMM)在多模态过程监控中得到了成功的应用.但高斯混合模型的子模型个数事先未知,难以应用于复杂工业过程中.因此对多模态过程建立单一监控模型逐渐成为研究热点.马贺贺等[19]提出一种基于马氏距离局部离群因子(local outlier factor,LOF)的方法实现了单个模型对多模态过程的监控.针对多模态过程的非线性和多中心等特征,He 等[20]提出了基于k近邻(k-nearest neighbor,kNN)的故障检测方法.kNN算法[21]通过统计局部距离信息,能够有效降低非线性和多中心的影响,提高故障检测效率.但两个模态数据方差差异明显时,kNN算法的监控性能明显降低.传统的局部近邻标准化(local neighborhood standardization,LNS)方法[22]使用样本近邻集的均值和方差标准化原始数据,不同模态的数据经过处理之后能够近似满足高斯分布,解决了各个模态方差差异明显问题.但当故障位于两个模态之间时,故障样本的近邻会跨越两个模态,导致无法分离正常样本和故障样本.针对故障样本的近邻集跨模态问题,Ma等[22]提出基于局部近邻标准化策略的主元分析(local neighborhood standardization principal component analysis,LNS−PCA)方法应用于连续过程故障检测.本文针对间歇过程数据多中心、模态方差差异明显和故障样本近邻集跨模态的问题,提出一种基于局部近邻标准化偏最小二乘(local neighborhood standardization partial least squares,LNS−PLS)的多模态间歇过程故障检测方法.

注 后文将传统的近邻标准化方法用LNS表示,Ma提出的方法用MLNS表示.

2 基本算法

2.1 PLS算法

PLS算法利用潜变量提取来克服噪声和消除变量间的相关性,并通过正常生产过程数据准确捕捉质量变量与过程变量之间的关系[11–12].PLS算法具体如下:

对m个过程变量进行n次独立采样,得到输入矩阵X∈Rn×m,同时对p个质量变量进行n次独立采样得到输出矩阵Y∈Rn×p.PLS对X和Y空间的分解如下[23]:

PLS迭代算法[23]的目标函数如下:

其中:wi和ci是投影向量,ti=Xwi,ui=Y ci.由于得分矩阵T无法由W=[w1… wd]和X直接得出,定义R=[r1… rd],r1=w1,d为主元个数.对于i>1的情况有

得分矩阵T获得如下:

R,P和W有如下关系:

PLS算法对输入X分解如下:

PLS模型通常用平方预测误差(squared prediction error,SPE)和Hotelling的统计量T2来监控过程是否发生异常.T2统计量和SPE统计量的计算方法如下:

2.2 PLS方法的不足

采用PLS算法进行故障检测时,过程数据需要在检测之前进行标准化处理.目前常用的是z−score标准化方法[12,23].PLS算法的基本假设为数据具有多元高斯分布,而多模态数据z−score标准化后仍具有多模态特征,不满足该假设.设计一个数值例子来解释这种情况:模态1:x1服从N(5,0.5),x2服从N(10,0.7),y=10x1−5x2;模态2:x1服从N(20,2.5),x2服从N(10,2.2),y=10x1−5x2.在两个模态间设置一个故障点(11.5,10).图1中z−score标准化后数据仍具有多模态特征,故障样本位于两个模态之间.图2中PLS算法没有检测出故障,说明原始数据具有多模态结构时PLS算法存在不足.

图1 z−score标准化后数据散点图Fig.1 The data scatter mapping after z−score standardized

图2 PLS算法检测结果Fig.2 Fault detection results of PLS algorithm

2.3 MLNS方法

多模态数据集具有两个特征,一是各模态数据中心不重合,二是数据离散程度不同,即各模态方差不同.采用局部近邻标准化(LNS)[22]方法可以解决这两个问题.LNS标准化和z−score标准化的主要区别是LNS方法使用用每个样本局部近邻集的均值和方差,而z−score方法使用全部样本集的均值和方差.但LNS方法无法解决故障样本近邻集跨模态问题,文献[22]提出的MLNS方法解决了这一问题.两种方法具体过程如下:

找到每个样本的k近邻,并计算每个样本到其各个近邻的欧式距离.假设xi是X的一个样本,表示xi的第k个近邻,是xi和之间的欧氏距离,为样本xi的近邻集.样本xi可以按以下方法两种方法标准化:

LNS方法:

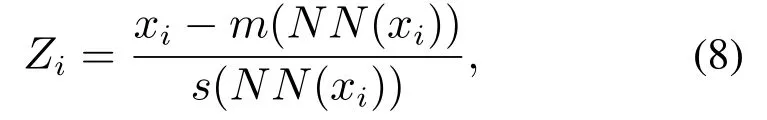
其中m(NN(xi))和s(NN(xi))分别是xi的近邻集NN(xi)的均值和方差.

MLNS方法:

其中m(NN())和s(NN())分别是xi的第一近邻的近邻集NN()的均值和方差.

LNS方法无法解决故障样本近邻集跨模态问题.采用第1.2节例子验证LNS方法和MLNS方法的效果.图3(a)中LNS方法故障样本的近邻集跨越两个模态,此时故障样本的近邻集方差较大,由式(8)可知,故障样本标准化后的数值接近正常样本的模态中心,导致故障样本和正常样本无法分离.由图3(b)可以清晰地看出故障样本湮没在正常样本之中.图3(a)中MLNS方法故障样本的第一近邻的近邻集位于一个模态.图3(c)中MLNS方法标准化后正常样本离散程度基本一致,且与故障样本完全分离.由图3(d)可知,标准化后的变量近似服从零均值的高斯分布,这是因为近邻均值总是非常接近变量值,变量x1减去其近邻均值后在零附近.

图3 LNS和MLNS方法效果Fig.3 Effect of LNS and MLNS methods

3 基于MLNS−PLS的多模 态 间歇过 程故障检测

本文采用统计模量[25–26]方法处理间歇过程数据.统计模量方法是用统计特征矩阵重新定义原始间歇过程数据,一般所用的统计特征为均值和方差.PLS算法应用于多模态间歇过程故障检测时效果不佳.LNS方法解决了这一问题,但仍存在缺陷,当故障样本的近邻集跨模态时,该方法无法分离正常样本和故障样本.本文使用MLNS方法处理数据,提出了一种基于局部近邻标准化偏最小二乘(MLNS−PLS)方法改进PLS算法处理多模态间歇过程数据的不足.MLNS标准化后变量近似服从零均值的高斯分布,符合PLS算法基本假设.基于MLNS−PLS方法的故障检测包括离线建模和在线检测两部分,具体步骤如下:

离线建模:

1)在训练集X中寻找每个样本xi的k个局部近邻集NN(xi),在训练集Y中寻找每个样本yi的k个局部近邻集NN(yi);

2)用xi的第一近邻的近邻集的均值m(NN())和方差s(NN())来标准化xi,同理得到标准化后的yi;

3)在MLNS处理后的数据集上,利用式(3)−(4)确定PLS的得分矩阵T,利用式(6)计算残差矩阵;

4)计算每个样本的SPE统计量和T2统计量及控制限.

在线检测:

1)对于待检测样本xj和yj,分别在训练集X和Y中找到xj和yj的第一近邻和;

2)用的近邻集的均值m(NN()和方差s(NN())来标准化xj,同理得到标准化后的yj;

3)利用负载矩阵将MLNS方法标准化后的数据投影到PLS的主元空间和残差空间;

4)计算待检测样本xj和yj的SPE统计量和T2统计量,并与控制限比较确定检测结果.

4 实验应用研究

4.1 数值实例的分析与实验

使用多模态数值实例分析MLNS−PLS方法的检测性能,同时与PLS算法、kNN算法和LNS−PLS方法的结果进行对比分析.所用模型如下:

其中:x1,x2,x3是输入X的3个变量,y1,y2是输出Y的两个变量.取500组训练数据,两个模态各250组;取10组校验数据,两个模态各5组;在3个变量上设置偏移,产生5个故障点f1(−3,−2,−3),f2(0,0.5,0.5),f3(0.7,0.1,0.3),f4(0.5,1.2,1.3),f5(1,0.5,1).

检测过程中主元数为2,kNN算法的近邻数为3,LNS−PLS方法和MLNS−PLS方法的近邻数为10.仿真结果如图4−9所示.图中黑色实线是置信度为99%的控制限.原始数据所有变量分布见图4,图中两个模态数据方差差异明显,模态1数据分布密集,模态2数据分布较为稀疏,故障1靠近模态2,故障2和故障3在两个模态之间,故障4和故障5靠近模态1.

图4 原始数据散点图Fig.4 Original data scatter mapping

图5 数据散点图Fig.5 Data scatter mapping

图6 z−score−PLS算法检测结果Fig.6 Fault detection result of z−score−PLS algorithm

图7 kNN算法检测结果Fig.7 Fault detection result of kNN algorithm

图8 LNS−PLS算法检测结果Fig.8 Fault detection result of LNS−PLS algorithm

图9 MLNS−PLS算法检测结果Fig.9 Fault detection result of MLNS−PLS algorithm

图6中PLS算法未检测出故障,且正常样本的统计量差异明显.图7中kNN算法检测出故障1和故障2,当两个模态疏密程度不一致时,两个模态样本的D2统计量差异明显,此时控制限由稀疏模态决定,故障4和故障5为靠近密集模态的微弱故障,无法被检测.

图8中LNS−PLS方法未检测出故障2和故障3.因为故障2和故障3的近邻集跨越两个模态,以故障2为例,它的前两个近邻属于第二模态,而第三近邻属于第1模态,使得故障2的近邻集方差较大,由式(8)可知,标准化后的故障2靠近正常样本中心,导致故障2和正常样本无法分离.从图5(a)中可以看出LNS方法标准化后故障2和故障3位于正常样本中心周围.

图5(b)清楚的表明MLNS标准化消除了数据的模态结构信息,故障样本和正常样本完全分离.因此图9中,综合T2和SPE两个指标,MLNS−PLS方法检测出所有故障.

4.2 青霉素过程的故障检测

青霉素生产过程是一个典型的非线性、多模态间歇生产过程.其发酵过程可分3个阶段:菌体快速生长阶段、菌体合成青霉素阶段和菌体自溶阶段.本文基于Pensim仿真平台[27–28],验证基于MLNS−PLS故障检测方法的有效性.青霉素发酵过程流程如图10所示.

Pensim仿真平台有5个输入变量可以控制发酵过程参数变化,9个过程变量是菌体合成及生长中产生的,5个质量变量影响青霉素的产量.本文选取7个过程变量作为输入和5个质量变量作为输出,变量选取[8]见表1.本文使用Pensim仿真平台生成数据,仿真时间设定为400 h,采样时间设定为1 h.在正常工况下生成两个模态数据:模态1初始CO2浓度设定为0.5,通过调整初始变量值生产50个批次,为稀疏模态;模态2初始CO2浓度设定为1,通过微调初始变量值生产75个批次,为密集模态.从两个模态中各随机选取5个批次作为校验样本,剩余115个批次作为训练样本.图11中可看出正常批次的CO2浓度分为两个模态.

图10 青霉素发酵过程流程图Fig.10 Flow chart of penicillin fermentation process

表1 青霉素发酵过程变量选取Table 1 Variable selection of penicillin fermentation process

图11 正常样本的CO2浓度Fig.11 CO2 concentration of normal samples

Pensim仿真平台能对前3个变量(通气率、搅拌功率和底物流速率)引入故障,故障类型有阶跃和斜坡两种,并可进一步设定两种故障的幅度、引入时间和终止时间.为了测试方法的有效性,本文在实验中生产12个故障批次,12个故障批次的故障类型及程度见表2.

表2 青霉素发酵过程中设置的12个批次故障Table 2 Twelve faults of penicillin fermentation process

青霉素发酵过程数据是间歇过程三维数据矩阵,本文采用统计模量方法将数据处理成二维矩阵.使用PLS算法、kNN算法、LNS−PLS方法和MLNS−PLS方法对青霉素发酵过程进行仿真实验和对比分析.实验中PLS算法、LNS−PLS方法和MLNS−PLS方法的主元数取3.kNN 算法的近邻数取10,标准化方法为z−score方法.LNS−PLS方法和MLNS−PLS方法的近邻数取15.实验结果见图12−16和表3.

图12 数据散点图Fig.12 Data scatter mapping

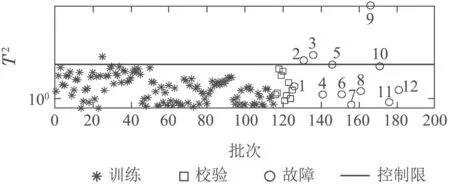
图13 z−score−PLS算法检测结果Fig.13 Fault detection result of z−score−PLS algorithm

图14 kNN算法检测结果Fig.14 Fault detection result of kNN algorithm

图15 LNS−PLS算法检测结果Fig.15 Fault detection result of LNS−PLS algorithm

图16 MLNS−PLS算法检测结果Fig.16 Fault detection result of MLNS−PLS algorithm

表3 12个故障批次的检测结果Table 3 Fault detection results of 12 batches

图12中正常样本分为两个模态,并且两个模态的数据离散程度不同.图13中PLS算法的T2和SPE共检测出6 个故障,多模态数据不服从多元高斯分布,故PLS算法检测效果不佳.图14中kNN 算法未检测出故障7、故障11和故障12.因为当两个模态数据离散程度不同时,kNN 算法的控制限由方差大的第1模态决定,故障11为靠近密集模态的微弱故障(见图12),它的统计量D2在两个模态正常样本的统计量之间,无法被检测.故障7和故障12同理.图15中LNS−PLS方法未检出故障6、故障7和故障8,因为这3个故障样本的近邻集跨越两个模态.以故障7为例,其第1近邻和第2近邻分别是第9号和27号样本都属于第1模态,而其第3近邻为第104号样本属于第2模态.此时故障7的近邻集方差较大,由式(8)可知,标准化后的故障7接近正常样本的模态中心,导致故障7和正常样本无法分离,故障6和故障8同理.图16中MLNS−PLS方法检测出全部故障,且两个模态正常样本的统计量差异不大.综上所述,MLNS−PLS方法解决了两个模态数据方差差异明显和故障样本近邻集跨模态的问题.

5 结论

针对PLS算法无法有效应用于多模态间歇过程故障检测的问题,本文提出一种局部近邻标准化偏最小二乘(MLNS−PLS)方法.先利用MLNS方法处理统计模量后的数据,避免了故障样本的近邻集跨模态的情况;再利用PLS算法进行故障检测,改善了PLS对多模态间歇过程数据的检测效果.将MLNS−PLS方法应用于青霉素发酵过程的故障检测,实验结果表明,MLNS−PLS方法能保证较好的检测效果,该方法可以应用到其他工业和生物领域的多模态间歇过程的故障检测中.