基于新型人工蜂群算法的分布式不相关并行机调度

刘美瑶,雷德明

(武汉理工大学自动化学院,湖北武汉 430070)

1 引言

随着经济和贸易全球化的不断发展,制造业从集中式制造转变为分布式制造,分布式制造已成为常见制造模式,相应的生产调度问题也变成分布式调度问题[1–2],分布式调度比传统的调度更复杂,在快速响应市场需求方面优势更大.并行机调度是实际制造过程中一类典型的调度问题,它在分布式环境下扩展为分布式并行机调度问题(distributed parallel machines scheduling problem,DPMSP),DPMSP在实际分布式制造过程应用广泛[3–4],如包括Polyvinyl Chloride管[4]在内的化学品生产,其研究具有重要的理论和现实意义.

近年来,DPMSP研究取得了一些进展[4–10].Lei等[4]设计了一种带记忆的帝国竞争算法.Behnamian等分别应用遗传算法(genetic algorithm,GA),变邻域搜索和双阶段算法等解决了多种类型的DPMSP[8–10].只是现有研究主要关注了各工厂机器数量和机器加工能力等完全一样的同构工厂DPMSP,较少关注异构工厂环境下的DPMSP,且并行机多为同速并行机,很少考虑不相关并行机.由于不相关并行机在制造过程中普遍存在[4],且实际多工厂往往为异构工厂,导致相应的调度问题更复杂,求解困难更大,因此,有必要研究异构工厂下的分布式不相关并行机调度问题(distributed unrelated parallel machines scheduling problem,DUPMSP).

调度问题建模时,通常假设所有机器在调度过程中一直可用,而实际制造过程中机器难免会因为老化、违规操作、零件磨损、管理不善和外界因素等需要进行预防性维修(preventive maintenance,PM)[11–12].PM的时间窗固定或动态变化.动态时间窗更灵活,能有效地减少机器空闲时间,从而大幅提高机器的利用率,因此,具有动态时间窗的PM受到广泛关注.目前,考虑PM的调度问题有一些进展[13–24],不过,以上研究主要在单工厂环境下进行,分布式环境下考虑PM 的调度问题,尤其是具有PM的DUPMSP,未引起研究者的关注.

人工蜂群算法(artificial bee colony,ABC)[25]由土耳其学者Karaboga于2005年提出,它具有控制参数少、操作简单、易于实现等优点.目前ABC已成功解决了单工厂环境下的多种调度问题[26–30],不过,ABC在分布式调度方面的应用研究才刚刚起步[31–32].由于ABC的显著特点及其在求解调度问题方面的优势,本文探讨ABC在DUPMSP方面的应用可能.

针对考虑PM的DUPMSP,提出一种新型ABC以最小化最大完成时间.该算法将整个种群划分成4部分,其中跟随蜂群划分为3部分,跟随蜂有自己的蜜源,引领蜂、跟随蜂和侦查蜂搜索策略各异,并利用优化数据更新整个种群.通过大量的仿真实验验证了新型ABC在求解所研究问题方面的有效性和优势.

2 问题描述

DUPMSP描述如下:假设n个工件分配在F个工厂内加工,工厂f内有mf台不相关并行机Msf+1,…,Msf+mf,其 中总共W台机器.每个工件只有一道加工工序,只需在任一台机器上加工一次,工件Ji在机器Mk上的加工时间为pik.

每台机器都有多个PM时间窗,机器Mk必须在动态时间窗[ukl,vkl]内进行PM,维护时长为wkl,其中(vkl −ukl)wkl,l=1,2,….机器Mk第l次PM的起始时间,结束时间分别为Skl和Ekl,Sklukl且Eklvkl,Ekl=Skl+wkl.

还需满足以下约束:所有机器在零时刻均可加工工件,工件在加工过程中一经打断需重新开始,一台机器同一时刻只能加工一个工件,每个工件在同一时刻只能在一台机器上加工等.

DUPMSP包括3个子问题[9]:1)工厂分配,确定所有工件在各工厂之间的分配;2)机器分配,在每个工厂为工件确定合适的机器;3)调度,确定各机器上工件的加工顺序.两个分配子问题之间具有非常紧密的联系,工厂分配决定了机器分配的内容,而工厂分配的效果取决于机器分配和调度.若扩展机器分配,在所有工厂为工件确定合适的机器,一旦机器分配确定,就可通过统计各工厂内的机器所分配的工件,而确定工厂分配,这样可将两个分配问题集成为扩展的机器分配问题.

问题的目标为在满足所有约束条件下最小化最大完成时间.

其中:Ci表示工件Ji的完成时间,Cmax为最大完成时间.

表1给出了DUPMSP的一个实例的加工时间,有2个工厂和30个工件,其中工厂1有2台不相关并行机,工厂2有3台不相关并行机,对应的一种调度方案如图1所示.

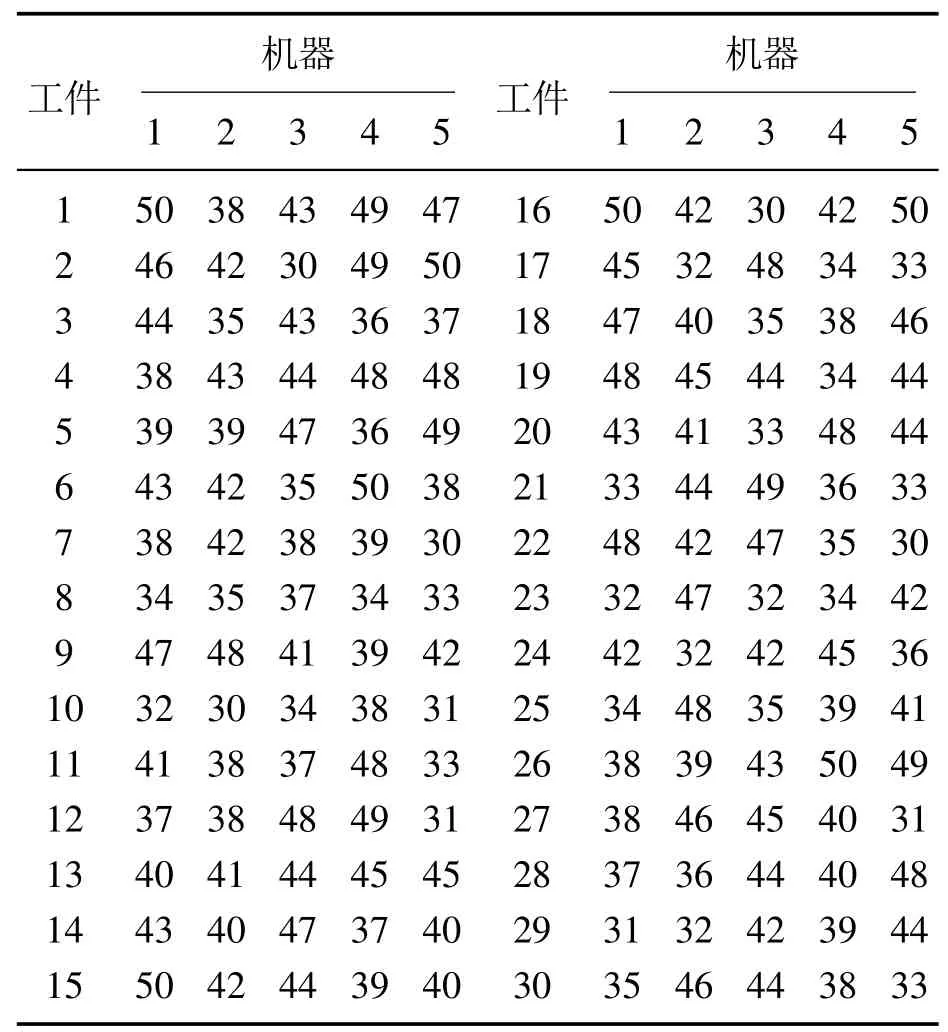
表1 加工时间Table 1 Processing time

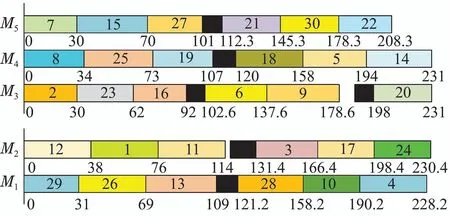
图1 实例的甘特图Fig.1 The Gantt chart of the example

3 基于新型ABC的DUPMSP

3.1 初始化

由于工厂分配和机器分配集成为扩展的分配问题,整个问题由扩展的机器分配和调度组成,为此,采用双串编码方式.对于具有n个工件和W台机器的问题,其解由机器分配串和调度串组成,其中机器分配串[Mh1Mh2… Mhi … Mhn]中,Mhi为加工Ji的机器;调度串[q1q2… qi … qn]中,qi为工件Ji对应的实数.

调度串为实数串,假设工件Ji,Ji+1,…,Jj在同一台机器上加工,即Mhi=Mhi+1=…=Mhj,则这些工件的加工顺序由ql的升序决定,其中l∈[i,j].

解码过程如下:对每台机器,根据第1个串确定所分配的所有工件并按这些工件对应的ql的升序排列,确定该机器上所有工件的加工顺序.假设机器Mk上工件的加工顺序为Jk1,Jk2,…,Jkg,对于机器的第l次PM,根据如下3种情况之一安排工件加工:

1)如果αk+pkhkukl,则Ckh=αk+pkhk,αk=Ckh;

2)如果αk+pkhk >ukl且αk+pkhk+wklvkl,则Skl=αk+pkhk,αk=Skl+wkl,l=l+1;

3)如果αk+pkhk+wkl >vkl,则Skl=ukl,αk=Skl+wkl,l=l+1.

其中αk表示Mk最早空闲的时间.

如上所示,部分工件的开始时间和完成时间与PM的开始时间密切相关,增加了解码过程的复杂性.如果不考虑PM且目标函数仅为最大完成时间,则无须优化调度子问题;随着PM的加入,需要考虑调度串的优化,主要在于PM的开始时间会随工件的加工顺序的变化而改变.

图2给出了表1实例的一种可能解,工件J1,J3,J11,J12,J17,J24分配给M2,这些工件对应的qi的升序排列为0.31,0.33,0.42,0.49,0.68,0.86,故先加工J12,再加工J1,依此类推,对应的甘特图如图1所示.

图2 实例的一个解Fig.2 A solution of the example

如图1所示,解码过程所得到的调度方案是可行的.实际上,机器分配串保证了每个工件不能同时分配到两台机器上,从而保证一个工件无法同时在两台机器上加工;而每台机器上工件都按调度串决定的顺序依次加工,不可能在同一时间同时加工两个工件,也就是编码串已保证每个解都是可行的,无不可行解存在.

随机产生初始种群P,并根据如下过程将种群划分为1个引领蜂群EB 和3 个跟随蜂群OB1,OB2,OB3:将初始种群的N个解根据Cmax非降序排列,前β1×N个解作为引领蜂的蜜源,剩余解分配给跟随蜂作为蜜源,并且所有跟随蜂细分为3类,在剩余解中,前β2×N个解组成OB1,作为第1类跟随蜂的蜜源,第2类跟随蜂群OB2的蜜源为剩下的解中Cmax最小的β3×N个解,剩余的β4×N个解分配给第3类跟随蜂群,其中β1+β2+β3+β4=1.基于大量实验将参数β1,β2,β3,β4分别设置为0.4,0.1,0.25,0.25.

划分种群后,不同蜂群采用不同的搜索方式,这样可以运用多种策略产生新解,保持种群的多样性,并高效利用质量较好的解.

3.2 引领蜂阶段

通常,ABC不能直接用于离散型问题的求解,为此,在两个解之间采用两点交叉进行全局搜索.两点交叉可作用于两个串,且作用过程类似,主要包括随机确定两个位置,然后将一个解位于两个位置间的基因用另一个解对应位置上的基因替代.局部搜索包括4个邻域结构N1,N2,N3,N4,由于调度串对整个解的影响有一定限制,未设计调度串的邻域结构.

邻域结构N1描述如下:先确定完成时间最大的机器Ml并任选一台机器Mr,从Ml上随机选择一个工件转移到Mr上.N2过程如下:确定完成时间最大的机器Ml以及Ml上加工时间最大的工件Jh,任选一台机器Mr并确定其上加工时间最大的工件Jg,在机器分配串中互换Jh,Jg的位置.N3的过程与N2类似,只是两台机器是随机选择的,而N4则将随机选择的两台机器上随机选择的两个工件互换.

引领蜂群的搜索过程如下:对于解x∈EB,

1)如果随机数s<δ1,则随机选择y∈EB,对解x,y执行机器分配串的两点交叉,产生新解z1,若z1优于x,则z1替代x且Ω=Ω ∪{x}.否则对解x,y执行调度串的两点交叉,得到z2,Ω=Ω ∪{z2}并更新x.

2)如果随机数s<ε1,则g=1,重复执行如下过程R次:产生邻域解z∈Ng(x),Ω=Ω ∪{z},并用z更新x;否则g=g+1 并令g=1 若g=5.

解的更新规则遵循贪婪选择策略即若新解优于x,则新解替代x.集合Ω用来保留算法搜索过程产生的解.

上述过程中,参数δ1,ε1为实数,通过实验分别设置为0.7,0.1.

3.3 跟随蜂阶段

通常,跟随蜂本身并无蜜源,而是根据概率选择一个引领蜂的蜜源,且由于跟随蜂只是利用引领蜂群的蜜源进行搜索,往往采用和引领蜂同样的搜索方式.本文为跟随蜂分配了蜜源,并应用几种彼此各异的搜索策略产生新解.

3种跟随蜂群的具体搜索过程如下:

1)对于每个解x∈OB1.

a)如果随机数s<δ2,则对解x和EB中的最优解x∗执行第3.2节中x,y之间的交叉过程;

b)如果随机数s<ε2,则对解x执行第3.2节所述的多邻域搜索.

2)对于每个解x∈OB2.

a)如果tT,当随机数s<δ3时,对解x和EB中的最优解x∗执行第3.2节中x,y之间的交叉过程;

b)否则,当s<ε3时,随机选择y∈EB,g=1,执行如下过程R次:产生邻域解z∈Ng(y),若z优于x,则z替代x,Ω=Ω ∪{x};否则g=g+1,令g=1若g=5.

3)对于每个解x∈OB3.

如果随机数s<ε4,则随机选择y∈EB,执行和x∈OB2第2种情况下同样的多邻域搜索.

上述过程中,参数δ2,δ3,ε2,ε3,ε4为实数,通过实验分别设置为0.9,0.9,0.1,0.6,0.5.t,T分别表示实际的目标函数估计次数和给定目标函数估计次数,基于大量实验设置T=2×104.

如上所述,OB1的搜索过程和EB中的解搜索过程类似,只是全局搜索的对象不一样,其他两个跟随蜂群中的解的搜索过程和方式也各异.通过多种不同途径产生新解,有助于避免算法搜索停滞,增加种群多样性.

3.4 算法描述

新型ABC的具体步骤描述如下:

1)初始化.随机产生初始种群P,令t=1.

2)如果tmax_it,则

a)令集合Ω为空,将种群P划分为EB,OB1,OB2,OB3,Ω=Ω ∪EB;

b)引领蜂阶段;

c)跟随蜂阶段;

d)侦查蜂阶段;

e)对集合Ω中的解非降序排序,排名靠前的N个解组成新种群.

3)输出最终结果.

其中max_it表示最大目标函数估计次数,在搜索过程中,每产生一个解,t自动增1.

侦查蜂阶段针对OB3中的最差解xw,如果随机数s<θ,则随机选择一个解x∈EB,然后,对x执行跟随蜂搜索过程第2步的第2种情况下的多邻域搜索过程,如果所得到的最好解优于xw则用前者更新后者,其中参数θ为实数，通过实验设置为0.4.

由于OB3中的最差解往往是种群内的最差解,故直接从OB3中选择.和常规侦查蜂阶段不一样,本文未采用随机搜索,而是从EB中随机确定一个解进行多邻域搜索,这样可大概率地保证最差解得到更新和改进.

集合Ω用来存储ABC搜索过程产生的优化数据,每一次循环中,Ω都会清空,搜索开始后,先将EB中的解加入到Ω中,EB 搜索过程中两点交叉产生的新解,无论是否优于x,都放入Ω中,多邻域搜索产生的解也直接放入Ω中,跟随蜂群产生的新解处理方式类似,这样引领蜂群和跟随蜂群一次搜索至少产生N个解,再加上EB中的解,使得集合Ω的解至少N个,且搜索过程得到的好解都保留在集合Ω中,精英解也保留在Ω中,为此,将Ω中N个Cmax最小的解直接替换当前种群内所有解.

新型ABC搜索过程中,PM的处理始终在解码时进行,这样无需在两点交叉和邻域搜索时考虑PM的处理,简化了搜索算子的设计;而且,两点交叉和邻域搜索不改变两个编码串的可行性,不会产生不可行解,其流程图如图3所示,时间复杂度为O(N ×G),其中G为步骤2循环的次数.

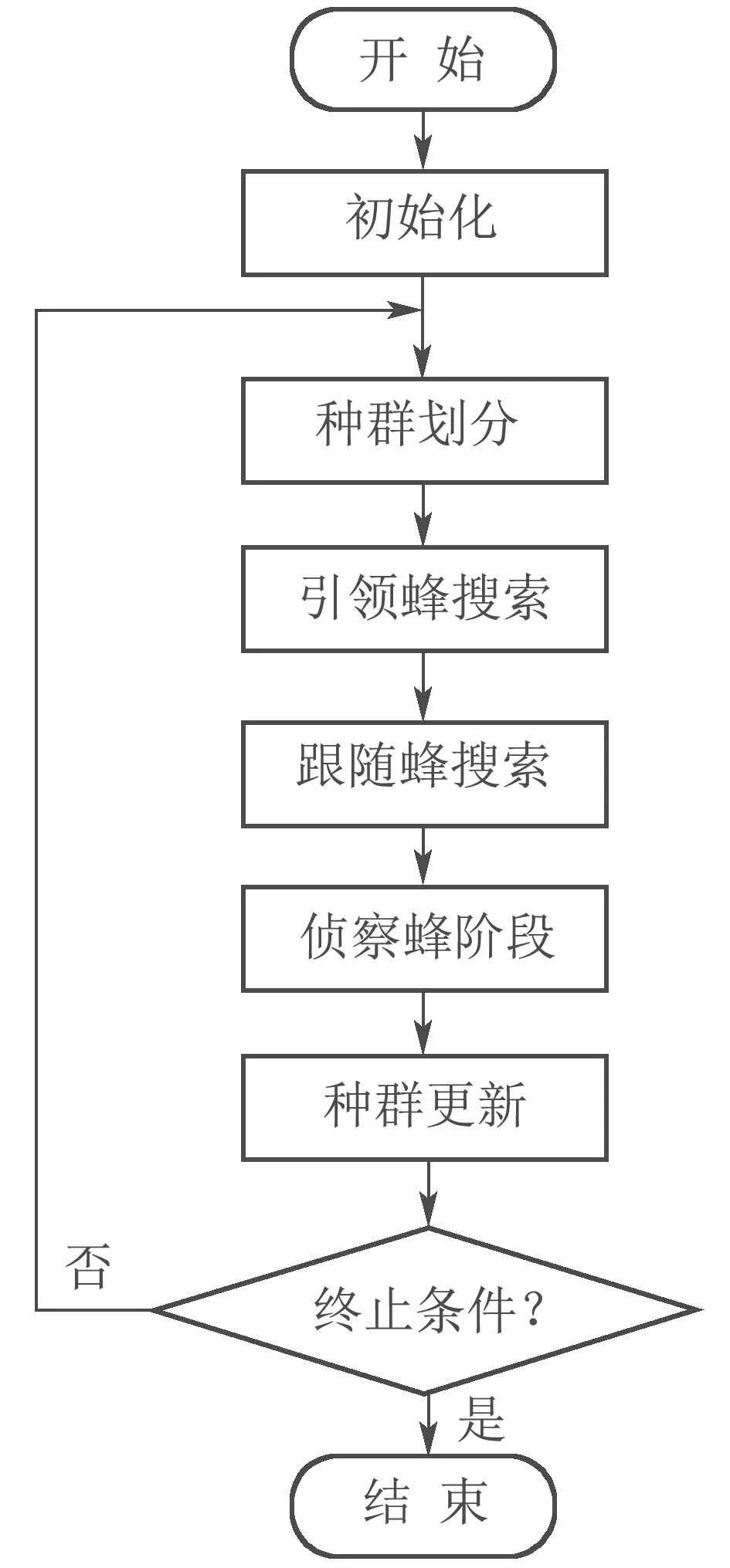
图3 新型ABC流程图Fig.3 Flow chart of new ABC

新型ABC具有如下特点:将种群划分成4部分,第1部分是由引领蜂的蜜源组成的集合,其余3部分由跟随蜂的解组成,不同部分采用不同的搜索策略,侦查蜂阶段用邻域搜索的解替代OB3中最差解,并利用Ω中保留的优化数据直接更新整个种群.这些特点有助于ABC保持种群多样性,避免陷入局部最优.

4 计算实验

为了验证新型ABC在求解考虑PM的DUPMSP的有效性,进行了大量的计算实验,所有测试实验均通过Microsoft visual C++2017编程实现,在4.0 G RAM 2.70 GHz CPU 环境下运行.

4.1 测试实例与对比算法

本文选用64个实例测试所提算法性能,表2描述了实例的基本信息,其中具有n=60,70,80的16个实例属于中规模实例,其余为大规模实例.pik在区间[30,50]内随机产生,对于每台机器Mk,相关数据为

其中rk(l−1)表示第(l −1)次PM结束时间.

表2 实例信息Table 2 Information on instances

目前,DPMSP相关研究进展不大,关于DUPMSP的研究更少,故难以找到能直接应用于DUPSMP求解的对比算法.Behnamian和Ghomi[9]提出了一种基于矩阵编码的GA来求解DPMSP.在GA中,随机生成初始种群,通过复杂的交叉操作和特殊的变异产生新解,适应度最高的个体自动复制到下一代,并采用局部搜索来提高搜索能力.该算法无须任何修改就可直接用来求解带有PM的DUPMSP,因此选择GA作为对比算法.

Mir等[33]针对不相关并行机调度问题提出了混合粒子群遗传算法(hybrid particle swarm optimization and genetic algorithm,HPSOGA),在解码过程中加入本文描述的关于PM的处理过程后,该算法可直接应用于DUPMSP的优化,故选择它作为一种对比算法.

模拟退火算法(simulated annealing,SA)具有避免陷入局部最优的特点,已被广泛应用于求解多种组合优化问题.Yeh等[34]研究了具有学习效应的并行机调度问题,将SA应用于该问题的求解并获得了良好的效果.只需修改该算法的解码部分,便可直接用于求解DUPMSP.为验证本文所提算法性能,故选择该局部搜索算法作为对比算法.

新型ABC的主要策略是种群划分和不同蜂群采用不同的搜索方式.为验证这些策略的有效性,构建了新型ABC算法的变体ABC1,该算法没有种群划分,跟随蜂阶段中,跟随蜂随机选择一只引领蜂,并采用引领蜂相同的方式搜索.

所有算法对每个实例随机运行20次,指标MIN和MAX分别表示最优解和最差解,AVG为20次运行结果的平均值.图4描述了两个实例的收敛曲线.

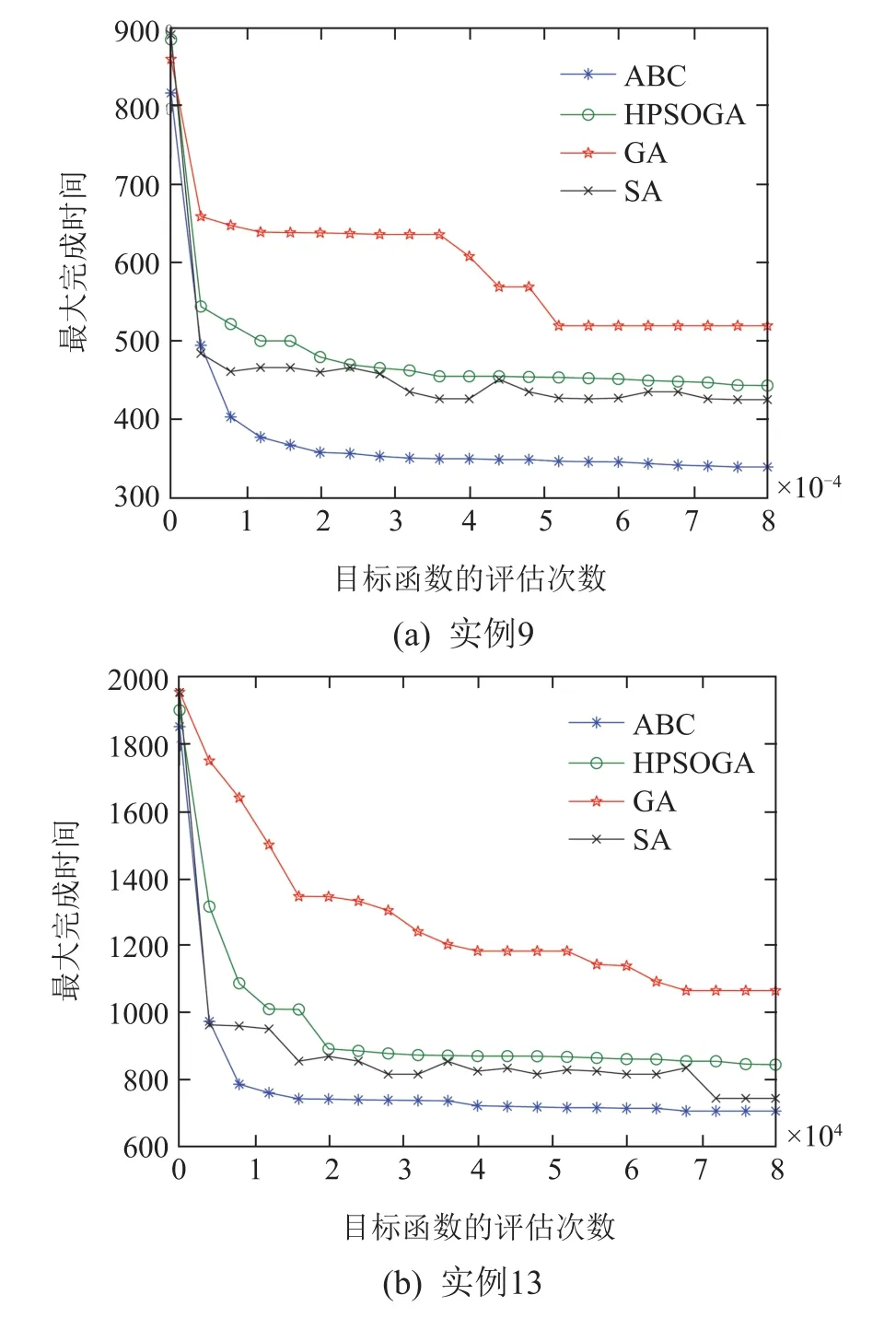
图4 收敛曲线Fig.4 Convergence curves

新型ABC主要参数包括maxit,N,β1和R,通过对所有实例进行参数测试实验,可发现,当N=100,R=4,max_it=8×104和β1=0.4时,算法性能最好,故采用上述参数设置.HPSOGA、GA和SA除终止条件之外的所有参数直接来自文献[9]和文献[33–34],所有算法采用和新型ABC相同的终止条件,实验结果如表3–5所示,表6描述了算法的计算时间,时间单位为s.

4.2 实验结果与比较

如表3–5所示,和ABC1相比,新型ABC关于64个实例中的56个取得了更优的MIN,关于56个实例所获得的MAX更小或者等于ABC1的MAX,关于62个实例取得了更小的AVG,这表明了新型ABC明显优于ABC1,从而验证了种群划分和不同部分采用不同搜索策略改进算法性能的有效性.将种群划分为1个引领蜂群和3个跟随蜂群,蜂群的搜索策略各异,这样有助于避免ABC陷入局部最优,提高搜索效率.配对样本均值t检验的结果如表7所示,t-test(A,B)表示一次配对t-test,用来判断算法A是否给出了优于B的样本均值,假设显著水平为0.05,若p-value<0.05,说明算法A优于算法B.

如表3–6 所示,和3 个对比算法HPSOGA、GA与SA相比,新型ABC在较短的计算时间内所获得的搜索性能明显占优,其中关于指标MIN,新型ABC关于55个实例的结果比HPSOGA最少低70,关于58个实例比GA最少低150,关于55个实例的结果比SA最少低75,对于其他两个指标MAX和AVG也可以得到类似结论,而且新型ABC关于所有测试实验的计算时间也明显优于HPSOGA和GA.表7所示的结果也显示,新型ABC和3种对比算法之间的性能差异是显著的.

表3 5种算法关于指标MIN的计算结果Table 3 Computational results of five algorithms on metric MIN

表4 5种算法关于指标MAX的计算结果Table 4 Computational results of five algorithms on metric MAX

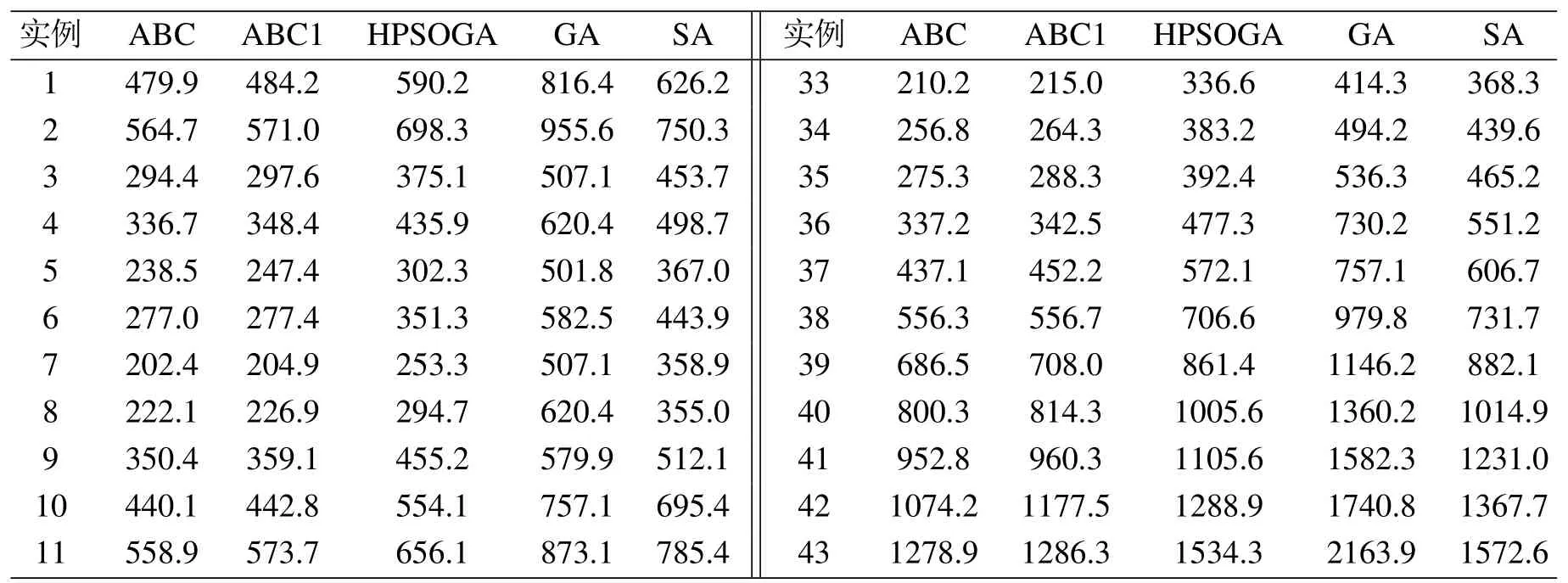
表5 5种算法关于指标AVG的计算结果Table 5 Computational results of five algorithms on metric AVG

表6 ABC,HPSOGA,GA和SA的计算时间Table 6 Computational times of ABC,HPSOGA,GA and SA

和GA相比,新型ABC的编码方式更简单,局部搜索和全局搜索之间的平衡更好;和HPSOGA相比,新型ABC将种群划分为多个蜂群,且不同蜂群的搜索策略各异,这样有利于提高搜索效率,避免陷入局部最优;和SA相比,新型ABC除了局部搜索还运用了全局搜索,种群内不同解之间进行信息交流,有助于找到全局最优解.新型ABC还采取和传统ABC不同的跟随蜂跟随方式,且跟随蜂自身也有蜜源,并利用优化过程中产生的数据来更新种群,构造新种群,这样策略能有效地实现探索和利用间的良好平衡,对获得高质量的优化结果有利,从而表明,新型ABC是解决具有PM的DUPMSP具有较强竞争力的方法.

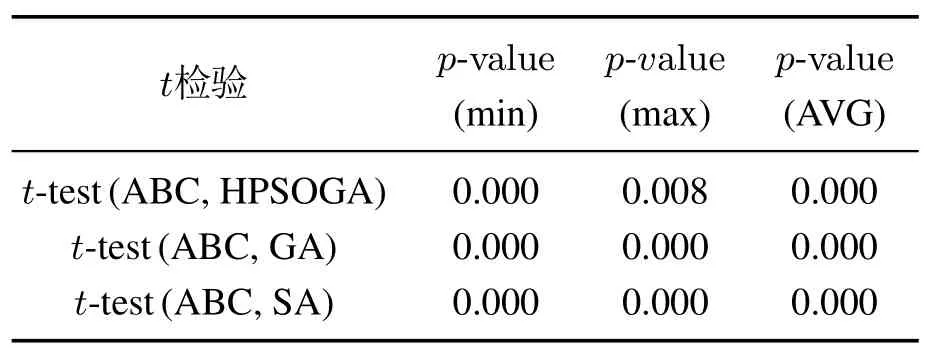
表7 配对样本t检验Table 7 Results of paired sample t-test

5 结论

在分布式环境下的调度问题中考虑机器可用约束如PM更有意义和价值.针对考虑PM的DUPMSP,提出一种新型ABC以最小化最大完成时间.该算法采用全新的种群划分策略,不同蜂群采用不同的搜索策略,跟随蜂具有自己的蜜源并采取新的跟随方式,采用新策略完成侦查蜂搜索和更新整个种群.运用大量的实例对算法性能进行测试,实验结果验证了新型ABC的有效性和搜索优势.

分布式调度是目前调度研究的焦点,但现有研究很少讨论实际加工约束,未来将深入研究具有随机故障,零等待和不确定加工条件等的分布式调度问题及其相应的高效智能优化算法.