基于预测窗的轮式移动机器人最优避障避碰算法

刘中常 王明杰 郭 戈

(1.大连海事大学船舶电气工程学院,辽宁大连 116026;2.东北大学流程工业综合自动化国家重点实验室,辽宁沈阳 110004)

1 引言

具备自主感知、决策和执行能力的移动机器人之间的相互避碰以及躲避(静止或移动的)障碍物是机器人研究领域的一个重要问题,其基本目标是控制移动机器人在有障碍物和其他移动机器人的环境中实现无碰撞运动并到达规定的目的点,这在仓储物流、智能交通、区域搜索覆盖等任务中有着广泛的应用前景.

常用的避障和避碰算法包括基于实时状态的势场函数法[1]和基于预测的动态窗法[2]、模型预测法[3]、障碍函数法[4]和速度障碍法[5]等及其混合方法[6].基于实时状态的势场函数法在结构上比较简单,因而得到了广泛应用,但是其容易陷于局部极值而使得机器人避碰或避障失败或由于障碍物的存在而无法到达目标点.基于预测的方法可以根据当前时刻的状态来估计未来会发生碰撞的情况,因而可以通过优化的方法求得机器人当前时刻的最优避碰避障策略.大多数基于预测的算法[7–8]是针对无自主决策能力的障碍物来设计的,移动机器人根据预测的障碍物未来的运动轨迹来进行避碰控制.例如,文献[5]中通过构造速度障碍(velocity obstacle,VO)的方法,把移动机器人与障碍物所有可能会发生碰撞的相对速度定义成一个速度障碍集合,通过在速度障碍集合之外选取最优的避障速度来达到避障的目的.当障碍物是具有主动避障能力的移动机器人时,简单地把其看作一般被动障碍物来躲避就很可能会导致运动的振荡[9–10],甚至可能发生碰撞.因此,文献[10]中,在文献[5]的基础上提出了协作式的速度障碍(reciprocal velocity obstacle,RVO),将避障责任平均分配给每个移动机器人,实现了多移动机器人的协同避碰,但在机器人的数量较多时仍会导致运动的振荡.为了弥补这个不足,文献[11]继续进行改进,提出了最优相互避碰算法(optimal reciprocal collision avoidance,ORCA),将无碰撞的安全速度区域用半平面来表示,然后通过优化算法求解最优的无碰行驶速度.由于这一算法能保证避障和相互避碰、具有最优性且易于计算,因而得到了广泛的应用.例如,应用于多机器人的区域覆盖问题[12];最近,本文作者在文献[13]中采用两个预测周期来躲避高速移动的障碍物.但该算法只适用于具有完整约束动态的机器人,对于非完整约束机器人,已有文献中的做法是将机器人模型近似转换成完整约束机器人模型.例如,文献[14]把差分驱动机器人近似成一种完整约束机器人,再应用ORCA算法计算出最优的避碰速度并转换成左右轮的驱动速度;文献[15]研究了后轮转向固定而通过前轮进行转向的车式机器人,根据其跟踪完整约束轨迹的最大误差来增大有效避碰半径,从而保证其能够无碰行驶;文献[16]将文献[15]中的方法进行了推广,研究了更一般化的具有非完整约束的机器人的避碰问题.

除了上述问题,文献[10–11]中基于速度障碍的避碰算法计算出的控制量是机器人的速度,并假设求得的新速度瞬时可达,导致机器人的运动轨迹和速度是分段的,不够平滑,且不适用于具有加速度约束的机器人.另外,这些算法假设障碍物在预测窗内速度保持初始值不变,这并不利于躲避速度变化剧烈的障碍物.对此,文献[17]提出了基于加速度—速度障碍(acceleration velocity obstacle,AVO)的相互避碰算法,采用比例控制的方法使机器人在预测窗内加速到期望速度.文献[18]中进一步采用机器人位置的多阶导数进行比例反馈控制来对期望速度进行跟踪控制.文献[19]采用LQR方法来设计速度跟踪控制器.文献[20]中提出了一种基于控制障碍(control obstacle,CO)的避碰算法,对机器人用于避碰的控制增量进行规划,从而将文献[17]中的算法进行了统一化处理,且能适用于不同类型的移动机器人之间的相互避碰.上述这些方法虽然可以在一定程度上平滑机器人的运动轨迹,但其本质上都是对期望速度的跟踪控制,不但会有跟踪误差,而且可能导致机器人的加速度变化剧烈,从而使得执行机构产生较大磨损.为此,文献[21]将ORCA算法和模型预测控制相结合,对机器人的加速度进行优化控制,取得了良好的效果,但也只研究了线性的机器人运动模型.上述其他文献(例如文献[20])在处理非线性的机器人运动模型时,一般通过近似线性化转为线性模型来研究,因而存在控制精度不高的问题.

为此,本文针对非线性、非完整约束的轮式移动机器人进行避碰避障的研究,选取线加速度、角速度作为其控制量来解决机器人的速度突变的问题,并通过精确反馈线性化的方法将非线性的模型转化为线性模型进行研究.本文针对线性模型引入了加速度变化障碍(acceleration change obstacle,ACO)的新概念,并在此基础上设计了可保证多机器人避障和相互避碰的算法.此算法中,把可能会导致碰撞的所有相对虚拟加速度变化定义成ACO;然后让每个机器人在ACO之外构建满足自己最大加速度约束的避碰虚拟加速度变化集合;在此集合中通过优化指标函数得到最优的虚拟加速度变化量,最后将其转换成轮式移动机器人实际的控制输入量.这种算法和基于速度障碍的相互避碰算法[10–16]相比,可以使机器人在避碰过程中的运动轨迹更为平滑.与基于速度跟踪控制的算法[17–20]相比,机器人的线速度和方向角的变化幅值更小,且角速度和线加速度的变化也更为平顺.另外,仿真比较显示本文所提出的算法的平均计算时间比文献[20]中的算法要短,因而在时效上也具有优势.

2 问题描述

2.1 符号

本文使用花体大写字母A表示向量集合,斜体大写字母A表示矩阵,黑体字母a表示矩阵向量,斜体小写字母a表示标量.定义如下的符号和运算:为矩阵向量x的欧几里德范数;x·y表示内积运算;定义运算aX={ax|x∈X},X ⊕Y={x+y|x∈X,y∈Y},其中⊕表示闵可夫斯基和;X Y=;D(c,r)=r}为圆心在c半径为r的圆盘.

2.2 机器人模型

本文研究的具有非完整约束的轮式移动机器人如图1所示,其中:x,y为机器人在全局坐标系XOY下的位置坐标,v为其行驶的线速度,θ为行驶的方向角.

图1 轮式移动机器人示意图Fig.1 Illustration of a wheeled mobile robot

在满足非完整约束的假设下,轮式移动机器人的运动学模型表示如下[4,20]:

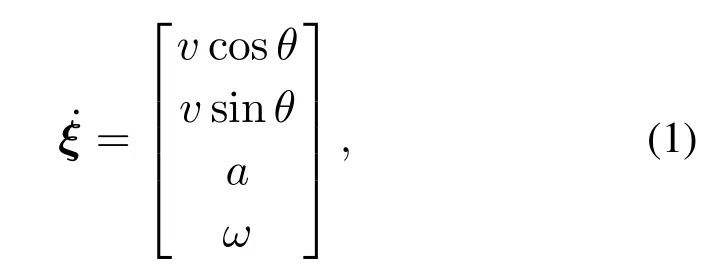
其中:ξ=[x y v θ]为当前时刻轮式移动机器人状态向量;a是机器人的线加速度;ω是角速度.定义u=[a ω]T为机器人的控制输入.

假设机器人的运动场景中同时存在多个障碍物和移动机器人,且其运动学模型都用式(1)来描述,本文的目标就是为每个机器人设计控制量u,使机器人在运动过程中避免与障碍物以及其他机器人发生碰撞.

本文采用的主要思路是首先将式(1)中的非线性模型通过反馈线性化转化为易于处理的线性模型,然后基于预测窗的方法为每个机器人构建可以保证其无碰行驶的虚拟控制量集合,最后在该集合中优化求解最优的无碰虚拟控制量并转换为机器人的实际控制量u.

3 加速度变化障碍的构建

本节首先通过反馈线性化把轮式移动机器人的非线性运动学模型转化成线性模型;然后根据线性模型构建加速度变化障碍,从而为后续的避障和相互避碰算法打下基础.

3.1 反馈线性化

考虑到轮式机器人的运动学模型(1)是受非完整约束的非线性系统,依据此模型设计基于预测的避障、避碰算法将会使得计算非常复杂,甚至影响计算效率.因此,本文首先对系统(1)进行反馈线性化处理.为此,先把系统(1)写成如下标准的非线性系统的形式:

因为式(2)中是一个2输入2输出的系统,且其相对阶等于系统的阶数,所以可以对式(2)进行反馈线性化.对于该系统,本文构造状态反馈控制律如下:

其中:d是一个虚拟控制量,α(ξ),β(ξ)是待确定的函数.根据反馈线性化的相关理论[22]可得

其中:r表示相对阶;表示f(ξ)对g(ξ)的r阶李导数;表示混合李导数.为了便于设计,

综合上式可得

利用式(8),系统(2)就被转换成如下的线性系统:

其中:p=h(ξ)=[x y]T和v=[vxvy]T为该线性系统的状态向量;a=[axay]T=d为系统(9)的虚拟控制量;η为系统的输出;I是单位矩阵.

3.2 加速度变化障碍

为了计算出机器人最优的无碰控制量,假设在未来一个较短的预测窗τ内线性系统(9)的控制量a是恒定的,即机器人做匀变速运动.然后基于匀变速运动学规律引入加速度变化障碍(acceleration change obstacle,ACO)的概念,其构造方法如下:

在二维欧氏空间中(见图2),定义移动机器人A和机器人(或障碍物)B的半径分别为rA,rB,令rAB=rA+rB.假设A,B在未来一段较短的预测窗τ内的加速度是恒定的,即做匀变速运动,则其运动轨迹描述如下:∀t∈(0,τ],

其中:pA=pA(0),pB=pB(0),vA=vA(0),vB=vB(0),aA=aA(0)和aB=aB(0)分别为A和B在当前计算时刻相对于原点的位置、速度和加速度,∆aA,∆aB为待确定的加速度变化量(见图2).则A,B的相对位置变化为

其中:vAB=vA−vB,aAB=aA−aB,∆aAB=∆aA−∆aB.若A,B在t时刻发生碰撞,则有AB(t)rAB,其示意图见图2.

Fig.2 两个移动机器人的相对运动示意图Fig.2 Illustration of the motions of two mobile robots

那么,可能导致A,B在预测窗τ内发生碰撞的相对加速度变化集合为

图3 加速度变化障碍示意图Fig.3 Acceleration change obstacle

其中q±(p,r)为经过原点的两条直线,其与圆心在p点半径为r的圆的两边分别相切,根据几何关系有

图4 速度障碍示意图Fig.4 Velocity obstacle

4 基于加速度变化障碍的避障、避碰算法

本节将在上一节得到的线性化的运动模型和加速度变化障碍的基础上,构建机器人的避障和相互避碰算法.

4.1 协作式避碰加速度变化集合

首先考虑简单的两个轮式移动机器人A和B的情况,每个机器人都采用上一节中构造加速度变化障碍的方法分别独立计算相对于彼此的加速度变化障碍由定义式(14)可知设机器人A和B的线加速度的最大值分别为则其相对线加速度的最大值为可选取的加速度变化∆aAB需满足约束即∆aAB∈D(−aAB,).则集合D()是满足最大相对加速度约束的无碰相对加速度变化的集合,将其表示为那么移动机器人A和B在预测窗τ内不发生碰撞的一个必要条件是

根据协作式避碰原则,机器人A,B主动独立计算并执行自己的加速度变化量∆aA,∆aB以使∆aAB=∆aA−∆aB满足式(17).为了体现公平性,相对加速度变化量∆aAB应该平均分配给两个机器人,即令

另外,每个机器人的加速度变化要满足各自最大加速度约束条件即

基于上述要求,机器人A,B用于避碰的加速度变化量的取值集合可以分别设可以证明这两个集合的闵可夫斯基差集是集合的子集:

因此,要为每个机器人提供无碰撞的加速度变化可行集合,需要首先计算其相对加速度变化量的可行集合考虑到可能是非凸的,为了提高算法的计算效率,用一个凸半平面C来代替,其满足如下两个条件:

同样可以证明其闵可夫斯基差集是C的子集.

下面来求解半平面C.考虑到满足式(18)约束的半平面C有无数多个,选取其中能最大化集合C ∩的那个,可通过下述方法求得.定义为集合的凸包(convex hull,CH),用符号∂表示这一闭集的边界.此边界上最接近原点的点表示为w,其数学定义如下:

其中n为w点处的法线向量,示意图见图5.

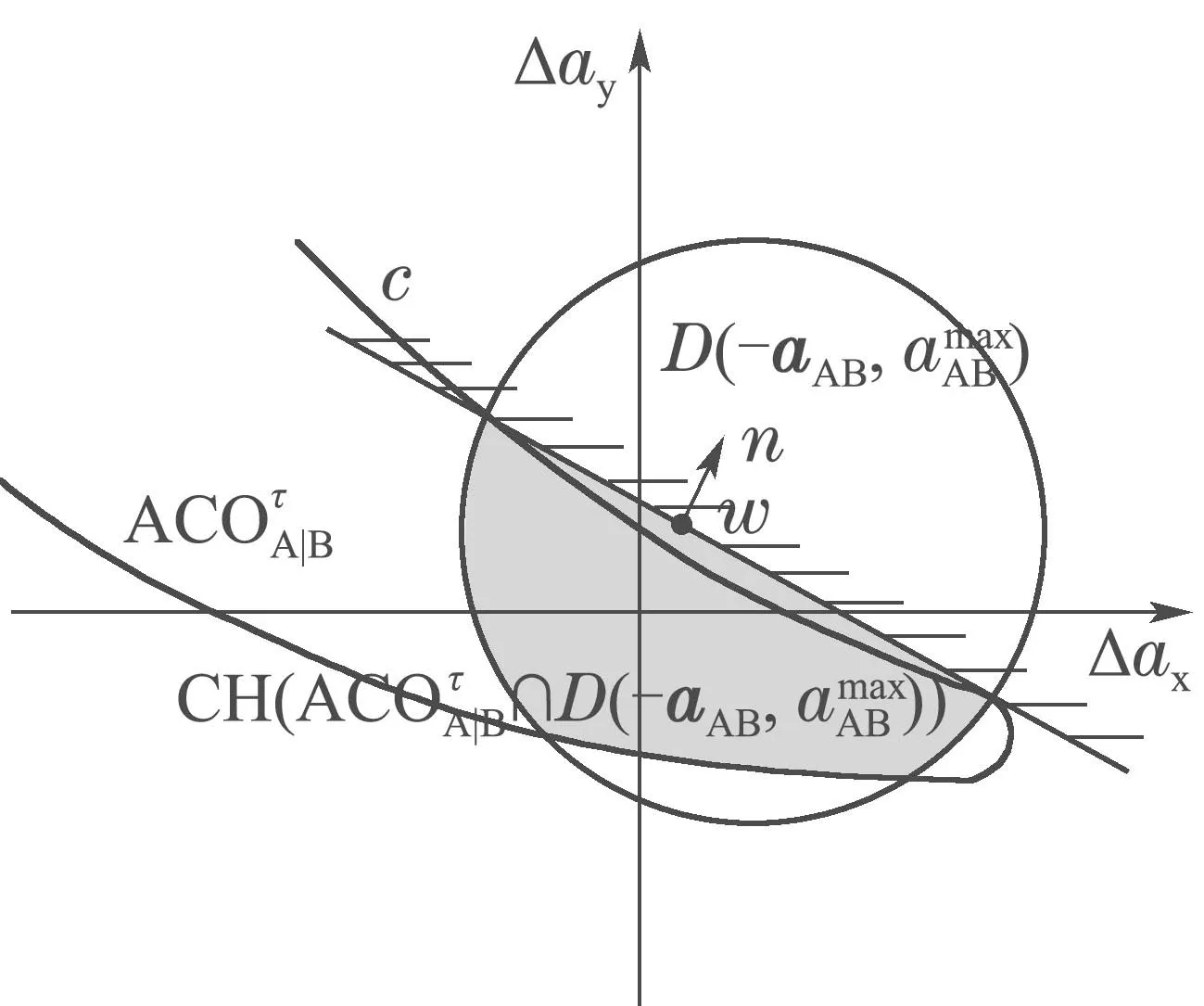
图5 半平面C(斜线标注的区域)的示意图Fig.5 The half-plane C (region marked with slashes)

图6 和(斜线标注的区域)的示意图Fig.6 and(regions marked with slashes)

其示意图见图6.

类似可得移动机器人B用于躲避A且满足最大加速度约束的避碰加速度变化集合为

4.2 多移动机器人的最优相互避碰和避障方法

其是由多个半平面围成的凸集,见图7.

图7 移动机器人A的(灰色区域)示意图Fig.7 Illustration of (grey region)for robot A

其中性能指标J的定义为

综合式(8)(29)可得机器人A在避碰预测窗τ内的最优实际无碰控制量如下:

由于以上算法构造过程中的机器人A具备一般性,其他任一移动机器人均可采用与之相同的方法独立求解各自的最优实际无碰控制量.因此本文的算法是分布式的.另外需要注意的是,如果计算出式(28)中的避碰加速度变化集合为空集,即当前时刻预测未来的τ时间段内不存在可以避碰的控制量,则令机器人以最大的减速度进行减速,以尽量减轻可能发生的碰撞所造成的危害.在减速的过程中,机器人仍然在每个采样时刻利用探测到的信息来重新计算集合一旦其变为非空集合则立即求解和执行避碰控制量.

5 仿真验证

本节通过MATLAB仿真来展示本文所设计算法的有效性,并与文献[20]中的基于控制障碍的CO算法进行对比.仿真中选取采样周期为0.1 s,避碰预测窗τ=2 s;所有移动机器人的半径都设为r=0.35 m,最大线加速度都为1 m/s2,每个机器人的期望速度的大小为定常值1 m/s,方向由各自的当前位置指向目标位置.

仿真1 两个移动机器人A,B初始位置分别位于[0 m,0 m]以及[10 m,10 m]处,初始线速度都为1 m/s,初始行驶角分别为初始线加速度和角速度都为0.仿真中两个机器人需要互换位置,因而在相会处会避免发生碰撞.

采用本文的ACO算法和文献[20]中的CO算法的移动机器人运动轨迹见图8.可见,两种避碰算法皆可实现轮式移动机器人的无碰撞运动,且机器人的运动轨迹相似.

图8 分别采用两种不同算法时机器人的运动轨迹Fig.8 Motion trajectories of the robots when using two different algorithms,respectively

但由图9可见,采用本文避碰算法时,机器人A在避碰过程中线速度和角度的变化幅度都小于采用文献[20]中的CO算法得到的值.图10展示了机器人A采用这两种算法时的控制量变化,可以看出机器人A的避碰控制量在CO算法下的波动比在本文ACO算法下更为剧烈,这会对机器人的驱动装置提出更高的性能要求,也更容易使其发生磨损.因此,本文所设计的算法更为合理和实用.

图9 分别采用CO和ACO两种算法时机器人A的状态对比图Fig.9 Comparison of the states of robot A under algorithm CO and ACO,respectively

图10 分别采用CO和ACO两种算法时机器人A的控制量对比图Fig.10 Comparison of robot A’s control inputs under algorithm CO and ACO,respectively

仿真2为了分析本文所提出的ACO算法的计算效率,取不同数量的移动机器人分别进行避碰仿真,记录在不同数量下平均每个机器人每次计算出各自的最优控制量的平均时间,并且与文献[20]中的CO避碰算法进行对比,统计结果见图11.可见,两种算法的平均单次计算时间都与机器人的数量成近似线性关系,因而具有良好的可扩展性.相比之下,本文算法比文献[20]中的算法需要的平均计算时间要更短,因而在计算效率上优于文献[20]中的算法.

图11 两种算法的平均计算时间对比图Fig.11 Comparison of average computation time needed by the two algorithms

仿 真3考虑3个移动机器人A,B,C和一个以线加速度0.1 m/s2做匀加速运动的移动障碍物O,初始二维坐标位置分别为[0 m,0 m],[10 m,10 m],[0 m,10 m],[10 m,0 m],即位于二维平面的4个角上.其初始线速度都为1 m/s,初始行驶角分别为即位于对角位置的机器人或障碍物向对方的方向运动.移动机器人A,B,C的初始线加速度和角速度都为0.图12展示了本文算法在轮式移动机器人相互避碰及同时躲避障碍问题上的有效性.

图12 机器人A,B,C躲避移动障碍物O的运动轨迹Fig.12 The motion trajectories of three robots A,B and C avoiding the moving obstacle O

6 结论

针对轮式移动机器人的相互避碰和避障问题,本文首先对其运动学模型进行了反馈线性化,然后在得到的线性模型的基础上提出了一种适用于非完整约束系统的相互避碰算法,弥补了已有的基于速度障碍和速度跟踪方法的不足,为移动机器人提供了平滑的运动轨迹,而且计算效率也具有优势.考虑到本文的避碰算法只用于同类型机器人之间的相互避碰,下一步的研究可将本算法推广到不同类型的移动机器人之间的相互避碰中.另外,考虑到实际应用中,机器人的角加速度也会存在约束,因此针对机器人在避碰和避障时的角加速度性能进行研究也是有待解决的问题.