欠驱动刚体航天器奇异避免的反步姿态控制

夏德银,常海波

(北京控制与电子技术研究所,北京 100038)

1 引言

欠驱动机械系统是一类控制输入个数小于系统自由度的控制系统,它广泛地存在于机器人、航空航天等各个领域,由于控制输入个数的减小,较大地增加了系统的控制难度,因此它成为控制系统的研究热点之一.针对欠驱动机械系统,研究人员已经提出了较多的控制方法,例如Spong等人[1–2]提出了基于能量的控制方法;Su等人[3]给出了PD部分反馈线性化的控制方法;Xia等人[4–6]分别设计了基于奇异避免的能量控制器、基于神经网络补偿摩擦的奇异避免能量控制器以及基于模糊神经网络补偿摩擦的奇异避免能量控制器等.

欠驱动航天器是一类具有强非线性和强耦合性的复杂机械系统.针对欠驱动航天器的执行机构出现故障或者缺失的状况,已经出现了较多有价值的研究成果.金磊等人[7]提出了线性二次型调节器(linear quadratic regulator,LQR),用于实现三轴角速度的稳定控制,其控制性能与初始姿态有一定的关系;黄兴宏等人[8]设计了分段解耦的姿态控制器,每一步解耦的前提是前面分段的控制误差要尽量地趋近于零;宋道喆等人[9]给出了零角动量逆最优的稳定控制器,对输入不确定性具有一定的鲁棒性;桂海潮等人[10]表明仅在带有两个非共轴的飞轮时,航天器姿态才有可能满足局部可控,非光滑控制器才能使得航天器的姿态镇定;阳洪等人[11]提出了反步控制器,只是所应用的运动学模型未考虑失控轴的角速度,给出的反步控制器存在奇异性,需要证明在奇异点姿态控制系统也是稳定收敛的;郑彦琴等人[12]给出了一种复杂的连续时变控制律,通过引入辅助变量和设计中间虚拟变量使得系统的参数趋于稳定.

综上所述,研究结果表明欠驱动轴角速度快速收敛是航天器姿态系统稳定收敛的重要前提;具有奇异性的姿态系统控制器,需要证明在奇异点姿态控制系统也是稳定收敛的.由此本文提出了一种奇异避免的反步非线性连续控制器:

1)基于欠驱动刚体航天器的动力学模型和利用(w,z)参数表述的运动学模型,考虑失控轴的角速度,设计了反步控制器,利用三通道之间的强非线性和强耦合性实现了驱动轴角速度和欠驱动轴角速度在较短的时间内快速地收敛到稳定状态;

2)通过构造合适的李雅普诺夫函数,推导得到了奇异避免的非线性连续控制器,成功地避免了反步控制器的奇异性.

最终,为了检验本文提出的奇异避免的反步控制器的性能,另外进行了数值仿真实验,实验结果表明本文提出的控制器具有较好的控制性能.

2 数学模型

2.1 动力学模型

本文使用的航天器姿态动力学方程[12]如下所示:

其中:ω=[ωxωyωz]T表示航天器姿态角速度;˜ω表示反对称方阵;T=[TxTyTz]T表示控制力矩;J=diag{Jx,Jy,Jz}表示航天器转动惯量.

为了不失一般性,假定刚体航天器绕Y轴的控制力矩Ty缺失,则航天器动力学方程转化为如下形式:

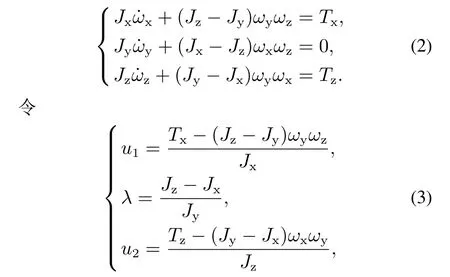
其中:u1,u2表示航天器姿态系统的控制输入,λ表示常数,一般情况下λ0.则式(3)可以表示为如下形式:

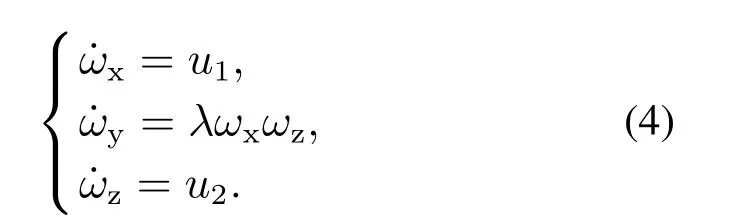
2.2 运动学模型

本文以(w,z)参数[12]描述的航天器姿态系统运动学方程如下所示:

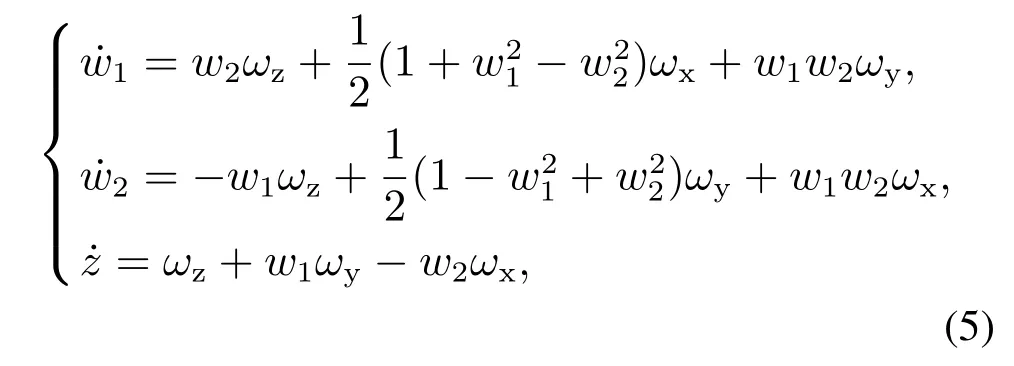
其中w1,w2,z表示航天器姿态.

3 控制器设计

本文首先设计理想的姿态角速度ωxd,ωzd,其次在理想的姿态角速度的基础上,推导得到奇异避免的反步控制器,完成航天器姿态控制系统的稳定控制.

3.1 ωxd,ωzd设计

为了便于设计理想的姿态角速度ωxd,ωzd,本文构造的李雅普诺夫函数如下所示:

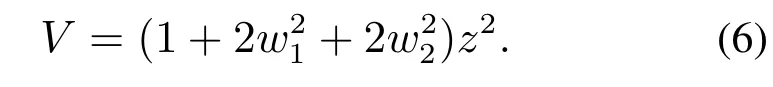
由于V0为半正定函数,对其求导可得

根据式(5)可得

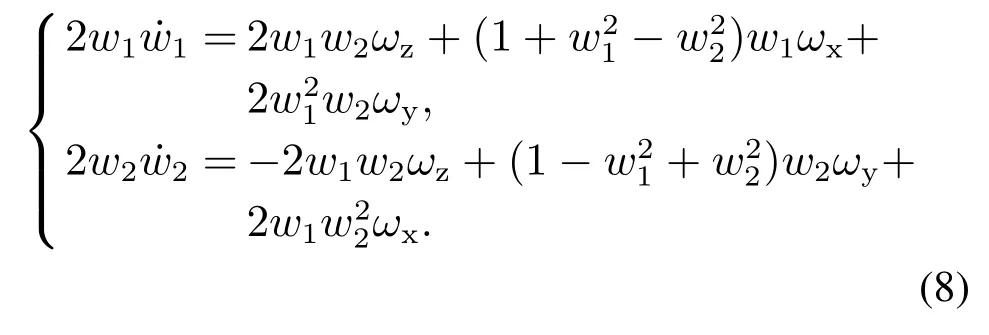
将式(8)代入式(7)可知

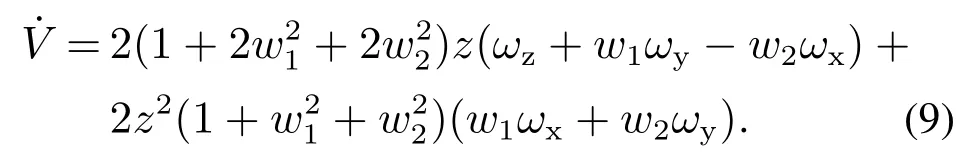
将式(9)中的wx,wz利用理想角速度wxd,wzd代替,其中本文设计的理想姿态角速度的表达式如下所示:

注1δ>0表示极小正数,此时式(10)中0,避免了wxd,wzd的奇异性.

注2k1>0,k2>0,k3>0,k4>0为正数.

由式(9)–(10)可得

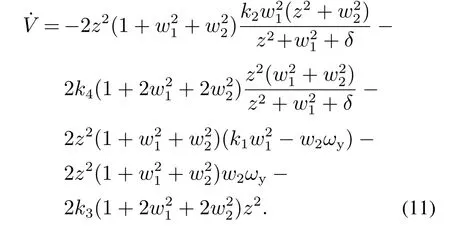
对式(11)进行简化可得

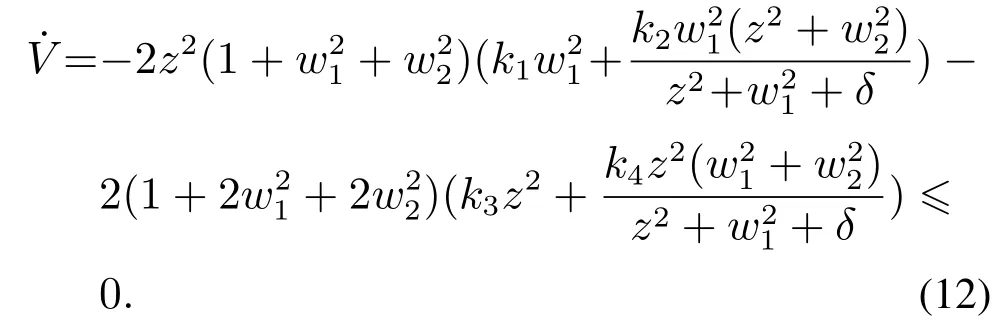
注3由式(12)中0可知,在式(10)中理想的姿态角速度ωxd,ωzd的作用下,航天器姿态参数w1,w2,z收敛到稳定状态.

3.2 奇异避免的反步控制器设计

根据式(10),为了推导得到奇异避免的反步控制器,完成航天器姿态控制系统的稳定控制,本文重构的李雅普诺夫函数如下所示:

由式(8)可知

进一步推导得到

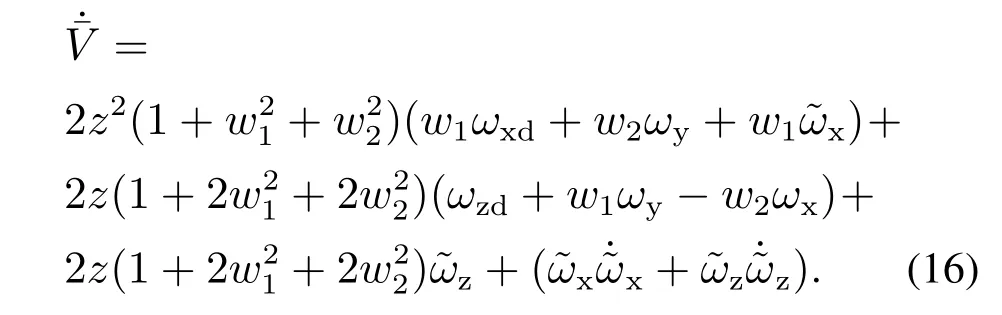
将式(10)代入式(16)可得

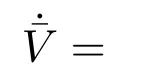
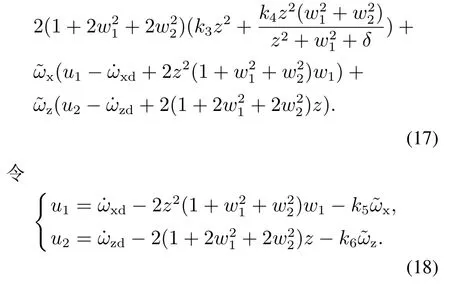
注4k5>0,k6>0为正数.可得

注5由式(19)可知0,可知在本文给出的奇异避免的反步控制器的作用下,欠驱动刚体航天器的姿态控制系统稳定.

4 仿真研究

为了检验本文提出的奇异避免的反步控制器(singularity avoidance back-stepping control,SABSC)的性能,将SABSC与欠驱动航天控制器的运动学和动力学模型组成闭环系统进行数值仿真分析.其中航天器硬件结构参数在表1中给出.SABSC的主要控制参数在表2中列出.

表1 航天器硬件结构参数值Table 1 Hardware structure parameter values of spacecraft

表2 SABSC参数值Table 2 Parameters of SABSC

在SABSC的作用下,假定航天器的初始姿态角速度均为零,初始参数分别为

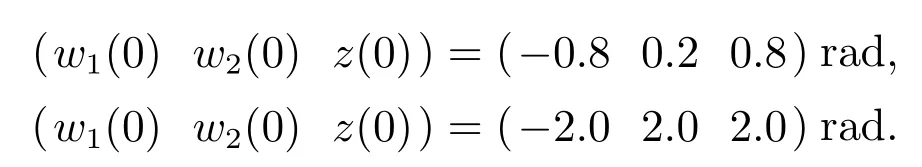
航天器姿态系统输出的角速度曲线等在图1–2中给出.

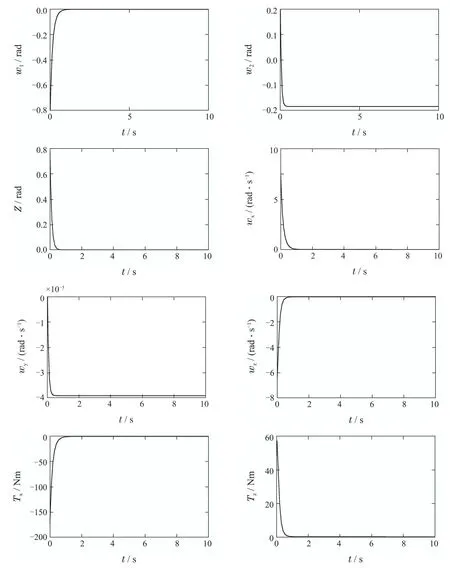
图1 w1(0)=−0.8 rad时航天器姿态系统参数的变化曲线Fig.1 Parameters change curves of spacecraft attitude system when w1(0)=−0.8 rad

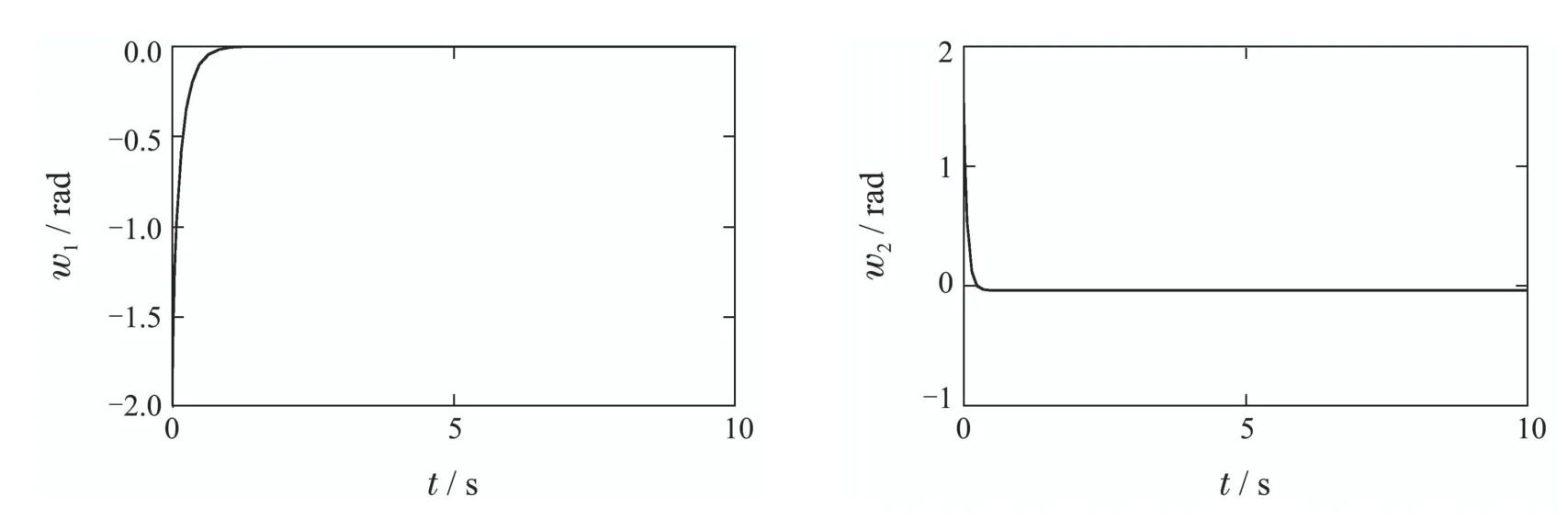
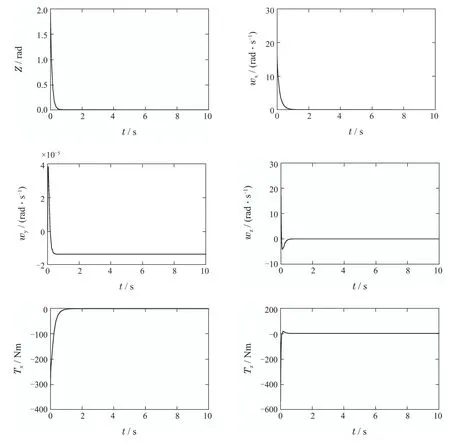
图2 w1(0)=−2.0 rad时航天器姿态系统参数的变化曲线Fig.2 Parameters change curves of spacecraft attitude system when w1(0)=−2.0 rad

由图1可知,在本文提出的奇异避免的反步控制器(SABSC)的作用下,欠驱动刚体航天器的参数w1,w2,z,wx,wy,wz都在1 s的时间内收敛到稳定状态.其中驱动轴的姿态参数w1,z,wx,wz收敛到零,欠驱动轴的姿态参数w2,wy在三通道之间耦合控制力的作用下分别收敛到某个常值状态,并且随着刚体航天器飞行状态的不断变化,继续保持在这一状态稳定飞行,表明本文设计的SABSC具有较好的控制性能.

由图2中航天器姿态系统参数的变化曲线可知,当初始参数为(w1(0)w2(0)z(0))=(−2.0 2.0 2.0)rad时,在本文提出的SABSC的作用下,w1,w2,z,wx,wy,wz等参数也都在较短的时间内收敛到稳定状态,表明SABSC具有较好的控制品质,使得驱动轴和欠驱动轴的姿态参数具有较好的动态特性,快速地趋近并且保持在稳定状态.

5 结论

本文主要研究了欠驱动刚体航天器姿态系统的稳定控制问题,根据航天器姿态系统的动力学方程和利用(w,z)参数表述的运动学方程,本文提出了SABSC,当绕Y轴的控制力矩Ty失效时,用于完成航天器姿态系统的稳定控制.由数值仿真的实验结果可知,w1,w2,z,wx,wy,wz都在较短的时间内收敛到稳定状态,表明本文给出的SABSC 具有较好的快速性和收敛性.