灌溉管网调压池布置与管径同步优化研究

高 园，莫腾飞，何武全，娄宗科

（西北农林科技大学，陕西 杨凌 712100）

0 引 言

灌溉管道系统以其节水、省地、适应性强、灌溉效率高等优越性被广泛应用。按照获得压力来源，可将其分为机压式与自压式2 类[1]。前者依靠水泵，后者依靠自然地形落差。当水源水面低于灌区高程或不足以提供灌溉管网所需压力时，可布置水泵等增压设备加压；当地形条件可利用时可采用自压式管网系统，可减少系统的运行费用。但随着管道灌溉技术的应用与推广，落差大、管线长的大规模灌区越来越多，输水过程中会引起管道水力条件的急剧变化，严重时甚至引起爆管[2]，针对这种情况则需要减压以控制管道压力。一般有机械减压和水工减压2 类方案用来消减多余水头，机械减压方案有调压阀，减压阀等；水工减压方案有调压室，调压池等。

现阶段对长距离加压灌溉管网已有了一定研究[3-6]，但对需减压的灌溉管网研究很少。传统灌溉管网布局优化是寻求水源到各配水节点间的连接路线最短的管网结构形式，从宏观上控制投资，只考虑管网投资[7-10]。现行的行业标准及工程经验主要针对控制面积在8×105m2以下的灌区，对于规模更大，管网系统更加复杂的灌区仍缺少理论研究、行业标准及工程经验[11]。因此对于大规模自压灌溉管网，如何确定减压级数与减压设施位置则需要通过经济分析。研究人员对传统管网优化使用的线性规划法[12]、非线性规划法[13]、人工神经网络法[14]、遗传算法[15]等方法可提供一定参考。

为此，以自压式树状灌溉管网为研究对象，将调压池与干管管网作为一个整体[16]。建立目标函数时同时考虑调压池造价和管道造价，对调压池布置位置和管径组合采用基于整数编码的双重编码方法，以获得灌溉管网调压池布置与管径组合同步优化方案。

1 自压式树状灌溉管网调压池优化思路

大规模自压式灌溉管网的管道压力沿管线自上而下逐步加大，分干管首部的压力也随之增加。布置调压池的目的是同时保证管道安全运行和造价经济合理。调压池兼顾调压和调流功能，在调压方面，在管网适当位置布置调压池，从调压池布置高程处重新累积水头，以满足下游节点压力需求；在调流方面，调压池有效容积为下游配水节点灌溉周期内的灌溉用水量需求，当进水管流量小于出水管流量，可为下游管道补充流量；当进水管流量大于出水管，为防止上游流量过大导致池水溢出造成浪费，布设溢流设施，将可能的溢流水量引入附近林带中。

大规模灌溉管网布置调压池可减小干管直径，减少管网投资。调压布置位置和级数与地形落差、管道长度、管道承压力等因素有关，管道承压能力越低，地形落差越大，则需要设置的调压级数就越多。故调压池的建造费用也不可忽略，且与管网造价为此消彼长的关系，因此调压池布置与干管管径同步优化一方面要降低管网投资与调压池造价，另一方面要保证配水节点的压力与水量需求。通过对比分析，寻求调压池布置与干管管径组合同步优化的最优方案。为方便编码计算，由同一座调压池（或水源）供水的相邻2节点之间连接管段仅由同一种标准管径组成，这样既可减少管道连接件的费用，又方便管道施工与安装。

2 优化设计模型

2.1 目标函数

本文研究的自压式树状灌溉管网系统由干管、分干管、支管组成，原理如图1 所示。干管减压方式为调压池，即水工减压，从调压池布置高程处重新累积水头，一方面满足下游配水节点的水头于水量需求，另一方面保证管道压力不超过其承压力；干管分别向调压池和分干管输水，分干管则向支管供水，支管采用减压阀减压，即机械减压，减压阀安装在支管首部，以削减多余水头，保证管道运行安全。

输水管与配水管为2 种不同材质管道，输水管连接水源与调压池以及相邻2 座调压池，仅负责向各调压池输送水流；配水管由水源或调压池接出，满足下游配水节点灌溉水量需求与工作压力需求。

图1 调压池布置示意图 Fig.1 Layout of pressure regulating tank

管网系统总落差与管道的承压等级是决定管道是否需要减压及减压强度的主要因素，管道承压等级越低，减压级数就需要设置的越多。在管网布置形式，各配水节点高程、流量、最低水头要求、管道承压力已知的情况下，调压池的布置优化与管径同步优化就是寻求一组能满足配水节点水量、压力、管径与流速要求的情况下，调压池造价与管道造价之和最小的组合，其数学模型为：

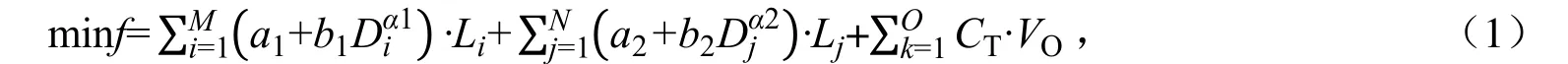
式中：f 为灌溉管网总造价（元），由输水管道、配水管道及调压池3 部分造价构成。M、N 分别为输水管道和配水管道的管段数量；Di、Dj、Li、Lj分别为输水管道和配水管道的直径（mm）与长度（m）；a1、b1、α1、a2、b2、α2分别为输水管道与配水管道造价参数；O 为调压池数量；CT为单位容积调压池造价（元/m3）；VO为调压池容积（m3）。

2.2 约束条件

1）流量约束：任一管段流量为该区域下游所有配水节点流量之和；

2）压力约束：包含工作压力与静水压力约束

①工作压力

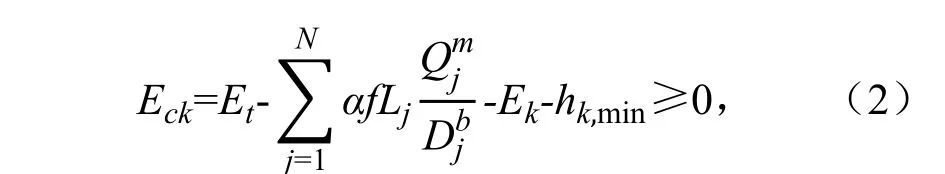
式中：t=0，1，2，…，n; j=1，2，…，N。

②静水压力

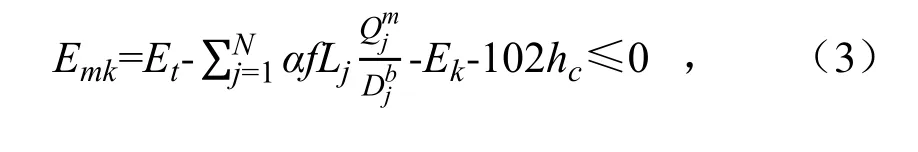
3）流速约束

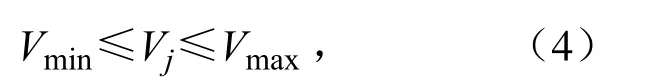
式（2）、式（3）、式（4）中：Eck为管道工作压力约束（m）；Emk为管道承压力约束；Et为调压池布置高程（m），E0（即t=0）为水源供水；采用《喷灌工程技术规范》[17]公式计算管道水头损失，Qj为第j 段管段流量（m3/h）；Lj为第j 段管段长度（m）；α 为考虑局部水头损失的系数；f、m、n 为与管道材料有关的系数；Ek为第k 个配水节点高程（m），；hk,min为第k个配水节点最小工作压力；hc为管道承压力；Vmin、Vmax为分别为管道最小流速和最大流速，二者分别为了防止管道淤积与产生水击破坏。

3 整数编码的遗传算法

3.1 编码设计

灌溉管网优化需要对调压池的布置形式与管径组合进行同步优化设计，本文以各配水节点为基础，采用双重编码[18]。调压池布置位置的确定，实质上是对管网进行分区，每个调压池对若干配水节点进行灌溉，与水源共同完成整个灌区的灌溉。为方便优化分析，调压池布置位置为各个配水节点高程处，故可用整数编码，对于有n 个配水节点的管网，随机生成0～n 共n+1 个整数，生成的整数即为供水点，其中0 表示由水源直接供水灌溉。如随机生成的[0 0 0 1 1 3 3]表示共设2 座调压池，其中水源（0 节点）控制1、2、3 节点；第1 个调压池布置在节点1 位置，满足节点4、5 的灌溉需求；第2 座调压池布置在节点3 位置，满足节点6、7 的灌溉需求；每个配水节点从理论上可由布置在上游任何一个节点的调压池提供水量，考虑到配水节点工作压力的需求，在编码时，主动排除地面高差小于工作水头的节点，这样可以减小不可行解的产生，提高求解效率。管径值同样采用单调递增整数编码表示，如有5 种可供选择的管径规格，分别为0.15、0.25、0.3、0.4、0.5 m，则可用0～4 之间的任一整数表示一一对应，如随机产生的某种管径组合[3 2 0 3 1 3 2]从左到右依次表示水源、各个调压池连接干管管段的管径。

3.2 目标函数及适应度函数设计

前文所述的双重编码方法可以保证管网的连通性，对式（2）和式（3）的压力约束，以及式（4）的管道流速约束，本文采用罚函数法处理，故构造如下适应度函数：

式中：Vj为第j 段管道的实际流速（m/s）；λ 为惩罚因子。

3.3 遗传操作

遗传算法的3 个基本操作分别为选择、交叉、变异[19]。本文采用轮盘赌选择个体，采用单点交叉法进行交叉运算，交叉概率Pc 取0.7；采用变异概率进行变异计算，变异算子Pm=0.3。同时为了使函数不陷入局部最优并保持种群多样性，参与遗传的个体每次只按一定比例选择，待算法的交叉变异过程完成后，把该部分个体重新插入到种群中，与剩余种群重新组成新种群，进行遗传操作的个体继续从新种群中按一定比例选取，一直循环到程序终止[20]。

4 工程应用实例

为进一步验证本文所提方法实际应用效果，以某自压式树状灌溉管网为例，编制了自压式树状灌溉管

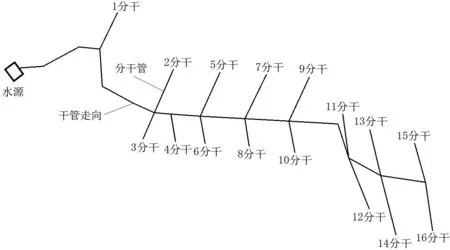
图2 管网地形简图 Fig.2 Topographic map of pipe network

灌区管网共10 个节点，其中0 节点为水源，各配水节点地面高程与供水流量如表1 所示，相邻2节点间的管线长度如表2 所示。本文灌溉管网工程网调压池布置与管径同步优化程序，并将优化结果与人工经验法确定布置方案进行对比。

4.1 基本数据

该灌溉管网地形图简图如图2 所示。灌区海拔高程820～680 m，地势南高北低，相对平坦、开阔。管网工程控制面积9×106m2，首端为沉砂池，具有沉积泥沙和调节用水的功能，是整个管网系统的水源工程，水源由工程南侧干渠分水口直接进入。灌溉管网总体采用“管道输水，自压滴灌”的灌溉方式，布置调压池后，系统采用干管轮灌，分干管与支管续灌的工作制度。考虑地形特点与设计经验，初步确定的调压池布置形式如图3 所示，图3 中红、绿、蓝线段依次表示水源、第1 座调压池、第2 座调压池负责的灌溉节点；玫红、青色虚线分别表示水源与第1 座调压池、2 座调压池之间的输水管。输水管道采用预应力钢筋混凝土管，配水管道采用承压力为0.63 MPa 的PVC-U 管道，2 种管材造价分别见表3、表4。

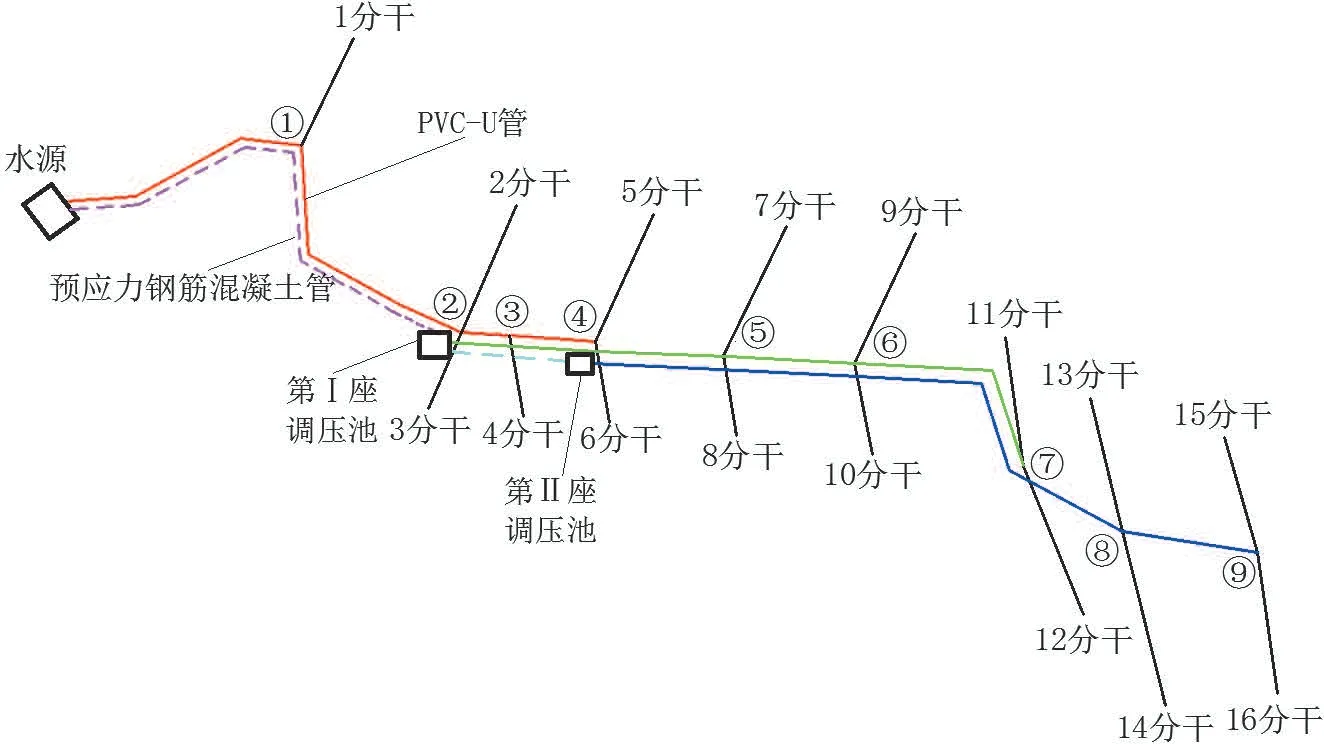
图3 调压池布置示意图 Fig.3 Layout of pressure regulating tank determined

表1 节点地面高程与供水流量 Table 1 Ground elevation and water supply flow of the node

表2 干管管段长度 Table 2 Main pipe length

表3 预应力钢筋混凝土管管道单价表 Table 3 Unit price list of prestressed reinforced concrete pipe

表4 PVC-U 管管道单价表 Table 4 Unit price list of PVC-U pipe

4.2 控制参数选取

在诸多遗传算法的控制参数中，群体规模、最大遗传代数对优化结果的精度影响较大，因此需对这2 个参数进行组合分析，以确定合理取值，其他参数参考一般情况下的取值即可[21]。

图4 遗传算法确定的调压池布置示意图 Fig.4 Layout of pressure regulating tank determined by genetic algorithm

4.3 优化结果分析

本文利用MATLAB 9.4 编程，在调压池布置优化与管径同步优化中，初始种群规模为100，遗传终止代数为200，代沟GGAP=0.7，得出符合实际且造价最小的方案。优化计算得到的管网布置图如图4 所示，图4 中颜色对应的线段与虚线同图3，管径组合优化结果见表5。

将遗传算法优化计算结果与人工经验法进行比较分析，二者均布置2 座调压池，将管网分为3个区域，且都由水源控制1～4 节点灌溉，2 种方法第1 座调压池均布置在节点2。其中前者确定的第1 座调压池负责5～6 节点灌溉需求，调压池有效容积409.6 m3。后者设计的第1 座调压池控制5～7节点，调压池有效容积614.4 m3。前者确定的第2座调压池布置在节点5，控制7～9 节点，容积716.8 m3；后者设计的第2 座调压池布置在节点4，控制8～9 节点，有效容积512 m3。遗传算法计算的PVC-U 配水干管总长度10 973.7 m，较人工经验法（12 473.0 m）减少12.02%，系统总投资464.80万元，较人工经验法（561.58 万元）减少17.23%。由图5 可以看出，本文布置方式各节点工作压力较人工经验法更均衡，配水节点最大压力均低于40 m，因此采用基于整数编码的双重编码遗传算法更为合理。

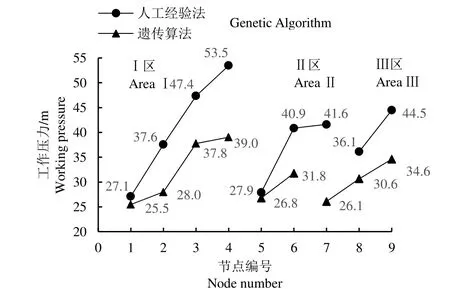
图5 干管配水节点工作压力 Fig.5 Working pressure of water distribution node of main pipe

5 讨 论

大高差长距离管网系统布置调压池可通过调节管道压力与流量来改善管道水力条件的急剧变化，同时也可减少管网投资。相关学者虽然做过大量研究，但都单一考虑管道系统。在管网系统布置调压池加大了管道布置模式及管径选择的复杂程度，提高了管网经济性分析的难度。因此，合理布置调压设施与管径选择是提高工程设计水平的重要措施。

前人优化研究往往将其他调节构筑物作为一个次要因素考虑，本文则强调了调压池在整个系统中的关键作用，明确了管网系统中调压池的布置位置及数量与管道之间的互相影响，在此基础上建立了调压池布置位置与管径组合的同步优化。针对同步优化问题的特点，设计了基于整数编码的双重编码方式，根据设计人员的经验确定出可能布置调压池的节点位置和可供选择的管径组合，将设计经验融入计算的初始阶段，有效地提高了优化算法的计算效率和可行性。同时借鉴前人优化所采用的压力约束与流速约束等，以及对约束条件的处理办法，最终得出的调压池布置位置与管径值无须进行调整，有效避免了圆整化处理对解的可行性与最优性的破坏，提高了算法的优化效率。

本文采用的优化方法与人工经验法均考虑将调压池布置在各分干管入口处，在水源均负责前4 个节点的灌溉需求的前提下，2 种方法得到的2 座调压池总容积是相等的，这是由于本文定义调压池容积为相同灌溉周期内的各节点水量总和，故两座调压池的总容积为剩余5 个节点灌溉周期内水量之和。人工设计确定的管道直径一般着重考虑满足节点水头需求，本文遗传算法则同时考虑节点水头与管道造价及调压池造价的影响，并在实际操作中采用不同交叉概率，变异概率等，反复运行优化程序，选取总造价与水力性能最优的方案作为最终方案。因此得到的管径大小、管道总长度都较人工经验法更科学合理。根据压力约束公式，管道直径与长度对管道压力影响更显著，因此优化得到得更为合理的管径与长度使得同一区域内各节点水头更为均衡。

本文优化研究对丰富管网系统调节构筑物布置优化设计理论有重要的意义，同时也可对其他领域调节设施的布置有一定的借鉴作用。

6 结 论

1）将干管管网与调压池作为一个整体，提出并建立了在自压式树状灌溉管网调压池布置与管径同步优化的方法与数学模型，并基于遗传算法，以二者造价之和最低为目标函数建立了优化模型，通过求解可得到调压池的布置方案与管径组合方案。

2）采用了基于整数编码的双重编码方法，优化得出的管径无须调整。采用罚函数法处理约束条件，优化结果表明，算法具有较高的精度。

3）对于大型自压式灌溉管网，干管布置调压池可有效降低管道工作压力，并降低工程总投资。结合实例，在调压池与管网系统造价之和最小模型下，与人工经验法相比，总投资减少17.23%，且各节点的工作压力更均衡。