双旋涡轮叶片不同参数下外流场模拟分析及优化
刘昭良,王金龙,苑成东,张夏琦,陈 辉
(1.山东科技大学,山东 青岛 266590;2.潍坊学院,山东 潍坊 261061)
0 引 言
上述常见搅拌器的研究中,涉及环境检测用的搅拌器且对于叶片参数对搅拌流场特性影响的分析较少,叶轮参数对于整个搅拌过程的影响至关重要,参数的选择在提高搅拌效率,增大产能,环保节能等方面具有不可替代的作用。影响搅拌器涡轮叶片的参数主要有:叶片数目、叶片片型、叶片有无开孔、叶片间距、叶片曲率、中心轴尺寸等,本文以叶片数目、叶片有无开孔、中心轴有无开孔为目标参数进行分析研究。基于此,采用CFD 流体软件,对首尾两端对称旋钮的双旋结构叶片进行研究,结合计算流体力学对于叶片片数、叶片有无开孔、中心轴有无开孔3 个重要参数,对搅拌区域的外流场影响进行系统的对比分析、优化,得出3 个因素的影响大小。
1 双旋叶片的分析模型
1.1 数值分析
对叶片外流场的分析,基于CFD 的三大守恒定律—质量、动量、能量守恒,雷诺平均的质量守恒和动量守恒方程表达形式为[17]:
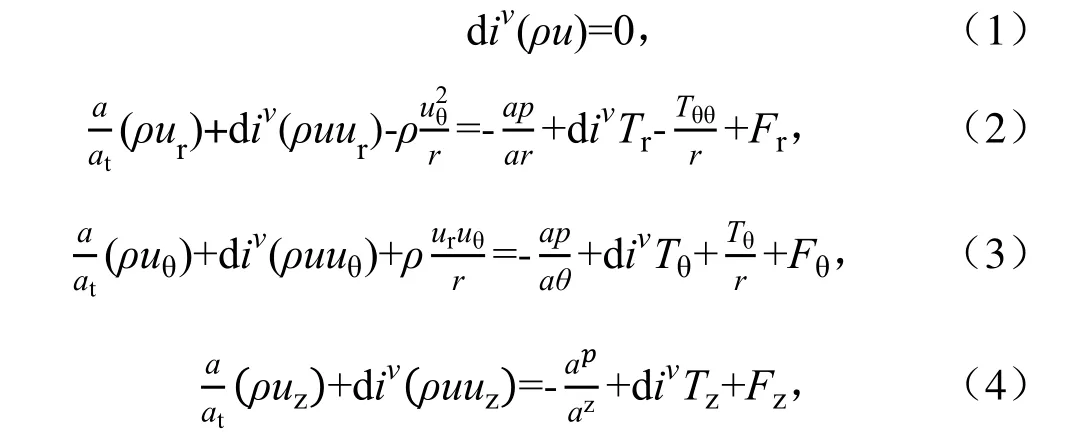
式中:u 为速度矢量;ρ 为密度;t 为时间;ur、uθ、uz分别为径向、切向和轴向速度分量;p 为修正压力;Fr、Fθ、Fz分别为作用于流体上的径向、切向、和轴向方向上的体力分量;Tr、Tθ、Tz分别为构成有效应力张量Ti的行向量。
1.2 模型的建立
分析所用涡轮叶片是基于贝塞尔曲线理论设计的涡轮叶片,贝塞尔曲线理论于20 世纪90 年代形成,其曲线在涡轮叶片设计及造型方面相比之前更加便捷,被广泛应用于航空、汽车等方面[18]。贝塞尔曲线根据特征多边形的控制点来定义,通过在起始点和终点之间构造多项式函数,即给定空间K+1 控制点Pi(i=0,1,2,…,k),这些控制点就组成贝塞尔曲线特征多边形[19],此时的曲线可以表示为:
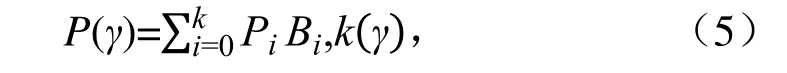
式中:参数γ 的取值为[0,1];Bi,k(γ)为k 次古典伯恩斯坦(Berstein)基函数,即插补函数。
通常在实际工程应用中,一般只用二次和三次贝塞尔曲线。涡轮双旋叶片,模拟过程中采用贝塞尔曲线模型,分析模型尺寸为:轴向涡轮高度40 mm,叶片厚度为1 mm,叶片采用三维旋钮曲面形式,外围外流场模拟尺寸为100、100、100 mm。
2 叶片外流场的模拟分析
搅拌器涡轮叶片影响因素对外流场影响的强弱,一般循环环流的个数以及环流的强弱来判断,环流个数越多、环流越强,对外流场的影响越强,搅拌效率越高。这是由于循环环流的存在,加速了相互之间的流动,减少了流动死区的出现。模拟分析设计了3 组模拟试验参数,在相同环境下对变量参数进行对比分析,通过观察其所形成的流场的流速图及压力图,得到变量参数对外流场的影响情况。
2.1 叶片数量与开孔情况的影响对比
研究对象为双旋涡轮的叶片数量与有无开孔,一般情况,叶片开孔后,会使得叶片表面附近的流场流速加快。其中,模拟分析中,第1 组,叶片数量分别为3、5、6,第2 组,分别在上述每个叶片上开相同大小的孔。2 组模拟,通过观察叶片数量对涡轮外流场的影响大小,得出叶片数量与有无开孔对外流场影响的情况,及这2 个因素间的对比,为了直观形象地将结果进行对比,将模拟分析结果绘于图1—图6。
1.3 思想政治教育工作方式方法单一。思想政治教育要取得预期实效,方法必须灵活多变,要把握其中的艺术性和创造性。思想政治教育的方法是否科学合理,关乎其任务完成与否与教育目的的实现与否 然而,在当前时代,国有企业的思想政治教育工作方式仍然停留在几十年前的方式,仍然是学文件、做讨论、听报告等形式,出于对上级领导的文件指示,不得不而为之的敷衍塞责。如一些国有企业将宣传材料发给员工,没有耐心细致地讲解,要求员工自行阅读,无视其接受程度,并强制其写思想汇报,成为员工的思想负担;还有些国企长年就是在宣传栏中书写点标语、粘贴点宣传画,而且更新频率很慢。

图1 3 叶片原始外流场图 Fig.1 3 Original blade outflow field diagram

图2 3 叶片开孔外流场图 Fig.2 3 Flow field diagram of blade opening
由图1、图3、图5 可知,3 叶片原始流速矢量图中,叶片在旋转时,左右两侧径向出现微弱的循环流动,流体经过微弱的双循环流动后撞向外壁,且在中心转轴附近的流速较低,这是因为涡轮在转动时,中心转轴为实心材质,阻碍了流体的流通性;5 叶片原始流速矢量图中,在涡轮的径向分布的双循环开始变得加强,且中心流速有所提高,开始有模糊的轴向流动边界;6 叶片原始流速矢量图中,已经在涡轮两侧形成明显的径向环流,中心区域整体流速提高,径向双循环的出现,强化了搅拌过程的效率,中心区域的流速加快,减少了搅拌的用时,中心区域出现了微弱的轴向流动,且界限较清晰。综合上述这3 组模拟分析中,6 叶片原始涡轮效果最为理想。

图3 5 叶片原始外流场图Fig.3 5 Original blade outflow field diagram

图4 5 叶片开孔外流场图 Fig.4 5 Flow field diagram of blade opening

图5 6 叶片原始外流场图Fig.5 6 Original blade outflow field diagram
由图2、图4、图6 可知,3 叶片开孔流速矢量图中,在开孔涡轮的两侧同样出现了较微弱的循环流动,双循环情况没有明显变化,由于叶片开孔后,流体在叶片间流动更加流畅,致使中心区域的流速有轻微提高,但影响不大;5 叶片开孔流速矢量图中,当5 叶片开孔后,涡轮两侧的双循环相交未开孔时明显加强,但仍不如未开孔的6 叶片双循环,开孔后的5叶片相较于开孔时径向循环流动位置下移且高速区域明显增多;6 叶片开孔流速矢量图中,开孔后的6叶片中心区域流速相较于开孔明显降低,且未开孔时涡轮两侧的双循环开孔后变弱,双循环中心位置下移,中心区域流速相较于开孔时明显下降。综合图1—图6 模拟分析,得出开孔后虽然在一定程度上加速了叶片表面的流动,但由于叶片表面的流动破坏了循环环流,使得整体的流动趋于低效率化,所以6 叶片无孔,搅拌效率最高。
2.2 叶片数量与中心轴开孔情况的影响对比
研究对象为双旋涡轮的叶片数量与有无中心轴开孔,一般情况,中心轴开孔后,会使得中心轴附近轴向流场流速加快。其中,模拟分析中,第1 组,叶片数量分别为3、5、6,第2 组,分别在上述每组的中心轴上开标准为21/64 的孔。2 组模拟,通过观察叶片数量对涡轮外流场的影响大小,对比中心轴的开孔情况,继而观察中心轴开孔情况对涡轮外流场的影响大小,分别得出叶片数量与中心轴开孔情况对外流场影响的情况及这2 个因素间对比的影响强弱,为了直观形象地将结果进行对比,将模拟的开孔情况分析结果绘于图7—图9。

图7 3 叶片中心轴开孔外流场图 Fig.7 3 Flow field diagram of central axis opening of blade
由图1、图7 可知,3 叶片流速矢量图中,中心轴开孔的涡轮外流场径向环流与未开孔的相比区别不是很大,但由于中心开孔后,流体可以从中心轴内流动,因此轴向流速要比未开孔的方案有所提升,且整个外流场的高速流动区域要比开孔的方案多。由图3、图8 可知,5 叶片流速矢量图中,相较于未开孔的方案,中心轴开孔的涡轮外流场流动较为紊乱,未开孔的涡轮外流场有径向环流的雏形,而开孔后则打乱了这一流动特性,使得环流被破坏,随之搅拌效率降低。由图5、图9 可知,6 叶片流速矢量图中,中心轴开孔的涡轮外流场径向环流彻底消失,整个外流场呈现无序的乱流状态,相较于未开孔的明显的径向环流双循环,开孔后搅拌效率明显会低很多。综合上述图7—图9 模拟分析,虽然轴向开孔后,加速了轴向流动,但由于轴向的流动给循环环流带来了破坏,使得整体的流动趋于低效率化,因此6 叶片原始无开孔为最佳方案,即方案的搅拌效率最佳。
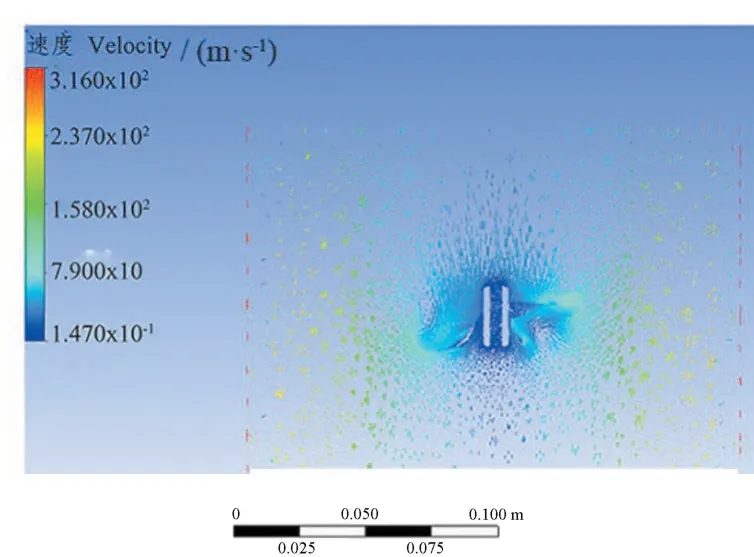
图8 5 叶片中心轴开孔外流场图 Fig.8 5 Flow field diagram of central axis opening of blade
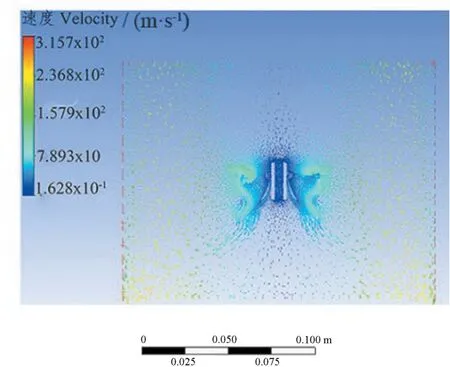
图9 6 叶片中心轴开孔外流场图 Fig.9 6 Flow field diagram of central axis opening of blade
3 叶片模型优化及分析
基于上述最佳方案6 叶片涡轮叶片模型,对其进行整体优化后,提出一种优化后的模型,对比优化前,为了直观形象地将结果进行对比,将模拟分析结果绘于图10、图11。由图10、图11 可知,优化前(图10),模型在以下方面存在缺陷,叶片外表面附近的流速较低;靠近外壁处流速较低。以上缺点是由于模型叶片与中心轴的接触是部分的接触,叶片固定强度较低,在搅拌过程中流体与叶片产生谐响应,降低了搅拌效率。叶片底部空间在搅拌过程中会产生乱流,破坏了循环的环流的产生,使得整体的环流效果较差,流速降低,搅拌效率下降。优化后(图11),模型进行了如下优化:将模型的叶片靠近中心轴的一侧完全与轴固定,相较于优化前,强化了叶片稳定性,减小了叶片在搅拌过程中的谐响应,降低了叶片因转动形成的压力对叶片的损伤,提高了叶片的稳定性,优化后的流速矢量图,环流更加明显,搅拌效率更高。综合上述图10、图11 的模拟分析,得出优化后的模型解决了叶片的接触问题和中心轴底部的分布空间问题,强化了环流,搅拌效果得到提高。
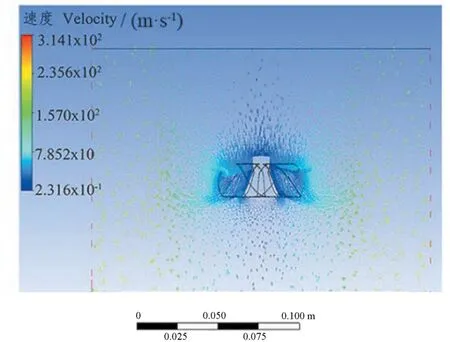
图10 优化前流速图 Fig.10 Flow rate diagram before optimization
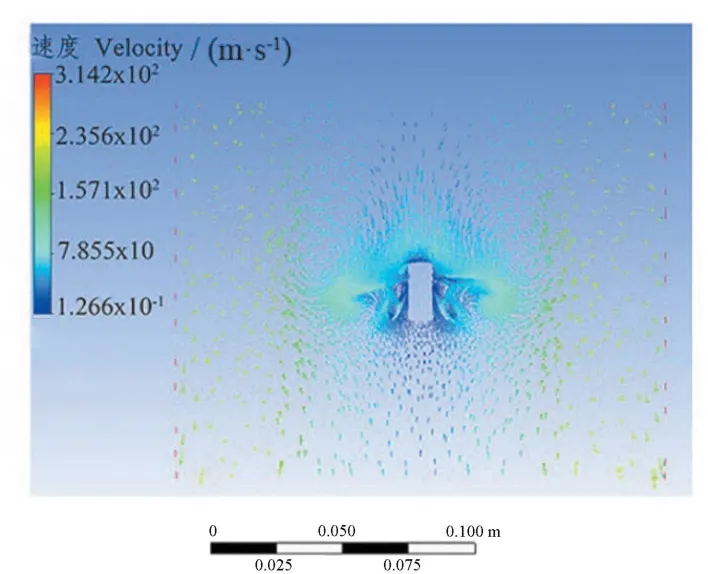
图11 优化后流速图 Fig.11 Flow rate diagram after optimization
4 优化后模型与传统斜叶片的对比模拟分析
相对比传统的斜叶涡轮叶片,优化后的双旋涡轮叶片,具有更高的效率,更好的流速图,为了直观形象地将结果进行对比,将模拟分析结果绘于图12、图13。

图12 传统斜叶流速图 Fig.12 Traditional flow velocity diagrams of oblique blades
由图12、图13 可知,对比优化后的模型与传统斜叶式模型叶片的流速矢量图与压力图得出,传统斜叶式涡轮叶片,会在中心轴的上端形成2 个不稳定的微弱的环流,叶片外流场2 侧的环流不明显;叶片在尾端存在高压区域,高压区域对叶片的使用寿命产生损伤。相对比优化后的双旋涡轮叶片,叶片与中心轴为全接触,改变中心轴底部空间的分布方式,使得中心轴底部的流体在流动时没有交错的阻隔,减少了乱流的发生,有明显的环流并且压力图中整体压力较均匀,无高压区,压力分布较合理,利于叶片运行及使用。综合上述图12、图13 的模拟分析,得出相较于传统的斜叶叶片,优化后的叶片压力分布更加均匀,环流较传统叶片更明显,搅拌效率更高。

图13 优化后流速图 Fig.13 Flow rate diagram after optimization
5 讨 论
本文通过贝塞尔曲线对叶片进行设计分析,通过对叶片数量、叶片有无开孔,中心轴有无开孔3 种参数的分析,得到了开孔对于双旋涡轮叶片的影响结果。对叶片数目为3、5、6 的双旋涡轮叶片进行了数值模拟分析,通过对比分析得出了6 叶片为最佳的叶片数目,叶片数超过6 片的情况不予考虑,这是因为双旋的叶片旋角在超过6 片时会发生干涉;对叶片开孔后的流场分布做了模拟分析,开孔后的流场由于孔洞带来的乱流,破坏了原本的循环环流,降低了搅拌效率;在对中心轴有无开孔的研究中,中心轴开孔后轴向的流动对整体的环流破坏较大,不利于搅拌效率的提高。循环环流的存在有利于提高搅拌效率,与文献[2]结论一致,文献[2]从搅拌器的自身特性分析,以循环环流的效果对比流场的特性,而本文以数值模拟分析与模拟得到此结果。通过综合分析影响外流场特性的参数来定性的分析外流场的分布情况。
文献关于搅拌器用涡轮叶片的研究,大多以单参数模拟分析,本文以对比分析为主,3 个参数综合考虑,对以上参数中开孔的情况进行了详细的模拟分析,得到在双旋涡轮叶片中叶片开孔、中心轴开孔不利于提高搅拌器的效率。整体来说,在开孔后出现了乱流,破坏了正常情况下的循环环流,降低了涡轮叶片的效率。在研究的双旋涡轮叶片中,6 叶片为最优叶片数目。正常情况下叶片数目应为奇数,但考虑到双旋叶片的旋角与叶片干涉的情况,6 叶片为最佳方案。
在流体机械的涡轮叶片研究中,叶片数目要根据叶片片型的实际情况而定。本文的分析在叶片数量、有无开孔等的情况中,分析的结果是受到多方面因素影响的。叶片开孔与中心轴开孔破坏了环流,降低了搅拌效率,不利于搅拌效率的提升。叶片的参数对于搅拌效率影响的判定,一直是热点与难点,缺乏量化的标准,后续将在参数影响因素对于效率的影响上进行量化方面的研究。
6 结 论
1)未开孔叶片相较于叶片开孔与中心轴开孔,压力分布更加均匀,双循环的环流更加明显,壁面处流速更加合理,提高了搅拌效率,增加了产能。在实际生产使用中要尽量避免不必要的开孔情况。
2)在分析的影响因素中,相较于叶片开孔与中心轴开孔,叶片数量对外流场的径向双循环环流影响最大,即对搅拌效率的提升影响最大。
3)中心轴开孔后,对轴向流体流动起到了微弱的额促进作用,但破坏了径向环流,大大减弱了搅拌效率,所以在实际生产中要避免轴开孔后的副作。
4)叶轮模型优化后,通过强化叶片与中心轴的接触方式与中心轴底部的空间分布方式,减少了乱流的产生,提高了搅拌效率。

