Elliptical model for surface topography prediction in five-axis flank milling

Liping WANG, Shuyi GE, Ho SI, Liwen GUAN,*, Feiyu DUAN,Yuzhe LIU

a Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China

b School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China

c Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China

KEYWORDS Cutter runout;Elliptical paths;Five-axis flank milling;Surface topography;Workpiece curvature

Abstract In five-axis flank milling operations, the intersecting surfaces of different cutting edges create roughness on the milled surfaces that cannot be ignored in situations with strict requirements,especially in aeronautical manufacturing. To focus on motion problems in milling operations, this paper presents a new model that utilizes elliptical paths as cutting edge trajectories on 3D surface topography machined by peripheral milling. First, the cutter parallel axis offset and location angle are considered,which change the location of the ellipse center and intersection point of the cutting edges. Then, through the proposed model, the predicted surface topography is obtained, and the factors that affect the development tendency of roughness are analyzed.Next,the effects of the cutter location position (CLP) geometric parameters, cutter parallel axis offset and curvature on the roughness are evaluated by a numerical simulation. Finally,machining tests are carried out to validate the model predictions, and the results show that the surface topography predictions correspond well with the experimental results.

1. Introduction

Aerospace products are representatives of the advanced manufacturing industry. Due to the continual changes in the requirements of modern aerospace products, more stringent requirements are placed on the processing quality and surface integrity of products. Currently, five-axis computer numerical control(CNC)milling machines are one of the most important processing tools for thin-walled aeronautical products.1

For aerospace products,non-developable ruled surfaces are widely used in product designs, such as aircraft wings and aero-engine blades. These products have features such as variable curvature, tilt, and distortion, and the five-axis CNC machine is the only effective machining tool to produce such features. In addition, the milling process is complicated, and the quality is difficult to guarantee with three-axis CNC milling machines. However, the accuracy of a five-axis CNC milling machine is always affected by multiple error sources,such as assembly error, system vibration and deformation,which directly affect the surface topography of products. The milled surface is defined as qualified product only when the errors are within a stated tolerance. The prediction of surface topography can discover the problems before the machining.Meanwhile, it also can be used to optimize the NC program and parameters, which can reduce production costs and effectively improve the processing efficiency and accuracy of complex products. Therefore, it is necessary to focus on the prediction of surface topography produced by five-axis CNC milling machines.To study the surface topography,a clarification is needed that the surface topography mainly originates from the cutting force and the forming principles of flank milling.The research about the first aspect is mature,in which the tool and workpiece vibrations caused by cutting force is the main source of surface topography.Hence,this paper is developed based on the second aspect,where the machining process is assumed to be rigid.

At present, most research concentrates on the surface topography generated by a three-axis CNC machine to improve the surface quality. Kıvak2developed a model with Taguchi method to optimize the surface roughness and the analysis of variance (ANOVA) was used to determine the effects of the machining parameters on surface roughness and flank wear. Based on tool center point methodology,Costes and Moreau3presented a model to predict the surface topography using tool displacements. The non-contact displacement sensors are used to record the vibration signal. A new iterative workpiece deformation prediction model is proposed for mirror-milling error prediction of low-rigidity parts.4Baek et al.5used a surface roughness model to analyze the effects of insert runout errors and variations in feedrate on surface roughness and dimensional accuracy in a face-milling operation. A theoretical generation model for a milled surface was established that considered the movement error of the principal axle.6The influence of back cutting on the surface finish obtained by face milling operations was studied.7Buj et al.8analyzed the effect of eccentricity and helix angle on roughness heterogeneity bands.Gao et al.9presented a method for the prediction of machined surface,based on the trajectory equations of the cutting edge relative to the workpiece and spindle runout was taken into account in three-axis milling operations. The effects of tool setting error, cutter geometry and feed on the band position,width and roughness were evaluated.10Li et al.11established a set of integrated information models to address the dynamics of machining conditions based on the dynamic feature concept proposed by the authors,which were used as the basis for integrating machining, monitoring,and online inspection operations for optimized machining process control of high-value complex parts. Based on analyzing the formation mechanism and characteristics of surface roughness, the machined surface roughness curve can be decoupled into kinematic surface roughness curve and stochastic surface roughness curve. The kinematic surface roughness curve is influenced by machining process, parameters and geometry of the cutting tool or wheel.12Methods have been developed to estimate the maximum radius of rotation and difference in the radii of rotation based on feature measurements on a machined artifact and acoustic emission signals during machining.13Arizmendi et al.14presented a model for the prediction of heterogeneity bands in the topography of surfaces machined by peripheral milling accounting for tool runout.Denkena et al.15presented a method for the reconstruction of surface topography of peripheral milled surfaces based on measured cutting forces. Buj-Corral et al.16developed a numerical model that predicted topography and surface roughness based on geometric tool-workpiece intersection. In this mothed, the surface topography was determined as a function of feed per tooth and radial depth of cut. However, five-axis milling has an advantage in the machining of complex ruled surface, due to the two more degree-of-freedoms than the three-axis machining.17And with the fixed cutter axis vector in three-axis machining, the coordinate system of the tool is parallel to the coordinate system of the workpiece in some modeling method,such as z-map, which is helpful to calculate the cutter-workpiece engagement. While the cutter axis vector varies with the cutter point position in five-axis flank milling,the geometrical relationship between two coordinate systems above keep variable, meaning that the model to predict the surface topography in five-axis flank milling is still a challenge issue.

Some studies with the five-axis ball-end milling, have been carried out in recent years.A simulation model for the prediction of machined surface patterns was developed based on the well-known N-buffer method as a function of the machining conditions.18Chen et al.19investigated the effects of tilt and lead angle on the surface topography in five-axis ball-end milling process,in which geometrical features of milled surface were analyzed. Prat et al.20presented a geometrical model of five-axis milling,which was used to determine the effective cutting conditions, the milling mode, and the cutter location point.Quintana et al.21studied the influences of the geometric characteristics of the theoretical surface roughness machined by ball end milling, in which the cutting parameters implication was analyzed on material removal rate (MRR) of ball end milling operations. Sonawane and Joshi22reported the effect of machining parameters on the quality of surface obtained in a single-pass of a ball-end milling cutter with varying chip cross-sectional area.Chen et al.23studied the influence of spindle errors on the frequency domain error formation of machined surfaces in ultra-precision fly cutting. Yao et al.24investigated the influence of tool and turning parameters on the surface integrity including the wear of inserts surface, cutting forces,and surface roughness.Nespor et al.25investigated the fundamental influence of cutting conditions and tool geometry on the surface topography after 5-axis ball nose end milling, and the tool runout were taken into consideration.Layegh and Lazoglu26presented a new analytical model to predict the topography and roughness of a machined surface in a five-axis ball-end milling operation by considering both the process parameters, such as the feedrate, flute number,step-over and cutting depth, and the effects of eccentricity and tool runout in five-axis ball-end milling. However, the ball-end milling has a lower productivity, because the manner of cutter-workpiece engagement (CWE) in this operation is point contact compared with line contact of flank milling. As for the machining process of non-developable ruled surface,only one cutting pass is needed by the five-axis flank milling with the cylindrical cutter. Due to the distinction between those operations, the models above are not acceptable to be applied in five-axis flank milling. Moreover, with the constantly decline of the magnitude of manufacturing precision,the geometrical features of workpiece in any practical operation can increasingly affects the surface topography.

Li et al.27derived the generation principle of surface morphology in five-axis flank milling, in which the surface morphology is taken shape combined with the entry angle and the exit angle of the tool. But with the increasing accuracy and quality of machined surface,the runout of tool causes significantly affection on the surface morphology. And the comparison of simulation and experiment should be considered to verify the model.

This paper proposes a prediction model of surface topography in five-axis flank milling based on elliptical paths of a nondevelopable ruled surface. The cutting tool axis vector, cutter position and runout of tool are taken as input information to the prediction model. The elliptical paths for the five-axis flank milling is derived which is helpful to the calculate the CWE, upon which the effects of the geometry of the cutter and curvature of the workpiece are analyzed. Finally, the model is validated through a comparison of the simulation results predicted by the model with the experimental results.

2. A surface generation model using elliptical paths in five-axis flank milling

In geometry, the flank milling in comprised of feed motion along the tool trajectory and rotation around the spindle axis.In the process of surface topography modeling, the envelope surface is generated by the combination of these two motions,wherein the cutting edges are involved in the removal of the workpiece.

It is known that the helical cutting edges are evenly distributed over the cutting tool, which can be treated as a cylinder,and angles exist between adjacent cutting edges in the tool geometry model.With a small radial depth,the angles lead to a situation in which the current cutting edge is not able to cut into the workpiece when the previous cutting edge is cut out of the workpiece; as a result of this phenomenon, a residual height is formed on the surface of the workpiece. Hence, the surface topography after machining is generated by the deviation between the actual profile and the ideal profile due to the residual height formed by the relative motion between the tool and workpiece, as shown in Fig. 1.

As a consequence, the surface topography is the intersection of envelope surfaces generated by each CLP. Before calculating all of the envelope surfaces, the tool becomes a series of discrete layers along the Z axis, and every crosssection is a unique ellipse with a distance which is equal to feed per tooth fz(fz= f/（nNt）) from the adjacent CLP,where f is feed rate, n is spindle speed and Ntis the number of teeth. Therefore, since the envelope surface of each CLP is one of the necessary parts to predict the surface topography, the definition of CLP to the elliptical paths would be first considered.

Fig. 1 Theoretical surface topography generation process in five-axis flank milling.

2.1. Position and tool axis vector of the CLP

Fig. 1 shows that the milled surface is formed by the residual height caused by the engagement of the cutting edges and the workpiece, of which the shape is mainly affected by the tool geometry and trajectories. Since the end mill is modelled as a cylinder with cutting edges on the surface, the CLP can be defined as the center point on the bottom of the cylinder,such as OTin Fig. 2(a), which is derived from the tool trajectories of the finished machining.

Due to features of non-developable ruled surface, such as variable curvature,tilt and distortion,the tool axis vector must continuously vary with CLPs. The tool axis vector and position are represented by six parameters［XD， YD， ZD， ID， JD， KD］ represented in Fig. 2(b), wherein the first three parameters represent the position and the last three represent the tool axis vector.

Meanwhile, in order to analyze the CWE, the assumptions are taken into account as followed:

(1) The workpiece and cutter are assumed to be rigid.

(2) The end mill, of which the part engaged with the workpiece,is discretized into i levels along the axis Z of workpiece coordinate system instead of the tool coordinate system.

(3) In the case that the tool axis vector parameters［ID， JD， KD］is equal to[0, 0,1], the tool is perpendicular to the workpiece

Since the tool axis vector is no longer fixed with respect to CLP in five-axis flank milling, the tool coordinate system varies with the tool axis vector,meaning that tool coordinate system of the current CLP is unparalleled to the previous one.The circular trajectory generated by one cutting edge at current CLP is non-coplanar with the one at previous CLP.

Thus, due to the complexity of spatial geometry, it is difficult to derive the intersection points between two adjacent CLPs by the circular path. So we assume the case that if the workpiece coordinate system is considered in priority,the tool axis vector is not perpendicular to the workpiece, and the cross-section of the tool at a certain height is converted from a circular shape to an elliptical shape, wherein two cylinder at two adjacent CLPs share the same cross-section with different elliptical shape.

Fig. 2 Tool geometry.

2.2. Cutter parallel axis offset and location angle

Ideally, the tool axis coincides with the spindle axis in which the theoretical tool radius is effective.However,due to assembly error of the tool in actual machining, the effective cutting radius would be influenced by cutter runout including the cutter parallel axis offset ρ and location angle φ, as shown in Fig. 2.

To describe the cutter parallel axis offset,a series of parameters, coordinate systems and planes are considered and the number of teeth is set to four. To be detailed, five coordinate systems are needed: the workpiece coordinate system XWYWZW, CLP coordinate system XPYPZP, spindle coordinate system XSYSZS,tool coordinate system XTYTZTand auxiliary coordinate system XEYEZE. First, the CLP system XPYPZPis obtained by a translation of workpiece system XWYWZWfrom point OWto point OPwith the distance provided by ［XD， YD， ZD］.

Then,axis ZPis rotated to coincide with the tool axis vector［ID， JD， KD］, and the spindle coordinate system XSYSZSis obtained in which axis ZScoincides with the spindle axis.Next,the cutter parallel axis offset ρ is determined by points A and B on axis XSand the location angle φ is determined by plane 1 and plane 2, whereas the tool system XTYTZTis obtained based on the runout parameters mentioned above. Finally,an auxiliary system XEYEZEis added at point OT, which is parallel to systemXWYWZW, as shown in Fig. 2(b). In Fig. 2(a), the cutter parallel axis offset is the distance between the spindle axis and tool axis in the spindle coordinate system.To relate the cutter parallel axis offset to the end mill cutting edges,the location angle φ between the X-axis in spindle coordinate system and the first cutting edge is considered.

It is obviously to find out that the actual radius requiring the engagement of cutting edge and workpiece is not the radius of cutter, but the distance between P1(or P2/ P3/ P4) which depends on the number of cutting edge) and spindle axis in the cross-section.The effective radius R（i，k）can be derived considering cutter runout as followed:

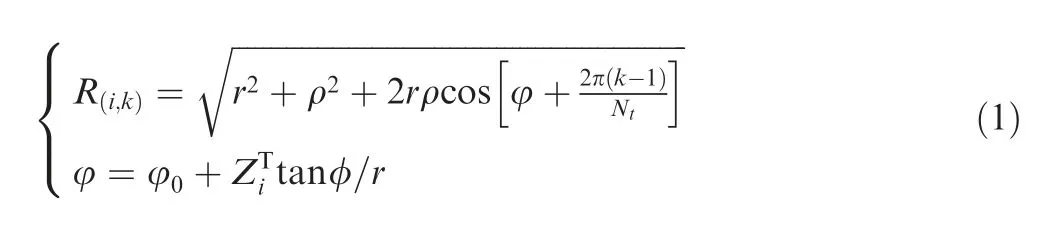
where k is the tooth number, as k=1，2，...，Nt; r is cutter radius;is the length of i-th level on z-axis in the system XTYTZT;φ0is the location angle when the height of point P is equal to 0; and φ is the helical angle of cutting tool.

Therefore, it is noticed that the actual trajectory generated by the cutting edges and the actual geometric parameters of the elliptical model would be greatly affected by the tool runout parameters.

2.3. Elliptical paths for cutting edge trajectories

Ideally, the tool axis coincides with the spindle axis in which the theoretical tool radius is effective. However, due to the assembly error of the tool in actual machining, the effective cutting radius would be influenced by the cutter parallel axis offset shown in Fig.2.In order to obtain the surface topography, the cutting edge trajectories should be focused on to describe the surface profile in each cross-section of discrete height. After the intersection points of adjacent cutting edge trajectories are calculated, the arc between intersection points to form the profile is carried out, which the groove is left to the workpiece. Gathering all the profile in each the crosssection at each discrete height, the surface topography is obtained through a discretization method.

As we mentioned previously, the circular paths result in complex spatial geometrical calculation of intersection points,where circles of two adjacent tool position are unable to appear on the same plane. Hence, the elliptical paths are presented to simplify the process to obtain the intersection points and profile, which are the necessary conditions for the surface topography.

To intuitively observe the geometrical characteristics of the cutting edge trajectories in the workpiece coordinate system XWYWZW,plane T and plane W are considered,which are parallel to plane XTYTZTand plane XWYWZW, respectively, in Fig. 3.

The spindle coordinate system is linked to the tool coordinate system by the runout parameters. The original point of the spindle moves along the X axis, and the moving distance is ρ. Thus, the center of the spindle does not coincide with the center of the circle; this results in a change in the effective cutting radius. The effective cutting radius of the cutting edge increases as the distance from the center of the spindle increases, whereas the effective cutting radius of the cutting edge decreases when the position draws nearer to the center of the spindle.

Fig. 3 Elliptical trajectories.

Without considering the variation of cutter axis vector,the feed motion can be transformed into cylinders of different radii that repeat with a period equal to the feed per tooth fzand move along the feed direction in Fig. 4(a). The effect mentioned above can be illustrated as shown in Fig. 4(b). Due to the variation of tool axis vector, it is needed to introduce a new parameter β（i，k）should be considered,which is the rotation angle between the direction of the major axis and X axis of the spindle coordinate system.

Meanwhile, the number of teeth generating the profile should be considered in the model. It is divided into two aspects—radial cutting depth aeand effective cutting radius,as shown in Fig. 5.

The outside surface of cutting tool is extended along the circumference,as shown in Fig.5(a),where the red line represents the central line of a certain cutting point.It can be seen that the surface profile of this area is generated by tooth 1, 2 and 3 at different height, respectively. Hence, the cutting tool can be divided into three parts according to the height: (1) when h2hc,the current tooth is tooth 1. And hcrepresents the limited height for a cutting point which is only swept by one cutting edge. Therefore, the number of teeth generating surface profile depends on the relationship between axial cutting depth and hc.

To illustrate the number of tooth generating surface profile determined by the effective cutting radius,a 3D surface topography is shown in Fig. 5(b) that profile generation is transformed form tooth 3 to tooth 2. To be detail, due to the consideration of cutter runout in the simulation, the cutting radii of each cutting edge are different from each other,which results in the variation of tooth number generating the surface profile.

2.4. The surface generation model for five-axis flank milling

First, in system XWYWZW, the cross-sectional shape is influenced by the tool axis vector,and the rotation angle β between the axis of the elliptical model and the X axis is determined.Then, the center of the elliptical model varies with the height and tool axis vector, whereas the distance to the adjacent ellipse center is fz. Finally, according to the tool axis vector and the effective cutting radius with runout parameter, the major axis and the minor axis length of the elliptical model can be obtained. Through the steps above, the geometric parameters of the elliptical model are obtained, as shown in Fig. 6.

Fig. 4 Cross-section.

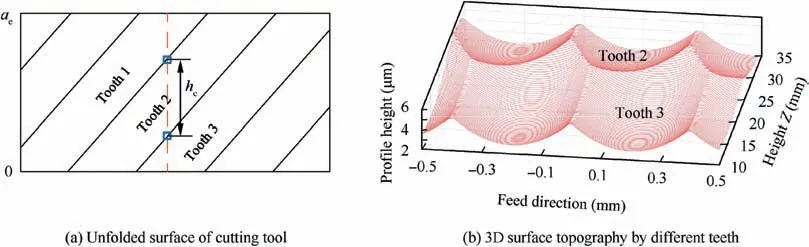
Fig. 5 Teeth number for generating the profile.

Fig. 6 Elliptical model parameters.

In Fig.6,the length of the major axis and minor axis of the elliptical model is limited by the tool axis vector and the tool runout parameters. The position of the elliptical model is defined by the tool axis vector and the position. In addition,the rotation angle β is also controlled by the tool axis vector.As consequent, the geometrical parameters of the ellipse are shown in Eq. (2).

where a（i，k）and b（i，k）represent the major axis and the minor axis of the ellipse model, respectively; the rotation angle β is between the direction of the major axis and X axis of the spindle coordinate system; and tilt angle α is between the tool axis vector and Z-axis of the workpiece coordinate system.

Once the elliptical expression of point P（i，k）(a point located on a cutting edge,such as P1)is derived,the position could be transformed to the coordinate values in coordinate system XEYEZEthrough the standard equation of ellipse:

However, the standard equation of ellipse is limited by the following conditions: (1) The geometrical center is original point of the current coordinate system, which is represented as(0,0),fastening the position of the ellipse.(2)The major axis of ellipse coincides with axis X of the current coordinate system, meaning that the rotation of the ellipse is fixed.

The Eq. (3) only provides the detailed size to describe the cutting paths at height of,without position and pose,which causes calculation error for intersect points. In order to complete this model, the transformation matrixWTEis defined to map the given vectors from the coordinate system XEYEZEto the coordinate system XWYWZW, which can be written as:

represent the values of the ordinate of the elliptical center at a height ofin system XWYWZW.xW,yWand zWcorrespond to the values of the ordinate of point on the current ellipse.As the inputs of position and tool axis vector are given,the elliptical paths can be derived considering the cutter runout.Since the intersection points can be calculated with respect to the adjacent CLPs,the surface topography,gathering the profile of left grooves by cutting edge trajectories at a discrete height, is studied. Moreover, the surface topography based on the elliptical model can be predicted in a short time. With a normal computer,the calculation time of the roughness profile at a certain height, for a standard ‘S’ test piece with 2220 CLPs, is within one minute.

2.5. Evaluation for the surface topography

The surface topography is composed of elliptical arcs by the cutting edge trajectories, which is difficult to figure out the integral change trend, and hence, the evaluation process to depict the surface topography is essential. Surface roughness is chosen to evaluate the surface topography, which include the arithmetical mean deviation of the profile (Ra), average height of irregular ten points(Rz)and maximum height of profile (Rt). The calculation for Rais executed depending on the datum line by which the profile is divided into two portion of equal area, whereas the difficulty in computation is obviously increased. As for the calculation of Rtis simple, but value of Rtis greatly affected by the random cause.The expressions for calculating these roughness parameters are written as followed:

where m is the sampling number, and Z（x） represents the distance between datum line of profile and sampling point.Zp（x）and Zv（x） are the largest length of profile peak and valley,respectively. Zpmaxand Zvmaxcorrespond to the maximum height of peak and the maximum depth of valley respectively.

As a consequence, Rzis selected to evaluate the surface,which is a relatively simple but comprehensive computation method compared to Raand Rt. According to the elliptical model with the input of CLP, the values of the ordinate of the profile can be obtained by the means of derivation of intersection points. Combining the Eq. (5) with the position of the profile, the evaluation parameter Rzcan be calculated.

2.6. Error made in the approximation of elliptical path and cycloid path

In order to obtain the surface topography, the simulation of teeth trajectories at each CLP should be required.This simulation involves with calculation of point positions of each cutting edge. Moreover,the profile depends on the intersection points by cutting edges.Once the profile at each height is determined,the surface topography can be formed by gathering all profiles.

Fig. 7 Cycloid path vs elliptical path.

For the sake of simplification, the cycloid path that generate the profile is approximated to the elliptical path, as shown in Fig. 7(a) and (b). One segment of cycloid path can be substituted for several ellipses located with the same distance equal to feed per tooth fz, which lead to an error made in this approximation. This approximation error is calculated by the difference of Hresbetween the cycloid path and the elliptical path. And Hresrepresents the residual height on the surface.There is a need to figure out the detailed approximation error due to the accuracy problem of this model.

Fig. 7(c) and (d) show that the error made in this approximation can be ignored. Meanwhile, the figures reflect the change rule of residual height and approximation error which vary with the dimensionless parameter fz/r. Hence, the accuracy of model can be ensured when the actual trajectory is approximated to the elliptical path in the simulation, which also improves the calculation efficiency.

3. Analysis of the main factors that affect surface topography

As the theory is presented above,the surface generation situation is obtained according to cutting edges trajectories. It is obvious that the surface topography is closely connected with the tool geometry and cutting edge path.To illustrate the influences of both, it is helpful to consider a particular case. For example, consider the cutting conditions in Table 1. The location angle φ has can vary from 0° to 90° with the position offirst cutting edge.And φ varies at different heights due to helix angle.In addition,the variation in the surface topography can be caused by the tooth number.

Table 1 Simulated cutting conditions.

3.1. Influence of cutter axis offset ρ on effective cutting length

Due to the existence of a helix angle, the position of the point ρ（i，k）on the cutting edges continually changes,which results in a variation in the location angle φ with respect to the discrete height. To illustrate the influences, it is helpful to consider a particular location angle φ0; for example, consider a value of φ at the height of Z0in coordinate system XTYTZT. Then,let us consider the plane T, which is perpendicular to the tool axis vector. From the perspective of plane T in Fig. 8(a), it is helpful to figure out the relationship between the tool runout and effective cutting radius, by which it can be analyzed that the order of teeth generating the surface depends on the cutter parallel axis offset.In addition, a tooth path could be covered by others without generation the profile at a certain value of cutter parallel axis offset.Thus,the situation of each teeth generating the surface should be firstly discussed to ensure the calculation of intersection points at a heightAs shown in Fig. 8(b), the effective cutting radius of each cutting edge varies with respect to the cutter parallel offset ρ in system XTYTZT, which provides the foundation for the variation between the value of ρ and the effective cutting length:

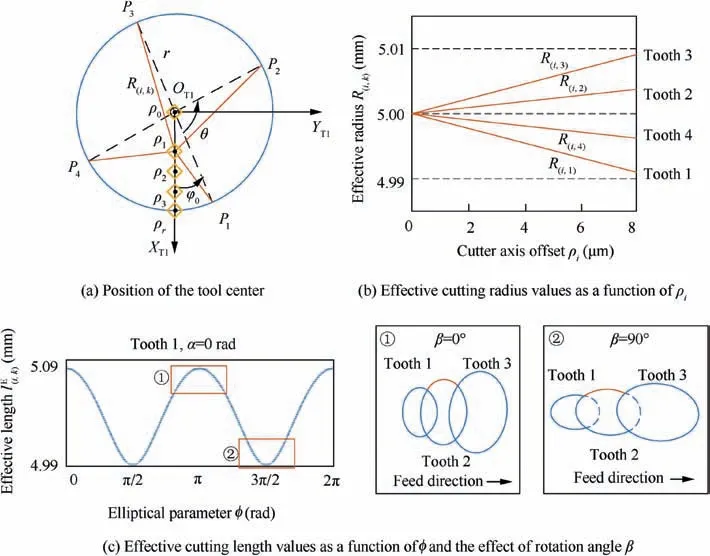
Fig. 8 Influences of cutter parallel axis offset.

The distance shown in Eq. (6) from each point on the trajectory to the center is different in the elliptical model, which depends on the rotation angle β.Let us compare the situations where β=0°and β=90°. Between these cases, the intersection point position of adjacent cutting edges changes from the long axis to the short axis, which obviously indicates that the rotation angle β can directly affect the effective cutting lengthin Fig. 8(c).

3.2. Influence of workpiece curvature on surface topography

The groove generated by the current cutting edge at the heightdepends on the distance between two intersection points,which involve with ellipse models of three adjacent cutting edges (the previous one, the current one and the latter one).We convert this mathematic calculation to the practical machining. The origin of this groove represents the position,which the tooth cut into the workpiece.Similarly,the terminal point defines the position, which the tooth actually cut out of workpiece.

Therefore, the surface topography is determined by cut-in/cut-out characteristics of the cutting edges, which means that the surface can be directly affected by the relative motion between the tool and workpiece.

Due to the features of non-developable ruled surfaces in five-axis flank milling,it is common to find the form of relative motion varying with time.In the situation where the tool trace is a straight line and the change in the tool axis vector is neglected, the cut-in/cut-out of two adjacent cutting edges remains consistent. In the situation where the tool trace is a convex arc and the change in the tool axis vector is neglected,the cut-in of the previous cutting edge and the cut-out of the latter cutting edge are advanced with respect to the linear trace. In the situation where the tool trace is a concave arc and the change in the tool axis vector is neglected, the cutout of the previous cutting edge and the cut-in of the latter cutting edge are lagged with respect to the linear trace in Fig.9(b).In the case of leading,the cutting time and engagement region of the cutting edges and workpiece are reduced.In contrast,in the case of lagging,the cutting time and engagement region of the cutting edges and workpiece are increased. In the elliptical model, the cutting time can be replaced by φ in the elliptical equation, which directly influences the effective cutting length

Fig. 9 Relationship between the curvature and surface topography.

Comparing the lengths d1，d2，d3, which represent the residual heights of some points in Fig. 9(a), the effective cutting lengthdecreases when the cut-in/cut-out is leading during the convex trace process. In contrast, the effective cutting lengthincreases when the cut-in/cut-out lags during the process of concave trace. These two trends shown in Fig. 9(d) display the relationship between curvature and surface topography.

3.3. Influence of the tool axis vector on the surface topography

The tool axis vector shown in Fig. 10(a) is an important motion feature in five-axis milling, especially for the nondevelopable ruled surface machining. Simultaneously, it is one of the input information in the predictions of surface topography in five-axis flank milling (Fig. 6). Hence, it is necessary to analyze the effect of the tool axis vector on the surface topography.

According to Eq.(1)and Fig.6,the rotation angle β and tilt angle α are influenced by the tool axis vector［ID， JD， KD］.The rotation angle β has an influence on the effective cutting lengthby changing the situation of cut-out in Fig.10(b).On other hand,the tilt angle α has an influence on the major axis length a（i，k）, as shown in Fig. 10(c).

Fig. 10(b) shows that each segment arc extracted form CWE on the cross-section is unique, due to the geometrical features of the elliptical shape.The rotation angle β influences the intersection segment by changing the situation of cut-out during the machining process. For example, in the case that β is equal to 0, the intersection segment, which is generated by the current cutting edge and the two adjacent cutting edges,is close to the elliptical short axis.In the case that β is equal to 90°,the intersection segment is located on the major axis of the ellipse. By comparing two intersection segments, it can be found out that the effective cutting lengthwhen β is equal to 0 is smaller than that when β is equal to 90°.

It can be observed in Fig. 10(c, d), the major axis length a（i，k）of elliptical model increases with increasing tilt angle α,whereas the value of KDdecreases with increasing tilt angle α; KDrepresents the degree that the tool axis vector deviates from the Z-axis.However,the value of tilt angle α is very small in machining process;therefore,the value range in Fig.10(d)is inappropriate.For the actual situation,a similar trend of local variables can be found,even though the variation in major axis length a（i，k）is slightly affected by the tilt angle α, which is less than one degree.

4. Simulation and experimental validation

4.1. Experimental design

To validate the established surface topography model, the machining experiments were conducted and the comparison between the predicted surface (roughness) and measured surface is the main evidence. The experiments are performed on a five-axis milling machining center DMU 60 MONOBLOCK in Fig. 11.

With the small machining parameters, the cutting could be assumed to be rigid without dynamic effects and chattering effects.28,29The spindle speed was 1000 r/min, the feedrate was 200 mm/min, the radial cutting depth was 0.8 mm, and the axial cutting depth was 5 mm.Aluminum alloy 7075,which is commonly used in aerospace manufacturing,was selected as the workpiece material.A two-tooth cemented carbide flat-end cutter with a 16-mm diameter and a helix angle of 45 was used.Before the machining tests,the runout parameters are obtained measuring the circle around the tool by the dial indicator when the tool is put into the toolholder. In addition, after measurement, the two runout parameters for the current cutter can be obtained, where cutter parallel axis offset ρ = 0.005 mm and location angle φ = 30°.

Fig. 10 Relationship between tool axis vector and surface topography.

Fig. 11 Machining process.

For the comparison of predicted surface to machined one,a surface profiler(Form Talysurf I-120 in Fig.12)was utilized to measure the roughness of the milled surface to evaluate the surface topography,which include the arithmetical mean deviation of the profile Ra,average height of irregular ten points Rzand maximum height of profile Rt. In order to be rigorous in the measurement,the roughness value of each area is measured at three different heights to obtain an average as the final measurement result.

Fig. 12 Measurement process.

To emphasize the feature of five-axis machining process, a typical workpiece featured in the non-developable ruled surface was designed for model validation, as shown in Fig. 13(a). This designed specimen is composed of two similar ruled faces, each of which is defined by a set of generatrix and two B-spline curves.30,31Due to the features of non-developable ruled surface,the shape of specimen,as a combination of plane surface and cylindrical surface with variable radius, has variable curvature.

Fig. 13 Machined surface of the test specimen.

Considering the machining features of the designed specimen, it is helpful to machine one side of the specimen to decrease the deformation. Therefore, the red curved surface in Fig. 13(a) was chosen to be analyzed. In Fig. 13(b), the detailed control points which are used to generate the Non-Uniform Rational B-Splines (NURBS) curves including line A and line B are listed in Table 2.

4.2. Results analysis and discussion

First,surface roughness parameters are selected to evaluate the surface topography with Ra, Rzand Rt. Then, the surface is evaluated by Rzin the simulation shown in Fig.14(a).Finally,due to the curvature of workpiece, 9 areas are chosen to be measured to represent the actual surface topography in Fig. 14(b), and the measurement data are listed in Table 3.The areas ②, ③, ④is concave trace, the areas ⑥, ⑦, ⑧is convex trace, and the areas ①, ⑤, ⑨is linear trace which are the main distinction in the machining process. Fig. 14(a)mainly shows the roughness variation caused by workpiece curvature, and the effect of cutter runout cannot be reflected in this figure.

Then,the area ⑨where the curvature is approximate to 0 is used for simulation of 3D surface topography to display the effect of cutter runout.And the surface topographies with cutter runout and without cutter runout are shown in Fig. 14(c)and (d), respectively. By the comparison of the surface topographies, it can be validated that the effect of cutter runout on the surface topography is very complex. Moreover,the actual surface topography of areas with convex trace,concave trace and linear trace are drawn in Fig.15 during the measurement process.

Through analysis of the simulation and measurement validation, the model proposed in this paper can be validated as follows:

The data in Table 3 are sorted by size (maximum to minimum): ②＞④＞③＞①≈⑤≈⑨＞⑦＞⑥＞⑧. The sorting of the sizes coincides with the curvature of the corresponding area. Thus, a positive correlation was found between the curvature of the workpiece and roughness.

To compare the situation of the actual convex and concave trace, the roughness data Raof ②, ⑨and ⑧are used to calculate the residual height ratio.The residual height ratio of ②is 245.95%,whereas the value of ⑧is 79.47%,which is similar to the prediction in Fig. 9(d).

Due to the prediction model without considering vibration and tool wear, the simulated roughness Rz（S） is less than the measured roughness Rz（M）. However, it is important to find out that the developing trend in the simulation coincides with the measured trend, as shown in Fig. 16. To illustrate this problem,the deviation errors formed by the simulation results and experimental ones are plotted in Fig.17 and the expression for deviation errors is written in Eq. (7).

Table 2 Positions of the control points.

Fig. 14 Prediction simulation of the surface topography.

Table 3 Measured roughness data.

where Ra（M）, Rz（M） and Rt（M） are the measured roughness data and Rz（S） is the simulated roughness data.

These experiments verify that the proposed surface generation model can predict machining surface topography by using elliptical paths. Moreover, a positive correlation between the roughness and curvature exists. Surface topography simulations have important implications for reducing roughness and improving the quality of workpiece and machining.

5. Conclusions and future work

This paper presents a model for the prediction of surface topography in five-axis flank milling, taking the tool runout into account, wherein elliptical paths are utilized as cutting edge trajectories. With the model, the influence of the runout,curvature of the workpiece and the tool axis vector to the surface topography is analyzed and it can be drawn that:

1. Taken as the input information of CLPs, the algorithm for the ordinate value of points in elliptical model is proposed.Once the elliptical trajectories are obtained, the surface topography depending on the discrete density of height can be studied.

2. The runout parameters including cutter parallel axis offset and location angle have a great effect on the effective cutting length, which influence the profile generated by the tooth path. Meanwhile, the tool axis vector also affects the effective cutting length by the means of the rotation angle β and tilt angle α.

3. Through a design specimen of non-developable ruled surface, a positive correlation between the roughness and curvature is discovered in the experimental test with a constant feed, wherein the roughness is used to evaluate the surface topography.

4. The model in this paper was proved by the comparison between the predicted surface roughness and the measured one obtained in the experiment.A good agreement between the results was found with deviation in ranging from-2.81% to 20.1%.

The model can be extended in the future work combined with the tool vibration and feed. Based on the relationship between curvature of workpiece and roughness,the adjustment of federate can be modelled in the follow-up research to obtain a smooth surface which is benefit to improve the quality in machining.

Fig. 15 Actual surface topography during measurement.

Fig. 16 Comparison between the simulated and measured results.

Fig. 17 Deviation errors between simulation and experiment.

Acknowledgments

This research was financially supported by the Major National S&T Program of China (2017ZX04002001), the Major National S&T Program of China (2016ZX04004004) and the National Natural Science Foundation of China (51675301).