An energy-based coupling degradation propagation model and its application to aviation actuationsystem

Tongyng LI, Shoping WANG, Jin SHI,*, Enrico ZIO, Xioyu CUI

a School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China

b Energy Department, Politecnico di Milano, Via La Masa 34, Milano 20156 , Italy

c MINES ParisTech, PSL Research University, CRC, Sophia Antipolis, 06410, France

d Department of Nuclear Engineering, College of Engineering, Kyung Hee University, Gyeonggi-do 12001, South Korea

KEYWORDS Actuation system;Cascading failure;Complex system;Failure propagation;Mechatronic system

Abstract The degradation of components in complex mechatronic systems involves multiple physical processes which will cause coupling interactions among nodes in the system.The interaction of nodes may be carried out not only by physical connections but also by the environment which cannot be described by single network using the traditional methods. In order to give out a unified model to quantitatively describe the coupling degradation spreading by both physical connections and environment, a novel Energy-Flow-Field Network(EFFN) and a coupling degradation model based on EFFN are proposed in this paper.The EFFN is driven by energy flow and the state transition of spatially related nodes is triggered by the dissipation energy. An application is conducted on aviation actuation system in which the degradation spreading by fluid-thermal-solid interaction is considered. The degradation path and the most probable fault reason can be obtained by combining the state transition and energy output of nodes, which is consistent with the given scenario.

1. Introduction

Systems such as production system in modern process industry, power supplying system of a high-speed train1and actuation system in an aircraft2are complex mechatronic systems which involve multiple physical processes including mechanics,electrics and hydro-mechanics. With growing complexity, an increasing interaction among components inevitably brings about threat of cascading failures in mechatronic systems,which has become a key focus currently.3-6

Taking the topological perspective,the complex connecting relation of mechatronic components can be described as complex networks. The most famous complex networks are small world network and scale-free network. Watts and Strogatz proposed the small world network in which the connection topology is neither completely regular nor completely random.7Based on the small world network, Gao et al.8studied the fault propagation of a production system. Barabasi and Albert proposed the scale-free network9in which new nodes can be added into the network and attached to the nodes which are already well connected. The two networks solved the increasing topological complexity by extending networks with arbitrary connections and scales.

The cascading failure ordinarily starts from the malfunction of a single component caused by a random trigger,which propagates along spreading paths and finally results in a catastrophic impact on the holistic system. Overload may occur on both nodes and edges and is believed as the main causes in many real cases. Ren et al.10focused on the effect of load distribution law on the power grid which is regarded as a complex network with generators, substations and consumers. Wei et al.11analyzed the cascading failure faults in transmission networks combining complex network theory with cascading faults graphs. Jing and Tang12evaluated the effect of cascading failure considering the characteristics of time delay and recovery strategy.Lin et al.13,14assessed the reliability of complex electromechanical system using complex network method.There are also research studies concerning the cascading overload failures caused by network load dynamics. Zhang et al.15established a probabilistic cascade failure model using mean field theory and impact of initial load and tolerance parameter distribution on cascade failure was investigated. Zhang and Yag˘an16analyzed the load dynamic in electrical power systems and the robustness was optimized.

It has been identified that cascading failures in real-world systems are also caused by interdependency among components. There are various failure modes for different mechatronic components, i.e., failure modes of an aviation hydraulic pump involve bearing failure, internal friction wear,piston head gap increase and swash plate incline17,18. Most of the failure modes are not independent like the internal friction wear which may also be intensified by higher working pressure caused by other components in the system.Liu et al.19utilized the node-coupling strength to describe the dependency between nodes and the percolation framework was used to study the robustness of the networks. There are also research studies concerning the interdependency among different networks. Based on percolation theory, Su et al.20analyzed cascading failures on interdependent networks using multiple dependency links and cliques. Zhong et al.21investigated the restoration of interdependent network after cascading overload failure using a load-dependent cascading model. Liu et al.22studied the percolation in coupled networks considering both inner-dependency and inter-dependency.

The relation of components in mechatronic systems is jointly affected by load dynamics and dependency among components. Probably, in an aviation actuation system, an accident starts from a initially slight fault on a component like an actuator clamping, and then, the motor connected to the actuator is blocked and generates more heat which rises the operating temperature and finally leads to a systematic failure.2In this scenario, failure spreads from actuator to motor by physical links, from motor to other part of the system by environment. Similar impacts of environment may be carried out by vibrations and electromagnetic fields.23These complicated spreading paths display a cumulative characteristic and attenuate with spatial distance of the components.24In this paper, overload on a single component is believed to be the start point in a cascading failure, while the block of a motor may not cause a shock failure, but a gradual degradation instead, which means that the influence on the other components in mechatronic system begins when the working condition changes.

Based on the aforementioned methods, the overload spreading along physical connections and the influence spreading by environment can be regarded as two interdependent networks. Since the interaction of multiple physical processes is complex in mechatronic systems, it is difficult to define the load-dependent relation between the two networks. Aimed at giving out a unified model to quantitatively describe the coupling degradation spreading by both physical connections and environment, this paper proposes a universal Energy-Flow-Field Network (EFFN). In EFFN, components are nodes with energy capacities and spatial structure linked by edges with strength and length. Changing the state of a node will conduct a physical impact on the connected nodes and an accumulative field impact on the nodes closed in space dimension, which means that degradation propagates along both physical links and temperature or electromagnetic field.A certain capacity degradation of a node according to the degradation mode and its corresponding severe degree will have a coupling effect on the related nodes which is described as a coupling degradation coefficient matrix in this work. The propagation paths solving of the proposed network follows the framework of stochastic flow network25-28by using the concept of minimal paths and minimal cuts.

The rest of the paper is organized as follows: in Section 2,the problem is described in detail and some basic assumptions are proposed. Section 3 introduces the novel EFFN and the degradation propagation and coupling model based on the network. In Section 4, the application of the model to an aviation actuation system is presented. Conclusions are drawn in Section 5.

2. Problem description and assumptions

In traditional networks, when the load on a node exceeds its capacity, the node fails. The load is the measurement of the flow and the flow can only be transferred by edges, which reflects most normal working operation of complex systems.When degradation occurs, nodes connected to the degraded node may be also influenced and perform a lower working efficiency such as a higher congestion rate of a connected traffic intersection, a higher delay rate of a connected information point, a lower operating voltage of a connected substation and a lower working pressure of a connected pump.The degradation of nodes can be described by multistate models like stochastic flow network. For a mechatronic system, energy works as the medium flowing with different forms and the devices work as nodes transforming and transferring energy in the network.During the transforming and transferring process, it also generates heating and vibration which are triggers of degradation of other components. The influence between two components without physical connection is recognized as field effects in this paper, and meanwhile the influence of a connected component is the flow effect.

In terms of energy,the components,devices and subsystems which are regarded as nodes in a network are points with input and output energy which converse energy among different types or transfer energy under some rules. The connections are the paths for energy transferring. Generally, energy exists in different types. In this paper, the kinetic energy, internal energy and electrical energy which flow on physical connections are named flow energy, and meanwhile, the informational energy, thermal energy, luminous energy and magnetic energy which mainly spread by the environment or other systems are regarded as field energy. Note that the definition is not unmitigated but should be determined by the actual transferring paths in a certain network. Differentiating from flow energy, field energy usually has an accumulative effect on the components in the environment. The amount of field energy on a certain component may be small but a continuous degradation threat grows with the rising of field intensity. For definiteness and without loss of generality, the original flow is redefined as the physical transfer path of energy. According to the conservation of energy, in mechatronic systems, energy will never disappear but transfer among components and environment.The proposed energy-flow-field system is assumed to satisfy the following assumptions:

(1) Energy transfer from one component to another by flow

and field.

(2) Every component obeys the law of conservation of energy,while the input energy transferred by field is very small compared to the energy transferred by flow which can be neglected but can be regarded as the trigger of influence.(3) The field energy dissipates into the local environment or other systems and gradually permeates into global environment or other systems.

3. Modeling of degradation propagation and coupling

3.1. Energy-flow-field network (EFFN)

EFFN is described by nodes and edges.Each network has only one source node.As is shown in Fig.1,a generic node receives energy φ（in）（t） by flow and gives out energy φ（out）（t）. Meanwhile, a part of energy ψ（out）（t） is dissipated in forms of field energy from the node. Energy ψ（in）（t） dissipated from other nodes are transferred by field edges into the node. Solid lines are the paths for flow and dashed lines are the paths for field.c（t） stands for the capacity of the node and c（0） is the rated capacity. w is the inherent energy loss consumed by the node itself and η（t） is the efficiency of the node defined by

η（0） is the rated efficiency. According to the conservation of energy,

A source node generates energyand does not influence other nodes or is not influenced by the field. For a sink node, energyis consumed by the node itself, and meanwhile the node may still influence other nodes and the lowest required energy of node is wt（0）. The energy balance can be described as

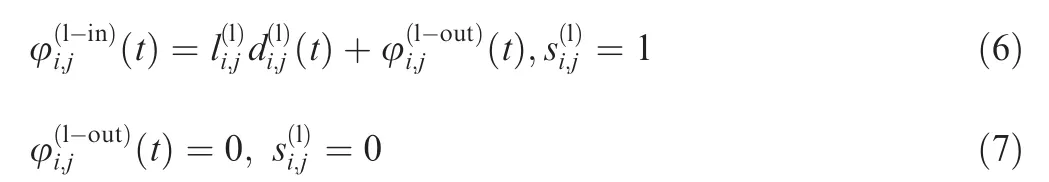
Fig. 1 Node models in EFFN.

Table 3 Influence coefficient of different nodes.

Table 4 Equivalent average energy demand of a controlled surface.

For real aircraft,the energy is not transferred stochastically in the network. The nodes are controlled by flight plan,which means that the energy demands are determined by the terminal users29. An equivalent average energy demand of a controlled surface in each flight phase is shown in Table 4.

Table 6 Node data of Fig. 4.

Commonly,there is no physical isolation change during the system running, so the field edges are believed to be reliable.To simplify the problem, the dimensionless dissipation rate of each flow edge is set to be 0.1 and the corresponding lengthsof flow edges and field edges are shown in Table 5.By supposing that the same kind of nodes have individual differences,the node data are shown in Table 6.

Table 5 Edge data of Fig.4.

Fig. 5 Degradation states of nodes.

Fig. 6 Field output energy of nodes.

Fig. 7 Field input energy of nodes.

In order to demonstrate the propagation scenario instead of an actual life-cycle degradation of the system, the transition probabilities shown in Table 3 are given much higher values in the simulation than the real situation so that the propagation will not last too long and the capacities of nodes are close to the emergency stage so that the nodes are inherently vulnerable. Assume that each node works under rated condition in the beginning,and at the emergency stage,the motor of EHAS at left middle aileron degrades to the slight fault state firstly.Fig. 5 shows the results from a single simulation. We can see that the transition of degradation states of each node presents the degradation propagation path: the motor of EHAS at left middle aileron v6degrades, afterwards the pump v7connected to it degrades and then the cylinder v8transfers to a severe fault state. The other nodes degrade as shown in the figure,and the figure is one single simulation result that some of the nodes do not degrade by the effect of flow and field, which degrades by its autologous degradation instead of the propagation from other nodes. The node then becomes another starting point of degradation propagation.

Fig. 8 Total dissipation energy.

Fig. 9 Dissipation energy of each step.

Both flow and field energy may cause the degradation.Fig. 6 shows the field output energy of the actuation system on the left middle aileron,which helps to analyze the degradation reasons.At the second time step,an overload is applied on node v6. The motor v6transfers to the slight fault state at the fourth time step,which leads to a slight overload on the motor and more energy dissipation to the field.There is no increase in field output energy of node v7which connects to v6by field edge and no state change of nodes v5and v7which connect to v6by flow edges. Thus, the degradation of v6at the fourth time step to a severe fault state is caused by the overload on itself. The second degradation of the system happens on node at the seventh time step at the seventh time step. The output field energy of v6is 18.0889 when node v7degrades, and from Fig. 7, we can see that, after several time steps, the accumulative input energy on v7by field reaches 17. The influencing intensity of energy by v6is higher than w7and a high level influence coefficient CDCM6，7（Ihigh） shown in Table 3 is applied.Because v7is at normal state before state transferring,according to Table 2, the autologous degradation probability from normal to severe fault is zero. Then we can confirm that the degradation is caused by v6. Otherwise, the autologous degradation possibility may also be considered.

The total dissipation energy by field is shown in Fig.8.The slope of the energy curve is small at first,which means that less overloads happen and most nodes of the system are at normal states. While the degradation occurs, the slope becomes larger and larger, which can also be seen in Fig. 9. We can find that,from time step 70,the slope remains a constant until time step 160. Compared to Fig. 5, most nodes already fail before time step 70, which means that most nodes stop working and the field energy is generated by minor nodes v2and v5. Node v2finally fails because of long time overload and gives rise to a dramatic decrease on the slope.The slope then remains a constant until the simulation stops.

Fig. 10 Dynamic failure process of system with dependent components.

Fig. 11 Dynamic failure process of system.

Since the degradation of components is modeled as a stochastic state transition process, the inherent uncertain should be considered.A Monte-Carlo simulation is conducted on the actuation system and the statistical results are obtained.By setting different initial degradation states,the dynamic failure process of the system is shown in Fig.10.Each result is the accumulation of 1000 realizations.Fig.10(a)shows the results when the initial degradation state of each node is slight fault,from which we can see that, in such situation, the failure processes triggered by different slight faults are with little difference. When the initial degradation state of each node is severe fault, more difference can be found, that is, the system statistically arrives at a more severe failure state,which can be explained by the difference of state transition rate under low efficiency and high efficiency.Node v2affects the system most,which is consistent with the given scenario. Meanwhile, node v3and node v6cause more impacts than node v4, node v7and node v8because of the load dynamics and topology.

Fig. 12 Comparison of capacity-load model and EFFN.

By setting all the elements in CDCM to be ones,the system is transferred to a system with independent components,which means that the degradation of the system is determined by the dynamic loads completely. The dynamic loads affect the system with independent components by ADR.With higher loads or lower efficiency, the independent components are more likely to degrade. The comparative results are shown in Fig.11 By neglecting the influence of dependency among components, the number of failure nodes decreases sharply compared with the dependent components. Meanwhile, the difference between the influence of initial severe states and initial slight states becomes larger.The initial severe state of node v2has a greater impact on the system.

To make a comparison with the traditional methods, we consider a static model using capacity-load analysis which is a commonly used method to analyze the cascading failures.The capacity-load model30considered that the capacity of network node is constrained by cost, and assumed a linear relationship between the capacity and load of nodes. Combined with the concept of capacity-load model, the capacity of each node is defined the same as EFFN, which is listed in Table 6.Cascades are assumed to be triggered by the removal of single nodes.The comparative results are shown in Fig.12.From the figure,we can see that since the capacity-load model is a static model which cannot reflect the degradation process of each component, the number of failure nodes reaches the steady state within a very short time. The result of capacity-load model actually does not concern the uncertainty caused by the degradation process, nor the interaction between nodes which share the same environment, which leads to a lower steady value than using EFFN method.

5. Conclusions

For a complex mechatronic system, the effect of a fault node may start from degradation instead of failure.The degradation may spread along traditional edges like cables, roads, radio wave, pipes and so on. Meanwhile, other systems or environment may have an effect on the given system.Those influences of other systems or environment which cannot be described by traditional networks but actually play an important role in the spreading process are modeled as field energy in the proposed novel EFFN.If there is only one sink node and there is no field energy, the network can be regarded as a stochastic flow network. To give a general expression of flow effects and field effects,the proposed EFFN utilizes the concept of energy that different kinds of flow and field effects are uniformly modeled by flow energy and field energy.Compared with the traditional networks, the flow energy is used to replace the flow while the field energy is used to present the effect of the environment and other systems. The field energy can conduct accumulative or shock impact on the connected nodes by assigning different attenuation coefficients, for example, the temperature changes slowly over time and vibration decays heavily.Considering the degradation of the node itself, ADR is used to describe the state transition. The correlations between different nodes with different degradation states are modeled as CDCM. The strength of a field energy on a node is measured by timedependent influencing intensity in this work.

The proposed method is applied to a multi-field coupling degradation propagation process in an aviation actuation system. The propagation path is shown in a timedependent state transition figure which provides the order of degradation intuitively. By combining the output field energy and the input field energy, the degradation modes are analyzed. For a measurable energy system, the application provides a method to estimate the possible failure reason by system energy atlas. The analyzed result is consistent with the given scenario. Compared with the traditional methods, the proposed method takes advantages in analyzing the joint effect of load dynamics and components dependency by providing dynamic failure process, and meanwhile,establishes a unified description of the interdependency between flow energy and field energy.

Acknowledgments

This study was co-supported by the National Natural Science Foundation of China (Nos. 51875014, 51575019,51620105010), Natural Science Foundation of Beijing Municipality (No. L171003) and Program 111 of China.