基于LS-DYNA的综合管廊燃气泄漏爆炸分析

芦建兵

(武汉理工大学 交通学院，湖北 武汉 430063)

0 引 言

城市地下综合管廊是在城市地下建造一个隧道空间并将各种市政管线集于一体,将其统一规划、设计、建设和管理,是解决市政设施建设过程中反复开挖路面造成交通拥堵和资源浪费的有效途径,建成之后也是保障城市生态系统高效有序运行的重要基础设施[1]。随着城市化进程的不断推荐,综合管廊在全国各地都得到了大力发展,其自身的安全性直接关系到城市生命线系统的供给能力,因此对于综合管廊的安全性就有较高的要求。目前,在管廊受燃气爆炸荷载作用下的动力响应和破坏分析方面的研究不是太多,相应的理论研究和技术规范都不是十分完备。在此背景下，本文使用前处理软件Hypermesh建立典型三舱式管廊的有限元模型,再通过LS-DYNA强大的动力分析能力,对湖北省十堰市某三舱式综合管廊进行了燃气爆炸荷载作用下的动力分析,观察爆炸后的破坏状况,为以后综合管廊的抗爆分析和抗爆设计提供参考。

1 有限元模型及材料参数

1.1 有限元模型

选取典型的三舱式管廊结构,其基本尺寸如图1所示,沿管廊的长度方向取10 m进行建模,利用Hypermesh建立几何模型并划分网格。对于燃气舱中的天然气,由于在LS-DYNA软件材料库中并没有具体的材料模型,用其他气体材料替代总会存在不可消除的误差,因此本文将通过TNT当量替换法,通过燃烧热值相同的理论将燃气舱中泄漏的天然气转化为确定当量的TNT炸药来进行建模计算[2]。为了简化计算过程,文中将采用1/2对称建模,在炸药所在截面处建立对称模型。模型主要包括炸药、空气、管廊结构三部分。其中混凝土采用三维实体单元,运用Lagrange网格进行模拟,炸药和空气则运用可以承受大变形的ALE网格,避免出现网格畸变[3]。模拟爆炸荷载与结构的相互作用采用流固耦合算法来实现。模型采用kg-m-s单位制。

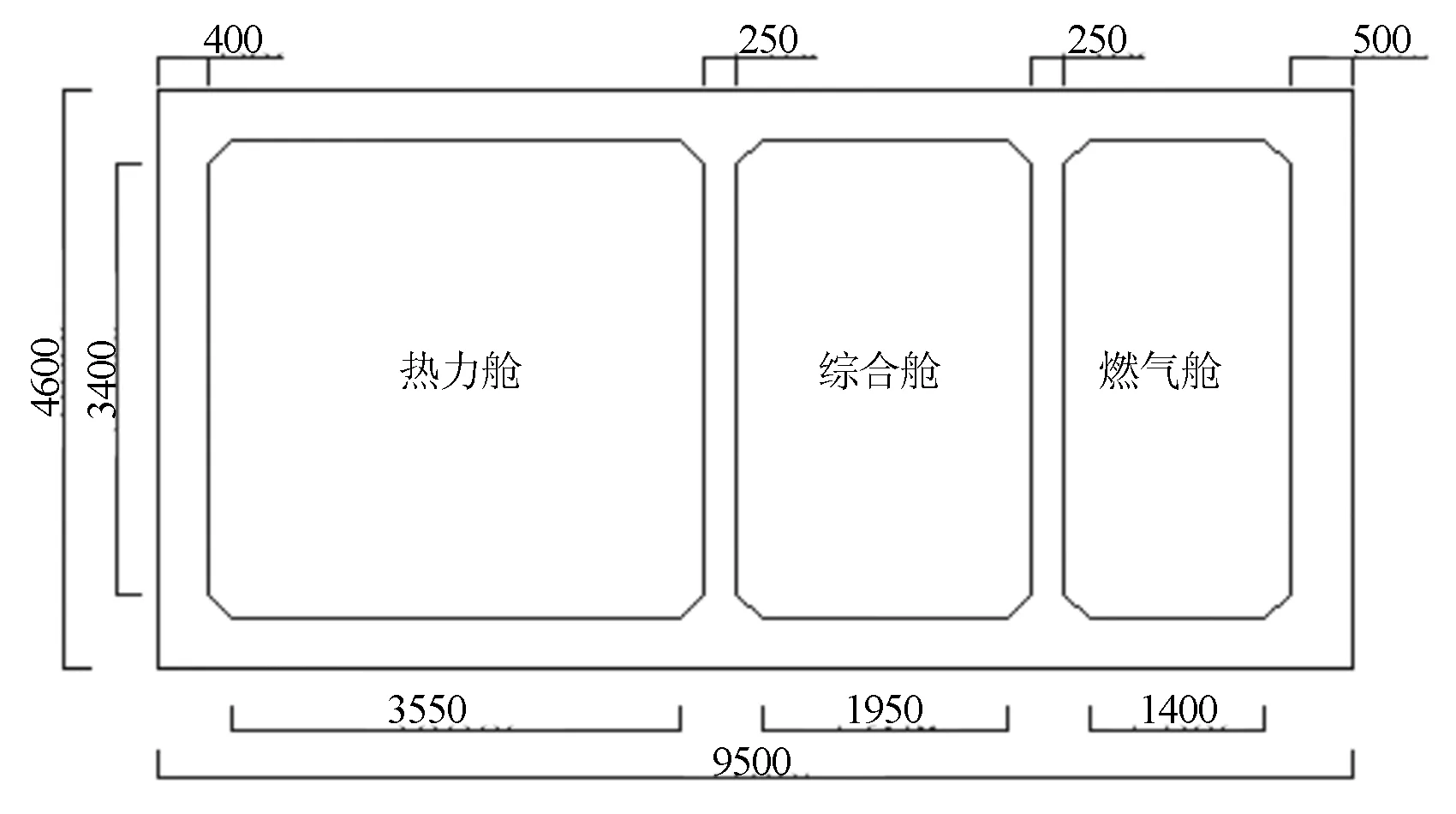
图1 综合管廊结构尺寸(单位：mm)

1.2 材料模型和状态方程

炸药材料采用关键字*MAT-HIGH-EXPLOSIVE-BURN定义,炸药密度Rho=1 630 kg/m3,爆速D=6 930 m/s,爆压Pcj=27 GPa。描述炸药用 JWL状态方程,采用关键字*EOS-JWL定义,其物理含义可表示为:

式中:P为爆轰压力;V为相对体积;E0为单位体积内的炸药内能;A、B、R1、R2、ω均为试验所确定的常数。该状态方程描述了爆炸产物的压力体积之间的关系[4],其具体取值见表1。

表1 炸药状态方程参数表

空气采用的是流体材料模型,采用关键字*MAT-NULL定义,空气状态方程采用关键字*EOS-LINEEAR-POLYNOMIAL定义[5],其物理含义为:

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

空气材料参数和状态方程参数见表2。

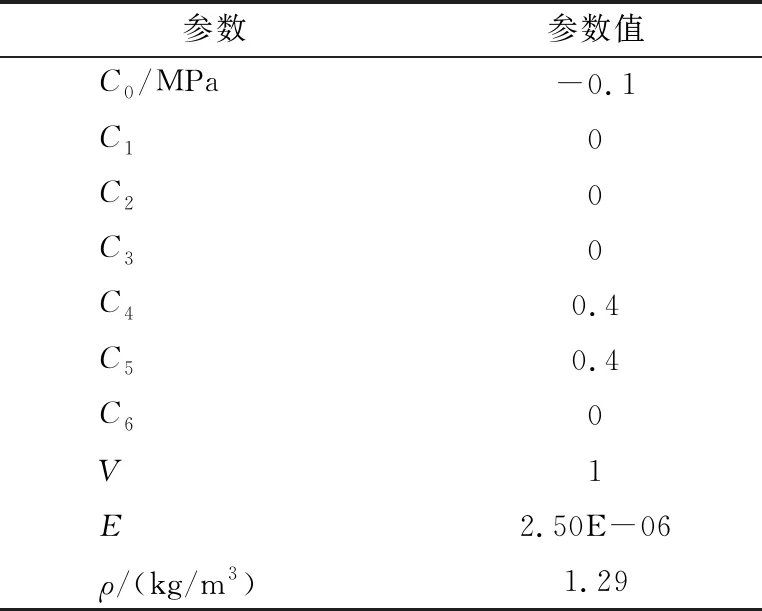
表2 空气状态方程参数表

混凝土材料采用LS-DYNA提供的*MAT-JOHNSON-HOLMQUIST-CONCRET模型,简称J-H-C动态损伤模型,这种模型是均质模型,认为混凝土应变率的改变不会影响其临界应变和极限应变[6]。混凝土材料的本构关系表述如下:

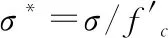
式中:Δεp是等效塑性应变增加量,Δμp是塑性体积应变增加量;D1、D2都是材料常数。其具体材料参数见表3。

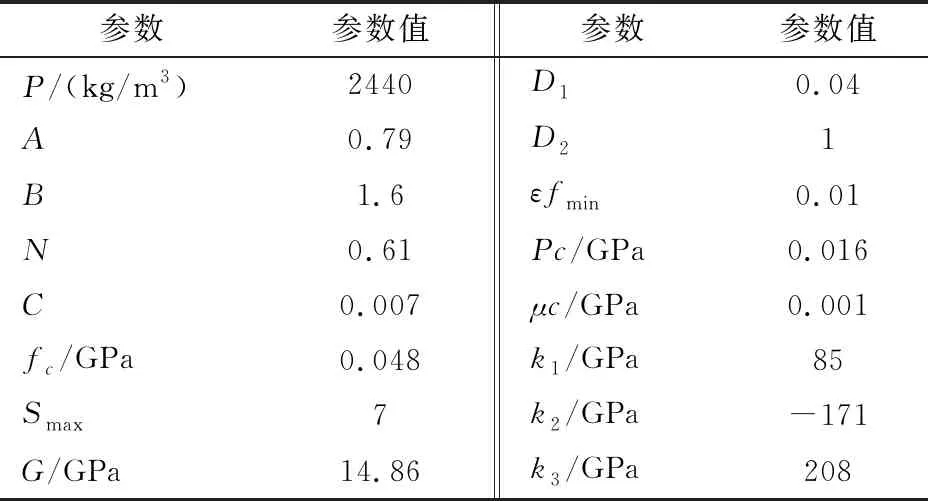
表3 混凝土材料的模型参数

此外,为了表征混凝土在爆炸荷载下的失效情况,对混凝土材料添加失效判据*MAT-ADD-EROSION,当最大主应变达到0.01时,判定混凝土材料失效,删除网格退出计算[7]。

1.3 边界条件

对炸药所在中心截面上的所有节点施加对称Z的法相约束,对沿管廊长度方向10 m处另外一端截面上的空气边缘节点以及结构截面上的节点都施加无反射边界条件[8]。对于管廊四周的土压力,根据土力学的基本知识进行适当简化。管廊的下部节点在爆炸发生时,其各个方向的自由度均受到限制,相当于施加固定约束。管廊顶部有4 m深的土,由于土的自重,管廊顶部会受到压力。对于均质土层而言,其在深度z处平面上的自重应力可表示为

式中:Wz为单位面积上土柱体的自重;A为土柱体的截面积,m2;γ为土的重度,单位kN/m3;z为计算深度。本文中综合管廊埋深为4 m,此处取z=4 m,土的重度为18 kN/m3,因此管廊的顶部压力为72 kN/m2。

管廊侧面可利用静止土压力的理论进行简化,计算其应力[9]。根据静止土压力的概念,在填土表面以下任意深度z处取一微小单元体,在该单元体的水平面上作用着土体的自重应力,该点处的侧向应力可按照半无限体在无侧移条件下侧向应力的计算方法进行计算,这一侧向应力即为静止土压力:

P0=K0γz

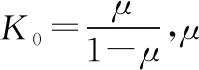
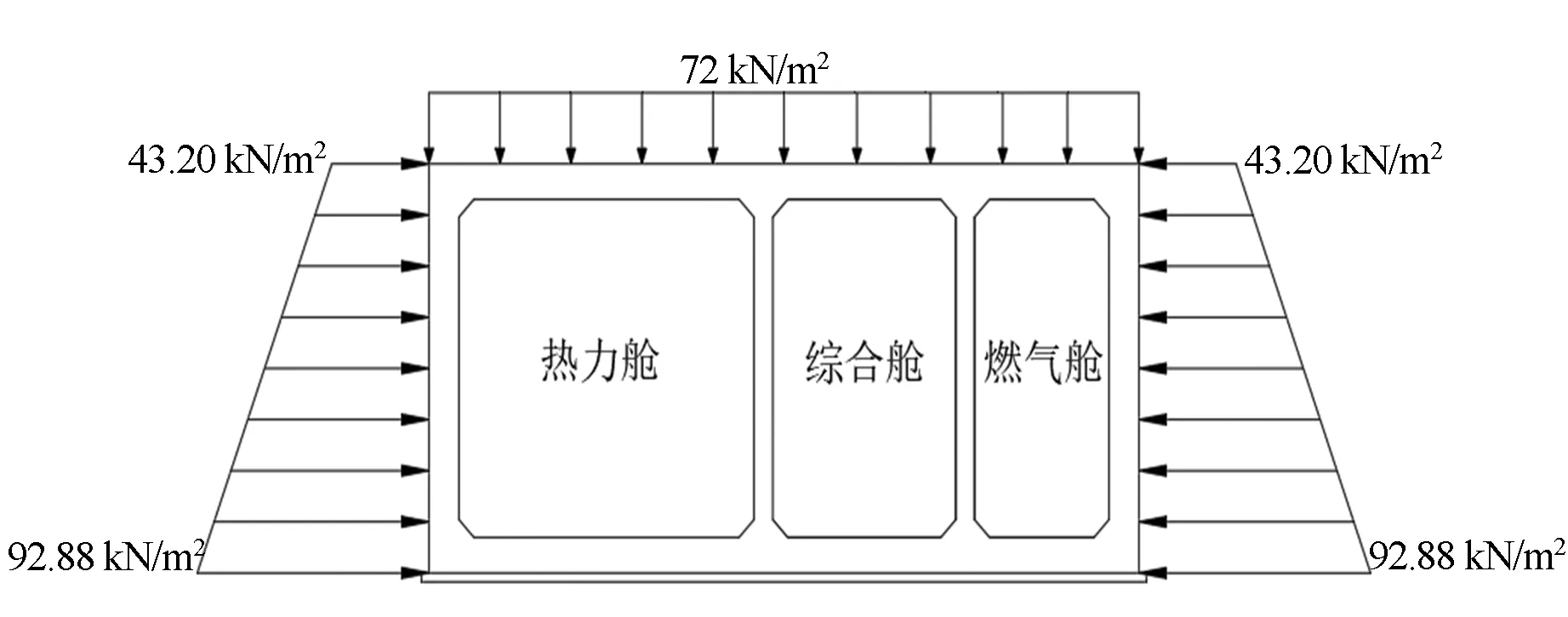
图2 管廊边界受力图

1.4 燃气与TNT的转化

本文中涉及的管廊内的输气管道压力值为0.8 MPa,属于次高压燃气管道A级。输气管道采用其外管径426 mm,壁厚10 mm。根据理想气体状态方程:

式中:P为气体压强,MPa;V为气体体积,m3;n为理想气体的物质的量;T表示理想气体的热力学温度,K;R为理想气体常数,取8.314 mol/(kg·k);m为气体的质量,kg;M为气体的摩尔质量, kg/mol。

由此可得输气管道中天然气的密度为:

考虑常温T=293.15 K情况下,将所有参数代入上式中得到综合管廊中天然气的密度ρ=5.25kg/m3。故10 m长管廊中燃气舱内的天然气总质量m为 7.14 kg。在实际情况下,天然气的泄露爆炸不是所有质量都参与的,用一标量收率n来表征参与爆炸的天然气量,n一般取值为0.1。根据能量守恒定律将天然气总量换算成TNT量来模拟计算[10]:

式中:mTNT为等效TNT的质量,kg;Qd为可燃气云爆炸时释放的总能量,kJ;QTNT为TNT的爆炸热值,取4 500 kJ/kg;Qe为天然气的爆炸热值,取甲烷的燃烧热值5.56×104kJ/kg;m为天然气总质量。

将以上参数代入可得10 m管廊中得天然气爆炸可等效TNT的总量为mTNT=8.82 kg。

建立有限元模型如图3所示。

图3 燃气舱中天然气爆炸有限元模型

2 计算结果分析

2.1 燃气舱中冲击波的传播

为了观测爆炸冲击波在燃气舱中的传播规律,在炸药中心所在的截面处,沿着管廊的长度方向间隔2 m分别布置4个测点A、B、C、D,他们与炸药中心处的距离分别是2 m、4 m、6 m和8 m。

炸药爆炸之后,在燃气舱中开始以冲击波的形式向四周传播,刚开始传播的时候和在自由场中的传播没有很大不同,呈球状传播,之后随着冲击波的继续传播,将会接触到管廊壁,形成一系列的反射,冲击波的传播形式将会与自由空气场中表现出很大的不同,不会形成规则的冲击波进行传播。图4所示为测点A处的超压-时程曲线。

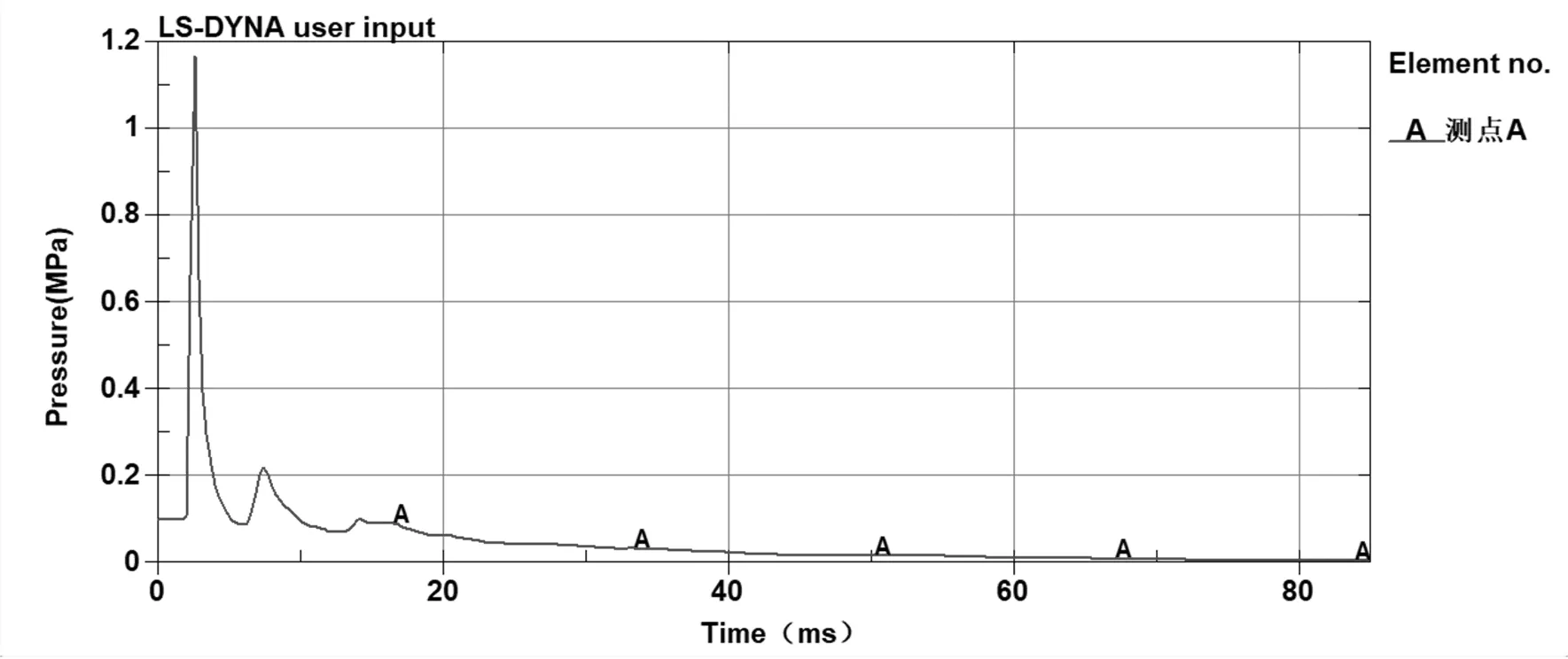
图4 测点A处的超压-时程曲线

由图4可以看出,在t=2.6 ms时,A处的空气超压值迅速达到了1.17 MPa,然后又快速减小,当t=5.4 ms时超压峰值降到最低谷,然后再次变大,经历了这样三次增大减小的过程后平缓地变为0。图4中可以看出超压增大的速度要快于减小回落的速度(增大与减小的斜率不同)。出现这样空气超压值反复变化的原因是在管廊内部冲击波的多次反射。

图5中所示为各个测点处的超压-时程曲线。

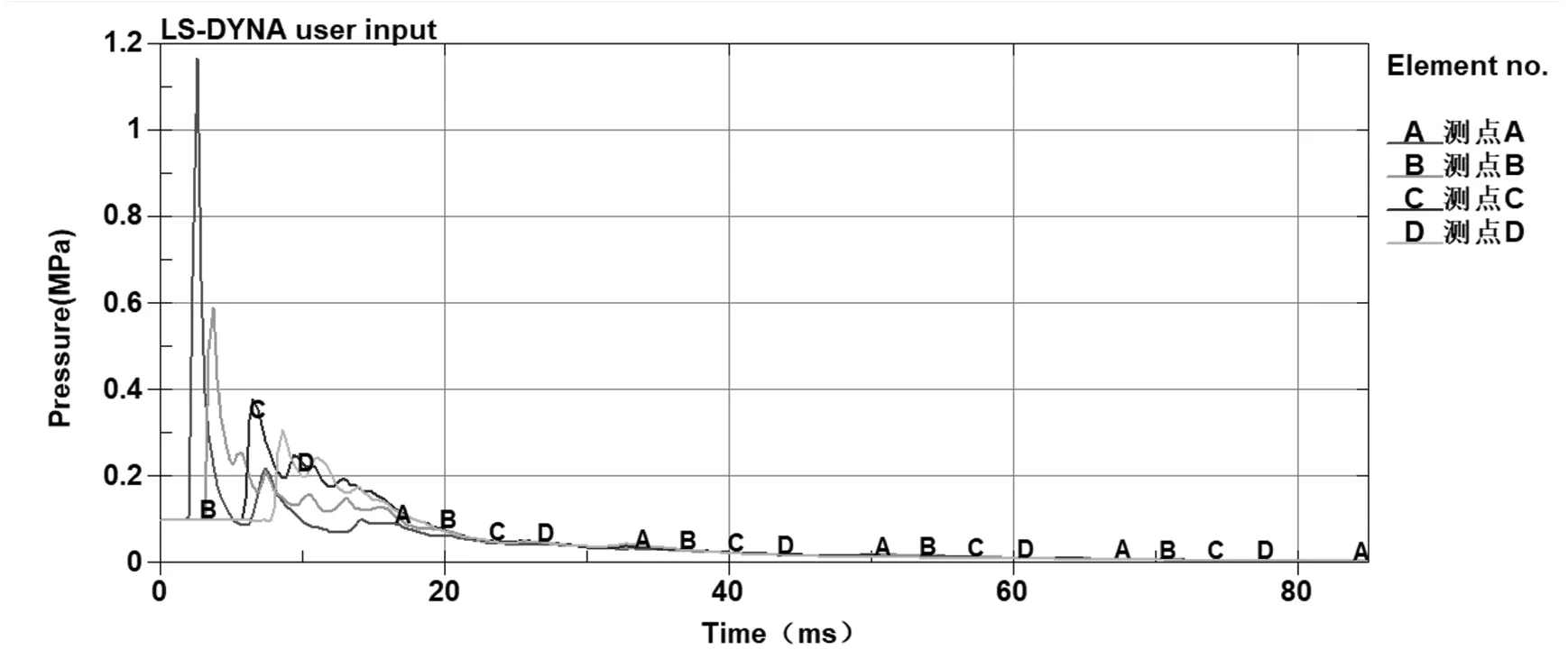
图5 各个测点处的超压-时程曲线

由图5可以看出,随着与炸药中心处的距离增大,B、C、D三点处的超压峰值依次降低,各点处到达峰值的时间随着距离的增大不断变长。当t=3.7 ms左右时,B处的空气超压值达到了0.59 MPa;t=6.6 ms左右时,C处的空气超压值达到了0.38 MPa;t=8.6 ms左右时,D处的空气超压值达到了0.31 MPa;同测点A处的超压峰值的变化类似地,由于B、C、D三点处也出现了超压峰值往复变化的现象,经过多次波动都平缓地变小,这种变化的特点与在自由空气场中的变化截然不同,其超压峰值也较空气中爆炸时的更高。

2.2 燃气爆炸后管廊的动态响应

2.2.1 位移变化

在上述爆炸过程中,选取破坏较为严重的位置,如隔墙的中心处、管廊上部两角位置等比较典型的位置,观察其位移的变化过程。各测点的选取如图6 所示,编号分别为测点1、2、3、4、5、6、7、8。

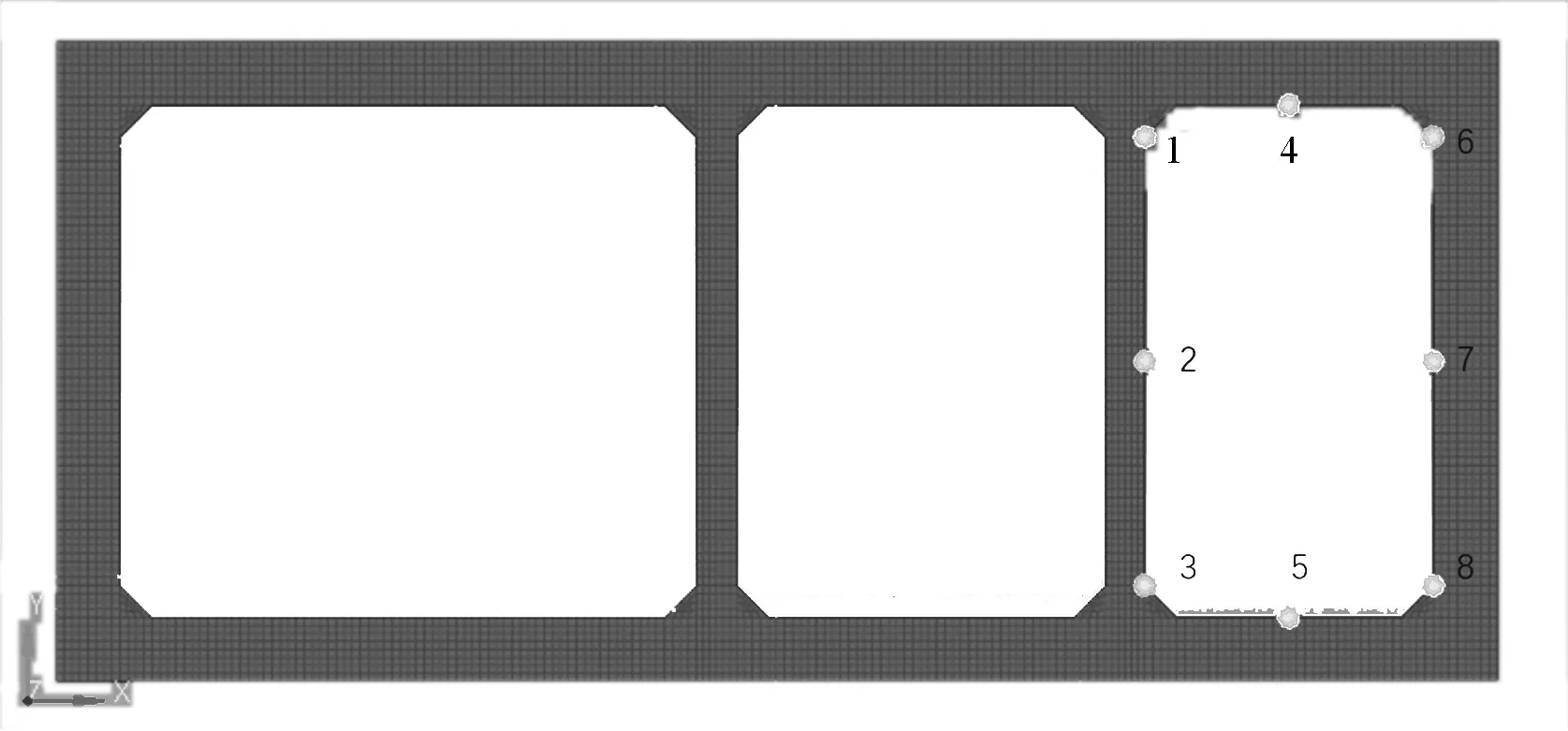
图6 燃气舱中位移观测点

各个位置处测点的位移-时程曲线如图7所示。

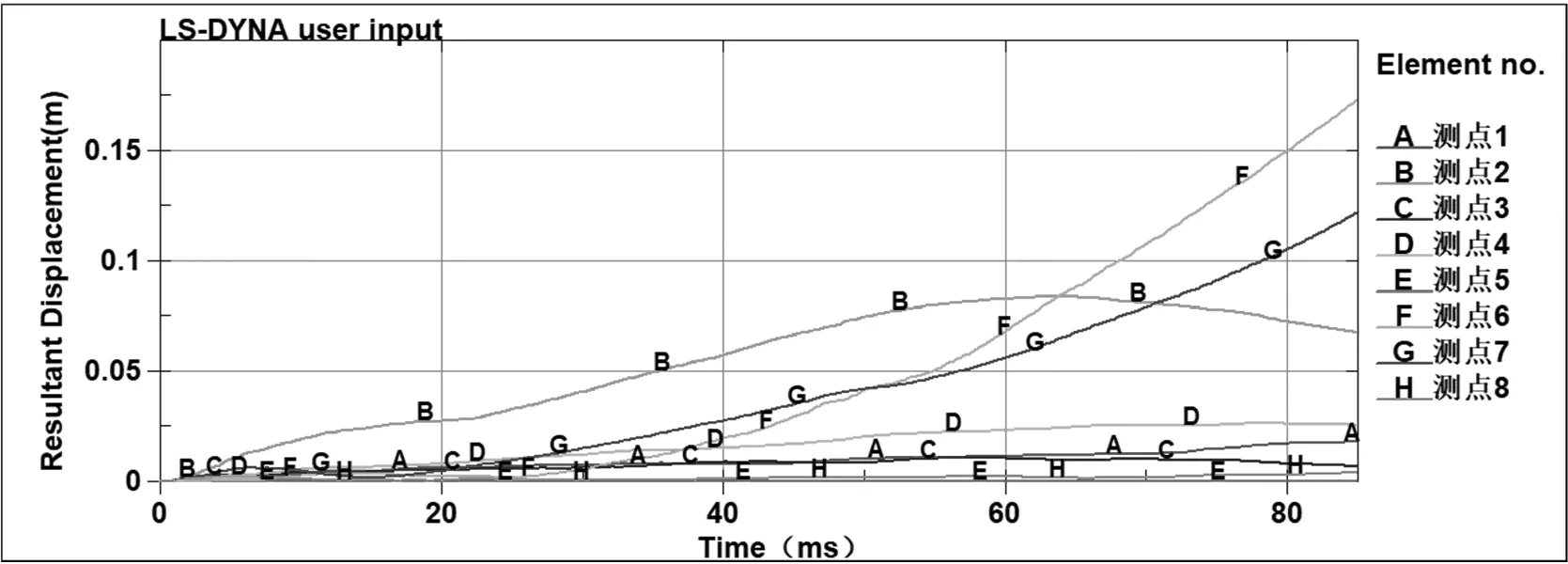
图7 燃气舱中各点位移-时程曲线

由图7可以看出,测点6、7(燃气舱侧墙上部和中部)的位移最为明显,特点是在爆炸刚开始并没有发生位移,到t=20 ms时位移开始变大,随着爆炸过程的进行位移一直增大,没有出现收敛的趋势,燃气舱侧墙出现倾覆。测点2(隔墙中部)的位移不同于其他,该点处的位移从爆炸一开始就开始增大,到t=60 ms时达到最大位移0.084 m,然后位移再次减小。测点4(管廊上顶板)处的位移在爆炸一开始就出现变化,达到一定程度之后将不再发生变化,保持稳定。测点3、5、8(隔墙底部、下底板、侧墙底部)三处测点的位移在整个爆炸过程中都不明显,没有发生大的变化,可以看出燃气舱中爆炸时对于管廊底部的影响最小。

在整个爆炸过程中,测点位移的变化以t=60 ms为界，可以分为前后两个阶段,尤其是测点2(隔墙中部)和测点6、7(侧墙上部和中部)这三点的位移变化尤其明显,测点2在t=60 ms时位移达到了峰值然后开始减小,而测点6、7的位移变化在t=60 ms后速度都有所增大。之所以出现这种现象，可以理解为管廊在爆炸过程中的破坏也分为两个阶段:管廊受到爆炸冲击波的作用发生一定的位移,对管廊结构的整体性造成一定的破坏,这属于第一阶段的破坏,对应图7中60 ms以前的位移变化;整体性破坏之后在土压力的推动作用下,造成管廊结构的第二阶段破坏,在图7中就表现出60 ms之后的变化特点。

2.2.2 速度变化

爆炸发生后由于冲击波在管廊壁的多次反射作用,燃气舱各点的速度变化都比较复杂,为了更清晰地表达速度的变化特点,现分析位移时程图中位移变化最有特点、变化最大的三个测点2、6、7的速度变化情况。图8所示为测点2(燃气舱隔墙中心处)、测点6(燃气舱侧墙顶部)和测点7(燃气舱侧墙中心处)的速度-时程曲线。

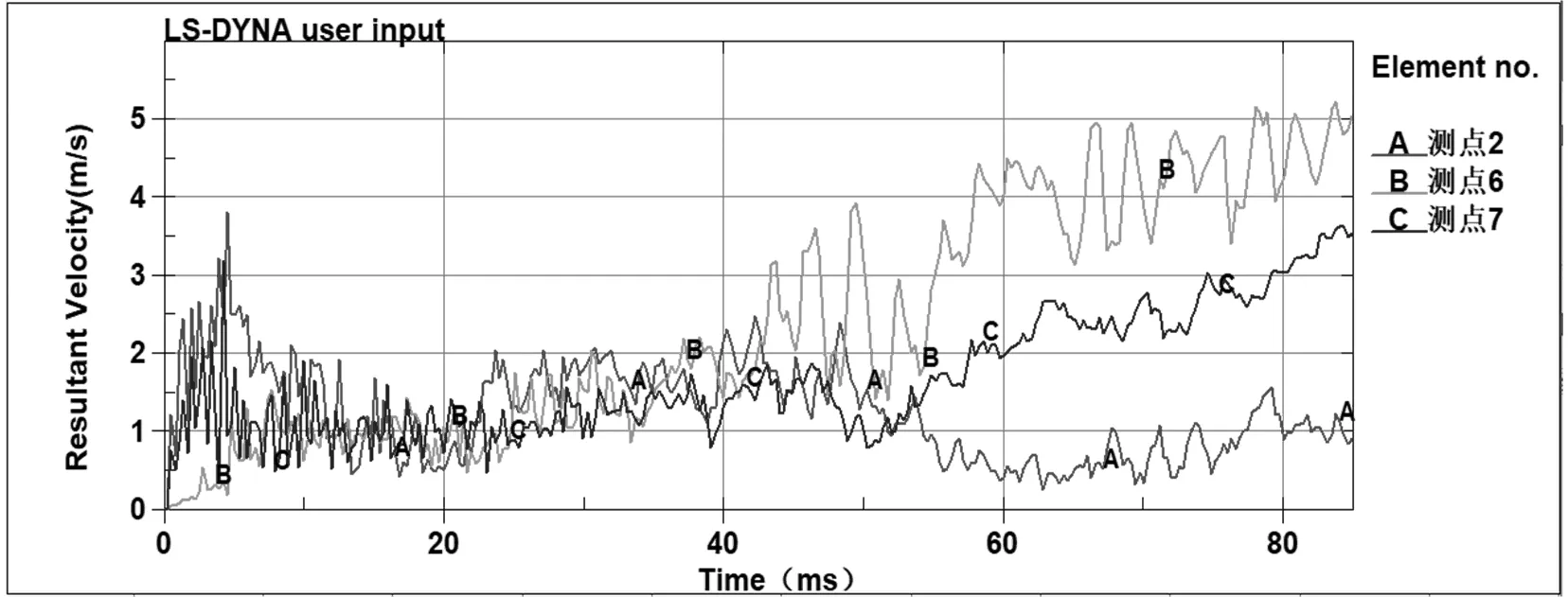
图8 燃气舱中各点的速度-时程变化曲线

由图8可以看出,在爆炸过程中各点的速度都呈现出波动变化的特点,爆炸一开始,各点处受到冲击波的作用,速度都发生了突变,然后呈现波动增大的变化趋势。在t=40 ms之前三点处的速度变化趋势基本保持一致,然后测点6、7的速度呈现出逐步波动增大的趋势,测点2的速度先减小,后增大,但是最后的速度大小均小于测点6、7。这三点的位移变化的不同,也反映出管廊爆炸破坏分为两个阶段,第一阶段爆炸荷载本身产生的破坏反应,2、6、7三点的速度变化较为一致;第二阶段在土压力的作用下,测点6、7所在的侧墙直接和管廊周围土接触,在土的推动下速度不断增大,最后造成管廊侧墙倾覆。

2.3 燃气爆炸对管廊的破坏效应

管廊在经过爆炸冲击波的一系列作用之后,发生的破坏效应可以分为两个阶段:第一阶段是爆炸冲击波对于管廊产生的直接破坏,具体表现为在管廊壁的表面造成混凝土的剥落侵蚀,在受拉部位产生强烈的拉应力,造成管廊出现一系列沿着管廊长度方向的裂缝,影响到管廊的整体性(图9);第二阶段是在管廊整体性受到破坏之后,周围的土压力由于失去了平衡,会从静止土压力变为被动土压力,作用在管廊结构上面,对管廊进行二次破坏,造成管廊的倾覆(图10)。

图9 管廊燃气舱爆炸第一阶段破坏图

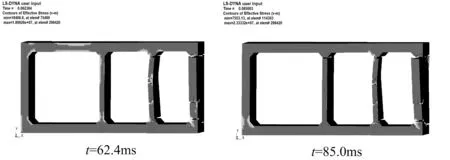
图10 管廊燃气舱爆炸第二阶段破坏图

由图9可以看出,爆炸开始后,管廊燃气舱的上顶面处两个角的位置以及侧墙和隔墙的背部位置均出现了沿着管廊长度方向的裂缝,同时管廊内底部和侧面出现混凝土剥落现象。隔墙的背部出现裂缝是因为燃气舱内爆炸之后形成冲击波作用在侧面隔墙上,表现为压应力,因此隔墙背部形成拉应力,造成混凝土受拉破坏,形成裂缝;管廊上部两角的位置出现明显裂缝,但是在底部两角处裂缝不明显,主要原因是炸药距离下底面较近,因此上部相对于下底面而言是背爆面,受到的破坏作用更大,从而形成沿着管廊长度方向上的明显的裂缝。

由图10可以看出,随着时间的推移,爆炸产生的裂缝沿着管廊进一步延伸,管廊的整体性遭到破坏,管廊侧墙在土压力的作用下有向着管廊内部运动的趋势,在侧墙的外侧底部形成拉应力,在侧墙根部形成拉伸断裂,造成了墙体的倾覆破坏。这就是管廊爆炸破坏后由于土压力作用形成的第二阶段的破坏效果。

3 结束语

本文中运用有限元软件LS-DYNA进行仿真建模的方法,以实际项目中的管廊为研究背景,运用Hypermesh软件建立有限元模型,然后用ANAYA/LS-DYNA进行数值分析,分析了管廊中天然气爆炸后综合管廊中冲击波的传播衰减情况和对管廊的动态响应,观察了管廊破坏的特点。文中将天然气利用能量守恒转化为TNT进行建模计算,通过计算可知,管廊中燃气泄漏爆炸后会对管廊的结构造成破坏性损伤,严重影响其功能性。燃气舱爆炸的破坏过程可以分为两个阶段:第一阶段是由于爆炸冲击波产生的破坏作用,其在燃气舱墙角位置以及隔墙的背侧中心处形成沿着管廊长度方向的裂缝,破坏管廊整体性;第二阶段是在管廊上部以及侧面土压力的作用下,管廊在完整性被破坏以后又遭到再次破坏,从而造成管廊倾覆坍塌。遗憾的是没有实际的管廊爆炸试验信息与此进行对比分析,因此管廊爆炸方面的研究有待进一步深入。