斜腹板箱梁有效宽度计算方法的研究
单巍巍
(安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088)
0 引 言
《公路钢筋混凝土及预应力混凝土桥涵设计规范》(下文简称桥梁规范)采用《德国规范DIN1075》中推荐的方法计算箱形截面梁翼缘有效宽度,并根据大量实桥验算和空间有限元方法计算对某些参数进行了修正。该方法计算简单,在设计中得到广泛应用。但是桥梁规范对斜腹板箱梁不折减宽度b值未给出明确规定,使设计人员在桥梁计算中采用不同的计算方法,造成计算结果的不统一。本文以某匝道桥为计算模型,采用不同方法计算箱梁有效宽度,并对箱梁顶、底缘应力进行分析,为斜腹板箱梁桥的工程设计提供参考。
1 箱梁有效宽度的原理
T梁、箱梁等带肋梁结构在外力作用下产生弯曲内力和变形,通过梁肋的剪切变形传递给翼板。剪应变在向翼板内横向传递的过程中是不均匀的,在梁肋与翼缘板的交接处最大,随着与梁肋距离的增加而逐渐减小,使翼板远离肋板处的纵向位移滞后于肋板边缘处,使弯曲应力的横向分布呈曲线形状(图1)。
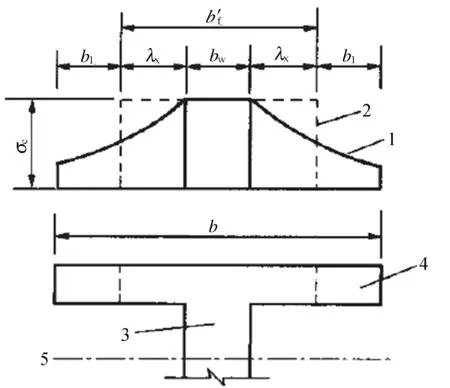
图1 带肋梁应力示意图
由翼板的剪切变形而造成的弯曲正应力沿着梁宽度方向不均匀分布,这种现象称为“剪力滞(后)效应”。而这个应力峰值通常大于我们按初等梁理论计算出来的值。工程设计人员提出了“有效宽度”的概念,即将翼缘实际宽度按某个系数或者某种规律折减为计算宽度,使折减后的宽度按初等梁理论算得的应力值和实际的峰值接近,以确保结构的安全。
2 桥梁规范的规定
桥梁规范中第4.2.3条规定,箱形截面梁在腹板两侧上、下翼缘的有效宽度bmi可按下列规定计算(图2):
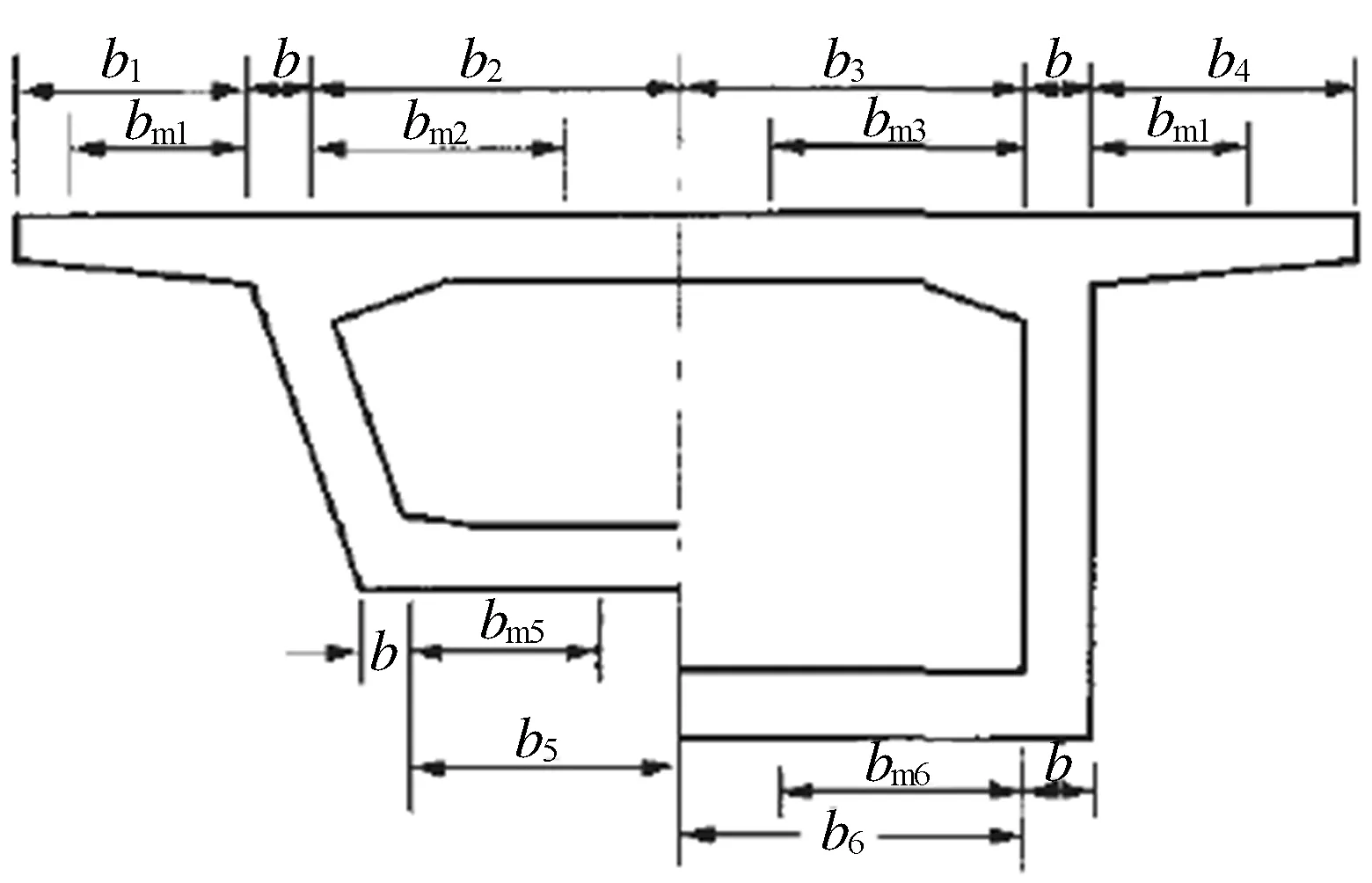
图2 箱型截面梁有效宽度
简支梁和连续梁各跨中部梁段,悬臂梁中间跨的中部梁段:
bmi=ρrbi
(1)
简支梁支点,连续梁边支点及中间支点,悬臂梁悬臂段:
bmi=ρsb
(2)
设计计算中,箱梁的有效宽度为2×(b+bmi),b为箱梁不折减宽度。
3 斜腹板箱梁有效宽度的计算方法
由图2及有效宽度原理可知,直腹板箱梁的不折减宽度b取腹板的宽度,而斜腹板箱梁不折减宽度b的取值,规范中并没有做明确的规定。实际设计中,对于斜腹板箱梁不折减宽度b的取值,有以下三种方法(图3):
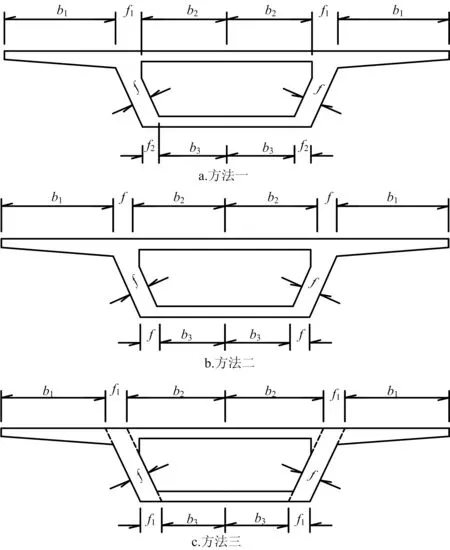
图3 斜腹板箱梁不折减宽度取值方法
由图3可知,方法一中不折减宽度取腹板处外轮廓折点与内轮廓折点的水平距离;方法二中不折减宽度取斜腹板的垂直宽度;方法三中不折减宽度取斜腹板的水平宽度。
4 依托工程
通过依托的桥梁工程,用三种方法计算箱梁顶、底缘的有效宽度,并对恒载、标准组合和短期组合下顶、底缘应力进行对比分析。该桥为某匝道桥,桥跨为3×30 m,上部结构为现浇连续箱梁。箱梁顶缘宽9 m,底缘宽3.4 m,梁高1.8 m,斜腹板斜率为1.333,其截面构造如图4所示。
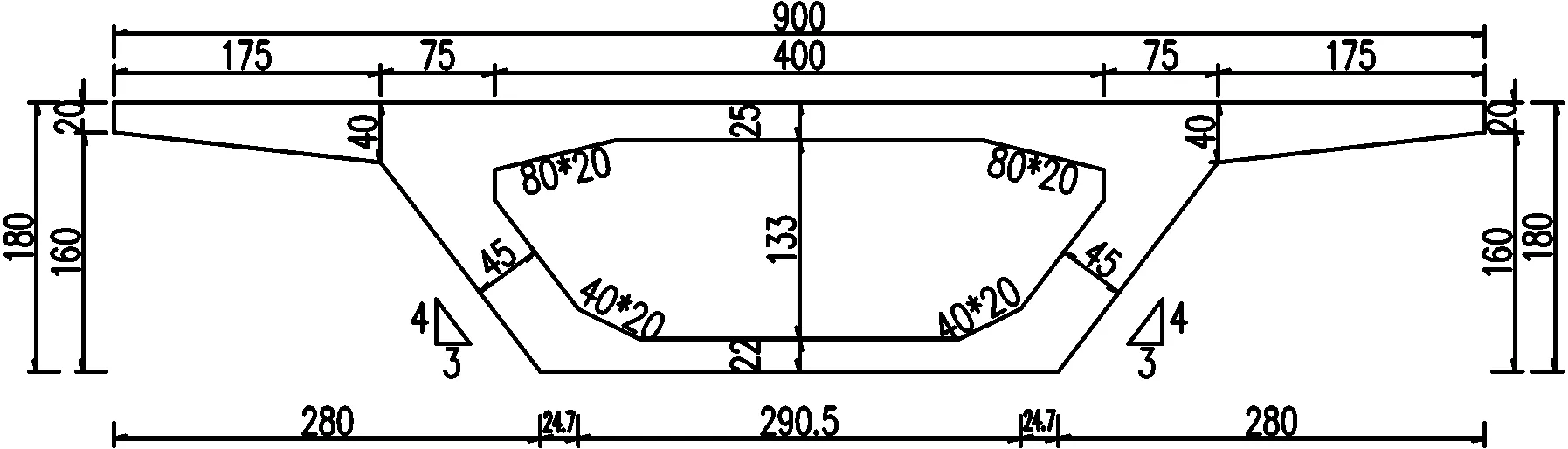
图4 箱梁标准截面构造图
5 计算结果对比与分析
5.1 建立计算模型
采用桥梁博士程序建立桥梁上部有限元模型。在模型中选取7个关键位置(图5)进行对比分析,7个位置分别为:1为第一跨端支点;2为第一跨跨中;3为第一、二跨中支点;4为第二跨跨中;5为第二、三跨中支点;6为第三跨跨中;7为第三跨端支点。

图5 箱梁桥有限元模型
5.2 计算有效宽度
分别按斜腹板箱梁不折减宽度的三种取值方法得到腹板两侧各翼缘的实际宽度,采用桥梁规范4.2.3条计算各翼缘的有效宽度,最后得到三种方法下箱梁顶、底缘的有效宽度值,见表1。

表1 箱梁顶、底缘有效宽度
由表1可知,边跨跨中的顶、底缘有效宽度最大,中支点处的顶、底缘有效宽度最小;方法一计算的顶缘有效宽度最大,方法二最小,并且在中支点处相差最大,差值达10.8%;方法三计算的底缘有效宽度最大,方法一最小,并且在中支点处相差最大,差值达12.8%。
5.3 应力对比分析
按三种有效宽度计算恒载、标准组合和短期组合下箱梁顶、底缘应力,结果见表2~表4。表中最大、最小应力为全桥应力的最大、最小值。

表2 恒载作用下顶、底缘应力

表3 标准组合下顶、底缘应力
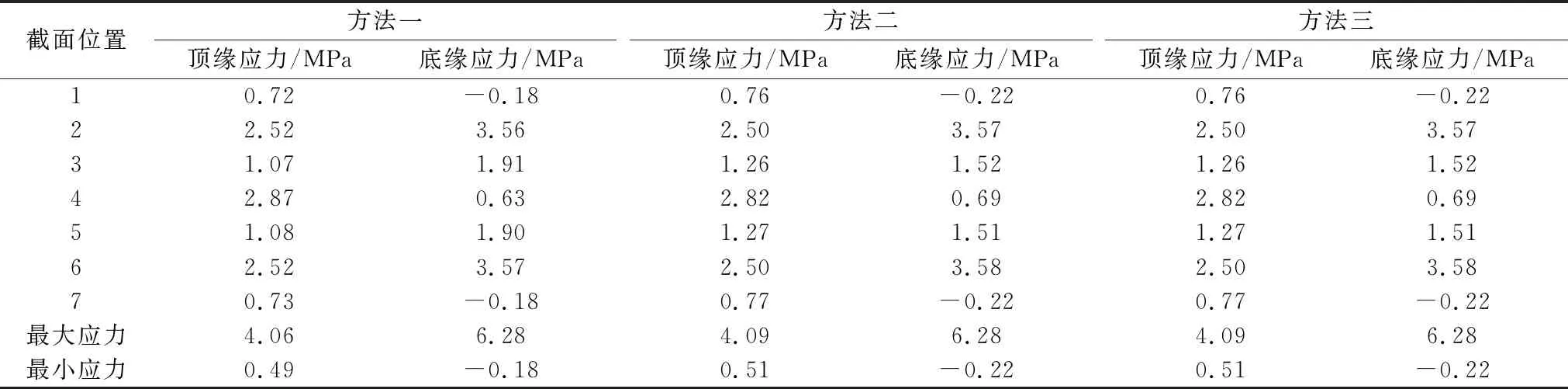
表4 短期组合下顶、底缘应力
由表2~表4可知:
(1)斜腹板箱梁有效宽度的不同计算方法对跨中截面(2、4、6号点位置)顶、底缘应力影响较小,可以忽略不计,而对支点截面(1、3、5、7号点位置)顶、底缘应力影响较大。边支点应力较小,对结构设计不起控制作用,因此有效宽度的不同计算方法主要影响中支点截面的应力。
(2)采用方法三计算的恒载作用下中支点截面顶缘应力最大,方法一最小,相差0.34MPa;采用方法一计算的恒载作用下中支点截面底缘应力最大,方法二与方法三最小,相差0.45 MPa。
(3)采用方法二计算的标准组合下中支点截面顶缘最大应力最大,方法一最小,相差0.51MPa;采用方法一计算的标准组合下中支点截面底缘最大应力最大,方法三最小,相差0.88MPa。
(4)采用方法三计算的短期组合下中支点截面顶缘最小应力最大,方法一最小,相差0.34MPa;采用方法一计算的短期组合下中支点截面底缘最小应力最大,方法二最小,相差0.39MPa。
(5)恒载、标准组合及短期组合作用下全桥最大应力与最小应力值,三种方法的计算差值均小于0.1MPa。
6 结 论
(1)对于该匝道桥,方法一计算的顶缘有效宽度最大,方法二最小,并且在中支点处相差最大,差了10.8%;方法三计算的底缘有效宽度最大,方法一最小,并且在中支点处相差最大,差了12.8%。
(2)斜腹板箱梁有效宽度的不同计算方法,对跨中截面积最大、最小应力值影响较小,设计中可忽略不计。
(3)斜腹板箱梁有效宽度的不同计算方法,对中支点截面应力影响较大,应力最大相差0.88MPa,进行桥梁设计时应注意有效宽度计算方法的选用。

