岩石抗压强度的统计推断——应用自助法的实例

蓝兆松

(福州市规划勘测设计研究总院 福建福州 350108)

1 工程概况

福州市规划勘测设计总院(下文简称“我院”)承担了某区间详勘成果钻孔抽样验证工作，具体包含外业钻探及室内岩石抗压试验两大项工作。3个抽样验证钻孔均由业主指定，分别为Q3XZ1、Q3XZ3及Q3XZ16孔。为本次核查小组验证工作提供3个验证孔岩石抗压试验资料。

外业钻探及取样依据现行标准《建筑工程地质勘探与取样技术规程》进行；岩石制样及抗压试验依据现行国标《工程岩土试验方法标准》进行。

依据原孔的取样深度进行取样，并在其它深度(主要为穿越隧道段)加取若干岩样。利用钻探岩芯样制作成可满足抗压试验要求的岩石试件，所有岩石试件均进行天然状态下单轴抗压强度试验。

1.1 工作实施

1.1.1放样定点

根据原勘3个孔的坐标，采用卫星定位仪GPS-RTK在现场找到原勘3个孔(Q3XZ1、Q3XZ3及Q3XZ16)并得到原勘单位确认后，在3个孔边上各布置1个钻孔，钻孔编号分别为YZ-Q3XZ1、YZ-Q3XZ3及YZ-Q3XZ16。与原孔孔距分别为0.5m、0.8m及0.92m，均控制在1m以内，高程基本一致，满足核查要求。3个钻孔孔深均控制在穿过隧道底板下1m～3m。

1.1.2钻探及封孔

采用XY-100型钻机，金刚石钻头，泥浆护壁回转钻进工艺，钻探过程严格控制回次进尺，所取岩土芯均进行现场摆样，确保了岩土层分层的准确性。

1.1.3取样及制样

原则上取样位置(标高)与原孔一致，位置一致处若岩芯破碎，则在上下相邻处取相对较为完整的岩芯样。对确认的岩芯样进行孔号及深度标记并密封保存。此外，在其它深度(穿越隧道段)加取若干岩芯样。3个钻孔施钻完毕，集齐所有同深度岩样后通知业主联系核查小组现场见证制样过程。

1.1.4抗压试验

同深度岩样制样完毕后，在我院土工试验室进行天然单轴抗压强度试验。先进行各岩样复核，再进行各岩样尺寸测量，最后进行抗压试验并将结果换算成标准试样抗压强度指标。

1.2 抗压试验成果

本次抗压试验分2次进行，第1次进行与原勘钻孔同深度岩样的天然单轴抗压强度试验，具体试验结果见表1，为a组数据。第2次进行余下岩样的天然单轴抗压强度试验，具体试验结果见表2，为b组数据。

表1 同深度岩样天然单轴抗压强度成果表(a组数据)

表2 余下岩样天然单轴抗压强度成果表(b组数据)

从钻孔放样、外业钻探、选取岩样、制作样本以及抗压试验等全过程均在核查小组各方成员共同见证，确认获得的岩石抗压试验数据真实可靠。

2 规范给出的统计方法

2.1 统计指标

根据《岩土工程勘察规范》(GB500021-2001,2009年版)，对指标进行统计。按有关规范及试验、测试要求的方法，对室内试验和原位测试的数据进行统计获取指标。其中的标准值，按不利组合考虑。岩土层指标数据的粗差，剔除原则上采用三倍标准差法，个别数据由于岩土层的不均匀性或为夹层而造成数据离散性明显较大的，也予以剔除。有关参数的平均值φm、标准差σf、变异系数δ、标准值φk的计算公式如下[1]：

(1)

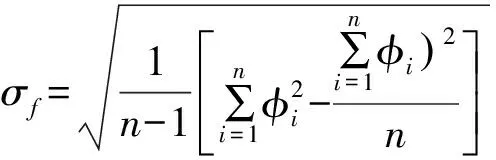
(2)

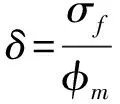
(3)

岩土参数标准值：φk=γsφm

(4)

(5)

式中：

φm——岩土参数的平均值；

n——参加统计的子样数；

σf——岩土参数的标准差；

δ——岩土参数的变异系数；

γs——统计修正系数，式中正负号按不利组合考虑。

2.2 统计数据的可靠性

统计数据源于试验资料，试验样品源于采样。本次工作中所有岩样，样品具有代表性，试验测试方法与操作正确，数据合理。

2.3 指标的统计值与建议值

表1(a组数据)的统计结果：平均值=92.0417;标准差=41.4695;总数=12;变异系数=0.4506;标准值=113.7878;最大值152.4;最小值32.3。

表2(b组数据)的统计结果：平均值=71.4219；标准差=26.0831；总数=32；变异系数=0.3652；标准值=79.3980；最大值136.2；最小值38.3。

《岩土工程勘察规范》(GB50021-2001)采用随机场理论，能较好模拟岩土的空间变异性和相关性，但是涉及到岩土相关距离的合理取值问题的影响，该方法未实际运用[2]。而且，此处a组数据属于小样本，样本数量对参数统计推断值有影响。在相同的置信度及变异系数情况下,试验数量越小,参数统计均值及可靠指标的相对误差就越大，即可靠指标与试验数量、参数统计置信度及参数的变异系数有关[3]。据此处结果可知，变异系数较大。想得到的不是几个岩样数据，而是总体的趋势。下一步，利用自助法进一步进行探讨分析。

3 利用自助算法

总体的分布F未知，但是已经有一个容量为n的来自分布F的数据样本，自这样本按放回抽样的方法抽取一个容量为n的样本，这样的样本称之为自助样本。相继地，独立自原始样本中选取很多个bootstrap样本，利用这些样本对总体F进行推断统计的方法，称为非参数bootstrap方法[4]，即自助法。

Bootstrap算法是现代统计学上的一种重要的方法。即利用有限的样本经多次有放回的重复抽样，重新建立起足以代表母体样本分布之新样本。bootstrap可以指依赖于重置随机抽样的一切试验，可用于计算样本估计的准确性。对于一个采样，只能计算出某个统计量(如均值)的一个取值，无法知道均值统计量的分布情况，通过自助法则可模拟出均值统计量的近似分布。通常新样本的数量可取为1000～10000。精度要求高的话，可以增加新样本的数量。用非参数估计的优点是，不需要对总体分布作任何的假设，且在小样本时也适用。无需假设所研究的总体的分布函数F的形式，样本来自于已知的原始样本数据，方法简单。

自助算法需要大量的计算，要依靠强大计算功能的计算机才能方便进行。本文中的数据分析和计算通过MATLAB语言来完成。MATLAB具有强大的科学计算和分析功能，具有简单易学的编程语言和包罗万象的工具箱，可以使用其内部函数进行计算，还可以根据自己的算法进行扩展编程。

下文简介该工程中利用自助法得到的岩石抗压强度自助样本的平均值、置信区间及假设检验实现统计推断的方法，来进行对数据的分析和讨论。

3.1 平均值

将B个自助样本的均数进行平均就得到自助样本均数，用此代表总体均数。令s(x*i)为第i个自助样本的均数，i=1,2，…，B,则自助样本均数：

MATLAB程序文件如下：

% 岩石强度bootstrap法计算：

y=[43.0,35.4,62.9,97.5,115.9,106.0,103.8,139.2,152.4,80.0,136.1,32.3]

ma=bootstrp(10,@mean,y);

mb=bootstrp(100,@mean,y);

mc=bootstrp(1000,@mean,y);

md=bootstrp(10000,@mean,y); % 得到bootstrap法抽样的均值

Tma=ma′;

Tmb=mb′;

Tmc=mc′;

Tmd=md′;

M0=mean(y)

S0=std(y)

M1=mean(Tma)

S1=std(Tma)

M2=mean(Tmb)

S2=std(Tmb)

M3=mean(Tmc)

S3=std(Tmc)

M4=mean(Tmd)

S4=std(Tmd)

xm=[1 10 100 1000 10000]

ym=[M0 M1 M2 M3 M4]

ys=[S0 S1 S2 S3 S4]

semilogx(xm,ym,′o-′,xm,ys,′x-′)

legend(′均值′,′标准差′)

xlabel(′抽样次数′)

ylabel(′参数估计值′)

grid on

运行以上程序得到图1。图1为自助法抽样次数与参数估计值关系图。横坐标为抽样次数，横坐标采用对数坐标；纵坐标为参数估计值(岩石单轴抗压强度)。蓝线所示为均值，红线所示为标准差。从实践来看，计算抽样次数在1000次以上时计算结果趋于稳定。如图中抽样1000次计算时，均值为92.2273MPa，标准差为10.9148MPa。依靠MATLAB强大的函数功能，在实际计算中，计算时间成本很小。

图1 自助法抽样次数与参数估计值关系图

图2为自助法抽样10 000次的抗压强度平均值的频率直方图和正态分布密度曲线。从图来看，近似正态分布。

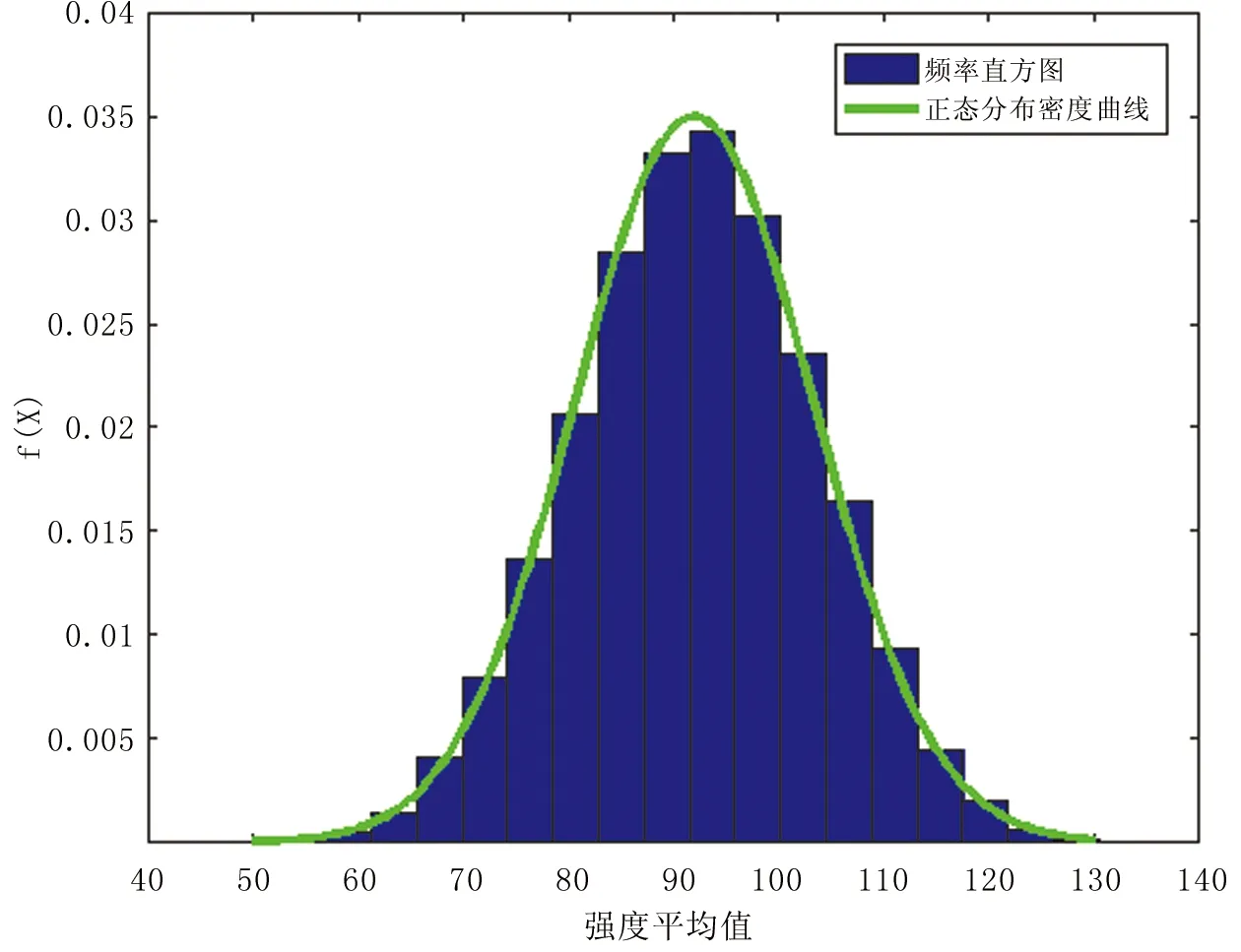
图2 抗压强度平均值的频率直方图和正态分布密度曲线

3.2 置信区间

利用分位数法计算置信区间[4-5]。利用有放回的抽样产生B个自助样本(1个自助样本的样本容量为N，本文中a组数据的N=12)，计算每个自助样本均数s(x*i),i=1,2,…,B，可得到均数的抽样分布，将自助样本均数按从小到大排列，从数据两端各截去∝B/2个观察值(1-α为置信水平，在岩土工程中一般取为95%)，便得到分位数法置信区间，即表示为：

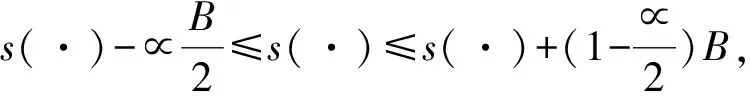
3.3 假设检验

假设两组数据没有显著差异，H0：μ1-μ2=0

(2)重复以上步骤1999次，共获得2000个W值，按照从小到大排列，得到W2.5%和W97.5%，若区间(W2.5%，W97.5%)包含0，则接受原假设，否则拒绝原假设。

随后，计算判断a组数据与b组数据是否存在显著性差异。利用此方法计算，编写MATLAB语句文件计算，抽样2000次计算得本例子(W2.5%，W97.5%)区间为 [-4.1344，43.7958] ，包含0，接受原假设，易知通过a、b两组数据的显著性差异的比较，结果显示不存在显著差异，表明样本来自于同一总体。采用上述方法可以很方便地比较原勘数据与此次抽样验证数据的差别。该方法及结果可提供设计和施工参考使用。

4 结语

作为自然、历史产物的岩土，其成分、结构和构造充满随机性和不确定性，勘察取样也是随机的。因此，只有在随机数学的基础上展开对岩土参数的分析统计，获得代表性的参数，理解和使用参数才有意义。

本文根据规范方法取得岩石抗压样本并进行试验，分别用规范提供的方法和提议的自助法对岩石单轴抗压强度进行参数估计，对岩样强度进行均值、置信区间及假设检验等统计推断，数据是基于严格方法取样和室内试验基础上的真实数据，其结果可供设计施工参考使用。对于一个采样，用规范方法只能计算出某个统计量但无法知道统计量的分布情况，但是求助于自助法可以模拟出统计量的近似分布。自助算法提供了规范的方法之外的另一种尝试，具有无需对总体分布作任何的假设，具有在高离散性、小样本时也可以使用的优点。