关于通过线圈某一面磁通量的讨论

陈敏华

摘    要：由于混淆面和面积的概念，人们不经意地会混淆通过线圈某一侧面的磁通量和通过每匝线圈同一侧面的磁通量.要消除这一概念上的混淆，必须认识到面和面积属于两个不同的范畴.

关键词：线圈;磁通量;面;面积;范畴

一、问题的提出

在人民教育出版社出版的普通高中课程标准实验教科书《物理》（选修3-2）中有这样一道练习题：

有一个1000匝的线圈，在0.4s内通过它的磁通量从0.02Wb增加到0.09Wb，求线圈中的感应电动势.如果线圈的电阻是10Ω，把一个电阻为990Ω的电热器连接在它的两端，通过电热器的电流是多大？

此题已经给出了通过线圈的磁通量，为什么还要告诉线圈的匝数？显然，教材编者混淆了通过线圈的磁通量和通过每匝线圈的磁通量.并且，根据这册教材的《教师教学用书》上所提供的解答，编者确实把“通过它的磁通量”当作“通过每匝线圈的磁通量”了.之所以会混淆这两个不同的概念，其原因是混淆了面和面积这两个概念.

面和面积有何区别？这正是这道题所引发出来的问题.

二、磁通量的定义

设某一矢量（vector）的位置分布为[V →]（[r]），其中[r]为位置矢量.[V →]（[r]）通过某一面（surface）S的通量（flux）Φ被定义为两个矢量的标积的面积分：

Φ=[SV →]（[r]）·[dA →]

式中，[dA →]为面S所对应的面积（area）[A →]的微分.

在对通量这一概念的理解上，特别要注意以下两点.

（一）通量一定是针对某一侧面来说的

通量的定义式是一个面积分，因此，它是针对面来说的.面是我们通过感官和大脑对物体观察的结果，是我们对物体抽象的结果.我们通过感官和大脑能从物质中抽象出所谓的性质、现象、状态等信息.在亚里士多德的《范畴集》中[1]，共列出了十大范畴，其中前四大范畴分别是物质（substance）、性质（quality）、数量（quantity）和关系（relation）.面是我们观察到的现象.显然，面属于性质这一范畴.我们把性质这一范畴下的诸如面、运动、电性、磁性、热等物理概念称为定性概念（qualitative concept）.

物理量是用来描述性质的，属于数量这一范畴.我们把数量这一范畴下的概念称为定量概念（quantitative concept）.因此，物理量是定量概念.

在物理教育中，我们必须向学生表明，面是定性概念，而面积是定量概念.但在有些教材中经常用表示面的符号S来表示面积.这是混淆面和面积概念的表现.严格地说，面积应该用A来表示.

这里我们所说的面包括曲面和平面（平面实际上是曲面的特例）.一个平面对应一条法线.具有连续转动法线的曲面称为光滑曲面.由有限多块不相交的光滑曲面连成的面称为简单曲面[2].这里所说的面指的都是简单曲面（包括平面）.

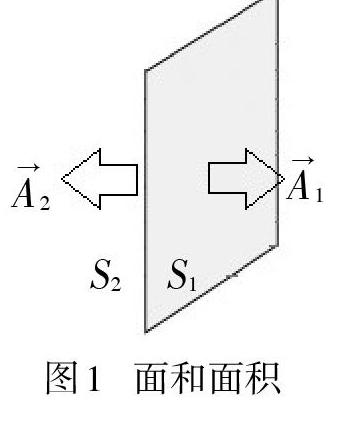
通常所说的“面”又包括两个侧面，而这两个侧面对应着正负号不同的面积矢量.举个简单的例子，对于一张纸（图1），它有左右两个侧面S1和S2，对应的面积矢量分别为[A1→]和[A2→].显然，[A1→=-][A2→].

对于图1中不同的侧面，某一矢量的通量刚好相差一个正负号.对于某一矢量，当这张纸转动180度后，它对某一侧面的通量就改变了原来的两倍.因此，在计算某一矢量的通量时，一定要明确是对哪个侧面来说的.

（二）通量一定是针对某一矢量来说的

前面已經说过，通量是两个矢量标积的面积分.在这两个矢量中，其中一个是面积矢量的微分.

如果这个面积分中的另一个矢量是速度[v→]，比如水流的流速，则其通量是水的流量（volume flow）：

Q=[Sv →]·[dA →]

如果这个面积分中的另一个矢量是电流密度[j→]，则其通量是电流（electric current）：

I=[Sj →]·[dA →]

如果这个面积分中的另一个矢量是电位移[D →]，则其通量是电通量（electric flux）：

Φe=[SD →]·[dA →]

如果这个面积分中的另一个矢量是磁感应强度[B →]，则其通量是磁通量（magnetic flux）：

Φm=[SB →]·[dA →]

对于匀强磁场，我们有：

Φm=[SB →]·[dA →]=[B →][Sd][A →]=[B →·A →]

另外，功率（能流密度矢量的通量）和力（动量流密度矢量的通量）也属于通量的概念.功率实际上就是能流，力实际上就是动量流.

三、拓扑学解释

在拓扑学中有这样一条原理：一个区域的边界不再有边界[3].具体地说，一个空间区域的边界是一个闭合的面，这个面不再有边界;一个面的边界是一条闭合的线，这条线不再有边界.

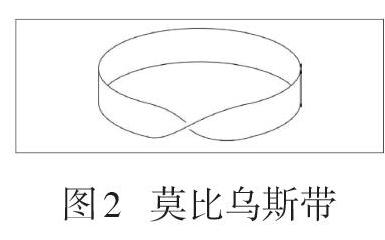
比如一个球体的边界是一个闭合的球面，这个球面不再有边界.再比如图1中的这张纸有左右两个侧面.因此，它有两条边界线.如果将它卷成一个圆筒，它仍有内外两个面和两条边界线.如果将它卷成如图2所示的莫比乌斯带（M?bius strip），它就只有一个面了，且只有一条边界线.实验表明，给用金属片制成的莫比乌斯带带上电，其电荷分布在整个“内外”表面上，不像法拉第圆筒实验中那样电荷只分布在其外表面上，而不分布在内表面上[4].

一个线圈实际上有两个侧面.所谓“通过线圈的磁通量”实际上是指“通过线圈其中一个侧面的磁通量”.根据拓扑学原理，每一独立的面只有一个闭合的边界，这个边界不再有边界.仔细分析我们会发现，n匝线圈的每一匝线圈的侧面的边界线是不闭合的，并没有单独构成一个侧面，而是构成整个线圈的一个侧面的一部分.因此，如果通过每匝线圈的某一侧面的磁通量都相等，则通过线圈的同一侧面的面积是线圈横截面面积的n倍;通过线圈的某一侧面的磁通量是通过每匝线圈的同一侧面磁通量的n倍.在一般情况下，通过线圈的某一侧面的磁通量是通过每匝线圈同一侧面磁通量之和.因此，通过线圈的某一侧面的磁通量又叫作全磁通（或磁通匝链数）[5].

在物理学中，我们通常用磁感线来形象地描述磁感应强度[B →].这样，也有利于我们直觉地理解通过线圈的磁通量.

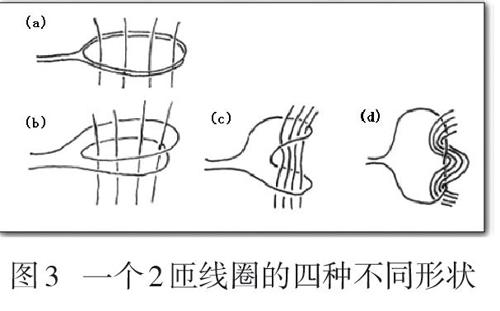
图3用四种不同的方式画出了一个2匝线圈.这四个图在拓扑学意义上是等效的[6].从图（d）中我们清楚地看出，一个线圈确实只有两个侧面（无论匝数有多少）;对于一个2匝线圈，每根磁感线都2次分别穿过它的其中任何一个侧面.因此，对于匝数为n的线圈，每根磁感线要穿过这个线圈的其中一个侧面n次，即磁感应强度[B →]对积分[SB →·d][A →]贡献了n次.

四、结束语

通量是物理学的重要概念，也是常用的概念，诸如功率、电流、电通量、磁通量、力等都属于通量的概念.

要正确理解通量这一概念，关键要区分面和面积这两个概念.面属于性质的范畴，面积属于数量的范畴.

要正确计算通过线圈的磁通量，我们还必须区分线圈的面和每匝线圈的面.我们不能混淆线圈的某一侧面和每匝线圈的同一侧面，否则就会混淆通过线圈的某一侧面的磁通量和通过每匝线圈的同一侧面的磁通量.上面我们提到的现行教材中的那道题和教师教学用书中的相应题解中的错误，就是这种混淆概念引起的.

参考文献：

[1]亚里士多德. 形上学[M]. 吕穆迪，译. 北京：北京时代华文书局，2014：83.

[2]谢树艺. 矢量分析与场论[M]. 北京：人民教育出版社，1978：26.

[3]YANG C N. Einsteins impact on theoretical physics[J]. Physics Today， 1980， 33（6）： 42-49.

[4]STEWART S. Flexible Faraday cage with a twist： Surface charge on a M?bius strip[J]. The Physics Teacher， 2007， 45（5）： 268-269.

[5]趙凯华，陈熙谋. 电磁学[M]. 北京：高等教育出版社，1985：462.

[6]HERRMANN F. Hochschulskripten Elektrodynamik[EB/OL]. （2015）[2019-12-27]http：//www.physikdidaktik.uni-karlsruhe.de/kpk_material.html

（本文中的一些观点是笔者在与德国Friedrich Herrmann教授、国内物理教育同行讨论中形成的，在此向他们表示衷心感谢）