T检验在体育统计应用中的一个注记
邹应军,甘胜进
(福建技术师范学院a.体育学院;b.电子与信息工程学院,福建福清 350300)
随着量化分析在体育活动评价中的重要性日益显现,体育统计迅速成为体育活动量化分析的一个有力工具,是从事体育教育与科研不可或缺的技能.许多高校甚至将《体育统计》这门课程纳入本科生必修课程,并配备操作软件EXCEL、SPSS、SAS等加以演示,取得了比较好的效果.然而,体育统计的理论基础毕竟是数理统计,涉及到复杂的数学公式和推导,这对不具备高等数学基础的体育科研与教育工作者来讲,极具挑战性,因此在体育统计应用过程中,常常出现跳过数据分布类型,直接利用软件来处理样本,这种做法既不符合数理统计规范,更不符合体育统计要求.再者,体育数据处理软件EXCEL虽然简洁,但在数据处理和统计图表绘制方面表现欠佳;SPSS是菜单式软件,不需要过多编写程序,图表输出十分美观,深受非统计类专业人士喜爱,但是其缺少灵活的数据分析;SAS虽然能通过手动编程灵活分析数据,但是其内存占用较大,并且SPSS、SAS均为商用软件,比较昂贵,但是大部分体育统计应用者利用破解版软件进行体育统计分析,这在知识产权保护方面存在潜在风险.相比之下,R软件完全共享免费,并且其强大的软件包足以满足统计分析要求,因此在统计学界扮演着举足轻重的角色,其详细使用说明请参看文献[1-2].本文以体育统计中常见的T检验为例,借助统计软件R来说明,利用T统计量作假设检验时需要注意的几个问题,尽管已有相关体育统计方面文献[3-8]对T检验做过注记,但是仅仅局限于依据定义概念对T检验作文字性描述.本文通过R软件产生的伪随机数,模拟利用T检验后的名义显著性水平来评价T检验效果,事实上利用统计模拟进行体育统计研究已有相关文献[9].
1 T检验相关理论
1.1 T分布基本概念
标准T分布的定义[10]为:假定独立同分布于标准正态分布,则服从自由度为n 的卡方分布,记为
通过T分布定义可得以下结论:①构造T分布的前提条件是总体为正态分布.②对于单样本T分布而言,如果总体不服从正态分布,那么T1的精确分布也不是t分布,此时特别对于小样本,如果仍然将T1看成t分布,那么统计推断效果将大打折扣.如果样本容量较 大,,依 据 中 心 极 限 定理可知,T1近似服从N(0,1),如果此时将T1看成t分布,那么对结果影响不大.③对于双样本T分布,如果两独立总体不服从正态分布,当两样本容量较大时,依据大数定律,再依据中心

1.2 T检验相关概念
T检验是在总体分布为正态情形下检验总体均值取值情况,或者两个独立齐性方差正态总体均值差异.前者为单样本T检验,后者为两样本T检验.由于双边检验和单边检验检验统计量一样,其主要差别为拒绝域,故本文重点讨论双边T检验.对于单样本T检验而言,

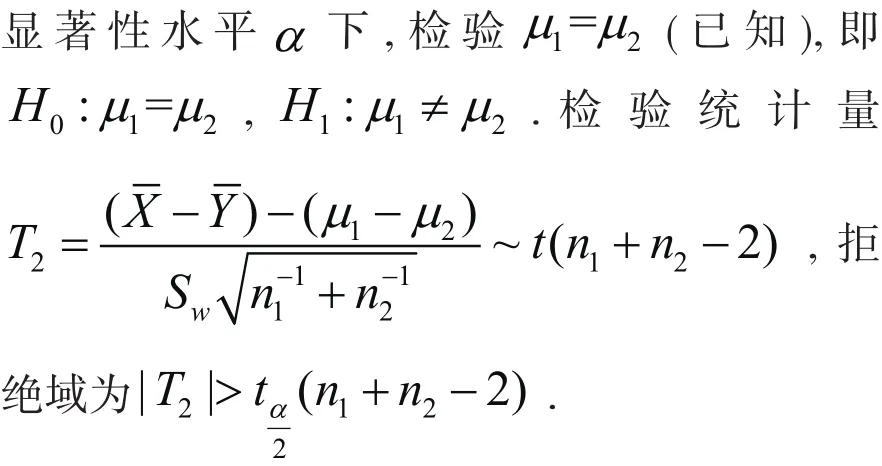
无论是单样本T检验还是双样本T检验,正态总体至关重要,判定样本是否来自正态分布,R软件一般采用Shapiro-Wilk正态性检验,例如社会体育专业某班35名学生《社会体育导论》考试成绩为:87 69 93 62 71 81 46 66 70 69 75 73 69 88 60 71 85 75 74 79 77 74 82 79 73 60 69 64 50 69 73 91 91 86 64.先用频率直方图和Q-Q图从直观上判断样本是否来自正态分布总体,其R语言命令为:
f<-c(87,69,93,62,71,81,46,66,70,69,75,73,6 9,88,60,71,85,75,74,79,77,74,82,79,73,60,69,64,50,69,73,91,91,86,64)
par(mfrow=c(1,2))
hist(f,pro=T,main="社体导论成绩频率直方图",xlab="成绩",axes = TRUE)
lines(density(f))
qqnorm(f)
qqline(f)

图1 频率直方图与正态Q-Q图
图1 为《社会体育导论》成绩频率直方图与Q-Q图,从左边频率直方图来看,数据不是完全对称,核密度曲线与正态分布密度函数有一定差异;从右边Q-Q图来看,数据点在直线附近波动,比较接近正态分布,这是从直观上得到结论.进一步通过R语言命令shapiro.test(f)来检验样本是否来自正态分布,其运行结果p值为0.4871,可以接受35名学生《社会体育导论》这门课的成绩来自正态分布的论断.
2 T检验统计模拟
为了证实上述结论,选取显著性水平α=0.05,在固定样本容量n下,100次蒙特卡洛模拟接受原假设的次数,如果原假设成立,则100次蒙特卡洛模拟大约有95次接受原假设,即接受原假设次数在95次附近波动,过大过小均不好,以上模拟再重复100次.在体育统计中,一般将n≥30作为大样本,为了方便比较,以下统计模拟中既有小样本,又有大样本.图2分别为总体X~N(4,1)和总体服从参数为1/4的指数分布下,采用单样本T检验次数的箱线图.其R语言程序代码为:
b<-matrix(0,nr=100,nc=3)
m<-0
for(n in c(20,30,200)){
m<-m+1
s1<-0
for(j in 1:100){
s<-0
for(i in 1:100){
a<-rexp(n,0.25)
#a<-rnorm(n,4,1)
t<-(mean(a)-4)*sqrt(length(a))/sd(a)
if(pt(abs(t),length(a)-1,lower=F)>=0.025)s=s+1 }
s1[j]<-s}
b[,m]<-s1}
图2左图为总体正态分布,在样本容量n分别为20、30、200下箱线图,发现均在95附近波动.右图为总体参数为1/4指数分布下利用T检验接受原假设次数箱线图,从中可知,在小样本下,表现得不令人满意,随着样本容量增加,越来越向95靠拢.左图中三种样本容量下平均数分别为94.96 、95.63 、94.70,右图中分别为92.15、 92.63、 94.58,显然正态分布总体下T检验效果更好,当样本容量比较大时,非正态总体下选用T检验效果也不错,这进一步证实了1.1节中结论②.

图2 正态分布总体与指数分布总体下,100次重复下,在各个样本容量100次蒙特卡洛模拟中,利用单样本T检验接受原假设次数的箱线图.
图3 分别为总体下,采用两独立样本T检验,接受H0次数的箱线图.其R语言程序与图2类似,故省略.左图为为两样本容量n1=n2,且分别为100、300、500下接受原假设次数的箱线图,从图中可知,其中位数均在95附近,采用T检验逼近的效果较好.右图为,从图中可知,接受原假设的次数的中位数均远远大于95,随着逐渐变大并且差别不大时,接受原假设次数的中位数向95靠拢.

图3 正态异方差总体下,100次重复下,在各个样本容量100次蒙特卡洛模拟中,利用两样本T检验接受原假设次数的箱线图.
图4为两非正态分布总体下,利用两样本T检验接受原假设的次数的箱线图,两非正态总体参数分别为1/20、1/4指数分布.左图为两指数分布总体样本容量相等,分别为100、300、500时接受原假设次数的箱线图,从中可以看出,均在95附近波动,检验效果比较符合预期.右图为样本容量不等,可以看出,检验效果极为糟糕,不过随着样本容量增大,两样本容量之间差别不大时,检验效果逐渐变好,这进一步验证了1.1节中的结论③.

图4 两不同参数指数分布总体下,100次重复下,在各个样本容量100次蒙特卡洛模拟中,利用两样本T检验接受原假设次数的箱线图.
3 结语
通过上述T检验理论分析以及统计模拟,在应用T检验进行体育统计应用之前,首先应该检验数据是否来自正态分布.如果正态性检验通过,便可应用单样本T检验.如果正态性检验未通过,当两样本容量较大时,若两样本总体方差相等或者两样本容量相等,可应用双样本T检验.

