RS柯西码编码算法改进研究

袁 炜，于 瀛，唐 聃

成都信息工程大学 软件工程学院，成都610225

1 引言

随着大数据产业的蓬勃发展，拥有巨大存储量的分布式存储系统得到了广泛的应用。数据存储量呈现指数级增长，对存储系统的数据可靠性提出了更高的要求。根据调查报告显示，在2015年，全球的存储数据量达到8.61 ZB，并且推断10年后，全球用于存储的服务器总量将增长10倍[1]。分布式存储系统的规模越大，节点越多，节点失效的概率也越大。因此，在节点失效的情况下，分布式存储系统需要使用一种数据容错技术来保障数据的可靠性，能够继续提供服务。

目前，常见的数据容错技术主要有多副本技术和纠删码容错技术。其中，多副本技术是在分布式存储系统中最为常见的容错技术。著名的云存储系统GFS[2]和Hadoop[3]都采用了此技术。多副本技术具有方案简洁、易于实施、构建成本低、便于扩展、无需任何运算等明显优势。但到了大数据时代，多副本技术需要消耗巨大的存储空间来维持其高容错能力。这导致其无法满足数据中心等大规模的分布式存储系统的需求。与多副本技术相比，在相同的容错能力下，纠删码容错技术的修复带宽和更新代价更小，存储效率更高。纠删码容错技术利用编码算法生成冗余数据，来实现对数据的容错。编码理论由Shannon C E首次提出，最初的应用主要在于网络通信领域，解决网络传输中的传输错误以及数据包丢失问题[4]。之后，Rizzo L 在1997 年的文献[5]中提出利用纠删码提高通信协议的可靠性的方法，也提出可将其应用在分布式存储系统中增强数据可靠性。

在分布式存储系统中，纠删码容错技术的研究热点主要在两大方面。一是阵列码。阵列码的编解码过程都只涉及二进制异或运算，具有构建方法简单，易于软硬件实现，运算效率高的特点。但阵列码的容错能力低以及对存储阵列尺寸有严格的要求，限制了阵列码的实用性。典型的MDS 阵列码中有二容错的EVENODD[6]码和X[7]码，三容错的STAR[8]码。但是目前为止还没有出现容错能力大于3的MDS 阵列码。第二便是RS码。基于RS码的纠删码容错技术是分布式存储系统容错的热门选择。分布式存储系统Ceph 以及前不久推出的Hadoop 3.0 都采用了基于RS 码的纠删码容错技术。RS 码是纠删码体系中唯一一种能够纠任意错的MDS码，在理论上容错能力不受限制且拥有最优的存储效率。然而RS 码的编解码过程中涉及多元有限域的运算，尤其是多元有限域的乘法运算，这使得RS码的计算复杂度高，严重影响了RS 码的编解码效率。复杂的计算使得计算代价过高，而这种计算代价是大规模分布式存储系统难以承受的。

针对RS 码的计算效率问题，学者们提出了一些优化方案。例如，通过查表的方式进行有限域的运算[9]；将多元有限域的运算转换到二元域上[10]；又或是通过指令集来加快多元有限域运算的GF-Complete[11]。其中最典型的方法是将多元有限域的计算转换到二元域上。从以上的优化方案可以看出，目前对RS 码的优化主要集中于对有限域运算的优化，对RS 码本体的优化相对较少。本文提出一种方法在RS 柯西码的基础上，根据柯西码的一些特性，减少计算量，并将柯西码阵列化，降低计算复杂度，最后，通过一种重复运算优化算法再次减少计算量，以此提高编码效率。该方法使得编解码过程只需异或运算和较少的计算量，这对提高RS 码在分布式存储系统容错领域的实用性有着重要意义。

2 RS柯西码

2.1 算法核心

1960 年Reed I 首次提出RS 码[12]。RS 码主要分为两种：一种是范德蒙码; 另一种是柯西码[13]。两者的区别在于其选择的生成矩阵不同，范德蒙码采用的是范德蒙矩阵，而柯西码采用的是柯西矩阵。所以，柯西码的算法核心在于柯西矩阵的构建。

定义1 设X 和Y 是有限域中的两个元素集。其中，X={x1,x2,…,xm} ，Y={y1,y2,…,yn}。若满足∀i ∈{1,2,…,m}，∀j ∈{1,2,…,n}有：

（1）xi+yj≠0；

（2）∀i,j ∈{1,2,…,m}，i ≠j，xi≠xj；

（3）∀i,j ∈{1,2,…,n}，i ≠j，yi≠yj。

称下列矩阵为柯西矩阵：

以上便是柯西矩阵的定义。

2.2 二进制矩阵

RS码的经典优化方法是利用二进制矩阵表示有限域元素进行运算[9]。这一方法极大地减少了有限域的运算复杂度，本文提出的方法需借助此方法将RS 柯西码进行阵列化。接下来对其进行简要介绍。

二进制矩阵的构造方法如下：

首先，求有限域元素的系数向量。多项式g(x)可以表示有限域GF(2w)上的所有元素，其中GF(2))，列向量v(x)=(g0,g1,…,gw-1)T称为多项式的系数向量。

然后根据定义2构造二进制矩阵。

定义2 对于任意元素e ∈GF(2w)，设α(e)是一个第i 列为xie mod p(x)的系数向量的二进制矩阵，其中p(x)是GF(2w)中度为w 的不可约多项式。

这些二进制矩阵拥有以下性质：

性质1 α 是GF(2w)到β(GF(2w))的同构，并且有：

（1）α(0)是一个全0矩阵；

（2）α(1)是一个单位矩阵；

（3）α 是一个单射；

（4）对于任意两个元素a,b ∈GF(2w)，有α(a+b)=α(a)+α(b)；

（5）对于任意两个元素a,b ∈GF(2w)，有α(ab)=α(a)α(b)。

在RS柯西码中，首先选取元素集X 、Y ，然后根据X 和Y 构建柯西矩阵，最后，将柯西矩阵中的有限域元素用二进制矩阵表示。如此便达到将有限域运算转换为二进制的异或运算的目的。

例如，在有限域GF(23)上，构建3 个数据块，2 个校验块的RS柯西码。

方案1 设选取的元素集为X={1,2},Y={0,3,4}，得到的柯西矩阵和替换后的柯西矩阵为：

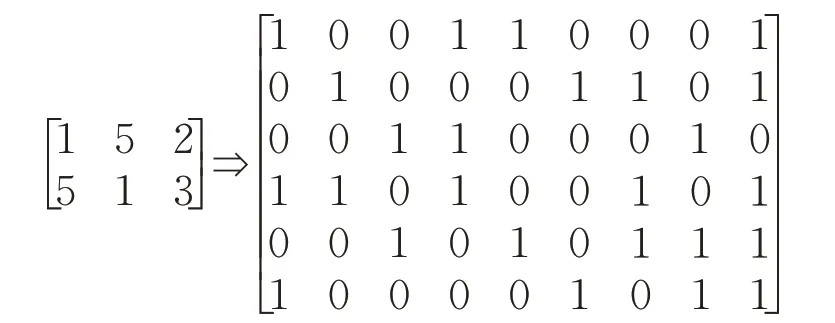
方案2 设选取的元素集为X={2,7},Y={0,1,4}，得到的柯西矩阵和替换后的柯西矩阵为：

替换后的RS柯西码的异或计算量等于替换后的柯西矩阵中1 的数量减去矩阵行数。以上给出的两个方案，方案1矩阵中1的数量为25，方案2矩阵中1的数量为37，方案2的计算量是方案1的计算量的163%。可见选取的元素集不同，RS柯西码的计算量也会大不相同。

3 RS柯西码优化算法研究

在文献[14]中，也提出选取的元素集不同，RS 柯西码的计算量会改变的观点，并对其进行较为深入的研究。为研究替换后的柯西矩阵中1的数量，根据柯西矩阵的性质，构建1 数量矩阵ONES(w)，其中，矩阵中的值ONES(w)i,j是二进制矩阵α()中1 的数量[14]。而在矩阵ONES(w)中选取n（数据块数量）行以及m（校验块数量）列，行列相交的值之和便是替换后柯西矩阵中1 的数量。但在文献[14]中，并未有选取元素集X 、Y 得到1 数量最少的柯西矩阵的合适方法，只能通过枚举的方法得到。在之后的已知文献中也未有提到过选取元素集的最优方法。

于是，本文提出一种优化方法：以一种贪心算法来选取元素集得到局部最优的柯西矩阵，再将其阵列化，并进行运算优化，使得计算量更加接近甚至超过最优柯西矩阵的RS柯西码。

接下来，介绍在有限域GF(2w)上，构建n 个数据块，m 个校验块的RS柯西码的贪心算法以及阵列化优化方法。

3.1 贪心算法

通过对矩阵ONES(w)的研究，发现矩阵ONES(w)沿斜率为-1 的斜对角线对称，并且第2i 、2i+1(0 ≤i ≤2w-1-1)行与第2j 、2j+1(0 ≤j ≤2w-1-1)列相交区域也沿斜率为-1的斜对角线对称，故而只需要保证X 、Y 在ONES(w)上半部分相加之和越小，则柯西矩阵中1 的数量越小。为方便描述，设有限域中元素e 对应的二进制矩阵中1的数量为We。

以下是贪心算法的详细步骤：

步骤1 在U1={0,1,2,…,2w-1-1}中，选取2w-2个元素{x1,x2,…,x2w-2}（除0以外），将这些元素归入X1，选取条件为：

步骤2 再将U1-X1 剩余的2w-2个元素归入Y1。

步骤3 在U2={2w-1,2w-1+1,…,2w-1} 中，选取2w-2个元素{x2w-2+1,x2w-2+2,…,x2w-1}，将这些元素归入X2，选取条件为：

步骤4 再将剩余的U2-X2 个元素归入Y2。

步骤5

（1）当m ＞n 时

①m ≤2w-1，如果n%2=0 ，则取num=n/2；如果n%2 ≠0，则取num=(n+1)/2。从X1 中选取num 个元素{x1,x2,…,xnum}归入X3 中，选取条件：

②n ≤2w-1，将Y1,Y2 合并成Y3，Y3={y1,y2,…,y2w-1} ，从Y3 选取n 个元素归于Y 中，选取条件：

（2）当m ≤n 时

①n ≤2w-1，如果m%2=0，则取num=m/2；如果m%2 ≠0 ，则取num=(m+1)/2。从Y1 中选取num 个元素{y1,y2,…,ynum}归入Y3 中，选取条件：；从Y2 中选取m-num 个元素{ynum+1,ynum+2,…,yn} 归 入Y4 中，选 取 条 件：。然后将Y3,Y4 合并成Y 。

②m ≤2w-1，将X1,X2 合并成X3，X3={x1,x2,…,x2w-1}，从X3 选取m 个元素{x1,x2,…,xm}归于X 中，选取条件：

步骤6

（1）当集合X 中的元素个数x_num 小于m 时，从G(2w)-X-Y 中选取 m-x_num 个元素{xx_num+1,xx_num+2,…,xm}归于X5 中，选取条件：

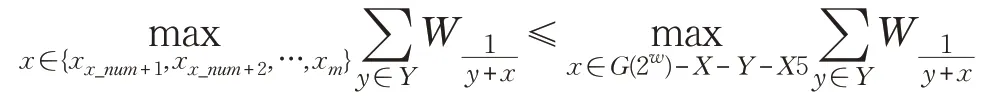
然后，将X5 合并入X 中。

（2）当集合Y 中的元素个数y_num小于n时，从G(2w)-X-Y 中选取n-y_num 个元素{yy_num+1,yy_num+2,…,yn}归于Y5 中，选取条件：

然后，将Y5 合并入Y 中。

这样就得到了最后的X 、Y 。本文算法虽在每一步都取1数量最少的元素，但是还无法保证最终总是取得最优解。

3.2 阵列化及其运算优化方法

根据3.1节的贪心算法，在有的情况下，还无法得到1数量最小的柯西矩阵。于是继续将其阵列化，并对阵列进行优化。将其阵列化既能够方便进行运算优化，又能够在译码时使用更简单高效的译码方法，避免使用复杂度高的RS柯西码的方程求解译码法。

以下是阵列化以及运算优化方法的步骤：

步骤1 设3.1节得到的元素集为X 、Y 。根据元素集X 、Y 构建柯西矩阵M1。然后将矩阵M1 中有限域元素用二进制矩阵表示，替换后的矩阵为M2。

步骤2 将RS 柯西码原来的n 个数据块，每一个切分为w 块。设这n×w 个数据块分别为D1,1,D1,2,…,D1,w,D2,1,…,Dn,w。

步骤3 计算校验块所需的数据块。

其中：

步骤4 进行阵列布局。为了不影响RS 柯西码的MDS 性质，将原本属于一个节点的抽象数据块放置于同一列上，条带大小依旧保持与原始的RS 柯西码一致。设排列后的阵列为A1。

步骤5 进行运算优化。

（1）R1,1,R1,2,…,R1,w,R2,1,…,Rm,w都是由D1,1,D1,2,…,D1,w,D2,1,…,Dn,w进行异或计算得到。因此，将D1,1,D1,2,…,D1,w,D2,1,…,Dn,w中每一个数据块都视作一个点。所有点组成点集P 。将R1,1,R1,2,…,R1,w,R2,1,…,Rm,w组成计算式集。

（2）遍历计算式集中的计算式，如有Da1,b1⊕Da2,b2⊕Da3,b3(0 ＜ai ＜n,0 ＜bi ＜m,i=1,2,3) ，则 将 点Da1,b1与 点Da2,b2，点Da1,b1与点Da3,b3，点Da2,b2与点Da3,b3连线。若是两点之间之前并没有连线，则进行连线，次数记为1；如果两点之间已有连线，则次数加1。

（3）当将计算式集中所有的计算式都连线完毕后，统计n×w 个点构成的图中两点之间的次数，保留次数最大的一条或多条线，如果次数都为1 则直接继续步骤（5）。

（4）在保留的线中，如果只有一条线，则直接将线的两个端点对应的数据块组成的计算式，作为替换式；如果有多条线，则从中选取不相交的线，将这些不相交的线的两个端点对应的数据块组成的计算式，作为替换式。

（5）利用替换式，替换阵列。最后，将替换式也视为点，加入点集中，重新进行步骤（2）。

（6）所有替换完成后，最终阵列为A2，将A2 中还依然保留的替换式保存到集合S 中。

当以上步骤都完成后，便完成了对RS 柯西码的优化过程。优化过程只需运行一次，之后的编码直接按照构建好的阵列以及替换式进行编码，无需重复执行。

4 具体实例

上一章对优化算法进行了系统的讲解，本章将采用典型的实例来进一步分析和说明本文算法。

例 以在有限域上数据块数为4，校验块数为3 的RS柯西码为例。接下来，分为两步简要介绍该RS柯西码的优化方法。

（1）贪心算法选取X 、Y

步骤1 构建有限域GF(23)的ONES(3)矩阵。

按照ONES(w)矩阵的构造方法，构造ONES(3)矩阵。得到矩阵如下：

柯西矩阵的X 中的元素不能与Y 的元素相等，所以矩阵ONES(w)对角线没有值。

步骤2 设X1 是从U1={0,1,2,3} 中选取2 个元素（除0 以外）组成的集合。即从矩阵ONES(3)的第0 行中的第1、2、3列中选取值最小的两列，将选取的列的序号加入到集合X1 中。X1={1,2}。

步骤3 将剩余的0、3列加入集合Y1。Y1={0,3}。

步骤4 在U2={4,5,6,7}中选取两个元素组成X2。即从矩阵ONES(3)的第4，5，6，7列中选取第0和3行相加值最小的两列，将选取的列的序号加入到集合X2中。X2={4,5}。

步骤3 进行阵列布局，得到阵列：

步骤5 Y2=U2-X2={6,7}。

步骤6 因为n ＞m，n=23-1，m%2=1，取num=2。从Y1 中选取2 个元素组成Y3。Y3={0,3}。从Y2 中选取1个元素组成Y4。Y4={6}。然后将Y3，Y4 合并为Y 。Y={0,3,6}。

步骤7 因为m=23-1。将X1，X2合并为X3。X3={1,2,4,5}。从X3 中选取3个元素组成X 。X={1,2,4}。选取条件为：

步骤8 集合Y 中的元素个数小于n，从G(2w)-XY 中选取1个元素组成Y5。Y5={5}。选取条件为：

然后将Y5 的元素添加入Y 中。

（2）阵列化并进行阵列运算优化

步骤1 根据贪心算法得到元素集X={1,2,4}和Y={0,3,5,6}构建柯西矩阵。并用2.2节所述的二进制矩阵替换矩阵中有限域元素，替换后的柯西矩阵为M2。

步骤2 取12个数据块，标记为D1,1,…,D1,3,D2,1,…,D4,3，计算冗余阵列：

步骤4 将数据块D1,1,D1,2,D1,3,D2,1,…,D4,3视为视为点。所有点组成点集P。将R1,1,R1,2,R1,3,R2,1,…,R3,3组成计算式集。

步骤5 遍历计算集，对点集中的点进行连线，记录次数。如图1所示。

图1 第一次连线图

图1 中只展示了部分次数较多的线条。可见连线次数最多为4，选择次数为4的不相交的连线（如红色线条）。然后将和作为替换式。将替换式对整个阵列进行替换。最后，将替换式也视为点，加入点集中。再次进行步骤5，直到连线次数最多为1。

步骤6 所有替换完成后，最终阵列为，将依然保留的替换式保存到集合中。如下所示：

优化结束，优化后的RS 柯西码直接根据阵列A2和集合S 就可以直接编码，类似于阵列码的编码过程。

5 性能分析与对比

对于纠删码而言，其关键在于编解码，本文主要研究的是RS柯西码的编码优化方法。本文提出的改进算法在确定了数据块数量和冗余块数量后，需要先进行贪心算法，阵列化以及运算优化一系列过程后，才能进行编码。在这一过程中，贪心算法需要消耗一定的计算资源，但是此过程在固定了数据块和冗余块数量的情况下只需要执行一次，之后的编码过程按照最后优化后的阵列进行异或运算编码即可。所以在分布式存储系统中，一次贪心算法所消耗的计算资源完全可以接受。

5.1 更高的编码效率

在有了二进制矩阵替换有限域元素的方法，将复杂的有限域运算转换为简单的异或运算，RS 柯西码的计算复杂度得到了一定程度的降低。但集合X 、Y 的不同，对RS柯西码的编码效率影响非常大。目前，并没有一个好的方法去得到最优集合X 和Y ，只能通过遍历得到，随着规模加大，得到最优集合的代价也会随之增加。也有采取随机的方式来选取集合X 和Y ，但得到的柯西矩阵的1的数量无法得到保证。图2展示了优化后的RS 柯西码与遍历最优RS 柯西码、随机RS 柯西码的编码所需异或数对比情况，并且以两种不同条件进行更全面的展示。图2（a）展示的是在保持校验块数为4，有限域为GF(24)的条件下，数据块数从4到9编码所需的异或数变化情况。图2（b）展示的是在保持数据块数为4，有限域为GF(24)的条件下，校验块数从4到8编码所需的异或数变化情况。从图中可以看出经过优化后的RS 柯西码编码所需的异或数远小于文献[14]的遍历最优RS 柯西码，并且选取集合X 、Y 的代价也相对较小。

图2 优化后的RS柯西码的编码所需异或数对比

编码效率不仅能够通过编码所需的异或数来体现。通过编码时间也能更直观地反应编码的效率。图3与图4 分别展示了优化后的RS 柯西码与EVENODD码、STAR 码分别对1～10 MB 的文件进行编码的编码时间对比情况，并分为数据块数为5 和7 分别进行对比。从图中可以看出经过优化的RS柯西码的编码时间与以编码效率著称的阵列码中的代表EVENODD码和STAR码相差不大，甚至有一些优势。并且对于EVENODD码和STAR码，容错超过3便失效了。可见优化后的RS柯西码编码效率有了很大幅度的提升。

图3 优化后的RS柯西码与EVENODD码的编码时间对比

图4 优化后的RS柯西码与STAR码的编码时间对比

5.2 更简单高效的译码方案选择

本文提出的优化方法虽然主要是提升编码效率，但是对RS 柯西码的译码也有积极的影响。未优化前的RS 柯西码虽然通过将有限域的运算转换为异或运算，对译码的效率有所提升。但其在译码过程中仍未消除需要对矩阵进行求逆这一复杂的操作，这也导致译码效率无法得到更有效的提升。经过优化后的RS柯西码在编码的过程中更贴近于阵列码的编码过程，因此可以选择使用更简单高效的译码方法，不需要对矩阵进行求逆。例如文献[15]中提出矩阵译码方法，在阵列码中的应用最佳，利用该方法对优化后的RS 柯西码进行译码。省去对矩阵求逆这一复杂操作，且译码过程只涉及异或运算，译码效率将有大幅度的提升。

6 结束语

本文在分析RS 柯西码算法存在的缺陷的基础上，提出利用贪心算法和二进制矩阵对RS柯西码编码的改进算法。改进后的RS柯西码采用贪心算法减少了柯西矩阵中1 的数量，一定程度上降低了计算量，提高了编码效率。同时，在改进的RS 柯西码中利用二进制矩阵进行阵列化，降低计算复杂度，并加以运算优化，再次提升编码效率，从而使算法能够跳出局部最优的局限，将编码效率提升至接近甚至超越最优解。

通过仿真实验和分析可知，改进算法不仅大幅度减少了计算量，有着较高的编码效率，并且对译码来说，经过阵列化的编码过程能够选择更为高效简单的译码方法，一定程度上提高译码效率，算法有较高的实用性。