数据驱动的跨临界CO2热泵多目标优化设计

李恩腾，徐英杰，谢小东，范伟

（浙江工业大学机械工程学院，浙江杭州310023）

随着人们生活品质的提高，家用热水的需求量也在不断增加，然而在国内热水超过90%都是直接燃烧化石燃料加热，造成了严重的环境污染与破坏[1-2]。因此，高效清洁的跨临界CO2热泵热水器具有较大开发价值。CO2具有的天然环保特性以及跨临界CO2热泵系统对于加热高温热水表现出来的巨大优势，使得跨临界CO2热泵热水器在住宅中的应用具有广阔的前景[3]。然而跨临界CO2热泵热水器也存在一定的问题；首先，跨临界CO2热泵热水器的投资成本太高，远远高于电、燃气、太阳能热水器的成本，很难被普通用户所接受[4]；其次，跨临界CO2热泵热水器的储热水箱会占用较大的室内空间，给用户的使用带来很大不便。因此，CO2热泵热水器需要综合考虑经济性和实用性，对设备的性能和设计进行优化改进。

Lorentzen 与Pettersen[5-6]率先对CO2跨临界循环进行了研究，研究表明CO2热泵系统在性能上可以达到较高的性能系数（COP），能满足高温热水生产的需要，并且比电热水器和燃气热水器减少约75%的能源消耗；此外对于未来环境问题而言，也避免许多不确定性因素的产生。Saikawa 和Koyama[7]从理论上研究了各种制冷剂单级压缩热泵循环的COP 上限，发现制冷剂CO2具有最高的COP。Qi 等[8]进行了一项评估跨临界CO2空气源热泵热水器最佳排气压力的实验研究，以实现系统的最佳性能。Nawaz等[9]研究了CO2热泵热水器水循环速率对水箱中水温分层的影响，表明这是可以提高CO2热泵系统性能的关键因素。Fernandez 等[10]发现跨临界CO2热泵热水器的热水在水箱中长期储存，由于热传导的影响会使中温水区域扩大导致系统性能下降。为了解决该问题，Ohkura等[11]采用了从跨临界CO2热泵水箱侧面提取温水的方法来克服系统性能下降的缺点，同时使用数值模拟分析了这种跨临界CO2热泵改进水箱的加热系统性能，并通过实验验证其有效性。以上研究的重点主要集中在优化跨临界CO2热泵系统的性能系数，然而单从性能这一参数上进行优化，可能会造成㶲损和经济成本的增加，所以对跨临界CO2热泵进行多目标优化具有重要的现实意义。

Rezayan 和Behbahaninia[12]对CO2/NH3级联热泵循环进行了㶲分析和经济性优化，在制冷量、环境温度和制冷空间温度约束下，以最大限度地降低该级联系统的总年度成本。结果表明，与基础的设计系统相比，该优化系统的总成本降低了9.34%。虽然该系统对㶲进行了分析，但仅对单一的经济成本进行优化，无法满足用户的多元化需求。Fazelpour和Morosuk[13]从跨临界CO2热泵的性能和成本角度进行了优化分析，采用经济器作为单级跨临界CO2热泵的辅助装置降低了14% 的最终成本。Aminyavari 等[14]采用遗传算法对CO2/NH3级联制冷系统的㶲效率、经济性和环境影响进行了系统优化。优化结果表明，对于制冷量为50kW的工厂案例，Pareto 前沿选择的最佳设计㶲效率为45.89%，年度总成本为277070USD/a；但是该优化过程的热力学模型复杂，优化的计算量大。因此，Khanmohammadi等[15]采用了人工神经网络的方法来简化热力学模型，以制冷量和年度成本为目标对跨临界CO2制冷循环进行热经济优化，最终增加了4.6%的制冷量，降低了60.6%的年度成本。

如上所述，跨临界CO2热泵无论是对性能目标进行改进，还是对性能系数、㶲效率、经济成本等多目标进行优化都未涉及实用性的分析，然而，对于实用性的优化有重要的现实意义。因此，本文基于BP 神经网络与NSGA-Ⅱ算法以跨临界CO2热泵的总经济成本与水箱体积为目标函数建立了跨临界CO2热泵的优化设计模型，并通过对常用CO2热泵住宅案例进行优化为用户提供最优设计方案。

1 系统介绍及模型建立

1.1 跨临界CO2热泵模型建立

跨临界CO2热泵系统主要由压缩机、气冷器、蒸发器、膨胀阀、阀门、水泵、水箱等部件组成，结构如图1 所示。其循环工作原理是，CO2在蒸发器中吸收空气热量被蒸发为低温低压的气体，然后在压缩机中被加压成高温高压的超临界状态，通过气冷器将热量释放出来用于热水加热，加热的热水储存在保温水箱中，供给于用户使用，在气冷器中被冷却了的CO2经由膨胀阀节流降压再进入蒸发器中吸收空气热量蒸发，从而构成了跨临界CO2热泵循环。CO2跨临界压缩循环的温熵图如图2 所示。其热力循环数学模型见式(1)～式(6)。

图1 跨临界CO2热泵循环原理

图2 跨临界CO2循环温熵图

其中，CO2压缩机的等熵效率ηS是关于压比的多项式函数[式(3)][16]。

其中，p1、p2为吸排气压力。制热量、COP、制冷量分别由式(4)～(6)表示。

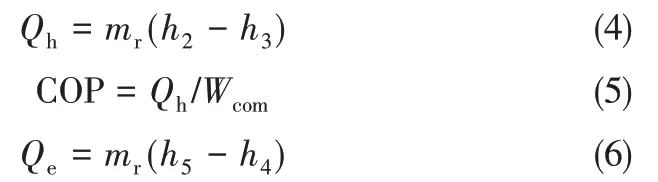
气冷器换热温差由式(7)计算。

对于该CO2热泵热水加热系统，基于电网的峰谷电价制，热泵机组可在夜间（低电价时段）运行生产热水储存在水箱中用于用户的热水使用，因此体积越大的水箱能储存更多的热水，意味着运营成本就越低。然而更大的水箱也会导致占用更大的室内空间、更大的水箱投资成本以及水箱散热面积增大所带来的漏热损失的增加，从而导致用户安装的不便以及成本上升；并且，热泵自身的设计参数，如气冷器换热器温差，也会对热泵系统的投资成本、运营成本产生影响。因此，更小的经济成本与更小的水箱占用空间是存在冲突关系的两个目标。所以，对于CO2热泵热水加热系统而言，其设计工作还存在很大的优化空间。

1.2 神经网络模型的建立

由于跨临界CO2热泵热物理模型的复杂性，本文将采用神经网络的方法建立CO2热泵的热力学性能预测模型。人工神经网络技术可以被认为是一种回归技术，它可以表示自变量和因变量之间更高的非线性关系[17]。本研究采用的神经网络技术是前馈反向传播（BP）神经网络。BP 神经网络模型通常由输入层、隐藏层和输出层组成，如图3所示。隐藏层可以存在多个，然而，已经证明在有足够数量的神经元情况下，一个隐藏层足以逼近任何连续的函数[18]，并且输入或隐藏层可具有偏置神经元。在不同层的神经元之间具有连通性，每一层中的神经元与其输入层和输出层的所有神经元节点相连。本研究的输入层为气冷器换热温差（Δtm），输出层为气冷器压力（pgc）、性能系数（COP）、压缩机功率（Wcom）以及制冷量（Qe）。隐藏层的节点值由以下传递函数[式(8)]计算。

图3 BP神经网络拓扑结构

其中，Ni为隐藏层第i个神经元节点；X为输入层神经元节点，即气冷器换热温差（Δtm）；ω1i和b11i为输入层与隐藏层之间的权重与阈值。同样输出层的节点值由以下传递函数[式(9)]计算。

其中，Yj为输出层第j个神经元节点；ωij和b2ij为隐藏层与输出层之间的权重与阈值。每个输出神经元的误差是预期输出和实际输出之间的差值平方，定义如式(10)所示。

其中，D为实际的目标值，输出层与隐藏层的误差信号分别如式(11)、式(12)所示。

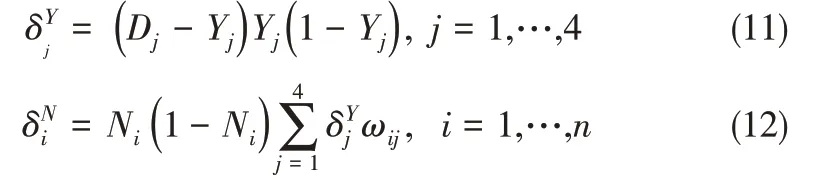
输出层与隐藏层之间的权重以及输入层与隐藏层之间的权重如式(13)、式(14)求得。

其中，α为学习率，权重的更新如式(15)、式(16)。

其中，k为误差传播的迭代数；β为权重更新的动量参数。同理可得偏置的更新如式(17)、式(18)。

首先，根据热力循环数学模型，在不同的输入参数下对跨临界CO2热泵进行性能模拟分析以获得大量的驱动数据，然后经由BP 神经网络构建跨临界CO2热泵的热力学预测模型，训练流程如图4 所示，初始参数见表1。通过网络的迭代训练得到预测模型，具体情况如图5所示。

采用均方根相对误差（RMSE）作为神经网络预测模型效果的评判标准[式(19)]。

图4 BP神经网络训练流程

表1 神经网络建模初始参数

对气冷器压力、COP、压缩机耗功以及制冷量各参数测试集的预测结果进行误差分析，其结果见表2。

通过误差分析，气冷器压力的均方根相对误差最低，仅为0.65%；COP、压缩机耗功与制冷量虽然都存在个别样本点的误差偏大，但均方根相对误差也能达到较高的精度。因此，该神经网络预测模型能满足预测精度要求，且没有产生过拟合现象，因此其泛化能力较高。

表2 输出参数均方根相对误差比较

图5 输出参数测试数据预测值与目标值的比较

1.3 经济评估模型的建立

1.3.1 投资维护成本

热泵系统的总投资成本等于各部件的投资成本之和，对于水泵的投资成本设定为定值Zhump=240USD，其余每个部件成本（Zk）由以下成本函数[式(21)～式(26)]计算[19]。

其中，D、H、δ分别为水箱的直径、高度以及保温层的厚度；pgc与Wcom来源于神经网络的预测结果，换热器的成本为换热面积的函数，换热面积可通过式(27)求出。

其中，U是整体的换热系数，一般估计在1.5～2.5kW/(m2·K)的范围内[20]；Q和Δtm分别为换热量与换热温差。

在工程经济学中，投资成本的评估通常要进行年化，时间间隔为一年，并且使用资本回收系数（CRF）获得相应的成本，其可以由式(28)[21]确定。

其中，i和n分别是年利率与系统的运行寿命，见表3。考虑维护成本，即维护系数φ=1.06，总投资维护成本为式(29)。

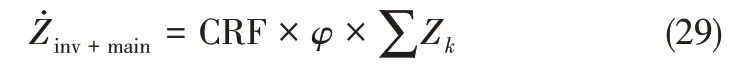
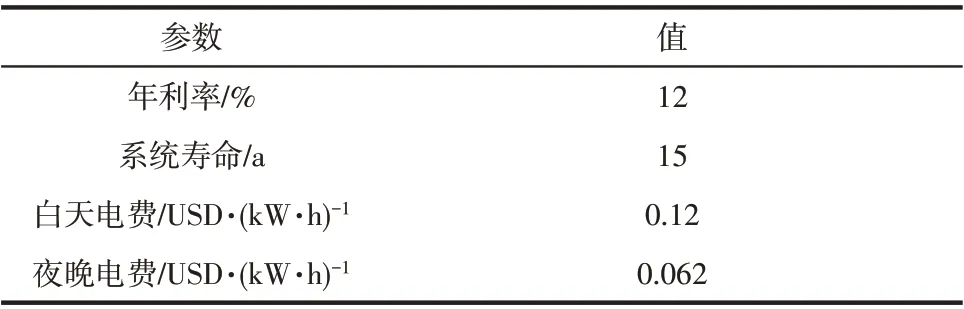
表3 经济参数

1.3.2 运营成本

跨临界CO2热泵系统的运营成本主要来源于压缩机与水泵的电能消耗，而以上的功耗与水箱的尺寸以及热损失有关，水箱结构为圆柱形，其水箱的容积由式(30)求得。

在一天中水箱热量的损失量由式(31)求得。

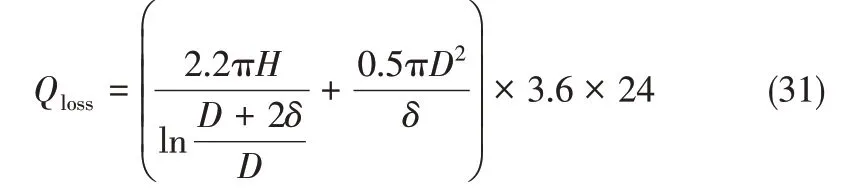
其水箱采用的保温材料为聚氨酯，热导率为0.022W/(m·K)，对于一天所需的热水热量由式(32)～式(34)求得。

其中，Vdemand为一天热水所需的体积；ρwater和cm分别为水的密度与比热容；Δt为水加热的温差。在本文中，水泵的功率被设定为Wpump=657W，因此白天与夜晚的电力成本由式(35)、式(36)求得。

1.3.3 环境成本

由于热泵系统的电力消耗所造成的CO2排放，将会带来排放罚金，由式(38)求得。

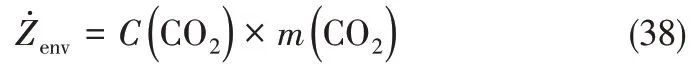
其中，C(CO2)为CO2排放罚金的单价，通常取在0.022～0.130USD/kg 的范围[22]，在本文中设定为0.05USD/kg；m(CO2)为CO2的排放量，由式(39)求得。

其中，μ(CO2)是电网发电产生CO2的转换系数，取为0.968kg/(kW·h)。

该经济模型的建立基于以下假设：

①系统运行稳定，且热水需求量保持不变；

②所有的连接管路没有热量损失；

③整个模型的计算周期为一天（24h），且环境温度保持不变；

④系统优先在夜晚（低电价时期）运行，并装满整个水箱，水箱储存热水不够再在白天运行。

2 优化方法与案例分析

NSGA-Ⅱ是Deb 等[23]提出的一种基于Goldberg思想的帕累托最优概念多目标优化遗传算法。与传统遗传算法相比，该算法引入了一种基于Pareto和非支配解概念的新选择机制。选择机制通过个体之间的支配与非支配关系对种群进行排序，具有较高非支配等级的个体被选择的概率越高。对于同一非支配等级的一系列个体，拥挤距离越大，被选择的概率越大。最后，根据非支配序与拥挤度算子得到了多目标优化的Pareto解集。一般来说，多目标优化数学模型可以用式(40)～式(43)描述。

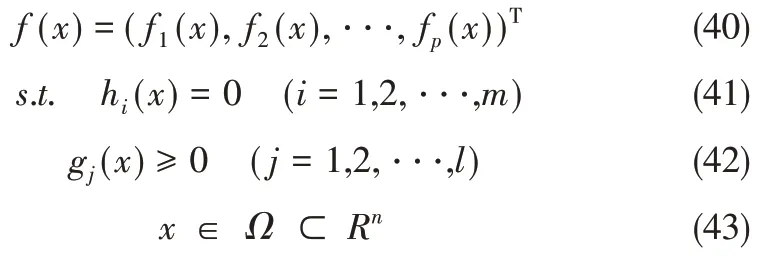
其中，x∈Rn为决策变量；Ω为可行域；hi(x)和gj(x)均为约束函数；f(x)为p个目标组成的目标函数向量。

本文中，考虑的目标函数为最小化的总经济成本目标[式(20)]以及最小化的水箱容积目标[式(30)]。并且为了选择对目标函数具有实质影响的主要参数，进行了参数研究，将气冷器换热温差（Δtm）、水箱的直径（D）、水箱的高度（H）以及水箱保温层的厚度（δ）作为优化的设计参数，其各自的变化范围见表4。以及本案例的研究是对于6.45kW的家用CO2热泵热水器最优化设计，其案例数据见表5。

表4 设计参数变化范围

表5 案例数据

3 结果与讨论

为了解决优化问题，随机产生一个父代种群，计算所有个体的目标函数值，再进行非支配排序和拥挤度计算，将非支配序与拥挤度距离组成拥挤度算子进行选择，得到非支配前沿个体；然后对种群进行交叉、变异操作，产生子代种群；最后将父代与子代种群结合，选出最优秀的种群替换父代种群。具体的优化过程如图6所示。

通过NSGA-Ⅱ算法程序的优化求解，得到最终的优化结果，其程序的调试参数见表6。研究的跨临界CO2热泵系统总经济成本与水箱容积两个目标存在明显的冲突关系如图7 表示，从Pareto 前沿图中可知，水箱容积从0.02m3变化到0.52m3，导致了总年度成本从914USD/a 变化到984USD/a。而图中A选择点为仅考虑水箱容积目标最小化时的方案点，其水箱容积只有0.02m3，然而相应的总年度成本高达984USD/a；同样B点为仅考虑总年度成本目标最小化时的方案点，其总年度成本为914USD/a，而导致的水箱容积为0.52m3。之所以在Pareto 非劣解集中出现了高于案例需求量0.5m3的解方案，是因为水箱存在热量的损失。

图6 NSGA-Ⅱ优化算法流程

表6 优化程序的调试参数

图7 跨临界CO2热泵系统多目标优化的Pareto前沿

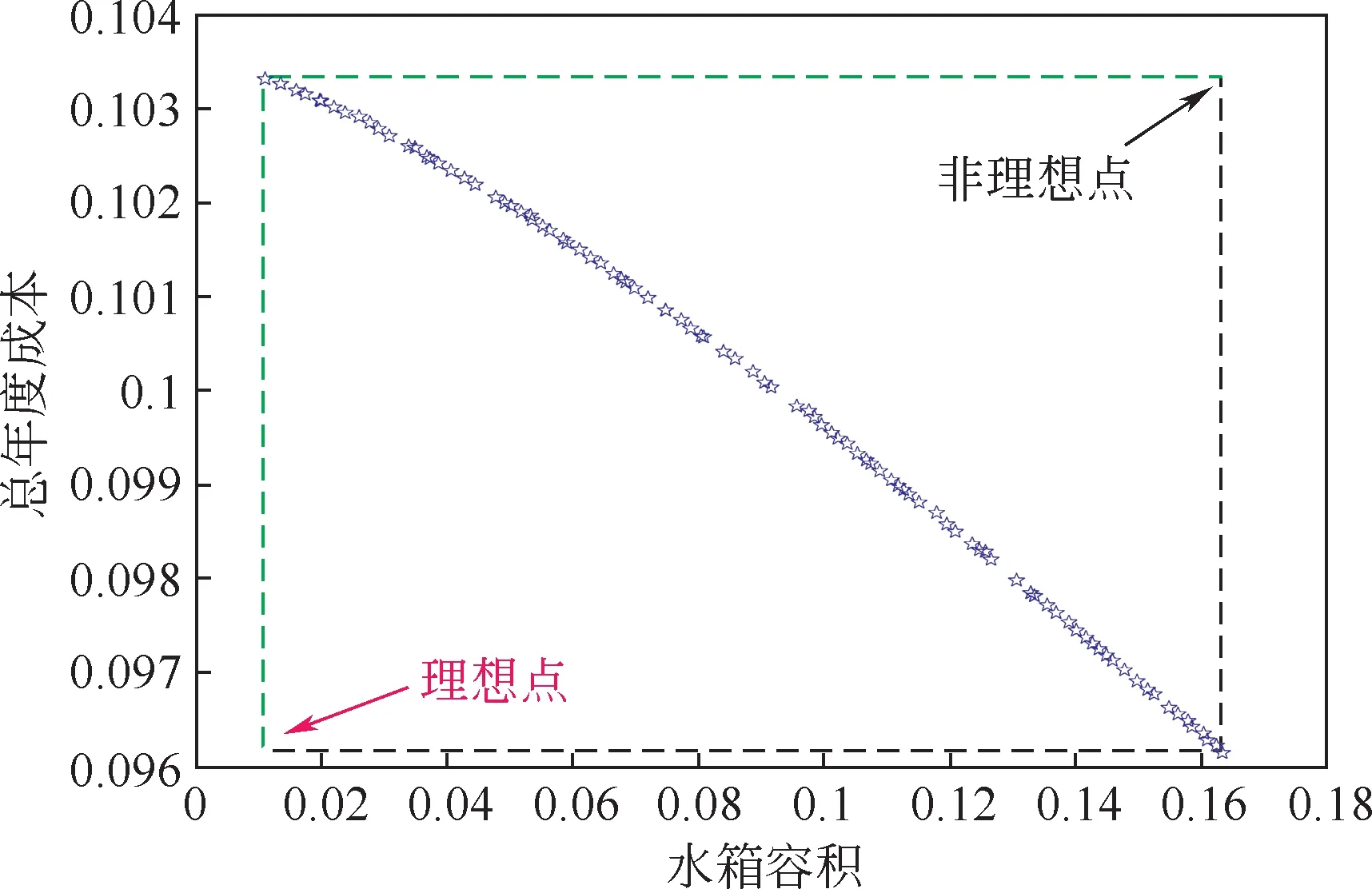
图8 跨临界CO2热泵系统多目标优化的量纲为1化Pareto前沿

对于多目标优化问题，从Pareto前沿获得的所有非支配解均可以被选为最优的方案解，然而对于实际的工程问题只能选择一个最优的解方案。近年来，在相应领域的研究中，各种决策方法被用于选择Pareto 前沿中的最优解，其中TOPSIS 决策法具有鲁棒性强的特点得到广泛应用[24]。TOPSIS 决策法的中心理论是找到距离理想方案点最近且距离非理想方案点最远的点[24]，理想点为点A与点B在各自最优方向上的交点，如图8中所示，同样非理想点为点A与点B在各自最差方向上的交点。

对于大多数的多目标优化问题，其目标的物理量纲不同（本文中总年度成本是USD/a，而水箱容积是m3），因此在对优化结果进行TOPSIS方法优选之前，还应对目标函数的值进行量纲为1化。采用欧式方法[25]对本文的Pareto 非劣解集进行量纲为1化，其结果如图8 所示。然后通过计算得到Pareto前沿上所有解到理想点的距离（d+），以及到非理想点的距离（d-），通过其接近度[d-/(d-+d+)]标准，得到接近度最大的方案解，即综合考虑了两个优化目标得到的最优解，如图7中所示。其该点的水箱容积与总年度成本分别为0.235m3与958.1USD/a，相应的最优设计参数见表7，以及相应的性能经济优化参数见表8。

为了分析设计参数对于优化目标的影响，得到如图9 所示的Pareto 种群设计参数分布。从图中可知，保温层厚度大致平均分布在65～75mm较小范围内，这是因为保温层的厚度对于水箱的设计有最佳的厚度区域，保温层过薄保温效果差，保温层过厚对于保温效果提升不大，反而造成了投资成本快速上升。而水箱的高度分散的分布在0.50～0.83m的范围内，水箱的直径也均匀分布在0.30～0.93m的范围内，说明了以上两个设计参数对于优化目标的影响较大，具有直接的作用。而气冷器的换热温差集中在14.5℃的左右，说明了气冷器换热温差对于优化目标而言影响较小。

表7 TOPSIS 优选点的系统设计参数

表8 TOPSIS优选点对应的性能经济参数

4 结论

本文对跨临界CO2热泵系统进行了实用性与经济性为目标的优化设计分析，通过BP 神经网络构建跨临界CO2热泵的预测模型，再使用NSGA-Ⅱ优化算法对以上目标的跨临界CO2热泵系统进行优化，可获得以下结论。

（1）获得了精度高、无过拟合现象的跨临界CO2热泵神经网络预测模型，能快速、准确地进行数据的预测。

（2）对本文中案例进行优化分析得到Pareto前沿，通过TOPSIS 决策法选出最优的设计方案为水箱体积0.235m3、总年度成本958.1USD/a。结果表明，所选的最优方案具有占用空间小且总经济成本小等优点。

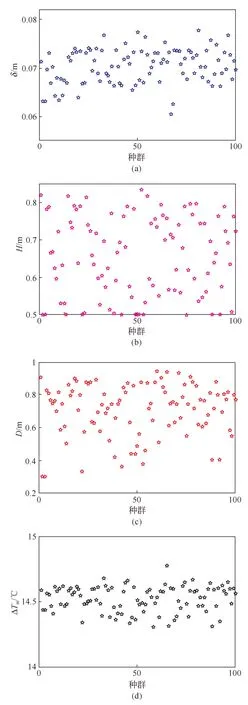
图9 Pareto种群设计参数分布

（3）水箱保温层厚度对于优化目标的影响主要集中在一个较优区域，水箱的直径与高度对于优化目标的影响较大，而气冷器换热温差对于优化目标的影响较小。之后的研究可对设计参数的选取再进行优化改进以获得影响更有效的参数。

符号说明

COP—— 性能系数

D—— 水箱直径，m

H—— 水箱高度，m

h—— 焓，J/kg

mr—— CO2流量，kg/s

pgc—— 气冷器压力，kPa

Qe—— 制冷量，W

t—— 温度，℃

Δtm—— 气冷器换热温差，℃

V—— 水箱容积，m3

Z—— 成本，USD

δ—— 水箱保温层厚度，mm

下角标

com—— 压缩机

day—— 白天

demand—— 需求

e—— 蒸发器

env—— 环境

exv—— 电子膨胀阀

gc—— 气冷器

in—— 进口

ins—— 水箱保温层

inv—— 投资

loss—— 损失

main—— 维护

night—— 夜晚

op—— 运营

out—— 出口

pump—— 水泵

tac—— 总年度成本

water—— 水

wt—— 水箱