固废破碎料涡电流分选过程中有色金属弹射角影响因素分析

魏红港，冉红想，王晓明

1北矿机电科技有限责任公司 北京 100160

2北京矿冶科技集团有限公司 北京 100160

20 世纪以来，电子信息产业快速发展，层出不穷的技术创新与持续的市场需求加速了电子产品的更新换代，同时产生了大量的电子废弃物。电子产品废弃物中含有大量的有色金属、黑色金属、塑料、玻璃以及一些可重新利用的零部件，这些二次资源是与自然资源同等重要的“城市矿山”。涡电流分选是固废机械化处理工艺中最关键的技术，适用于导电率不同物质间的分离，在国外广泛应用于城市垃圾中废杂金属的分离回收再利用。

对涡电流分选技术的研究，已经有百余年的历史，1889 年 Thomas Edison 申请了分离有色金属和非金属的交变磁场电涡流分选技术专利[1]。随着磁性材料的发展，美国和德国率先出现了工业应用的涡电流分选机[2]。近 20 年来，由于涡电流分选机的特殊用途，使得学者们对涡电流分选技术的研究取得了许多成果。Rem 等人[3-4]用微分方程描述了非磁性颗粒在变化磁场中的运动轨迹，并给出了磁场强度的计算方程。Lungu 等人[5-6]建立起 VDESC 和 SDECS 2 种涡电流分选机颗粒所受到涡流力。邓少华[7]建立了不同形状物料涡流力模型。近年来，社会各界对环保和资源循环利用日益重视，采用涡流分选技术回收电子产品破碎料中有色金属方面的研究可见报导更多[8-12]。

笔者以带式涡流分选机为研究对象，采用有限元仿真分析方法，旋转磁辊有效磁场强度计算公式，在此基础之上将磁辊磁场和导电体内部感生涡流形成的磁场视为 2 个相反的磁极，推导出圆形金属片涡流力模型，阐明弹射角可作为物料分选难易程度的量化指标，计算分析了影响弹射角的因素。

1 涡电流分离原理

涡电流分选原理基于 2 个物理学定律，即电磁感应定律和毕奥-萨伐尔定律：金属在变化的磁场中会产生感应电场，电场又能激发出磁场。如图 1 所示，有色金属导体在传送带静摩擦力f的带动下沿传送带方向运动，当其进入高速旋转的 N-S 极交替磁系所形成的交变磁场区域时，导体磁通量发生变化，使导体内部产生闭合环形感应电流，称其为涡电流。涡电流又会在导体内激发出相应的磁场，该磁场与旋转磁系磁场极性相反，使磁系与有色金属导体之间产生排斥力F。

图1 涡电流分选原理Fig.1 Principle of eddy current separation

有色金属导体随传送带继续沿滚筒旋转方向运动，其与磁系的距离越来越近，位置点的磁场强度越来越大，导体所受的涡电流斥力F逐渐增大，弹力N和静摩擦力f逐渐减小。当导体所受的涡电流斥力F在竖直方向分量等于导体块重力G的瞬间，导体块被弹射出去。不同物料由于导电率的不同，弹射点和弹射路径都不相同，从而实现不同导电率物料的分离。

2 磁辊磁场分析

磁辊是涡电流分选机的核心部件，是分选的原动力和基础，笔者对同心带式涡电流分选机磁系进行建模分析。磁辊的主磁极为圆周方向 N-S-N 交替排列布置结构，相邻磁极之间有一个辅助磁极来提高磁场强度，磁系的中心是圆形铁芯，磁系结构参数及所选用的磁性材料性质分别如表 1、2 所列。

表1 磁系结构参数Tab.1 Parameters of magnetic system

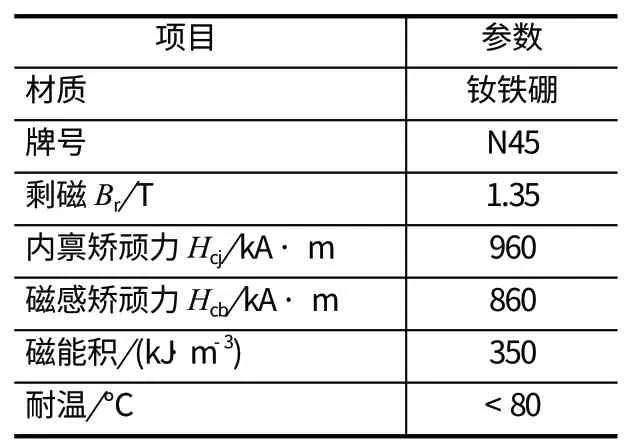
表2 磁性材料参数Tab.2 Parameters of magnetic material

利用有限元分析软件对涡电流分选机磁系进行二维磁场分析，做出磁系整体磁场强度等值线，如图 2所示。

图2 磁场等值线Fig.2 Contours of magnetic field

由图 2 可知，磁辊近表面磁场等值线有峰有谷，波峰位置在相邻磁块贴合面的顶点，波谷位置在辅助磁极中心截面处；随着到磁系表面距离的增加，磁场等值线波动幅度变小，当距离增大到一定程度后，磁场等值线呈圆形分布在磁系的周围。磁场强度最大的地方主要集中在磁辊外表面，由于模拟是建立在静态条件下，同一半径磁场强度有高有低，然而在磁辊旋转过程中，由于转速较快，低磁场区域会被高磁场区域覆盖，在磁辊表面形成分布近似均匀的磁场。

分别做出距离涡电流分选筒表面 0～25 mm 的磁场分布图，如图 3 所示。由图 3 可知，筒表磁场峰值为 750 mT，谷值为 600 mT，但是距离筒表 25 mm 处磁场强度基本不变。

图3 圆周方向磁场强度分布Fig.3 Distribution of magnetic field intensity along circumference

磁系外围的磁场强度随着距涡流分选磁系表面距离的增大而逐渐减小，超过一定值后，磁辊外围的磁感应强度值将变得很小，且各位置处径向磁场强度随着距离的增大而逐渐相等。因此，在电涡流分选过程中，要尽量使有色金属块贴近电涡流分选机的表面，使其在较强的磁场中获得较好的分选效果。

为了计算导电体感生涡电流激发的磁场，必须获得磁辊磁场，涡电流分选机磁辊外部空间磁场强度可参考 Rem 等人给出了圆柱坐标系 (r，φ，z) 下涡电流分选机的磁场强度计算方程[3-4]：

式中：bn为傅里叶系数，可以通过测量磁系表面不同距离磁场强度得出；R为涡流分选筒直径；k为涡流筒内 N-S 磁极对数，在本模型中k值取 9；ω表示旋转磁辊的角速度，金属导体在磁场中视为磁力线垂直穿越导体，因此ϕ-ωt=π/2。

由于当n=2 时，b2(r/R)-46≈0，故而金属导体有效磁场强度经过计算可以简化为

3 导电体颗粒所受涡流力

金属导电体颗粒经过方向不断变化的磁场时，其内部会产生方向不断改变的涡电流，由于涡电流的方向不断变化，新产生的磁场磁通量φp与磁辊磁场磁通量φm方向相反，相互排斥，两者之间的排斥力被称为涡流力。将铝片颗粒假设为一个磁极，则涡流力可以理解为 2 个方向相反的磁极间的作用力。

式中：l为 2 个磁极之间的距离。

由图 1 可知，2 个磁极之间的径向距离

式中：θ为笛卡尔坐标系中导电体与磁辊中心连线与y轴的夹角。

假设磁辊转动产生的磁场垂直穿越物块的最大截面积SP，磁辊磁场在金属导电体引起的通量

原片形金属导电体内部涡电流形成的磁场磁通量[9]

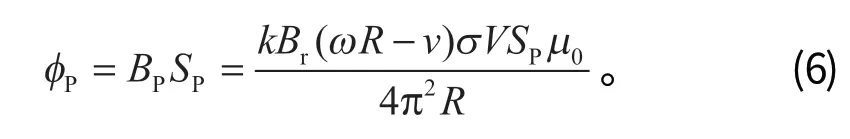
将式 (3)～(5) 代入式 (6) 可得，圆形金属导体片在变化磁场中受到的涡流力

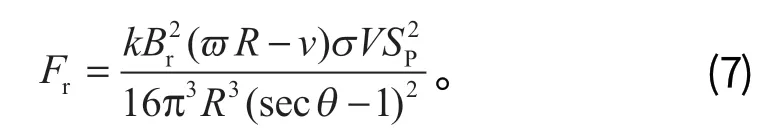
式中：Br为接触点磁场强度，A/m；ϖR-v为导电体和转动磁系的相对速度差，m/s，忽略导电体和传送带之间的滑动，认为物块运动速度和传送带速相等；σ为金属导电率；V为材料体积；SP为垂直磁场方向的横截面积。

由式 (7) 可见，磁场强度、导电体体积、导电体横截面积、磁辊转速、导电体运动速度和电导率等参数，都会影响导电体在分选过程中受到的涡流力。

4 弹射角影响因素

不考虑传送带和金属导体的相对滑动，金属导电体在随传送带运动过程中，当导电体块距离磁辊表面较远时，受到的磁场力较小，导电体处于静止状态，此时最大静摩擦力f0≥μkN(μk为静摩擦因数；N为导电体受到的支撑力)。

当随传送带一起沿磁辊切线方向逐渐靠近磁辊时，磁场强度逐渐增大，受到的电磁斥力逐渐变大。当电磁斥力在y轴上的分力大于导电体自身重力时，即Frcosθ≥G，导体颗粒从磁辊表面脱离，该点与y轴的夹角即为弹射角。弹射角可以定量描述物料分离的难易程度，弹射角越大，越容易分选；弹射角越小，越不容易分选。

4.1 导电体材质及尺寸

在磁辊转速为 2 000 r/min、给料速度为 1 m/s 的条件下，分别绘制φ10 mm 和φ20 mm 且厚度为 1 mm的圆形铜片和铝片各自涡流力变化曲线，并将各自自重力线也画在图中，每个金属片的自重力线与各自涡流力曲线的交点所对应的横坐标值即为该金属片的弹射角。

图4 铜片和铝片涡流力变化曲线Fig.4 Variation curve of eddy current force of copper sheet and aluminum sheet

由图 4 可知，随着导电金属体随着传送带运动逐渐接近旋转磁辊，其所受的涡流力在极短的范围内急剧增大，当涡流力向上分量大于自重力时，导电体被弹射出去。φ10 mm 与φ20 mm 的铜片的弹射角分别为 9.2°和 16.9°，φ10 mm 和φ20 mm 的铝片的弹射角分别为 10.4°和 19.6°。可见同种材质及形状下，随着截面积的增大，弹射角逐渐增大，这表明在合理范围内增大分离物料直径，可降低其分离难度。此外，φ10 mm 铜片和铝片的弹射角差值为 1.2°，弹射点距离较近，而φ20 mm 铜片和铝片的分离角差值为2.7°。因此，为了避免铜铝彼此之间的相互干扰，也应该增大分选物料直径。

虽然铜片电阻率 (1.75×10-8Ωm) 低于铝片电阻率(2.83×10-8Ωm)，但是在相同直径条件下，铜片的弹射角要小于铝片的弹射角，这是由于铜片密度 (8.9×103kg/m) 远大于铝片密度 (2.7×103kg/m)，造成铜片脱离所需要的涡流力也远大于铝片，脱离难度较大，表现为铜片后于铝片脱离传送带且飞跃距离较短。

4.2 磁辊转速

分别计算出φ5、φ10 mm 的圆形铜片及铝片在不同磁系转速下的弹射角，如图 5 所示。

由图 5 可知，随着磁系转速的增大，铜片及铝片的弹射角都会出现不同程度的增大。在转速由 1 500增大到 2 500 r/min 时，弹射角增大较为明显；2 500 r/min 以后，随着转速的增大，弹射角增大幅度逐渐减小。

图5 磁辊转速和弹射角关系曲线Fig.5 Relationship curve of magnetic roll speed and ejection angle

4.3 传送带速度

涡流分选过程中，传送带与磁辊是独立运转的，在磁辊转速为 2 000 r/min，传送带速度为 1 m/s 和 2 m/s 条件下，分别计算出φ20 mm 的圆形铜片和铝片的涡流力变化曲线，如图 6 所示。

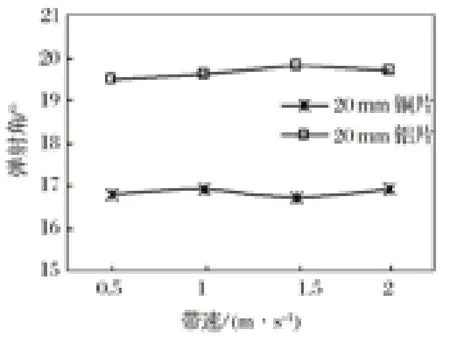
图6 带速和弹射角关系曲线Fig.6 Relationship curve of belt speed and ejection angle

由图 6 可知，相同材料在不同带速条件下，弹射角变化不大。因此，在分选过程中，带速可以根据设备处理能力进行最优选择，但是要注意传送带速度不可过快，否则易造成分离物料颗粒在磁场分离区打滑，进而影响分选效果。

5 结论

(1) 磁辊同一半径磁场强度有高有低，在磁辊转动的过程中，由于磁辊转速较快，低磁场区域会被高磁场区域覆盖，在磁辊表面形成分布近似均匀的等效磁场，通过对磁场的有限元分析，建立磁辊等效磁场数学公式。

(2) 将磁辊磁场和导电体内涡电流形成的感生磁场各作为一个磁极，通过磁极间作用力公式建立圆形导电体涡流力数学模型。

(3) 提出弹射角可作为评估有色金属导电体涡电流分离难易程度的量化指标。在合理范围内增大分离物料直径，弹射角增大，分离难度降低，同时也能增大铜片和铝片弹射角的差值，避免相互干扰。

(4) 对于具有相同外形尺寸的不同导电体，在相同的分离条件下，其分离的难易程度主要由导电率和密度共同决定。

(5) 在合理范围内增大磁辊转速，可增大弹射角；传送带的速度对于弹射角影响不大。