研磨介质形状对球磨机特性影响的DEM 模拟研究

浙江大学能源工程学院化工机械研究所 浙江杭州 310027

在 球磨机的工作过程中，研磨介质对于球磨机工作特性的影响主要表现在研磨介质的形状、大小和填充率等方面。为了提高球磨机的工作效率，选取合适的研磨介质非常重要。目前球形研磨介质和圆柱形研磨介质的应用最为广泛。随着近年来计算机技术的蓬勃发展，在颗粒体系的研究中，离散单元法 (Discrete Element Method，DEM) 逐渐走入人们的视野，该方法在颗粒的混合分离[1]、物料破碎[2]及气固两相流动耦合[3]研究等许多领域得到了应用。Mishra 和Rajamani 首次利用二维 DEM 模型对球磨机内的颗粒运动进行研究[4]；随后，Cleary 也利用该方法研究了球磨机转速对颗粒行为 (如转矩、功率等方面) 的影响[5]。为了使模拟过程更加接近实际情况，Cleary 首次利用三维 DEM 模型[6-7]来预测球磨机的能量损耗，并对于该模型的精确度做出了验证[8]；随后基于该模型，研究人员在填充率、转速和提升条的形状及数量，以及颗粒的材料特性等方面进行了许多研究[9-11]。

由于非球形研磨介质的建模难度较大，过去研究人员多针对球形研磨介质，采用 DEM 模型进行模拟。在球磨机实际操作过程中，非球形研磨介质的应用范围也非常广泛，而目前仍然缺少对非球形研磨介质与球形研磨介质在球磨机内颗粒行为差异的系统性研究。笔者在超椭球模型[12-13]的基础上，建立了 4 种不同形状的颗粒模型 (包括 1 种球形颗粒及 3 种圆柱形颗粒)，首先验证了离散单元法预测球磨机内研磨介质运动的精度，随后对不同形状研磨介质在球磨机内的工作过程进行模拟，对其在功率、运动特性、碰撞能量及磨损等方面的差异进行了比较。

1 研究方法

1.1 研磨介质模型

在三维笛卡尔直角坐标系中，当超椭球中心位于坐标原点、主轴位于坐标轴上时，得到的曲面方程称为超二次曲面方程[14]，其标准公式为

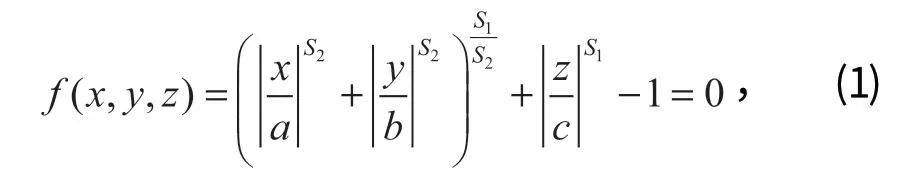
式中：a、b、c为颗粒沿主轴方向的半轴长；s1、s2为形状参数，选取不同的形状参数可以得到不同形状的封闭曲面。

图1 所示为 4 种研磨介质，其相应的尺寸参数如表 1 所列。

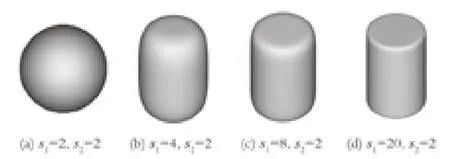
图1 4 种研磨介质Fig.1 Four kinds of grinding media

1.2 研磨介质运动方程

DEM 中的研磨介质运动方程遵循牛顿运动定律，对于球磨机内的单个研磨介质i，其瞬时运动状态由 2 种力决定，分别为接触力和重力。

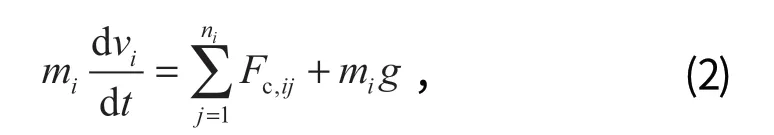
式中：mi为研磨介质的质量；Fc,ij为研磨介质i和j的接触力 (j可以是与i碰撞的研磨介质或衬板)；ni为碰撞次数；g为重力加速度。

研磨介质的旋转由其转矩决定，

式中：Ii为惯性张量；Tc,ij为接触转矩；ωi为角速度。

球形研磨介质由于具有对称性，其惯性张量Ii和接触转矩Tc,ij很容易通过计算得到。然而当非球形研磨介质旋转时，全局坐标系中的惯性张量Ii是随时间变化的，所以非球形研磨介质的惯性张量Ii和接触转矩Tc,ij难以通过同样的计算方法得到。为了解决这个问题，需要一个局部坐标系：首先，在全局坐标系中确定的接触转矩Tc,ij通过旋转矩阵转换成局部坐标系，一旦研磨介质之间发生接触，通过标准的软球线性弹簧-阻尼模型[15]就可以确定研磨介质之间的接触力，然后再通过这些接触参数计算接触转矩；随后，利用转换矩阵将局部坐标系下的旋转运动用全局坐标系来表示，并确定非球形研磨介质在全局坐标系中的位置。众多研究[16-19]已对非球形颗粒在 DEM 框架内的建模进行了描述，在此不再详述。

1.3 接触模型

为了计算研磨介质之间的接触力，采用线性弹簧-阻尼模型[15]。研磨介质i和j之间的法向接触力Fc,n,ij和切向接触力Fc,t,ij分别为

式中：kn、kt分别为法向弹簧刚度和切向弹簧刚度；δn,ij、δt,ij分别为 2 个接触研磨介质间的法向位移和切向位移；ηn、ηt分别为法向阻尼系数和切向阻尼系数；vn,ij、vt,ij分别为研磨介质之间的法向相对速度和切向相对速度。

当 2 个接触的研磨介质 (或研磨介质和衬板) 之间发生滑动，满足以下等式时：

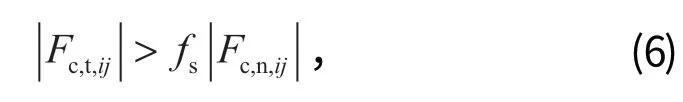
采用库仑摩擦模型来计算切向接触力

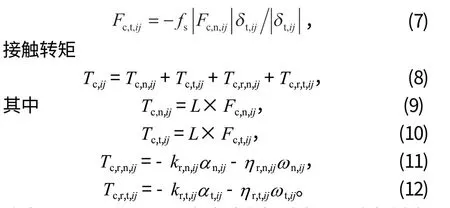
式中：Tc,n,ij、Tc,t,ij分别为由法向接触力和切向接触力引起的转矩；L为从研磨介质中心到接触点的距离矢量；Tc,r,n,ij、Tc,r,t,ij分别为通过滚动产生的法向转矩和切向转矩，滚动轴的方向分别与法向接触力平行和垂直；kr,n,ij、kr,t,ij分别为法向和切向扭转约束刚度；αn,ij、αt,ij分别为 2 个接触研磨介质之间的法向和切向扭转位移；ηr,n,ij、ηr,t,ij分别为法向和切向扭转阻尼系数；ωn,ij、ωt,ij分别为接触磨介在法向和切向上的相对角速度。

当法向转矩和切向转矩满足以下关系时：

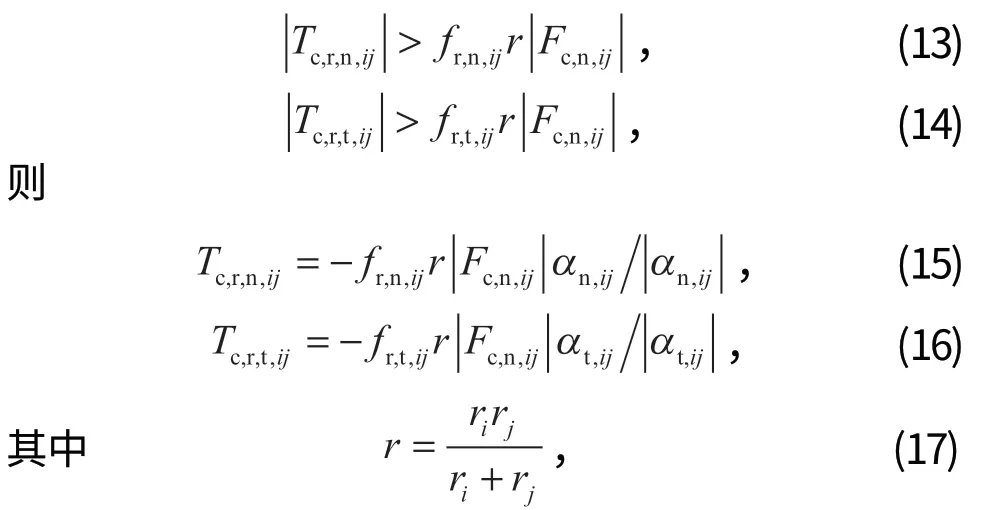
式中：fr,n,ij和fr,t,ij分别为法向和切向滚动摩擦因数；r为研磨介质的有效半径；ri和rj为 2 个接触的研磨介质i和j的等效半径，如果是研磨介质与壁面接触，则有效半径即为研磨介质的半径。

1.4 磨损模型

采用剪切冲击能量模型 (SIEM)[20]计算球磨机衬板的磨损。撞击后衬板表面的损失量

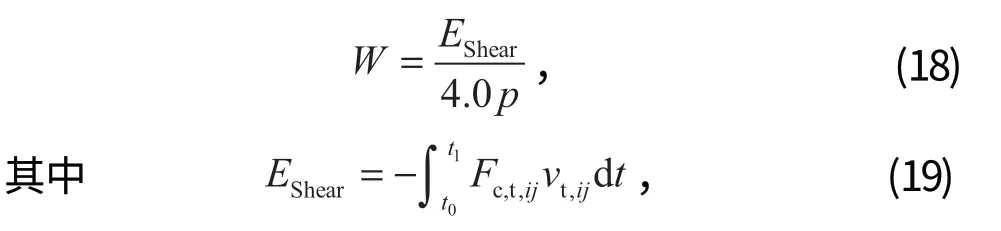
式中：EShear为剪切冲击能量；p为接触面的塑性流动压力，通常是维氏硬度的 1～5 倍；t0、t1分别为研磨介质开始接触的时间和分开的时间。

在冲击期间，累积计算由表面吸收的剪切冲击能量EShear，并在以下两式同时成立时计算磨损：Fc,t,ij vt,ij< 0，Fc,t,ij vij< 0。

根据 Finnie 等人的试验数据[21]，钢材的塑性流动压力设置为维氏硬度的 1.5 倍。关于剪切冲击能量模型 (SIEM) 的更多细节可以参考我们之前的论文[20，22]。

2 模拟参数及计算条件

为了验证 DEM 对球磨机内研磨介质行为预测的准确性，选取 Bian 等人[23]的试验进行模拟验证。试验选取内径为 573 mm、轴向长度为 160 mm 的球磨机，球磨机滚筒内部装有 24 个高度为 10 mm、顶部宽度为18 mm 的提升条。模拟时选取与试验相同的设备。

选用的研磨介质基于超椭球模型构建。如前文所述，当s1=s2=2 且a=b=c时，研磨介质为标准的球体；保持s2=2 不变，增大s1的值，研磨介质的边缘表现得越来越尖锐，且整体形状上越来越趋向于圆柱体。图 1 所示的 4 种研磨介质的s1值分别为 2、4、8 和 20，s2值均为 2。对于s1为 4、8、20 的研磨介质，设定c=1.5a=1.5b，这样可以得到长径比均为1.5 的 3 种近似圆柱体的研磨介质。除此之外，将每种形状的研磨介质分成等效直径分别为 8、13、15 和 20 mm 的 4 组，得到 16 种不同的研磨介质，具体如表 1所列。

在 5 种不同的球磨机转速条件下，对每种研磨介质进行模拟，球磨机转速分别为 33.45、39.02、41.82、44.60 和 50.18 r/min，即球磨机临界转速的60% (球磨机转速与临界转速的百分比用ψ表示)、70%、75%、80%、90%。利用自行开发的 DEM 程序进行模拟，其优势在于可以精确描述非球形颗粒的形状，并在保证模拟精度的前提下，完成对圆柱形研磨介质运动行为的预测。材料参数如表 2 所列。

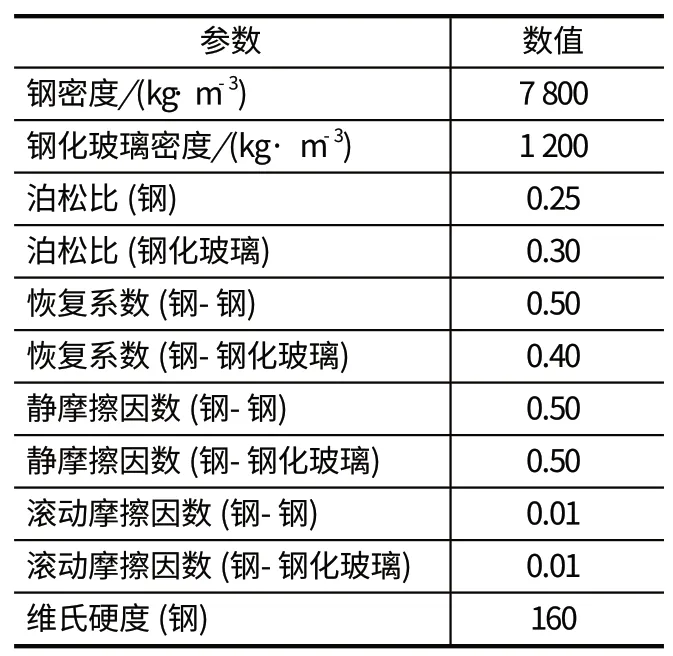
表2 材料参数Tab.2 Parameters of material

3 结果分析

3.1 模型验证

选取 Bian 等人[23]的试验来验证自行开发的球磨机 DEM 模型，试验选取了 4 种不同尺寸的钢球，具体数量及配比如表 3 所列。从 DEM 模拟中可以获取球磨机的功率，并将模拟结果与试验结果做比较，如图 2 所示。由图 2 可以看出，除了球磨机转速为临界转速的 90% 以外，其余 3 种情况的模拟与试验结果基本吻合，因此，可以说笔者选取的模拟方法具有相当高的精度。另外，为了保证模拟精度，在后面的研究中尽量避免球磨机在超过 90% 临界转速条件下工作。

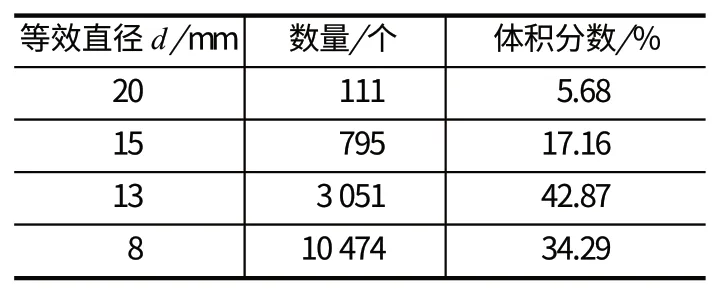
表3 球形研磨介质粒度分布[23]Tab.3 Size distribution of spherical grinding media

3.2 研磨介质的运动特性

为了研究球磨机内球形研磨介质和圆柱形研磨介质的运动特性，采取 Owen 等人[24]所选用的命名法，对 4 种关键位置给出定义，如图 3 所示。

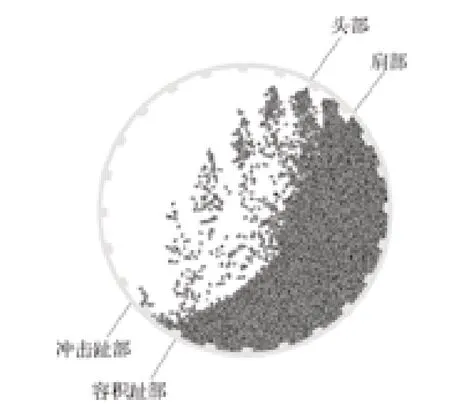
图3 球磨机内研磨介质关键位置的定义Fig.3 Definition of key location of grinding media in ball mill

(1) 头部 研磨介质与衬板接触的最高位置称为头部，该位置是物料流离开衬板的最高点，也就是物料瀑流区域的顶部。

(2) 肩部 连续流动的研磨介质的顶部称为肩部区域，该区域的研磨介质向下流向趾部区域。

(3) 冲击趾部 研磨介质直接撞击衬板的区域最高点称为冲击趾部。

(4) 容积趾部 连续流动的研磨介质的末端区域称为容积趾部，该区域中的磨介运动方向改变并随衬板移动。

选择等效直径为 8 mm 的球形和圆柱形研磨介质进行模拟，从模拟结果得出 3 种圆柱形研磨介质的分布并没有显著差别，因此仅选用一种圆柱形研磨介质(s1=20，s2=2) 与球形研磨介质进行比较。将位置量化为由 12 点钟方向顺时针扫过的角度，可以反映出不同研磨介质在球磨机稳定工况下的分布差异，模拟结果如图 4 所示。显然，球形和圆柱形研磨介质的头部和肩部位置的垂直高度都随着球磨机转速的增加而增加。另外，在相同转速下，圆柱形研磨介质具有比球形研磨介质更高的头部和肩部位置，也就是说圆柱形研磨介质更容易被提升到一个较高位置。就冲击趾部的位置而言，相同转速下圆柱形研磨介质也具有比球形研磨介质更高的垂直高度。另外，2 种研磨介质容积趾部的垂直高度随着球磨机转速的增加而降低，相同转速下，圆柱形研磨介质具有比球形研磨介质更低的容积趾部位置。

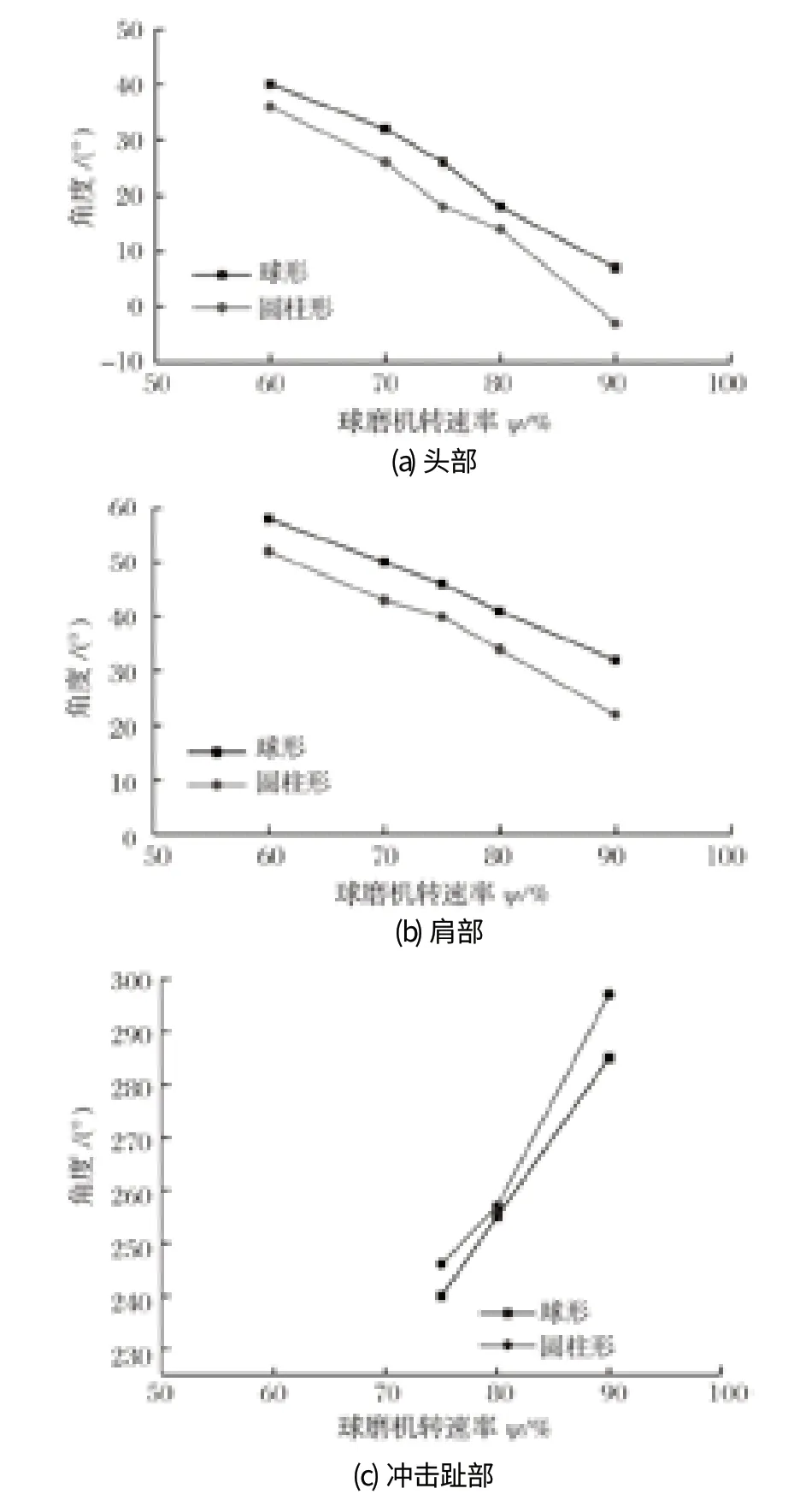
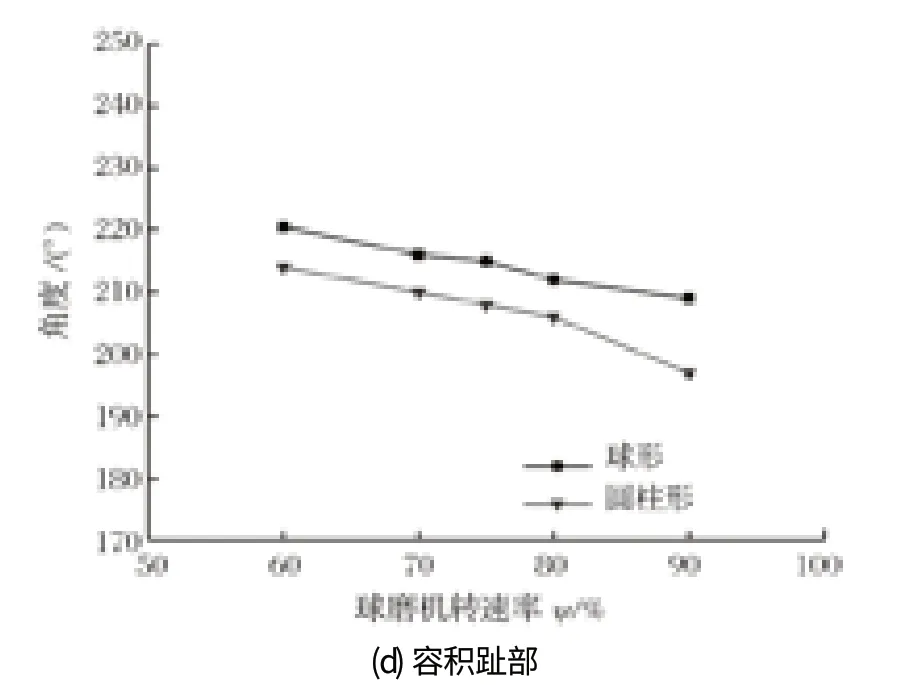
图4 球磨机内球形和圆柱形研磨介质在不同转速下的关键位置角度Fig.4 Angle of key location of spherical and cylindrical grinding media in ball mill at various rotary velocity

当球磨机旋转时，研磨介质从滚筒底部移动到肩部位置，随后开始滑动，在重力作用下在自由表面滑动到趾部位置从而完成循环。根据 Ma 和 Zhao[25]之前的研究，圆柱形颗粒之间的互锁作用对颗粒的运动有着重要的影响。在球磨机中互锁现象依然存在，它限制了堆叠的圆柱形研磨介质彼此之间的滑动。因此相对于球形研磨介质，肩部位置的圆柱形研磨介质更加难以滑动。在容积趾部同样如此，圆柱形研磨介质更难以分散在球磨机的底部，这使得大多数堆叠的圆柱形研磨介质 (即类似于肾脏形状的部位) 的流动间歇性较高。

根据之前的研究结果[24]，球磨机的工作条件 (如转速、填充率和提升条形状等) 对研磨介质运动行为有着显著的影响。在本研究中，由于提升条高度及研磨介质填充率等参数保持恒定，因此研磨介质的运动行为差异主要受球磨机的转速以及研磨介质的形状所影响。为了更直观地观察稳定状态下研磨介质运动状态的差异，截取球磨机在 33.45 (ψ=60%) 和 44.60 r/min (ψ=80%) 2 种转速下的研磨介质的运动瞬态图，如图 5 所示。

从图 5 可以看到，边缘较为光滑的圆柱形研磨介质 (s1=4) 比其他 2 种棱角更加尖锐的圆柱形研磨介质 (s1=8 和s1=20) 更接近于球形研磨介质 (s1=2)，且随着s1的增加，研磨介质在磨机中的分布变得更加密集。如前文所述，在相同的球磨机转速下，圆柱形研磨介质具有较高的肩部和头部位置，以及比球形研磨介质更低的容积趾部位置 (即圆柱形研磨介质的瀑流弹道轨迹更高)。为了探究原因，截取转速为44.60 r/min (ψ=80%) 时球磨机头部位置的球形和圆柱形研磨介质的瞬态图，如图 6 所示。

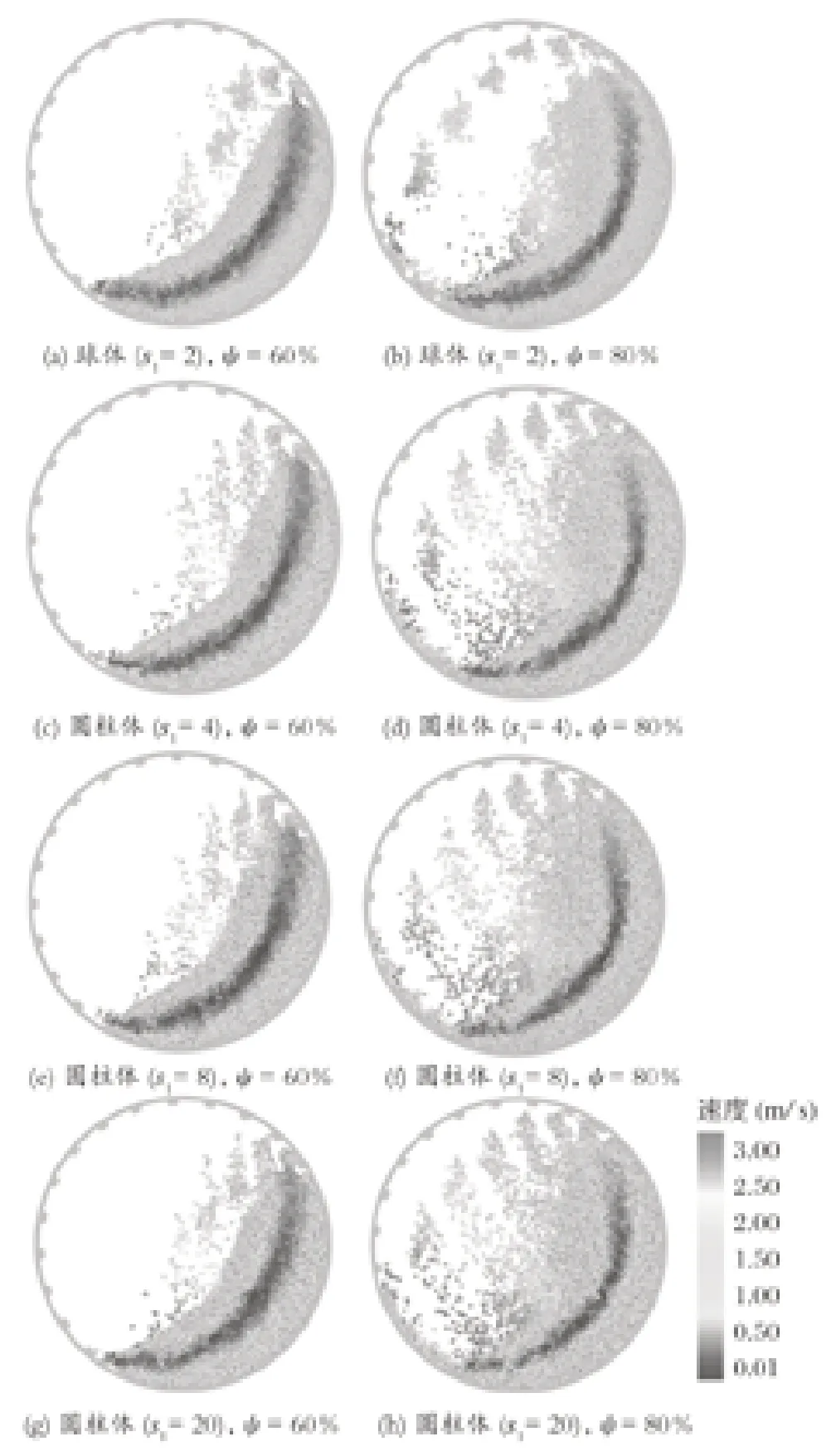
图5 不同转速下研磨介质的运动状态Fig.5 Motion state of grinding media at various rotary velocity

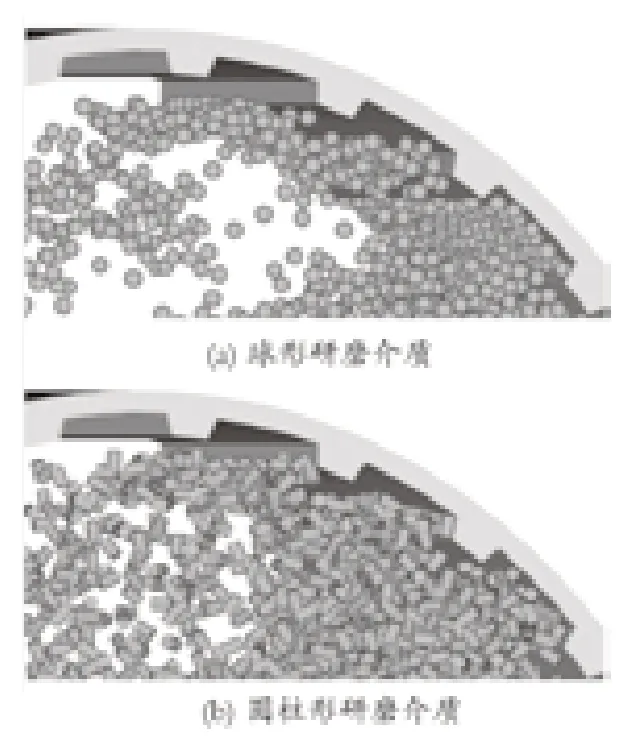
图6 球磨机头部位置的球形和圆柱形研磨介质瞬态图Fig.6 Transient state of spherical and cylindrical grinding media at toe of ball mill

显然，在球磨机顶部的圆柱形研磨介质分布比球形更加密集，这意味着更多的圆柱形介质可以通过提升条提升到球磨机的顶部，并且球形研磨介质相对于圆柱形研磨介质更容易从提升条滑落或滚落。从图 6可以发现，当研磨介质即将离开提升条时，圆柱形研磨介质的母线或两个端面更倾向于紧贴在提升条上，这导致圆柱形研磨介质和提升条之间存在更严重的滑动摩擦，使得圆柱形研磨介质相对于球形研磨介质更难以在低位脱离提升条。因此，提升条会在高位抛出更多的圆柱形研磨介质，这种现象在球磨机转速较高的情况下尤其明显。

3.3 功率损耗

为了研究研磨介质的形状和尺寸对球磨机功率的影响，对上述 4 种等效直径为 8、13、15 和 20 mm 的研磨介质进行模拟。图 7 显示了球磨机不同转速下 4种研磨介质的功率。

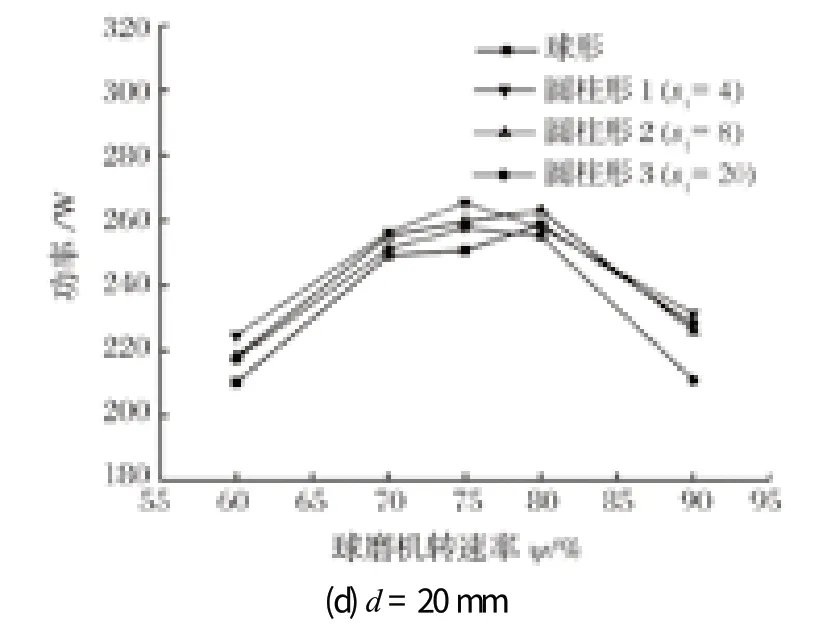
图7 不同转速下 4 种研磨介质的球磨机功率比较Fig.7 Comparison of power of ball mill containing four kinds of grinding media at various rotary velocity

从图 7 可以观察到，球形研磨介质除直径为 20 mm 的情况外，功率通常随着转速的增加而增加，而圆柱形研磨介质的功率在达到峰值后下降。当球磨机的转速低于 44.60 r/min (ψ=80%) 时，圆柱形研磨介质在相同转速下的功率消耗明显高于球形。随着球磨机转速的进一步增加，圆柱形研磨介质的离心运动越来越明显，从而导致功率下降。而当研磨介质的尺寸增加时，这种现象更加明显。如前文所述，这是由于圆柱形研磨介质与提升条之间存在更多的线接触和面接触，从而产生了更大的滑动摩擦力，使得圆柱形研磨介质更容易被提升器提升，所以当球磨机的转速较高时更容易离心，这导致装有圆柱形研磨介质的球磨机的功率低于球形研磨介质。当研磨介质的尺寸增加时，所有研磨介质都更容易离心，因此功耗大大降低。

3.4 碰撞能量

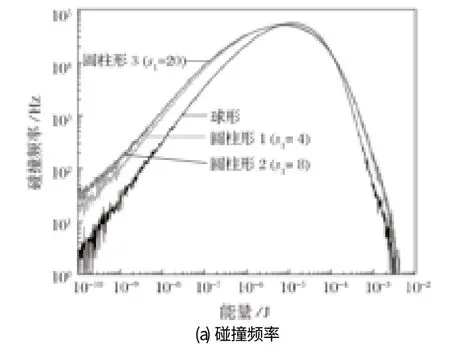
图8 显示了转速为 33.45 r/min (ψ=60%) 时研磨介质之间的碰撞频率和能量耗散率曲线。从图 8 可以明显看出，由于相似的形状，s1=8 和s1=20 这 2 种圆柱形研磨介质的碰撞频率和能量耗散率曲线几乎重合。与这 2 种圆柱形研磨介质相比，在碰撞能量小于6×10-6J 时，球形和另一种圆柱形研磨介质 (s1=4)的碰撞频率和能量耗散率曲线较低，特别是球形研磨介质的曲线明显低于其他形状的介质。随着碰撞能量的增加，在能量介于 6×10-6～2×10-4J 之间时，球形研磨介质的曲线大幅增加，超过了其他 3 条曲线；随着能量进一步增加，碰撞频率和能量耗散率达到最大值后逐渐减小，球形研磨介质的曲线下降得更快，并且明显低于其他研磨介质的曲线。基于以上分析可以得出结论：在较低转速 (ψ=60%) 时，球形研磨介质的碰撞频率和能量耗散率的分布与圆柱形研磨介质相比较窄，碰撞的能量范围更加集中。

在转速为 44.60 r/min (ψ=80%) 时，研磨介质之间的碰撞频率和能量耗散率曲线如图 9 所示。与低转速 (ψ=60%) 情况相比，球形研磨介质的曲线没有明显变化，然而圆柱形研磨介质的碰撞频率和能量耗散率的分布变得更加均匀，最大值明显低于球形研磨介质。其原因可能是圆柱形研磨介质相对于球形被抛在空中的数量较多，使得圆柱体之间的碰撞比球体之间的碰撞更加复杂。

3.5 衬板磨损

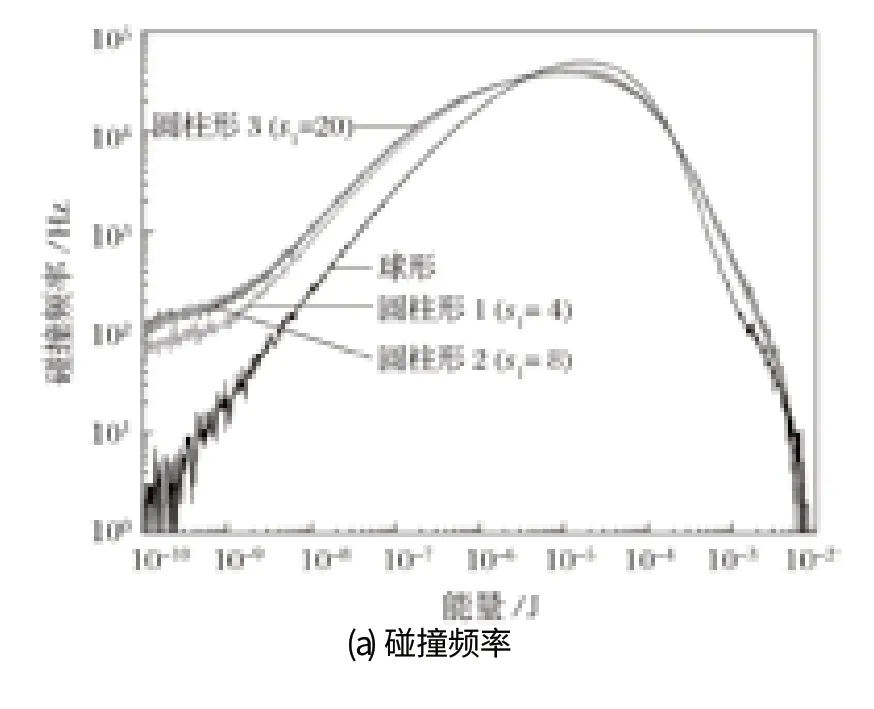
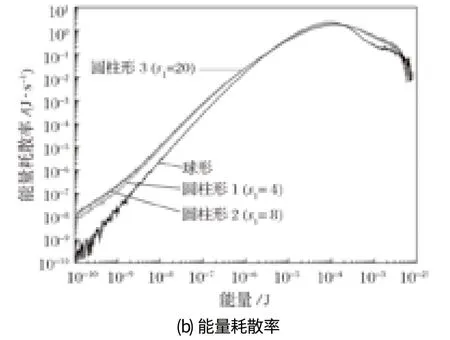
图9 转速为 44.60 r/min (ψ=80%) 时研磨介质间的碰撞频率和能量耗散率曲线Fig.9 Curve of impact frequency and energy dissipation rate of grinding media at rotary velocity being 44.60 r/min (ψ=80%)

衬板磨损问题是球磨机应用中的常见问题。在相同的工作条件下，选择球形和圆柱形研磨介质 (s1=20) 来探索研磨介质形状对衬板磨损的影响。对 2 种研磨介质在球磨机稳定状态下旋转一圈所造成的衬板磨损量进行对比，结果如图 10 所示。显然，研磨介质对衬板的磨损量随着球磨机转速的增加而增加。与球形研磨介质相比，相同转速下圆柱形研磨介质对衬板的磨损更加严重。经分析认为是由于以下两个原因：首先，与同一转速下的球形研磨介质相比，提升条会抛出更多高速运动的圆柱形研磨介质，直接撞击衬板造成极大的磨损，这也解释了转速越高两者差值越大的原因；其次，在圆柱形研磨介质和衬板之间存在更多的滑动，导致更多的滑动摩擦力做功，使得磨损现象更加明显。

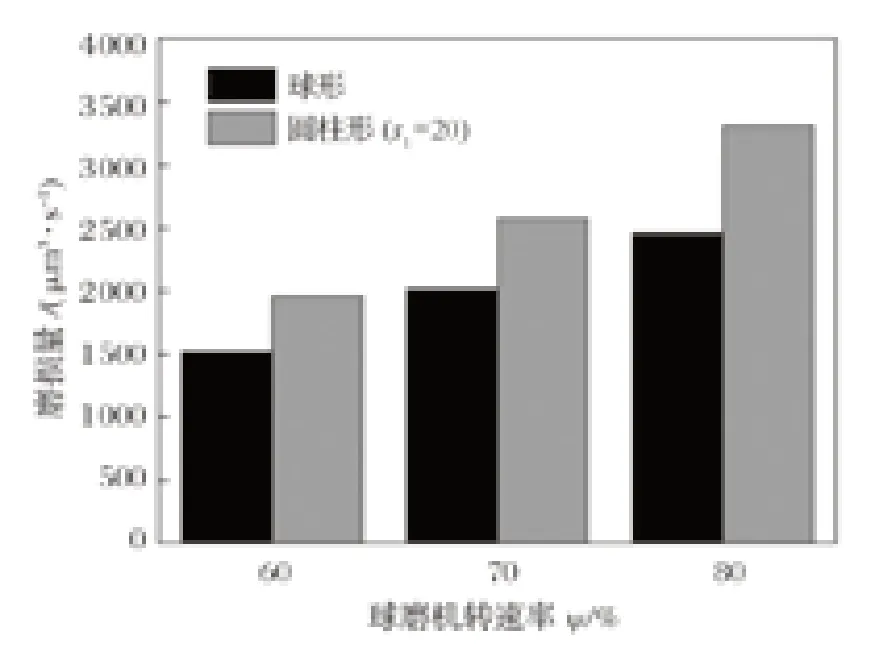
图10 不同转速下 2 种研磨介质对球磨机衬板的磨损量比较Fig.10 Comparison of liner wear amount of ball mill containing two kinds of grinding

4 结论

基于超椭球模型并利用离散单元法研究了 4 种不同形状研磨介质对球磨机内物料运动行为的影响，主要可以得到以下结论：

(1) 在研磨介质运动特性方面，在相同的工作条件下，相对于球形研磨介质，圆柱形研磨介质的头部、肩部以及冲击趾部垂直高度较高，容积趾部高度较低。

(2) 在功率损耗方面，在相同的工作条件下，圆柱形研磨介质的功率一般高于球形研磨介质，但在球磨机高转速条件下，由于圆柱形研磨介质存在更明显的离心运动，会使得功率显著下降。

(3) 在碰撞能量方面，在较低转速 (ψ=60%) 条件下，圆柱形研磨介质之间的碰撞频率和能量耗散率分布得更为均匀，当转速较高 (ψ=80%) 时，这种现象更加明显。

(4) 在设备磨损方面，在相同的工作条件下，圆柱形研磨介质对衬板的磨损大于球形研磨介质。