基于ARIMA模型的国内生产总值预测

蔡淅韵

近年来，中国国内生产总值保持较快增长，经济总量不断扩大，发展取得显著成就。国内生产总值（GDP），是指按照市场价格计算的一个国家或地区所有常住单位在一定时期内生产活动的最终成果，能够反映经济实力和市场规模。如何利用适当的模型对其进行时间序列分析和预测，对更好地研究国家经济表现具有重要的经济意义。为了更好地研究国家的经济表现，本文选取季度GDP作为经济指标，对该指标进行分析，建立了包含趋势和季节成分的ARIMA模型并进行短期的季度预测。

1 基于ARIMA模型的GDP预测理论模型

对GDP进行短期预测时，季节性ARIMA模型能够刻画出数据变化特征和周期性特征。利用ARIMA模型建模首先需要对序列平稳性进行识别。一般来说，经济运行的时间序列都不是平稳序列，则需要对数据进行差分处理。如果数据存在异方差需进行对数运算，直到处理后数据的自相关函数值、偏自相关函数值无显著地异于0。在生活中，部分时间序列具有明显周期性季节效应、趋势效应和随机波动。首先求出季节效应拟合St，并采用中心化的方法将该估计加以修正得到新的估计，最终通过差分处理消除趋势效应的影响。根据时间序列模型的识别规则，建立相关的模型：若平稳序列的偏相关系数是截尾的，而自相关函数是拖尾的，可断定序列适合AR模型；若平稳序列的偏相关系数是拖尾的，而自相关函数是截尾的，则可断定序列适合MA模型；若平稳序列的偏相关系数和自相关函数均是拖尾的，则序列适合ARMA模型。

2 实例分析

本次建模中，所使用数据为1992—2018年的全国GDP季度数据，数据来源于中经网统计数据库。利用1992—2016年共100个季度GDP数据作为训练集设定模型参数，用2017—2018年的数据检验模型的拟合效果及误差分析，比对预测值和实际值以验证模型的可信度，最后预测2019—2021年。

2.1 数据波动性分析

由原序列xt的时序图可以看出该序列有非零均值、有明显的增长趋势，说明该序列是非平稳且存在异方差；具有明显的周期性，周期为4个季度，因此可以确定xt是带有趋势性和季节性的时间序列。自相关系数没有随着延迟期数的增加衰减到0的趋势，因此可以认为是xt非平稳序列。由白噪音检验得知在显著性水平为5%时，序列值之间蕴含相关关系，拒绝原序列xt是白噪音的假设。

接着对xt做对数变换消除异方差性，得到序列yt=ln(xt)，进一步观察yt的时序图发现该序列有明显的增长趋势，自相关系数没有随着延迟期数的增加衰减到0的趋势，因此可以认为是yt非平稳序列。由白噪音检验得知在显著性水平为5%时，P值均小于0.05，拒绝yt是白噪音的原假设，即yt不是白噪音，具有研究价值。

2.2 参数估计

自相关函数图显示Zt一阶截尾性质明显，通过BIC信息可判断选用AR(4)模型。在Dickey-Fuller单位根检验中（表1），统计量的P值都明显小于显著性水平5%，可以进行接下来的参数分析。初次参数估计结果显示截距项不显著，去除后重新拟合的结果如表2。可知，在显著性水平5%所有参数的P值都小于0.05，参数显著不为零，因此通过显著性检验。白噪音检验结果表明检验P值均远大于0.05显著性水平，接受序列为白噪音的原假设，可以认为残差序列是白噪音，所以模型显著。

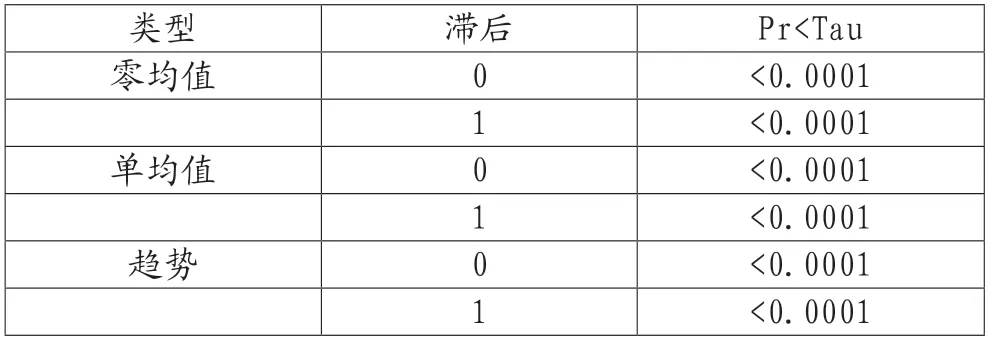
表1 Dickey-Fuller单位根检验

表2 最小二乘法拟合结果

该序列模型为：

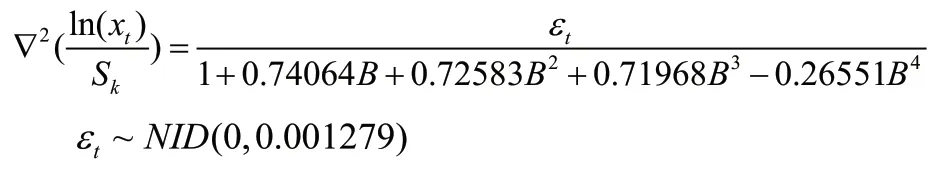
2.3 预测结果

根据拟合模型对2017—2018年的GDP季度数据进行预测，2017年第一季度预测值与实际值相对误差率17.8%，第二季度相对误差率4.3%，第三季度相对误差率12.2%，第四季度相对误差率12.3%；2018年第一季度相对误差率21.7%，第二季度相对误差率0.6%，第三季度相对误差率19.7%，第四季度相对误差率22%。估计标准误差为0.036，AIC值为-370.795。2017年GDP拟合结果平均绝对百分比误差(MAPE)为4.31%；2017—2018年GDP拟合结果平均绝对百分比误差为7.33%；2018年GDP拟合结果平均绝对百分比误差为10.36%。当MAPE值低于10%，则认为预测精度很高，属于高精度预测类型，所以本模型拟合效果较好。可以看出预测值和实际值在4个季度内预测比较准确，随着时间预测的延长，8个季度以上预测误差相对增大。根据2017年及2018年观测的实际值进一步修正模型后，得到2019—2021年12个季度GDP预测值见表3，预测走势见图2。从预测结果上看，国内生产总值仍然延续以往的增长规律，每年的第四季度都是一年中的最大值，这和往年的变化规律是一致的。

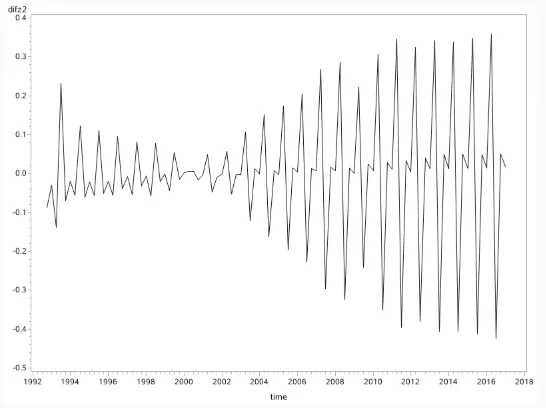
图1 Zt 二阶差分后时序图

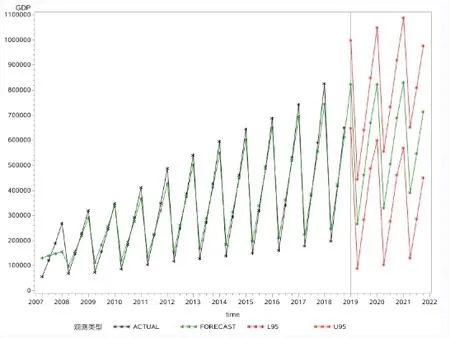
图2 2019—2021年GDP预测走势图

表3 2019—2021年GDP预测值（亿元）

3 结语

针对GDP进行短期预测，首先结合时间序列模型分析GDP数据特征，由于序列非平稳进行差分作平稳化处理，构建季节性ARIMA模型。以2017—2018年数据进行模型参数估计后的测试组，将预测的GDP数据与实际数据进行对比。结果显示，季节性ARIMA模型作为GDP预测模型是可行的，拟合平均绝对百分比误差MAPE等于7.33%，验证了模型有良好的精度。随着时间跨度的增加，该模型的预测值与真实值之间的误差率逐渐增大。但尽管如此，如果在建立模型过程中根据观测的实际值进一步修正模型对8个季度以后的预测，则可以得到精确度更高的预测值。因此从短期来看，ARIMA模型对GDP的预测具有一定的可信度，有一定的实用性。