基于函数型数据的气温与空气质量的相关性分析

杨荣　戴家佳

摘 要：随着我国经济的快速发展，大气污染问题日益严重，旅游城市的空气质量问题也备受关注。本文基于2018年30座热门旅游城市的气温和空气质量数据，从气象条件的角度出发，研究了气温与空气质量之间的关系。采用函数型数据描述性分析的方法对空气质量和气温变化特征进行分析，用函数型回归分析研究气温对空气质量的影响。结果显示：

函数型线性模型拟合优度R2=0.898 1，F=11.821 2大于临界值2.385 9，函数型检验统计量F～=8.723 3大于α=005水平下的临界值1.705 8，说明气温与空气质量的函数型线性关系显著;气温对空气质量呈谐波正负影响交替出现，这与空气质量平均变化相似，在实际生活中是合理的。

关键词：函数型回归模型;基函数;最小二乘估计;气象因素;空气质量

中图分类号：X51;P423

文献标识码： A

2018年聯合国气候大会指出：“要将全球升温控制在1.5 ℃内，如果能够坚持1.5 ℃而不是2 ℃的升温控制，受气候变化影响的人会减少4.2亿”。气候变化和经济社会发展带来的空气质量的恶化对人类健康和生活造成了一定影响。根据环境保护部发布的《环境空气质量指数（AQI） 技术规定（试行）》[1]，参与评价空气质量指数的污染物主要有细颗粒物（PM2.5）、 可吸入颗粒物（PM10）、二氧化硫（SO2）、二氧化氮（NO2）、臭氧（O3）、 一氧化碳（CO）六项。

除了已纳入评价空气质量的这些污染物，气象因素也是影响空气质量水平的因素之一。2013年陈松等[2]研究了驻马店城市温度变化与空气质量的关系;2018年李育慧等[3]指出，在污染源排放相对稳定的情况下，对空气质量水平起主要作用的是气象因素;2018年吕爱丽等[4]研究了大气污染与气象条件的相关性，研究表明PM2.5、PM10、SO2、NO2 浓度与气压存在正相关关系，与温度、降水、风速、日照存在负相关关系;2018年盛永财等[5]应用主成分分析法研究了气象因素对乌鲁木齐市城区空气质量的影响;2018年何佳璐等[6]通过相关分析方法研究了舟山市PM2.5浓度与气象因素的关系，结果表明大气PM2.5浓度随气温上升呈下降趋势，并且与相对湿度、降水量和风速等气象因素呈负相关关系;2018年付伟等[7]研究了芜湖市气象因素对空气质量的影响，结果显示，芜湖市6种污染物表现出不同的季节特征，主要的污染物PM2.5冬季浓度最高，春、夏次之，秋季最低。由此可知气象因素会影响空气质量水平，我们研究气温对空气质量的影响是具有实际意义的。

1991年RAMSAY和DALZELL[8-9]正式提出了函数型数据分析（Functional Data Analysis，FDA），1997年RAMSAY[10]对一些传统统计分析方法进行改进使之适用于函数型数据分析，如主成分分析，线性回归分析和典型判别分析等，总结了函数型数据分析的理论和方法，全面地阐述了函数型数据的特点及其统计分析思想方法，极大地推动了函数型数据分析的发展。在函数型数据分析中，函数型回归模型是一个重要的数据分析工具，它主要用于分析函数型数据协变量与响应变量之间的关系。1999年CARDOT 等[11]使用光滑样条技术和函数型主成分（FPCA）得到了斜率函数的估计，

并研究了估计的渐近性质;2006年CAI和HALL[12]用函数型主成分估计研究了函数型线性模型的估计与预测问题;2010年HALL和YANG[13]分别用样条、主成分估计、偏最小二乘估计研究了函数型线性模型的估计与预测问题。在以往空气质量的研究中，一般采用传统的统计方法对空气质量的影响因素进行分析，但从时间尺度上来看，发现研究空气质量的影响因素的数据具有明显的函数特性，所以本文采用函数型数据分析（FDA）的方法来分析气温与空气质量的关系。函数型数据分析相对于传统的统计分析方法，它依赖的假设条件更少，将数据看为一个动态变化的过程，能挖掘出丰富的数据信息，给出更合理的解释。

本文首先对函数型数据回归模型的基本理论进行介绍，其次利用函数型回归分析讨论2018年30座热门旅游城市空气质量与气温变化之间的关系，并得出相应结论。

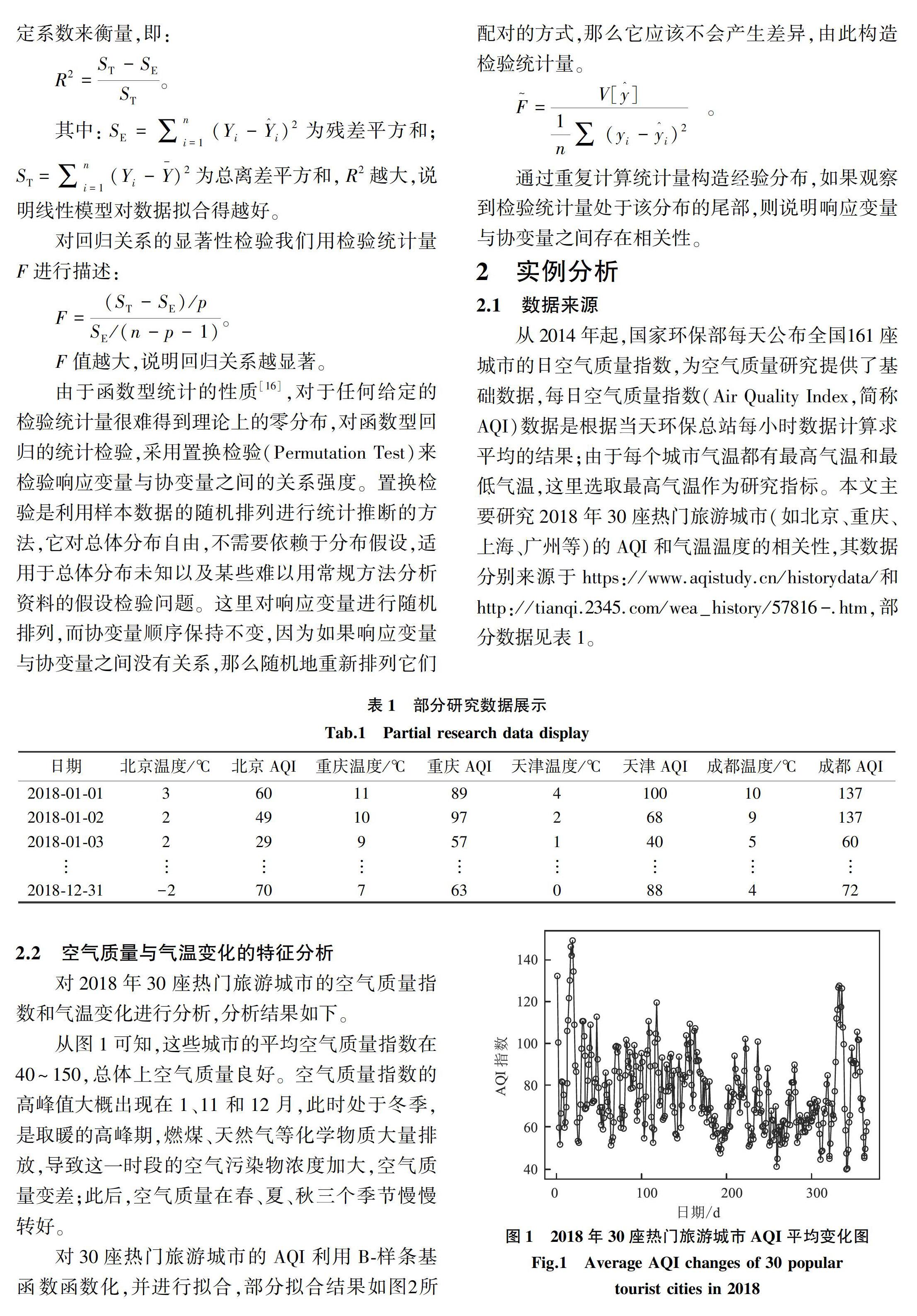
3 结论

本文通过对2018年30座热门旅游城市的气温和空气质量变化特征进行分析，发现这些城市的空气质量变化具有季节性和地域性特征，冬季最差，春秋次之，夏季最好;空气质量由华北向西南地区逐渐变好，并且气温对空气质量有显著性影响。

通过利用函数型回归分析的方法对气温与空气质量之间的响应关系进行探讨，发现气温对空气质量具有显著性影响。经回归诊断，R2=0.933 8，F=11.284 7大于临界值2.521 5，函数型回归诊断的F～=14.084 55大于α=0.05水平下的临界值2.927 7，充分说明了气温与空气质量的函数型线性关系是显著的。根据斜率函数β（t）的估计曲线，发现气温对空气质量是呈正负交替影响的，并且β（t） 的振幅变化越强，气温对空气质量的影响越大。由此，气温不仅可以作为人们出行的晴雨表，也可以作为判断空气质量好坏的晴雨表。

参考文献：

[1]

环境空气质量指数（AQI）技术规定（试行）[J].中国环境管理干部学报，2012，22（1）：44.

[2]陈松，张俊波，房稳静. 驻马店城市温度变化与空气质量的关系分析[J].河南科学，2013，31（6）：855-859.

[3]李育慧，张家斌，李育乔. 漳州市大气颗粒物时空分布特征及其与气象条件的关系[C]//第35届中国气象学会年会 S12 大气成分与天气、气候变化与环境影响暨环境气象预报及影响评估. 合肥：中国气象学会，2018：305-311.

[4]吕爱丽，王会荣，赵晓丽. 临汾市大气污染变化特征及其与气象条件的相关分析[C]//第35届中国气象学会年会 S12 大气成分与天气、气候变化与环境影响暨环境气象预报及影响评估. 合肥：中国气象学会，2018：390-396.

[5]盛永财，孜比布拉·司马义，李颖. 气象因素对乌鲁木齐市城区空气质量的影响[J].环境工程，2018，36（5）：78-83.

[6]何佳璐，李鹏，张永利，等. 舟山市PM2.5浓度与气象因素的關系研究[J].预防医学，2018，30（12）：1245-1247.

[7]付伟，司红君，卢尧，等. 芜湖市空气质量特征及其受气象要素的影响分析[C]//第35 届中国气象学会年会 S12 大气成分与天气、气候变化与环境影响暨环境气象预报及影响评估. 合肥：中国气象学会，2018：128-129.

[8]RAMSAY J O. When the data are functions[J]. Psychometrika， 1982， 47（4）：379-396.

[9]RAMSAY J O， DALZELL C J. Some tools for functional data analysis[J]. Journal of the Royal Statistical Society， 1991， 53（3）：539-572.

[10]RAMSAY J O， SILVERMAN B W. Functional data analysis[M]. New York： Springer， 2005.

[11]CARDOT H， FERRATY F， SARDA P. Functional linear model[J]. Statistics & Probability Letters， 1999， 45（1）：11-22.

[12]CAI T T， HALL P. Prediction in functional linear regression[J]. Annals of Statistics， 2006， 34（5）：2159-2179.

[13]HALL P， YANG Y J. Ordering and selecting components in multivariate or functional data linear prediction[J]. Journal of the Royal Statistical Society， 2010， 72（1）：93-110.

[14]丁辉，许文超，朱汉兵，等. 函数型数据回归分析综述[J]. 应用概率统计，2018，34（6）：630-654.

[15]梅长林，王宁. 近代回归分析方法[M]. 北京：科学出版社， 2012.

[16]RAMSAY J， HOOKER G， GRAVES S. Functional data analysis with r and MATLAB[M]. New York：  Springer， 2009.

（责任编辑：于慧梅）