基于深度学习的多用户Massive MIMO预编码方法

张智强

【摘  要】在下行链路传输场景中，发射机处的功率分配和波束赋形设计至关重要。考虑一个多用户Massive MIMO系统中总功率约束下最大化加权和速率问题，经典的WMMSE算法可以获取次优解，但计算复杂度过高。为了降低计算复杂度，提出了一种基于深度学习的快速波束赋形设计方法，该方法可以离线训练深度神经网络，利用训练后的神经网络求解最优波束赋形解，只需要简单的线性和非线性操作即可完成。实验结果显示，该方法可以逼近WMMSE算法精度的90%以上，同时计算复杂度和时延也大大降低。

【关键词】Massive MIMO;预编码;WMMSE;深度学习

In a downlink transmission scenario， the design of power allocation and beam assignment at the transmitter is critical. This paper considers a problem of maximizing the weighting rate under the total power constraint in a multi-user massive MIMO system， where the classical weighted minimum mean square error （WMMSE） algorithm can obtain suboptimal solutions with high computational complexity. In order to reduce the computational complexity， this paper proposes a fast beamforming design method based on deep learning， which can train a deep neural network offline and use the trained neural network to solve the optimal beamforming with simple linear and nonlinear operations. Experimental results show that the method can approximate more than 90% accuracy of the WMMSE algorithm， while the computational complexity and delay are greatly reduced.

Massive MIMO; precoding; WMMSE; deep learning

0   引言

Massive MIMO是第五代移动通信（5G）的核心技术之一，在提高系统容量和频谱利用率方面起着至关重要的作用[1-2]。在Massive MIMO系统中，设计实时性强、效率高的资源分配算法是一个非常重要的研究方向，特别是在下行传输链路的预编码问题中。传统的基于优化和迭代的预编码算法收敛速度较慢，计算复杂度高[3]，无法满足5G及以上系统实时应用的需求，如自动驾驶车辆和关键任务通信等。即使在毫秒级变化的小范围衰落非实时应用程序中，迭代过程引入的延迟也会使波束赋形解决方案难以满足通信需求。

近年来深度學习（DL， Deep Learning）在无线通信领域的广泛应用，使得在实时学习最优波束赋行时同时考虑性能和计算延迟成为可能[4-5]。国内外学者在这方面都做出了很多研究，文献[6]基于WMMSE算法提出了一种无监督学习的MIMO快速波速赋形方法，该方法相比WMMSE（Weighted Minimum Mean Squared Error，最小化加权均方误差）算法计算复杂度有所降低，并且训练好的神经网络性能接近WMMSE算法性能。但是由于采用无监督学习的方案，网络训练的难度较大。文献[7]提出一种通用的DL框架，并且创造性地使用了监督学习与非监督学习相结合的混合学习方法来提高学习性能并且同时加快收敛速度，在实验结果上不仅实现了近似最优的波束赋形矩阵，而且与迭代方法相比，计算复杂度也大大降低。遗憾的是该文献针对的是MISO信道，没有扩展到更复杂的MIMO信道中。文献[8]提出的基于神经网络的鲁棒分散联合预编码方法，针对MIMO系统的波束赋形，并且增加了算法的鲁棒性，根据CSI的估计值并利用DNN进行分布式预编码，但是该方法需要训练多个学习器，并且也只能达到ZF（Zero-Forcing）算法的性能。

综合上述问题，基于经典的WMMSE波束赋形方案[9]，本文应用深度学习技术到Massive MIMO系统波速赋形设计中，采用监督学习的方案，并且尝试不同的网络的结构，通过优化设计网络的输入输出结构，从而降低神经网络的输出维度，减小模型的训练难度。仿真结果显示，本文提出的方法可以达到WMMSE算法性能的92%以上，并且所采用的MLP网络和CNN网络结构简单，非常容易训练。

1   问题描述和系统模型

如图1所示，考虑一个单小区多用户的Massive MIMO系统，其中基站配备有NT根发射天线，每个小区有K个用户，每个用户配有NR根接收天线。Sk表示用户k的符号向量，表示用户k的预编码矩阵。基站发出的信号可以表示为：

其中矩阵表示从基站到用户k之间的信道矩阵，表示分布为的高斯加性白噪声。假设不同用户的符号向量彼此独立，所有符号向量和噪声也独立。在本问题中，将多用户干扰作为噪声处理，接收端采用线性接收波束赋形。

我们感兴趣的一个基本问题是找到预编码矩阵{Vk}，能够使得系统的加权和速率在基站总功率约束下最大化，其中总功率约束是由基站发射功率限制。数学上，可以写成如下问题：

2   神经网络的输入输出设计

在多用户Massive MIMO系统中，发射天线的数目NT比较大，且通常情况下发射天线数远远大于用户数（NT>>NR），由公式（6）不难看出，预编码矩阵Vk的维度与NT直接相关[10]，如果直接使用信道矩阵H作为系统的输入，将预编码矩阵Vk作为系统的输出，则神经网络的输出维度将变得很高，导致网络的训练变得非常困难。在WMMSE算法迭代的过程中发现，Vk由{Uk ，Wk}唯一决定，而{Uk ，Wk}的维度与发射天线的数目NT无关，所以，考虑使用{Uk ，Wk}作为神经网络的输出，从而大大降低了网络输出的维度。

3   低复杂度预编码学习模型

为降低传统优化迭代算法进行预编码的复杂度，尝试了基于深度学习的预编码方法，采用监督学习的方法进行网络训练[11]。监督学习是训练波束赋形神经网络最直接的方法。在监督学习中采用较简单的神经网络模型（MLP和CNN）。训练样本通过WMMSE算法直接产生。

对于MLP网络来说，由于网络的输入H是一个高维的复数矩阵，考虑把高维矩阵拉伸成一维的张量来处理，考虑到原输入是一个复数矩阵，同时也把复数的实部和虚部也拼接成一维张量。在MLP网络中选择Adam和MSE分别作为优化器和损失函数。网络模型示意图如图2所示：

同样地，对于CNN网络来说，也采取类似的操作，把复数矩阵扩张成一个张量，类似于一张RGB图像，但是在这里只有两个通道，一个代表实部，另一个代表虚部。但是，与传统的具有卷积和池化层的图像处理不同，不会使用池化层，因为它可能会导致信息丢失，从而影响学习效果。在CNN网络中同样选择Adam和MSE分别作为优化器和损失函数。网络模型如图3所示：

4   仿真结果与实验分析

所采用的深度学习框架是Keras，基于python3.60，服务器系统为ubuntu16.04。硬件平台是所在实验室的服务器，配备了两颗Intel Xeon Gold 6148处理器，384 G内存，四块NVIDIA Geforce RTX2080Ti显卡。在训练过程步长设置为0.001，batch_size=512，将整个数据集迭代了500轮。

4.1  实验数据产生

信道矩阵H是由大尺度衰落和小尺度衰落组成，大尺度衰落中的路径损耗参照公式：128+37.6lg（ω）[dB]，其中ω是用户和基站之间的距离（范围在0.1～0.3 km）。噪声功率对每个用户均相同，可以由计算得到，在此信噪比SNR设置为20 dB，假定每个用户的优先级和发送的流数均相同，即αk=1且dk =NR =2。

训练样本集由MATLAB产生，基于经典的WMMSE算法，一共包含50 000条样本数据，其中训练集45 000条，测试集5 000条。在监督学习仿真实验主要基于表2的测试场景：

在图4和图5中，可以看到，在神经网络输入为H，输出为V时，算法的预测精度可以达到文献[9]中WMMSE算法的90%以上，且在三种不同的测试场景下，随着用户数和天线数的增多，性能只是略有下降。把神经网络的输出改为U、W，由于神经网络的输出维度大大降低，网络更易训练，最终得到的神经网络预测精度比输出为V时有明显提升。同时在两图中也可以看出，CNN网络，比简单的MLP网络把信道矩阵实虚部分开张成一维矩阵的预测性能更好一些。

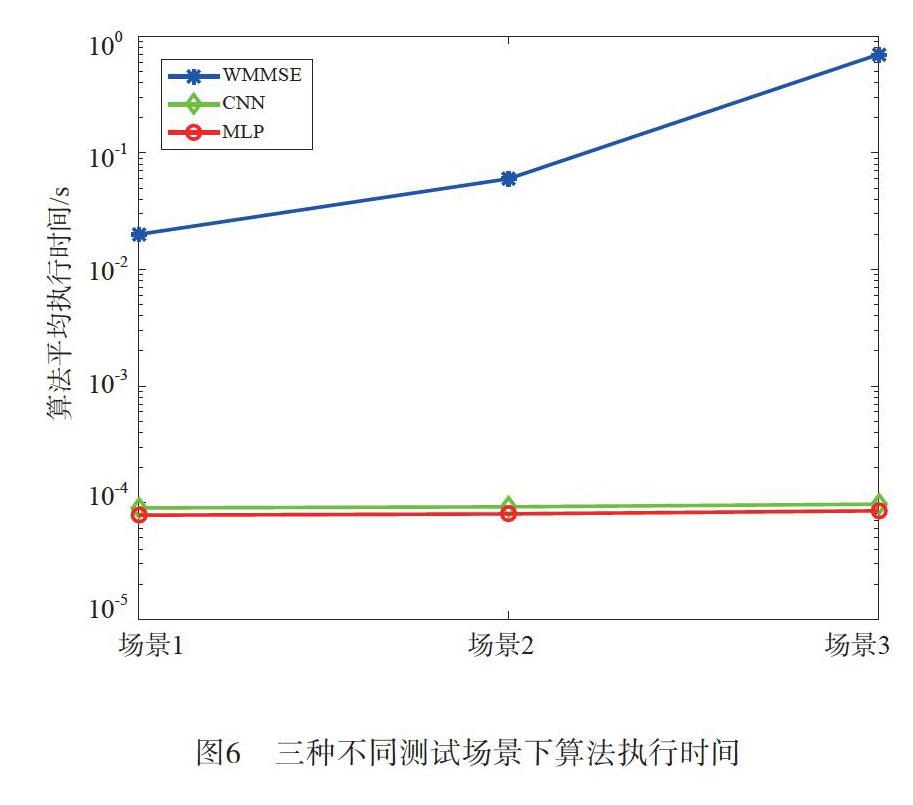
从图6可以看出，在三种不同的测试场景下，MLP网络和CNN网络比传统的WMMSE算法所需更少的算法执行时间。而且，随着基站天线数NT和用户数K的增加，MLP网络和CNN网络所消耗的时间变化不大，但是WMMSE算法的计算复杂度与NT的三次方成正比，故其所消耗的時间大大增加。

5   结束语

为了解决多用户Massive MIMO系统中传统基于优化和迭代的预编码方法收敛速度慢、计算复杂度高的问题，结合当下比较热门的深度学习技术，提出了一种利用神经网络快速逼近经典的WMMSE算法的方法，并且经过重新设计网络的输入输出结构，大大降低了神经网络训练的难度。经过多种网络结构的不断尝试，最终的网络模型不仅可以达到经典的WMMSE算法精度的90%以上，而且在速度和计算复杂度上也大大优于传统的WMMSE算法。在后面的研究中，可以尝试复数域的神经网络模型，另外，除了黑盒神经网络模型，也可以考虑基于WMMSE算法结构构建白盒神经网络，以进一步提高模型的预测精度。

参考文献：

[1]    T L Marzetta， E G Larsson， Y Hong， et al. Fundamentals of massive MIMO[C]//IEEE International Workshop on Signal Processing Advances in Wireless Communications. IEEE， 2016.

[2]    尤肖虎，潘志文，高西奇，等. 5G移动通信发展趋势与若干关键技术[J]. 中国科学：信息科学， 2014，44（5）： 551-563.

[3]   刘斌，任欢，李立欣. 基于机器学习的毫米波大规模MIMO混合预编码技术[J]. 移动通信， 2019，43（8）： 8-13.

[4]   李国权，杨鹏，林金朝，等. 基于深度学习的MIMO系统联合优化[J]. 重庆邮电大学学报：自然科学版， 2019，31（3）： 293-298.

[5]   E G Larsson， O Edfors， F Tufvesson， et al. Massive MIMO for next generation wireless systems[J]. IEEE communications magazine， 2014，52（2）： 186-195.

[6]     H H， W C， J X， et al. Unsupervised Learning-Based Fast Beamforming Design for Downlink MIMO[J]. IEEE Access， 2018.

[7]    X W， Z G， Z Y， et al. A Deep Learning Framework for Optimization of MISO Downlink Beamforming[J]. IEEE Transactions on Communications， 2019.

[8]    P D Kerret， D Gesbert. Robust Decentralized Joint Precoding using Team Deep Neural Network[C]//2018 15th International Symposium on Wireless Communication Systems （ISWCS）. 2018.

[9]    Q Shi， M Razaviyayn， Z Luo， et al. An iteratively weighted MMSE approach to distributed sum-utility maximization for a MIMO interfering broadcast channel[J]. IEEE Trans. Signal Process， 2011，59（9）： 4331–4340.

[10]  S， H， C， et al. Learning to Optimize： Training Deep Neural Networks for Interference Management[J]. IEEE Transactions on Signal Processing： A publication of the IEEE Signal Processing Society， 2018.

[11]  W M A， B F A， A S， et al. Supervised Deep Learning in Fingerprint Recognition[M]. Advances in Deep Learning， 2020. ★