基于改进的Bellman-Ford算法优化中药配送路径

曹 岩，马 健

(亳州职业技术学院 信息工程系,安徽 亳州 236800)

0 前 言

近年来，人们对中药的需求不断增加。公立医院、民企医疗机构和连锁药店的规模不断扩大。亳州作为中国四大药都之一，具有深远的中药材文化和中医文化，中药饮片企业和中药生产企业已超过100家。中药作为一种特殊的商品，与人的生活密切相关，它的使用应严格按照医生的建议，有时微小的错误都将不可避免地影响到人的健康，甚至会影响到生命安全。由于药物本身的特殊性使药品流通过程变得复杂，容易导致资源的浪费和一些不良的社会影响。在保障中药的质量和供应及减少医疗机构的中药的库存积压,中药配送起到了至关重要的作用[1]。利用Bellman-Ford算法分析亳州地区中药配送路径，可以解决中药配送的时间和减少配送的成本，提高中药送达到医疗机构的效率，从而促进社会的发展。

1 亳州地区中药配送问题

在国家政策方针的指导下，亳州市3县1区大力建设各级各类医院和社区卫生服务机构。目前，亳州市共有各级各类医疗机构1 510家，包括医院46家、卫生院94家、社区卫生服务中心(站)98家、村卫生室1 267家、妇幼保健院(所)5家。其中，中心城区共有各级各类医院20家，社区卫生服务中心3家。这些与快速增长的人口数量、日益增长的群众需求相比，仍然存在一定差距。所以，亳州市卫计委在2020-2030年规划中会继续增加医疗机构。

基层医疗机构存在“小、散、多”的现象，对中药的需求量也较少[2]。中药配送企业要按时完成中药配送任务，同时要考虑到中药配送的成本，要合理规划配送路径，提高企业的利润。针对亳州3县1区的医疗机构分布情况和中药需求情况，利用改进的Bellman-Ford算法计算中药配送最优路径，完成企业对中药的配送任务。

2 Bellman-Ford算法分析

Bellman-Ford算法是对所有的边进行V轮降距操作，不再对所有节点划分为2个集合S和V-S。该算法由美国数学家查德·贝尔曼和小莱斯特·福特发明[3]。

对于1个有向图G(V，E),是由从1，2，…，n个点、m条表组成，其中设定1位起始点，w(i,j)位有向边(i,j)的权，dk(i)为点i在第k次迭代后i点的距离标号，那么Bellman-Ford算法步骤如下。

步骤1：将Ak作为k-1轮迭代中距离标号减少的点的集合。

步骤2：初始化，将d0(1)=0,d0(i)=+∞, (2≤i≤n)， 将所有点存放到集合Ak中。

步骤3：对于任意点i(1≤i≤n)， 令dk(i)=dk-1(i)。

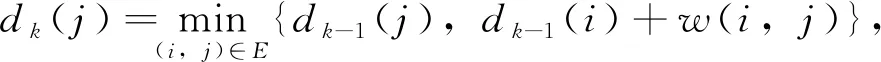
步骤5：执行到集合Ak+1=∅，则算法终止，那么d(i)就是最短距离；如果Ak+1≠∅时，并且k=n-1时，可以得知负循环，算法终止；如果Ak+1≠∅时，k

步骤6：将k=k+1，转到步骤2，继续执行。

算法的伪代码如下：

Bellman-Ford-SHORTEST-PATHS-II(G,S)

(1)d[s] ←0

Statistical downscaling forecast and reconstruction of spatial and temporal correlation of the precipitation

(2)for v∈V-{s} do d[v] ←∞

(3)for i←1 to V-1 do

(4) for edge(u，v)∈E do

(5) if d[v]> d[u]+w(u，v)then d[v]←d[u] +w(u，v)

算法的第1行将源点的距离设置为0，第2行将其他所有节点到源点的距离设置为无穷。从第3行开始，对图中所有的边进行V轮降距操作[4]。第4行的内循环依次对每条边进行考察，并根据情况进行降距操作。第5行为实际的降距操作。

3 改进的Bellman-Ford算法

Bellman-Ford算法在计算最短路径优化过程中具有很好的效率，但还存在不足，在计算距离数目上最多有n2个，而且还增加了算法的存储空间[5]。本文提出了对Bellman-Ford算法的改进，能有效地解决此问题[6]。改进的Bellman-Ford算法执行步骤如下。

步骤1：首先初始化，将d(1)=0,d(i)=+∞，(2≤i≤n)， 把所有点存放到A中。

步骤3：算法在执行到偶数次迭代中，当集合A=∅时，算法停止，即可得到最短距离；当A≠∅，t=n-1时，可以得知负循环，算法停止；当集合A≠∅，k

步骤4：对于点i(1≤i≤n)， 当d0(i)=d(i)，t=t+1， 算法直接转到步骤2。

Bellman-Ford算法虽然可以应对负权重，但是不能求解有负循环的所有最短路径。如果负循环存在，在部分节点之间可能不存在最短路径。如图1所示，节点u，v之间因有1个负环路，所以不存在任何最短路径。

图1 负环路的u到v节点不存在最短路径

根据图1对Bellman-Ford算法进行改进，通过对v-1条轮降距操作，可以找出所有路径，为了验证是否存在负环路，对Bellman-Ford算法结束后在增加一轮降距检查，如果有d[v]>d[u]+w(u，v)的情况出现，则负循环存在。

改进的Bellman-Ford算法的伪代码如下：

Bellman-Ford-SHORTEST-PATHS-II(G,S)

(1)d[s]←0

(2)for v∈V-{s} do d[v]←∞

(3)for i←1 to V-1 do

(4) for edge (u，v)∈E do

(5) if d[v]> d[u]+w(u，v)then d[v]←d[u] +w(u，v)

(6)for edge (u，v)∈E do

(7) if d[v]> d[u] +w(u，v) then 报告负环路存在

4 改进算法在中药配送路径中仿真分析

本文以亳州地区中药连锁店为例，首先算法开始选择仓库作为配送路径的出发点，分别将中药配送到亳州市的3县1区共4个地区，根据改进的算法对其他节点的距离进行初始化，并将几个地点区域分别用字母表示(表1)。

表1 亳州三县一区地点

根据改进的Bellman-Ford算法对几个地区的中药配送路径进行选择，找到最佳的路径。改进算法中的(3)是Bellman-Ford算法的核心，一共执行了v-1次。算法第4行的内循环依次对每条边进行考虑，并进行相应的降距操作。边被考虑的次序是任意的，首先考虑的边是{B，E}，由于B的距离是∞，E的距离也是∞，而w(B,E)=2,2+∞=∞，因此E的距离维持为∞。同理，第2条边{D,B}也是同样的结果。第3条边是{B,D}，由于B的距离是无穷的，所以D的距离维持不变。第4条边是{A,B}， 由于d[A]=0,d[B]=∞，w(A,B)=-1, 而0+(-1)=-1<∞， 因此， 将节点B的距离降低到-1， 即d[B]=-1。第5条边是{A,C}，由于d[C]=∞,d[A]=0,w(A,C)=4, 而0+(4)=4<∞， 所以，调整d[C]=4。第6条边是{D,C}，由于d[C]=4，d[D]=∞，w(D,C)=5， 而5+∞=∞>4，因此，d[C]的值维持不变。第7条边是{B,C}， 由于d[C]=4，d[B]=-1，w(B,C)=3，而-1+3=2<4，因此，调整d[C]=2。第8条边是{E,D}，由于d[D]=∞，d[E]=∞，w(E,D)=-3，而-3+∞=∞，因此，d[D]的值保持不变。所有的边都考察了一次。第1轮循环结束。按照前面的顺序继续第2轮考察，再进行第3轮和第4轮循环，节点的距离没有发生任何改变，最终找到最短距离(图2)。

图2 最佳路径选择

5 结论与讨论

中药配送是药品服务行业中必不可缺少的一部分，有助于改善整体药品供应链的运行。本文对传统的Bellman-Ford算法进行了改进。仿真结果表明，改进的Bellman-Ford算法可以减少算法的存储空间，优化中药配送路径，从而降低配送成本，提高中药企业的利润。