自主学习和案例教学在概率论与数理统计教学中的应用

段宝彬，丁芳清，牛 欣

(合肥学院 人工智能与大数据学院，合肥 230601)

概率论与数理统计是普通本科院校各相关专业一门重要的公共数学基础课，对于学生数学素养的提高、后续专业课程的学习和随机实际问题的解决都起着举足轻重的地位。如何切实提高概率论与数理统计课程的教学质量，使学生能够灵活应用所学概率统计知识去解决专业或实际问题是本课程教学改革的一个重要方向。

1 概率论与数理统计课程目前的教学现状

1.1 重概率、轻统计

在概率论与数理统计课程的教学过程中，普遍存在着“重概率、轻统计”的现象[1]，主要表现在：

(1)课时分配上，概率论部分的授课学时远大于数理统计部分的授课学时，一般情况下，数理统计部分的授课学时仅为概率论部分的一半；

(2)许多与后续专业课程或实际应用紧密相关的一些数理统计内容未安排在课程教学计划中，如一元和多元回归分析、方差分析等；

(3)课程讲授时，概率论部分的例题和习题讲得多，数理统计思想和统计实例介绍得少。

1.2 重理论、轻应用

在介绍概率论与数理统计的相关知识时，基本概念、定理等理论部分介绍得比较多，与日常生活、学生所学专业结合的实际应用案例讲得比较少。主要原因为：一方面是本课程知识点多，课时紧张；另一方面大部分数学老师更擅长理论推导和分析，自身的实践应用能力也有待进一步提高。

1.3 重讲授、轻自学

从教学方式上看，大多采用粉笔板书的方式进行授课，也有部分采用多媒体方式授课的，但都以教师在课堂上讲授为主，学生被动地听，课堂互动不多，不能充分发挥学生的主体地位，对学生自主学习能力的培养还很欠缺。

1.4 重习题、轻实验

从概率论与数理统计的知识巩固方面看，大多数教师采用布置一定数量的习题(作业)让学生在课外完成，但对利用数学或统计软件解决实际问题的实验重视不够，甚至很多院校因为课时紧张等原因都没有安排相关的实验教学内容。通过做习题(作业)，虽然有助于学生对课程知识的理解，提高学生的运算能力，但对学生动手解决实际问题能力的提高不多，不利于应用型人才培养目标的实现。

1.5 重期末、轻过程

从考核方式上看，大多数高校采取“以期末考试为主，兼顾平时成绩”的成绩评定方式。这种考核方式容易造成部分学生平时不学习、考试前临时抱佛脚的情况出现；过程成绩主要根据学生平时的出勤、作业完成情况评定。由于平时作业有可能抄袭、课堂上也存在个别同学玩手机、睡觉的情况，因此，传统的过程成绩评定方式不能完全反映学生平时的真实学习情况。

为了解决概率论与数理统计教学中的上述问题，课程组尝试基于自主学习和案例教学的教学改革，结合概率统计在实际问题和专业中的应用，指导学生养成自主学习的习惯，充分发挥学生学习概率论与数理统计课程的积极性与主动性。

2 强化自主学习概率论与数理统计

在概率论与数理统计授课过程中，如何激发学生的学习兴趣，使学生由被动学习变为主动学习，充分发挥学生在概率论与数理统计学习中的主体地位，是概率论与数理统计教学改革的一项重要内容。[2]为了更好地促进学生自主学习，任课教师需要让学生明确自主学习的目标，制定具体的自主学习方案和实施细则，改进课程的考核方式，以相应的自主学习项目为驱动，及时检查、听取学生的汇报，并进行提问和学生答辩，进而完成自主学习项目的考核，这样就可以将学生的自主学习落到实处，切实提高概率论与数理统计课程的教学质量。

2.1 概率论与数理统计课程的自主学习目标

更好地理解和掌握概率论与数理统计的相关理论知识，提升学生的自主学习能力和实践动手能力，从而更好地学习后续专业课程和解决日常生活中遇到的复杂随机问题。

2.2 概率论与数理统计课程自主学习方案的设计

在概率论与数理统计的自主学习方案中，既有理论知识、概率论与数理统计产生的历史背景、统计思想等内容的自主学习，也有数学或统计软件的自主学习、相关实用统计方法的自主学习。以精心设计的3个自主学习项目为驱动，全面提高学生的自主学习能力、利用所学知识解决实际问题的能力、团队合作、沟通及表达能力。3个具体的自主学习项目如下。

项目1：概率统计的起源、发展历史及统计思想的综述；

项目2：概率论的基本概念、基本理论和方法的自主复习和巩固；

项目3：自主学习软件及实用统计方法在日常生活或所学专业中的应用。

2.3 概率论与数理统计课程自主学习项目的考核

在概率论与数理统计的课程总成绩中，除了统一的期末闭卷考试成绩(50%)和学习笔记等平时成绩(10%)之外，剩余的40%为自主学习考核成绩，其中每个自主学习项目的考核方式及其在自主学习考核成绩中的比例如下：

项目1的考核方式为开课后前四周之内每个学生提交自己的文献阅读综述报告，根据报告的内容和格式规范性评定成绩，该项目成绩占自主学习成绩的30%；

项目2的考核方式为概率论部分内容结束后进行闭卷测验，该项目成绩占自主学习成绩的30%；

项目3的考核方式为1—3名学生组成项目组，每组成员分工协作，互帮互助，共同完成该项目。课程结束后一周内每组提交相应的程序和课程论文，并制作ppt进行汇报和答辩，根据课程论文的内容、格式规范性、ppt质量和汇报、答辩情况综合评定成绩，该项目成绩占自主学习成绩的40%。为了鼓励学生积极参加相关的学科竞赛，对于参赛学生，只要竞赛时用到了概率统计的相关知识，允许他们直接用参赛的相关论文来进行自主学习项目3的考核。

3 案例教学在概率论与数理统计课程教学中应用

案例教学是以案例的形式介绍需要讲授的相关知识点，以活跃课堂互动氛围，使学生了解相关理论知识的应用场景。选取的案例要贴近现实生活，或者与学生所学专业密切相关，使学生真切体会到学以致用的乐趣。[3-4]下面通过三个案例探讨案例教学在概率论与数理统计课程中的应用。

3.1 三门问题

在讲授全概率公式和贝叶斯公式时，可以用经典的“三门问题”进行案例教学。该问题来自美国一个电视游戏节目，在编号为1、2、3的三个关闭的门后面分别放有一个汽车、两只山羊。参赛者只能选择其中一个门，若选择的门后面是汽车，则可免费获得该汽车；若选择的门后面是山羊，则可免费获得该山羊。假设主持人事先知道哪个门后面是汽车，如果参赛者选择的是1号门，但在未打开它的时候，主持人打开了2号门，显示该门后面是一只山羊。这时，主持人征询参赛者的意见，问他是否需要将当初选择的1号门更换为3号门。如果你是参赛者，你是否愿意更换呢？

从直觉上看，既然2号门后面不是汽车，1号门和3号门后面是汽车的可能性相同，是否更换当初选择的门，获得汽车的概率看起来应该相同，各为50%。实际情况真是这样吗？

下面就利用贝叶斯公式来解决这个问题。实际上，要回答是否更换选择的门，在已知2号门后面为山羊的条件下，需要分别计算1号门和3号门后面是汽车的条件概率，其中哪个条件概率大，就可以选择其对应的那个门作为最终的选择。

在主持人打开2号门的条件下，3号门后面为汽车的概率

可见，直觉有时候并不可靠，更换当初选择的1号门为3号门可以使免费获得汽车的概率增加1倍。

另外，也可以让学生在课外自主学习Matlab软件并编程随机模拟求解该问题，通过大量(比如100000次)的重复试验，在主持人打开2号门的条件下，分别统计1号门和3号门后面为汽车的次数，计算相应的频率。通过让学生亲自动手编程验证上述结论，可以进一步提高学生的实践能力。

3.2 开水房拥挤问题

在讲授中心极限定理时，可以引入关于开水房拥挤的案例。假设合肥学院二期宿舍楼入住学生为6000人，只配备一个装有50个水龙头的开水房，开水房开放时间为每天中午12∶00—13∶00和晚上18∶00—19∶00。假设每个学生每天打开水占用水龙头的平均时间为1.2分钟，可随机使用任一个水龙头打开水。由于同一时刻打开水人数较多，且水龙头较少，经常出现打开水拥挤排长队的现象。如果你是学校后勤管理人员，请你尝试解决如下两个问题：

(1)如果不增加水龙头，学生打开水需要排队的概率是多大？

(2)如果增加水龙头，需要新安装多少个水龙头，既可以缓解学生打开水排队现象，又不会产生因安装过多水龙头而造成浪费的现象？

(1)由题意，所求的概率为P(X>50)，由于X是服从二项分布的随机变量，直接计算这个概率比较麻烦.

由De Moivre-Laplace中心极限定理[5]，有

X～N(60,59.4) (近似地)

因此，如果不增加水龙头，学生打开水需要排队的概率大约是90.28%，拥挤现象非常严重。

(2)假设需要新安装水龙头的个数为a，可以使学生打开水排队的概率小于0.05，这样既可以缓解学生打开水排队现象，又不会产生因安装过多水龙头而造成浪费的现象，则有

因此，如果增加水龙头，需要新安装23个水龙头，使总的水龙头个数达到73，既可以缓解学生打开水排队现象，又不会产生因安装过多水龙头而造成浪费的现象。

另外，可以让学生课外利用Matlab软件编程计算在不同数量的水龙头下，学生打开水排队的概率，并绘制两者之间函数关系的图形，更加直观地观察开水房拥挤问题。

3.3 应届毕业生就业与考研人数比例的估计问题

在介绍参数估计时，可以引入毕业生考研与就业人数比例估计的案例。每个应届毕业生都面临毕业意向选择问题：考研或就业。假设某高校今年应届毕业生中考研人数为a，就业人数b=ka，即就业与考研人数的比例为待估计参数k。现从今年该高校应届毕业生中有放回地依次抽取n个学生进行毕业意向调查，得到简单随机样本X1,X2,…,Xn，则X1,X2,…,Xn相互独立，且与总体X同分布(0-1分布)。总体X的定义及分布如下：

在有放回抽取的n个应届毕业生中，假设经统计毕业意向为考研的人数为m.下面分别采用矩估计法和最大似然估计法对就业与考研人数比例k进行估计。

(1) 矩估计法。

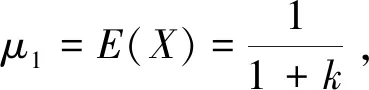
(2) 最大似然估计法。

设样本X1,X2,…,Xn的一组样本观测值为x1,x2,…,xn，则有

对应似然函数

对应对数似然函数

=(n-m)lnk-nln(1+k).

另外，该案例也可以用于估计工厂中合格品与次品件数的比例、某地区男性与女性人数的比例、水产养殖场中不同类型鱼条数的比例等。[6]

4 结 语

近几年，合肥学院概率论与数理统计课程组通过将自主学习和案例教学应用于教学实践中，学生学习概率论与数理统计知识的兴趣得到了很大的提高，学生学习的自主性更强，师生的课堂互动更频繁，学生的团队意识、应用意识、沟通与合作能力和创新能力均得到了较大提升。不仅概率论与数理统计课程期末考试的及格率也有了很大的提高，学生参加各种学科竞赛等课外实践活动获得全国及安徽赛区的各种奖项更多。以后打算将微课、基于网络的PBL教学等更多信息化技术应用于概率论与数理统计课程教学中，以进一步提高概率论与数理统计课程的教学质量。