Caputo-Fabrizio分数阶线性动力系统的可观测性和可控制性
赵正祥,李晓艳,刘 松
(安徽大学 数学科学学院,合肥 230601)
0 引 言
众所周知,动力学系统的可控性问题被广泛用于控制系统的分析和设计中。如果可以通过某个控制器,在相应的时间影响或控制与该过程相对应的每个状态,则可以说系统都是可控制的。可观性是通过了解系统的外部输出从而很好地推断系统内部状态的一种度量。系统的可观测性和可控制性是数学对偶关系。Kalm针对线性动力系统引入了可观性和可控性的概念。文献[1-3]等对整数阶线性和非线性动力系统的可控性及可观性进行了研究,并有了较为丰富的研究结果。对分数线性系统的可观性和可控性研究结果也在不断丰富。[4-7]学者M. Fabrizio[8]和A. Atangana以及D. Baleanu[9]在2016年提出新两种有非奇异核的分数阶导数,分别为Caputo-Fabrizio分数阶导数和Atangana-Baleanu分数阶导数,对于含有这两类方程的解的表达式及性质等问题的研究仍在进行中,但对含有非奇异核分数阶导数线性系统的可观性和可控性研究却少之又少。[10]本文将从非奇异核分数阶导数Caputo-Fabrizio分数阶导数出发对Caputo-Fabrizio分数阶线性动力系统的可观测性和可控制性进行研究,并通过Grammian控制观测矩阵给出并证明系统可观测和可控制性的充分必要条件。
本文将考虑如下Caputo-Fabrizio分数阶线性动力系统方程[11]
(1)
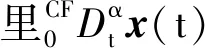
1 预备知识
本节介绍与论文有关Caputo-Fabrizio分数阶导数定义及相关引理。
定义1函数x∈H1(a,b),b>a≥0,α∈[0,1],定义为
(2)
其中H1(a,b)表示希尔伯特空间,B(α)表示归一化函数,满足B(0)=B(1)=1。
定义2函数x的Laplace变换定义为

定义3X的反Laplace变换定义为
这里c0位于拉普拉斯积分的绝对收敛的右半平面。
定义4单位脉冲函数δ(t)定义为
并且单位脉冲函数的Laplace变换
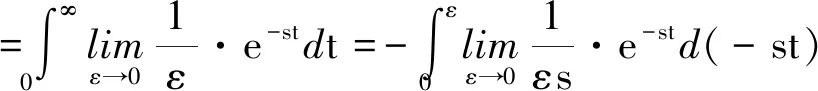
2 系统(1)的解的表达式
本节利用对Caputo-Fabrizio分数阶导数的Laplace变换,并借助单位脉冲函数δ(t)给出系统(1)解的表达式。
引理1Caputo-Fabrizio分数阶导数的Laplace变换结果为



定理1设[B(α)I-(1-α)A]是满秩的,那么系统方程(1)的解的表达式为
x(t)=B(α)[B(α)I-(1-α)A]-1eαA[B(α)I-(1-α)A]-1tx(0)+
证明将(2)式代入系统方程(1)可以得到
对等式两边同时使用Laplace变换根据引理2.1可得
这里X(s)=L[x(t);s],U(s)=L[u(t);s],x(0)=x0。整理(11)式得到

(3)
分别对(3)式两端使用反Laplace变换得到方程的解的表达式
x(t)=B(α)[B(α)I-(1-α)A]-1eαA[B(α)I-(1-α)A]-1tx0+
(4)
对(4)式进行化简,令R=[B(α)I-(1-α)A]-1有
(5)
3 系统(1)可控制性
定义5系统(1)在区间[t0,t1]是可控的,当且仅当对于任意一对向量x0,x1∈Rn,存在控制元u(t)使得系统(1)的解x(t)满足x(t0)=x0,x(t1)=x1。或称之为在区间[t0,t1]上,控制元u(t)使系统从x0状态转化为x1。
根据(5)式可以将系统方程的解进一步简化
x(t)=B(α)ReαARtx0+
这里令
可以得到
定理2系统(1)在区间[t0,t1]是可控的充分必要条件是可控Grammian矩阵

是正定的,这里T表示矩阵的转置。
证明假设M是正定的,那么M是非奇异的且M的逆存在,即M-1存在且有意义。给定输入控制元
u(t)=BTZTM-1[x1-B(α)ReαAR(t1-t0)x0].
(6)
给定系统(1)解x(t)的初始条件x(t0)=x0,那么方程解的表达式为

(7)
把(6)式代入(7)式可得

B(α)ReαAR(t1-t0)x0+MM-1[x1-B(α)ReαAR(t1-t0)x0]=x1.
也就是说系统(1)是可控的。
另一方面,假设M是非正定的,那么必存在一个非零元y满足
yTMy=0,
也就是说

这表示在区间[t0,t1]上yTZ(t1-s)B=0。令x0=[B(α)ReαAR(t1-t0)]-1y。根据假设存在控制元u(t)在区间[t0,t1]上将系统状态由x0转化到原点
将x0=[B(α)ReαAR(t1-t0)]-1y代入并且等式两边同时左乘yT可得
由前文知,上式的第二项是零,若要等式成立则yTy=0,但是y是非零元即y≠0。所以M是正定的。
4 系统(1)的可观测性
在判断系统(1)的可观测性时,无须考虑控制元u(t)的影响,系统将变成如下形式

(8)
这里α∈[0,1],x(t)∈Rn,A是一个n×n的常矩阵。
根据定理2可得
x(t)=B(α)ReαAR(t-t0)x0。
(9)
令Q(t-t0)=B(α)ReαAR(t-t0),原式化简为
x(t)=Q(t-t0)x0。
(10)
在区间[t0,t1]上存在一个观测函数h(t),h(t)∈Rm,H是一个m×n的常矩阵,满足
h(t)=Hx(t)。
(11)
定义6如果
h(t)=Hx(t)=0,t∈[t0,t1],
并且
x(t)=0,t∈[t0,t1],
那么在区间[t0,t1]上系统(8)和系统(11)是可观测的。
定理2系统(8)和系统(11)在区间[t0,t1]上是可观测的充分必要条件是观测Grammian矩阵

是正定矩阵。
证明给定初始条件x(t0)=x0,根据(9)式和(10)式可得
h(t)=Hx(t)=HB(α)ReαAR(t-t0)x0=HQ(t-t0)x0,
那么h模的平方为

5 结 论
可观性是通过了解系统的外部输出进而很好地推断系统内部状态的一种度量,而可控性则告诉我们有关更改系统状态以在给定时间间隔内采用预定值的能力。对分数阶动力系统的可观性和可控性的研究对于许多实际日常应用都是重要的问题。我们通过使用Grammian控制观测矩阵证明了Caputo-Fabrizio分数阶线性动力系统的可观性和可控性有关的两个新的主要结果。对非奇异核分数阶微分方程有关控制观测理论方面提供一些参考。

