基于LSTM的软刚臂单点系泊力预测方法研究

韩 宇，黄国良，李 鹏

(中海油能源发展股份有限公司采油服务分公司 天津300452)

0 引言

FPSO(Floating Production Storage and Offloading Unit)在我国渤海湾有着广泛的应用。FPSO不同于一般的船舶，本身没有动力系统，通常靠系泊系统定位在某一固定海域，在恶劣的海况下不可以完全避航，因此荷载是其主要的设计指标之一。但是系泊系统对环境荷载的承载能力是有限的，在极端恶劣情况下需要进行解脱来避免受到永久性破坏，这时对系泊力的预报就显得十分重要。要准确地预报系泊力，需考虑FPSO与系泊系统之间的耦合作用，还需要准确估算系统的黏性阻尼，目前的水动力学理论数值分析还不能很好地解决这些难题。对于模型实验，过小的模型会存在严重的缩比效应，而水池实验对环境要素的模拟也存在诸多不足，故模型实验的结果也不尽如人意。尤其对于渤海的FPSO，由于渤海水深基本在40 m 左右，属于浅水，对FPSO运动、受力的预报还要考虑浅水波非线性的影响，而目前对浅水效应的力学机理研究还不成熟，基于理论数值分析和模型实验的系泊力预报都存在一定的局限性。

通过对现场实测的浅水FPSO系泊力及其影响要素进行分析，发现系泊力和多个要素间存在复杂的关系。常用的分析方法，由于模型的多元性和非线性，对数据的完备性以及工程人员的理论水平要求较高，预报过程繁琐复杂，预报精度也难以保证。因此，找到一种精度较高，使用简便的系泊力预报模型就成为工程实践中的现实问题。

人工神经网络由于有联想记忆、分类识别、优化计算、非线性映射等功能，从20世纪90年代开始广泛应用于船舶与海洋工程预报领域。多位学者应用人工神经网络进行了受随机波浪力作用下的海洋平台的振动主动控制等研究。因此，拟将数值数据作为学习样本，建立人工神经网络模型，通过调整函数的扩展速度、对样木进行预处理和改进学习算法等措施，提高学习效率和预报精度。

1 长短期记忆神经网络模型(LSTM)

长短期记忆(Long Short-Term Memory，LSTM)

网络是循环神经网络的一个变体，可以有效地解决简单循环神经网络的梯度爆炸或消失问题。LSTM网络的循环单元结构计算过程为：①首先利用上一时刻的

外部状态ht-1和当前时刻的输入xt，计算出3个门，以及候选状态c~t；②结合遗忘门ft和输入门it来更新记忆单元ct；③结合输出门ot，将内部状态的信息传递给外部状态ht。

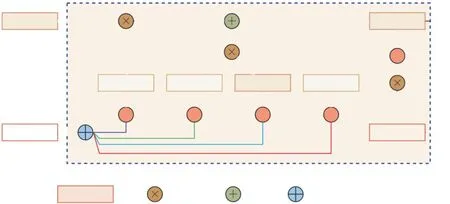
图1 LSTM循环单元结构Fig.1 Cycle element structure of LSTM

循环神经网络中的隐状态h 存储了历史信息，可以看作是一种记忆(memory)。在简单循环网络中，隐状态每个时刻都会被重写，因此可以看作是一种短期记忆(short-term memory)。在神经网络中，长期记忆(long-term memory)可以看作是网络参数，其中隐含从训练数据中学到的经验，且更新周期要远远慢于短期记忆。而在LSTM 网络中，记忆单元c 可以在某个时刻捕捉到某个关键信息，并有能力将此关键信息保存一定的时间间隔。记忆单元c 中保存信息的生命周期要长于短期记忆h，但又远远短于长期记忆，因此称之为长的短期记忆(long short-term memory)。

2 单点系统神经网络训练数据

在实船与数值模型一致性检验后，首先开展软刚臂系泊FPSO在时域中的耦合分析，得到FPSO运动与软刚臂受力实例，形成系泊力样本库；然后，按工况将FPSO位移(六自由度：纵荡，横荡，垂荡，横摇，纵摇，艏摇)作为原始特征值(用于神经网络输入)，软刚臂各节点受力作为原始标签值(用于神经网络输出)，分成训练集和检验集。将训练集通过长短时神经网络模型(LSTM)训练出对应的神经网络权重和偏置系数库，通过检验集校验神经网络系数库的准确度和响应时间。

在分析中，FPSO船体与软刚臂分别编号，为方便识别，分别设置“1”代表FPSO船体，“2”代表右系泊腿，“3”代表左系泊腿，“4”代表软钢臂，“5”代表系泊塔架(图2)。

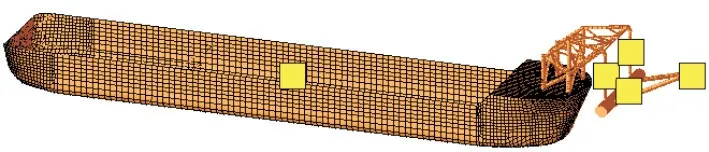
图2海洋石油113 FPSO模型示意图Fig.2 Sketch of HYSY 113 FPSO model

为保障训练出的神经网络估算值准确且训练过程快，在训练集的选取中，需要训练数据的覆盖面足够广(大致包含所在工况下FPSO船体与软刚臂运动的可能情况)、足够均匀(该工况下所有的运动响应都应有足够的数据量进行描述，避免对个别极值造成“淹没”)。训练神经网络的训练集以数值模型数据为主，对训练好的神经网络进行检验的检验集以数值模型数据为主，对检验好的神经网络进行验证的验证集以实测数据为主。

2.1 单点系泊神经网络基本模型建立

深度学习的目的在于发掘FPSO运动、环境条件和系泊力的内在关系，并将这种关系通过系数矩阵的方式进行表达。在使用中，先搭建基本的模型，初步调整神经网络的构架，通过对比选择较好的神经网络层数、每层的神经网络单元个数、激活函数、正则化方法等，再通过调整训练集的原始特征值，对数据进行认为的特征提取等方式进一步提高估算效果，通过挖掘数据特征而不是对神经网络的构架进行挖掘来提高神经网络的估算效果。

本次建立神经网路模型的版本及环境为：系统win10；显卡NVIDIA GeForce CTX 1080 Ti；CUDA 10.0；cuDNN 10.0；Anaconda 环境管理器64位；Packages Python3.6；Tensorflow 2.0。

核心函数为：tensorflow.keras.layers.LSTM()，在tensorflow 框架下，设定长短时神经网络单元。其中，激活函数取tanh；reuse设置为Ture，范围内重用变量；前面几层的LSTM 神经元中return_sequences 设置为Ture，最后一层设置为False，是否返回所有序列状态的输出；dropout 取0.2，recurrent_dropout 取0.2，训练中每次更新参数时随机丢弃神经元比例，只有LSTM层设置；forget_bias_init 取one，遗忘门偏置的初始化函数；inner_activation 取hard_sigmoid，内部单元激活函数；state_is_tuple接受和返回状态设置为Ture；kernel_regularizer 取 keras.regularizeers.l2(0.01)，对该层中权值进行正则化；activity_ regularizer 取keras.regularizers.l1(0.001)，对该层中输出进行正则化；dtype设置为tf.float32；initial_state

设置为init_state，用于权重和投影矩阵的初始化。

添加输入层和输出层，建立长短时神经网络的基本模型，输入神经元个数和输出神经元个数根据所需输出数据界定，后续进行说明。输入输出层：权值以均值为0、方差为1进行初始化，偏置以参数0.1进行初始化。隐藏层：初始化通过tf.global_variables_ initializer 函数设定。

2.2 单点系泊数据归一化

输入输出数据的归一化处理可以避免一些不必要的数值问题。不同的输入输出数据往往具有不同的量纲和单位，如在本次的神经网络模型构建中，输入的6自由度中，有位移，也有转角，对输入输出数据进行归一化处理，可以消除各数据间的量纲影响，使各数据间具有可比性。

常用于时域数据处理的归一化方法有最大-最小标准化、Z-score 标准正态化等。

最大-最小标准化是对原始数据进行线性转换，将原始值映射到区间[0，1]之间。

式中：x 表示原始值；xmin和 xmax分别是该数据长度下的最大值和最小值；x′表示归一化后的值。

Z-score标准正态化是基于原始数据的均值和标准差进行的数据标准化，经标准化后的数据，其均值为0，方差为1。

式中：x 表示原始值；μ表示该数据长度下的均值；σ表示该数据长度下的方差；x′表示归一化后的值。

2.3 特征提取方法

对输入的数据进行分析，从统计的角度，可以看出其大致服从正态分布；从直观的角度看，其大致可以视为由高频和低频共同组合而成(图3)。

因此，针对该FPSO运动响应的单点系泊力计算中，提出了对输入数据进行特征提取，采用一阶矩和二阶矩的特征提取方法，从数值上描述其在所处的时间段中波动的唯一性。

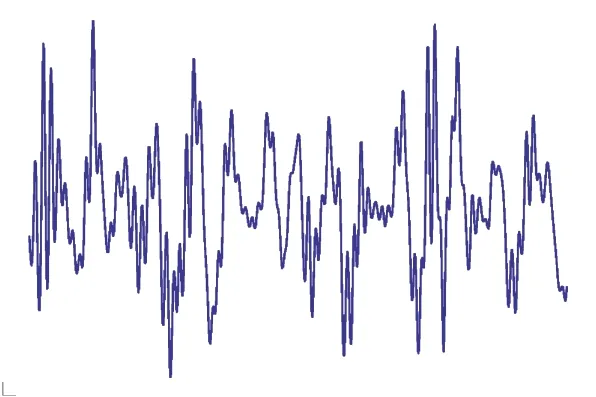
图3 输入数据船体x 方向运动情况Fig.3 Input data of ship motion in direction x

一阶矩和二阶矩的提取方法为：

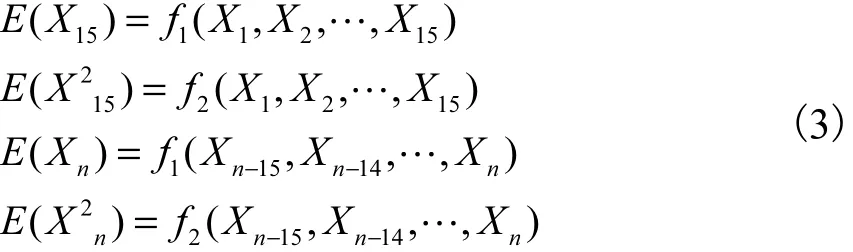
式中：E ( X15)表示第15个时间节点的数据对应的一阶矩的值；E(X215)表示第15个时间节点的数据对应的二阶矩的值；X1, X2,…,X15分别表示第1，2，…，15个时间节点上经归一化处理后的值；E ( Xn)表示第n个时间节点的数据对应的一阶矩的值；E ( X2n)表示第n个时间节点的数据对应的二阶矩的值；f1()表示求一阶矩的函数；f2()表示求二阶矩的函数。

之所以选取15个时间节点，是因为1个高频的波动周期长度均值在20 s左右。再将第n个时间节点上的船体6自由度数据与一阶矩、二阶矩进行组合：

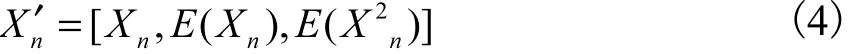
式中：Xn表示第n个时间节点上，船体的6自由度；表示第n个时间节点上，船体的6自由度与一阶矩、二阶矩。

3 软刚臂单点系统深度学习

动态神经网络训练和检验的数据来源于数值计算，采用OrcaFlex 软件在时域下计算FPSO船体与软刚臂的动态响应。选取的环境海况为：波高3.4 m，周期8.4 s，波向100°，风速18 m/s，风向115°，流速1.34 m/s，流向115°，模拟时间10800 s。

在深度学习过程中，选取数值稳定后1～8000 s的运动时程响应数据作为动态训练集，用于训练动态神经网络；选取8000～8500 s 的运动时程响应数据作为动态检验集(图4)。在完成训练动态神经网络模型后，将其用于检验动态神经网络模型的估算效果。

图4训练集原始特征值(FPSO 6自由度)Fig.4 Original characteristic value of training set(6 DOF of FPSO)

训练集和验证集中的数据需要经过归一化处理和数据特征提取2个步骤。FPSO运动特征(6自由度)经2个步骤处理后作为神经网络的输入值，软刚臂受力经2个步骤处理后作为神经网络的输出值。未处理时，将FPSO的运动特征(6自由度)称为原始特征值，将软刚臂受力称为原始标签值(图5)，经归一化处理后称归一化后特征值和归一化后标签值，经数据特征提取后称神经网络输入值和神经网络输出值。神经网络计算出的结果还需要进行反归一化操作后，才能与原始标签值进行比较，将神经网络计算出的结果称为神经网络输出值(未反归一化)，将神经网络输出值进行反归一化操作后的结果称为神经网络估算值(反归一化后)。

按Z-score 标准正态化方法对原始特征值和原始标签值进行归一化处理，消除各数据间的量纲影响。将数据处理为均值为0、方差为1的值。

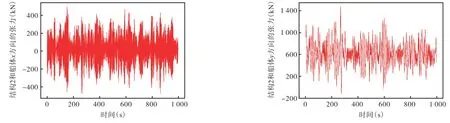
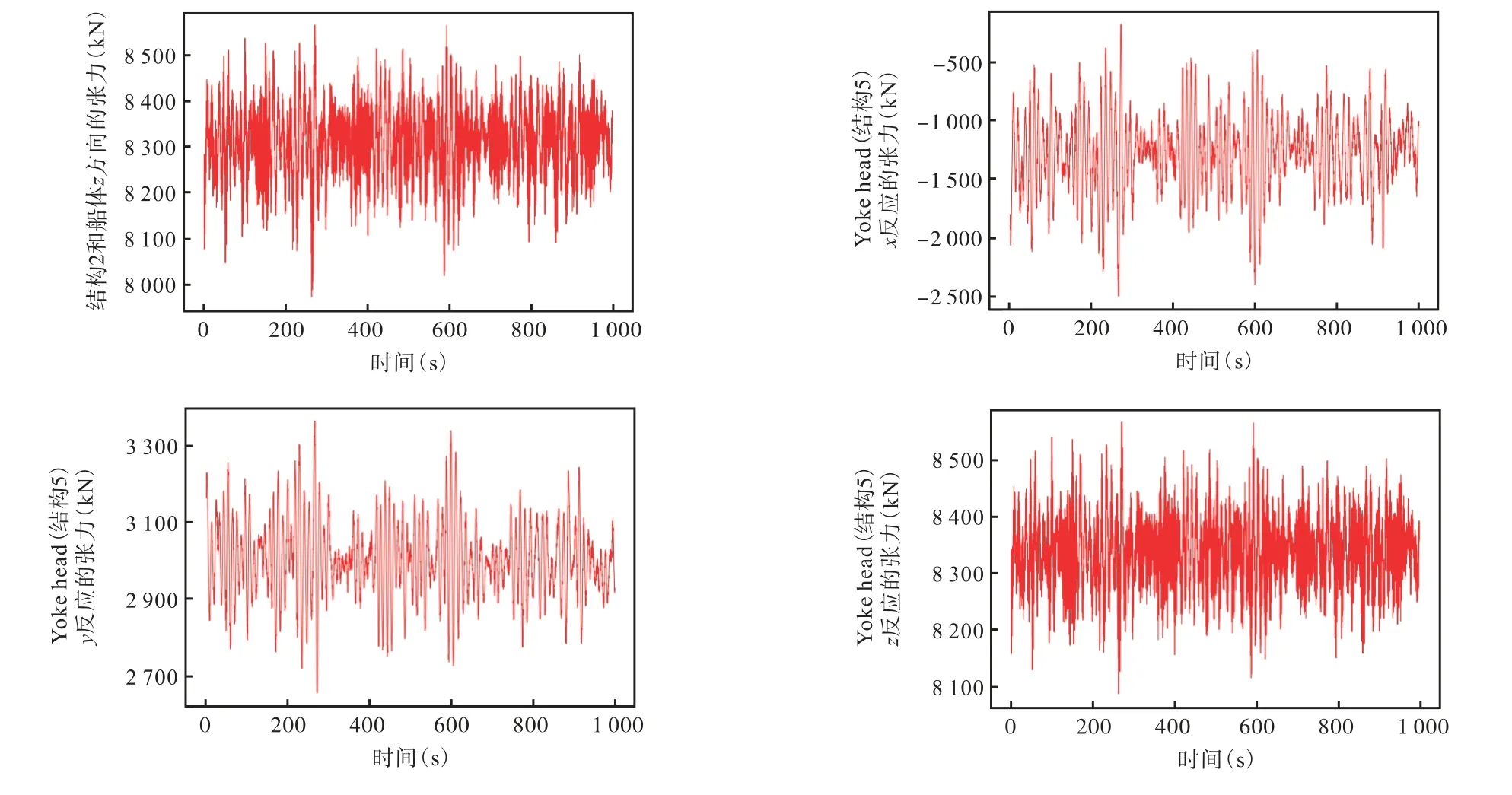
图5训练集原始标签值(2号系泊腿与船体、Yoke头张力等)Fig.5 Original label value of training set(number 2 mooring leg，hull and tension of yoke head)

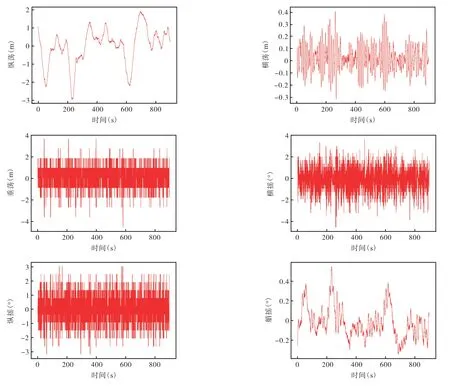
图6 训练集归一化后特征值(FPSO 6自由度)Fig.6 Characteristic value of training set after normalization(6 DOF of FPSO)

按特征提取方法对归一化后特征值从统计的角度进行人为的一阶矩二阶矩的特征提取，以描述每个数据在其所处时程阶段上的波动特征，并将其与归一化后的特征值整合，作为神经网络输入值训练神经网络(图6)。

神经网络计算出的数据对应的是输出值，需要进行反归一化操作，乘方差加上均值，加上量纲，将其转化为对应原始标签值的神经网络估算值(图7)。

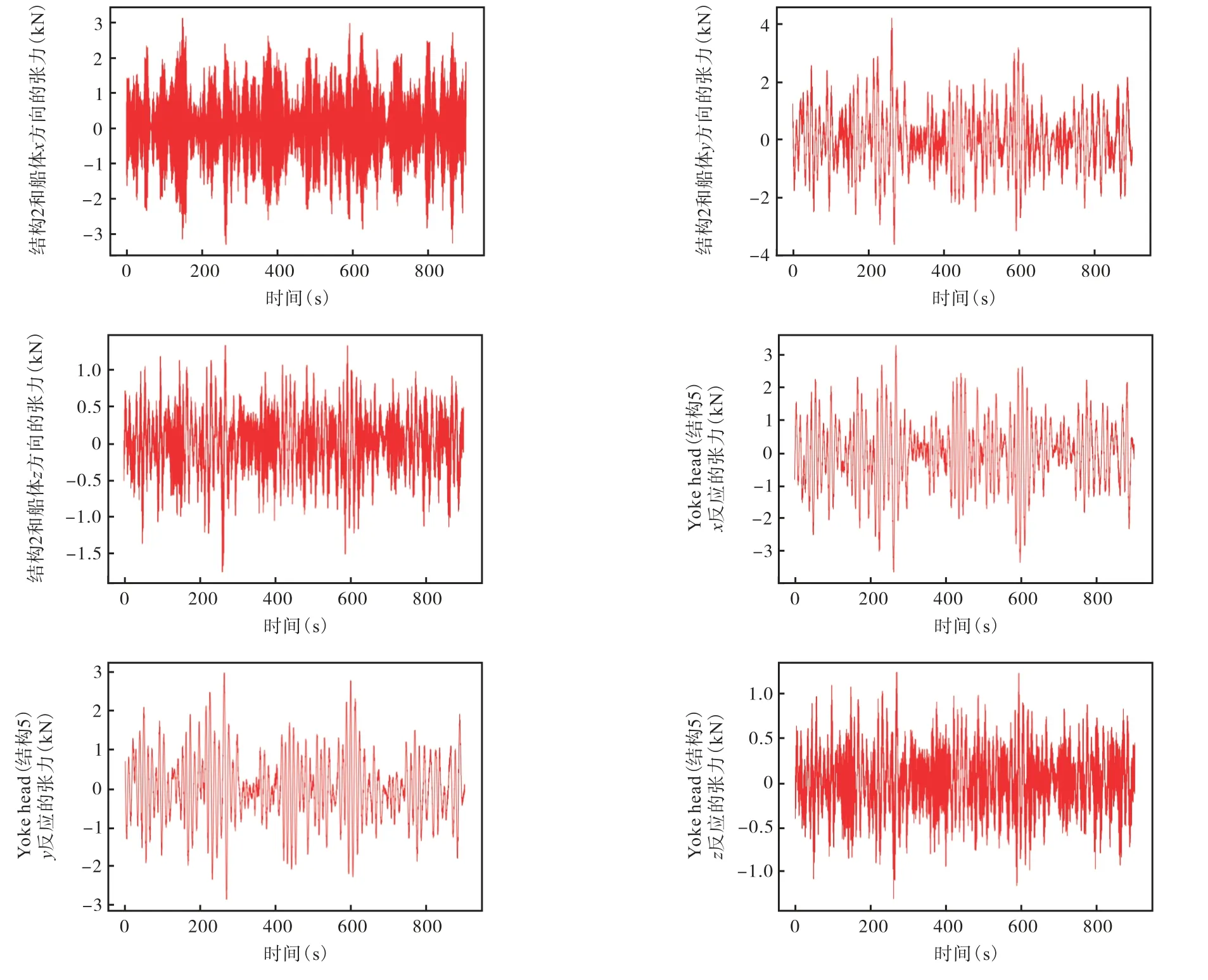
图7 训练集归一化后标签值(2号系泊腿与船体、Yoke头张力等)Fig.7 Characteristic value of training set after normalization(number 2 mooring leg，hull and tension of yoke head)

选取右系泊腿和船体在纵荡方向的受力进行分析。使用训练集训练好神经网络后，采用2种方法对神经网络的计算效果进行检验：①直接将原始数据标签值和神经网络估算值进行对比；②原始数据标签值和神经网络估算值的4种统计参数对比。

将训练集作为输入，带入神经网络检验结果。其目的是检验神经网络再次遇见与训练集相同的数据时，是否有能力准确计算出精确的结果(图8)。

对预测结果进行统计计算，采用4种统计方法，统计结果包括基于时程响应的平均值误差、标准差误差、极值误差和拟合度，统计结果如表1所示。

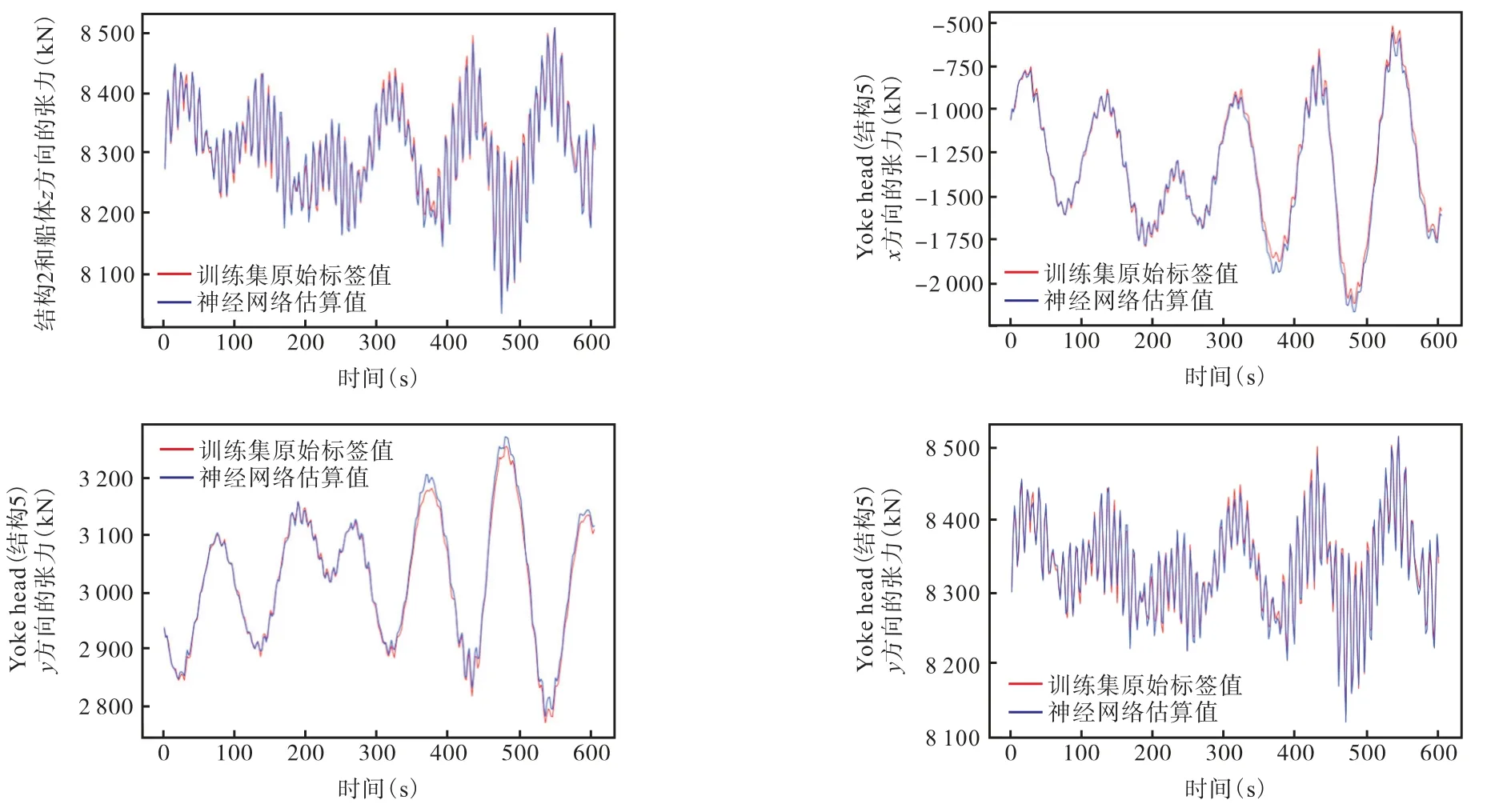
图8单工况下FPSO动态神经网络模型自检计算结果Fig.8 Self-check result of FPSO dynamic neural network model under single condition

表1神经网络模型自检结果统计值Tab.1 Statistics of self-check result of FPSO dynamic neural network mode l

表1中右系泊腿和船体间x 方向张力(kN)在平均值误差和拟合度上有较大误差，原因是其均值较接近0，在分母较小时，平均值计算容易出现较大的值。该结果表明该动态神经网络遇见和训练集相同的数据时，该神经网络计算出的结果非常精确。

4 结论

利用长短期记忆神经网络和浮体系统耦合数值模型建立了软刚臂单点系泊系统受力的实时预测模型。在应用中取得了较好的结果，形成结论如下：

①LSTM 模型适合处理软刚臂单点系泊系统的时序性数据，准确度较高。

②LSTM 模型层数增加没有明显改进预测的准确度，在模拟中，在Keras 中设置的units数量对结果的精度改进较大。

③在LSTM模型多层的堆叠中，应当设置return_sequences为True，以便将前一层的输出体现到下一层中。

④针对模拟中的过拟合现象，通过dropout 参数舍弃部分数据，增强正则化，有利于模拟结果准确度的提高。