26 m射电望远镜副面调整机构误差分析

古丽加依娜·哈再孜汗，项斌斌，王娜，艾力·玉苏甫，陈卯蒸，李宁，薛飞

1. 中国科学院 新疆天文台，乌鲁木齐 830011

2. 中国科学院大学，北京 100049

新疆乌鲁木齐南山射电望远镜(Nan Shan Radio Telescope, NSRT)是一台26 m口径全可动射电望远镜，采用 Stewart 并联机构[1]对其副反射面(简称副面)进行空间五自由度位置(x、y、z方向平移，x、y方向转动)精确调整。并联机构具有定位精度高、刚度大、结构稳定、承载能力强、运动惯量小、动态特性好等特点[2-5]，已成功应用于精确指向平台、隔振平台、太空望远镜次镜头与主镜头的实时对齐平台、空间对接装置以及射电望远镜副面调整机构等许多方面。近几年国内外建成的射电望远镜大都使用并联机构作为副面调整机构，例如国外 ALMA (Atacama Large Millimeter Array)[6]、GBT (Green Bank Telescope)[7]、Effelsberg[8]及国内 FAST (Five-hundred-meter Aperture Spherical Telescope)[9]、天马[10]等。天线副面位姿调整是确保射电望远镜天线高精度指向的关键技术之一[11]。由于并联机构结构的复杂性，存在并联机构的制造和装配误差、形变误差、机构传动误差、回零误差等，导致并联机构运动到目标位姿时的预期值和实际值之间存在较大偏差，严重影响了并联机构的精度。NSRT改造之后的一段时间，对其进行不同波段转换时，时常出现天线指向偏差过大的情况，初步判断由副面并联机构运动误差引起，迫切需要对其进行误差分析，找出误差源并对并联机构进行误差补偿，从而提高并联机构的位姿精度。

为提高并联机构的位姿精度，需要对误差进行分析，建立精确的误差模型。Masory等[12]研究了传感器误差及关节中心位置加工误差的影响。Ehmann等[13-14]进行了一阶和二阶的误差分析。Jelenkovic和Budin[15]使用 Ehmann 的模型对并联机构进行了误差分析。Tischler和Samuel[16]给出了计算关节回差影响的数值方法。Pott和Hiller[17]提出了一种计算关于某个位姿定位误差的通用方法。Ahmad等[18]采用解析法分析了在外部载荷下铰链变形引起的定位误差。Zhou等[19]提出了一种基于 D-H 矩阵微分的误差模型。李健等[20]使用消元法求解并联机构所有关节变量的方法，建立了仿咬合并联机器人的误差模型。姚蕊等[21]对 FAST 馈源仓 Stewart 调整平台进行了精度分析。针对零点位置误差，李毅[22]的研究表明并联机器人的运动精度主要受几何误差源的影响，基于对误差源传递系数的分析，指出其零点误差对末端位置误差的影响远高于其他几何误差源。郭云鹏等[23]运用空间矢量法建立了六自由度并联机构的零点误差模型。孙月海等[24]以Delta并联机构为例，提出了一种基于视觉测量的零点标定方法。

本文在上述研究的基础上，针对NSRT副面并联机构出现定位误差偏大的问题，用矩阵微分法建立了并联机构误差模型，通过误差仿真实验，研究了杆长误差、铰链误差及回零误差对并联机构末端精度的影响。用Leica激光跟踪仪测量了NSRT副面并联机构的运动精度，对比实测结果与误差模型的仿真结果，确定了影响并联机构末端位姿精度的主要误差源。

1 系统组成

如图1所示，NSRT副面并联机构的定平台与射电望远镜的副面支撑结构相连；副面与并联机构的动平台相连，由动平台带动副面进行五自由度运动。馈源仓安置于主面，射电望远镜不同的工作波段对应不同的馈源，通过副面及并联机构的运动调整副面的位姿，使微波信号经过副反射面的二次反射后进入相应馈源，这就要求副反射面的焦点与预定工作馈源的相位中心实现精确对焦。

如图2所示，并联机构主要由动平台、定平台、上下虎克铰、运动控制器及连接于动平台和定平台之间的6套伺服电机控制的电动缸构成。电动缸与动平台及定平台均采用间隙小、可承受大载荷的两自由度虎克铰链接，通过6个电动缸的协调伸缩实现并联机构动平台在空间的五自由度运动。其运动范围为：x、y方向平移±50 mm、z方向平移 ±80 mm；绕x、y轴旋转角度±5°。在天线0°～90°任意姿态下，动平台的重复精度：线性误差小于0.07 mm；角度误差小于0.01°。

图2 NSRT副面Stewart并联机构

2 误差建模

并联机构位置姿态的高精度控制是实现精确运动调节的前提。机构末端的实际位姿与理论位姿之间的偏差，称为系统的位姿误差。对平台进行精度分析时，需要对误差源及其影响进行分析，建立误差模型，对影响较大的误差源进行补偿。

对并联机构进行误差分析时主要考虑机构本身因素的误差影响，包括几何误差和回零误差。几何误差包括动、定平台上的铰链误差及六分支杆杆长误差。回零误差主要指回零操作过程中，由增量式编码器与限位开关相结合的回零检测装置反馈信号的异常，造成并联机构零点位姿的偏差。

2.1 几何误差建模

(1)

式中：c11=cosαcosβ；c12=cosαsinβsinγ-sinαcosγ;c13=cosαsinβcosγ+sinαsinγ;c21=sinαcosβ;c22=sinαsinβsinγ+cosαcosγ;c23=sinαsinβcosγ-cosαsinγ;c31=-sinβ;c32=cosβsinγ;c33=cosβcosγ。

对于闭环矢量OB-bi-pi-OP-OB有：

(2)

(3)

(4)

图3 并联机构坐标系统

式(4)简化成矩阵形式为

(5)

Δl=JPΔe+JCΔd

(6)

(7)

JC=

(8)

在并联机构的工作空间内JP是可逆的，因此并联机构的位姿误差为

(9)

2.2 回零误差建模

NSRT副面并联机构的电机采用增量式编码器进行电机转角指示。由于增量式编码器不能提供绝对位置，因此需要通过回零找到预定义的参考位置。并联机构的参考位置也称零点，是机构各坐标预先指定的位置，该位置通常作为各坐标轴的原点，是机构运行的逻辑起点。NSRT副面并联机构支腿的两个极限位置装有限位开关，支腿的零点是以限位开关为基准的相对位置，回零过程中的限位开关是机构回零信号的反馈装置。因此，限位开关反馈信号的异常会导致并联机构回零不准。此外，由初始安装工艺水平造成的偏差及机械磨损引起的误差累积也会造成零点位置的偏差。

一方面，由于采用增量式编码器，控制过程中的反馈量是相对零点的增量式反馈，回零误差无法通过控制补偿，在机构工作过程中始终引起末端位姿的偏差。另一方面，由于采用增量式编码器，机构断电之后编码器不会对原有坐标轴的位置进行自动记忆与保存，系统每次断电前自动记录当前动平台指令位置，并以此作为下次上电后的实际位姿，然而由于指令位姿与实际位姿之间存在的误差会随着重新上电次数的增加不断累积，需要通过回零操作消除该累积误差。因此，提高回零精度对系统精度的提高至关重要。

并联机构执行回零操作是通过控制每个支腿上的驱动关节回到零点来完成末端动平台的回零，因此并联机构回零误差模型为

(10)

具体形式为

(11)

虽然回零误差及杆长误差都是通过杆长影响末端位姿，数学上回零误差模型和杆长误差模型是等效的，但实际工作过程中回零误差和杆长误差产生的原理不同，引起的末端位姿误差分布不同。回零误差是回零操作过程中产生的零点位姿的偏差，回零操作的目的是重新确立参考点与坐标轴的位置，能够使各项控制操作任务重新回到零点坐标，为后续的工作提供一个基准点，一旦这个基准点有偏移，将引起后续所有的工作点的偏差。而杆长误差受滚珠螺旋副传动误差的影响，对末端位姿的影响与驱动杆的行程相关，随杆长的变化在一定范围内变化。

3 实验研究及结果分析

为了分析影响 NSRT副面并联机构的误差源，分别对并联机构进行了仿真实验和实际测量实验。通过仿真实验分析了杆长误差、铰链误差及回零误差对并联机构末端位姿的影响。实际测量用激光跟踪仪获得了NSRT副面并联机构末端动平台的运动精度。将实际测量结果与仿真结果进行分析比较，确认了影响并联机构末端位姿的主要误差源。

3.1 几何误差模拟

本节对并联机构的杆长误差和铰链误差对末端位姿的影响进行仿真分析。首先对杆长误差、铰链误差进行随机抽样模型的构建，再将误差随机量带入误差模型得到最终结果。

1) 支腿杆长误差随机量抽样

杆长误差主要由滚珠螺旋副的传动误差、受力变形误差及加工误差引起；传动误差主要源于滚珠丝杠副的轴向间隙及螺距累积误差。对NSRT副面并联机构来说，在出厂时电动缸的精度小于0.01 mm，运动范围不大。安装3年以来运动次数约为700 次(平均1.5天换一次馈源)，估算并联机构整个传动部分的间隙小于0.04 mm，且并联机构工作时基本承受单向载荷，因此基本可以忽略传动间隙的影响，仅需考虑螺杆的螺距累积误差。此处假设支腿杆长偏差在公差T带内服从零均值正态分布，且相互独立。按照3σ原则，支腿杆长误差的标准差为

(12)

至此，可按正态分布抽样公式得到驱动杆杆长误差的模拟值：

(13)

式中：z1i和z2i为 (0,1) 间的伪随机数。

2) 铰链误差随机量抽样

铰链误差主要有动、定平台铰链空间安装位置误差和铰链制造误差引起的铰链中心位置误差及铰链间隙误差。NSRT副面并联机构采用双端虎克铰式并联机构，而虎克铰存在2个垂直方向的轴承(图4中的轴1和轴2)间隙误差，分别为轴孔与轴配合时存在的间隙。因此，铰链中心位置误差及铰链间隙误差的随机抽样模型为

(14)

式中：ω、γ在 [0,π] 内均匀分布，θ、φ在 [0,2π] 内均匀分布，且ω、γ、θ、φ相互独立;h为轴承间隙。

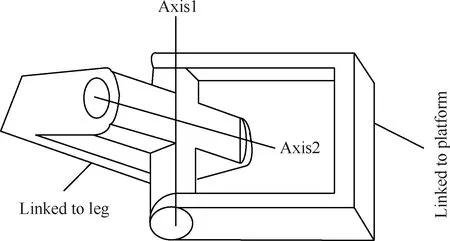
图4 虎克铰结构

3) 仿真实验

动、定平台铰链分布如图5所示。定平台铰链分布圆半径R=600 mm，动平台铰链分布圆半径r=358 mm, 初始位置动、定坐标系原点之间的距离为733 mm。

图5 NSRT副面并联机构铰链分布(单位：mm)

根据副面并联机构的结构参数，定量分析杆长误差和铰链误差对并联机构末端位姿的影响。假设分支杆杆长公差T=0.1 mm，铰链误差h=0.1 mm，样本容量为300，对并联机构末端位姿误差进行统计模拟。

模拟结果如图6～图8所示，受支腿杆长误差的影响，并联机构的位置误差为0.03 ～0.08 mm，为支腿杆长误差的3/10～8/10；受铰链误差的影响，并联机构位置误差为0.06～0.12 mm，为铰链误差的6/10～12/10；共同作用时并联机构的位置综合误差为0.06～0.15 mm。通过在整个工作空间上搜索并联机构末端位姿误差可知，如果保证杆长误差小于0.08 mm，铰链误差小于0.05 mm，即可保证并联机构在精度要求范围内。

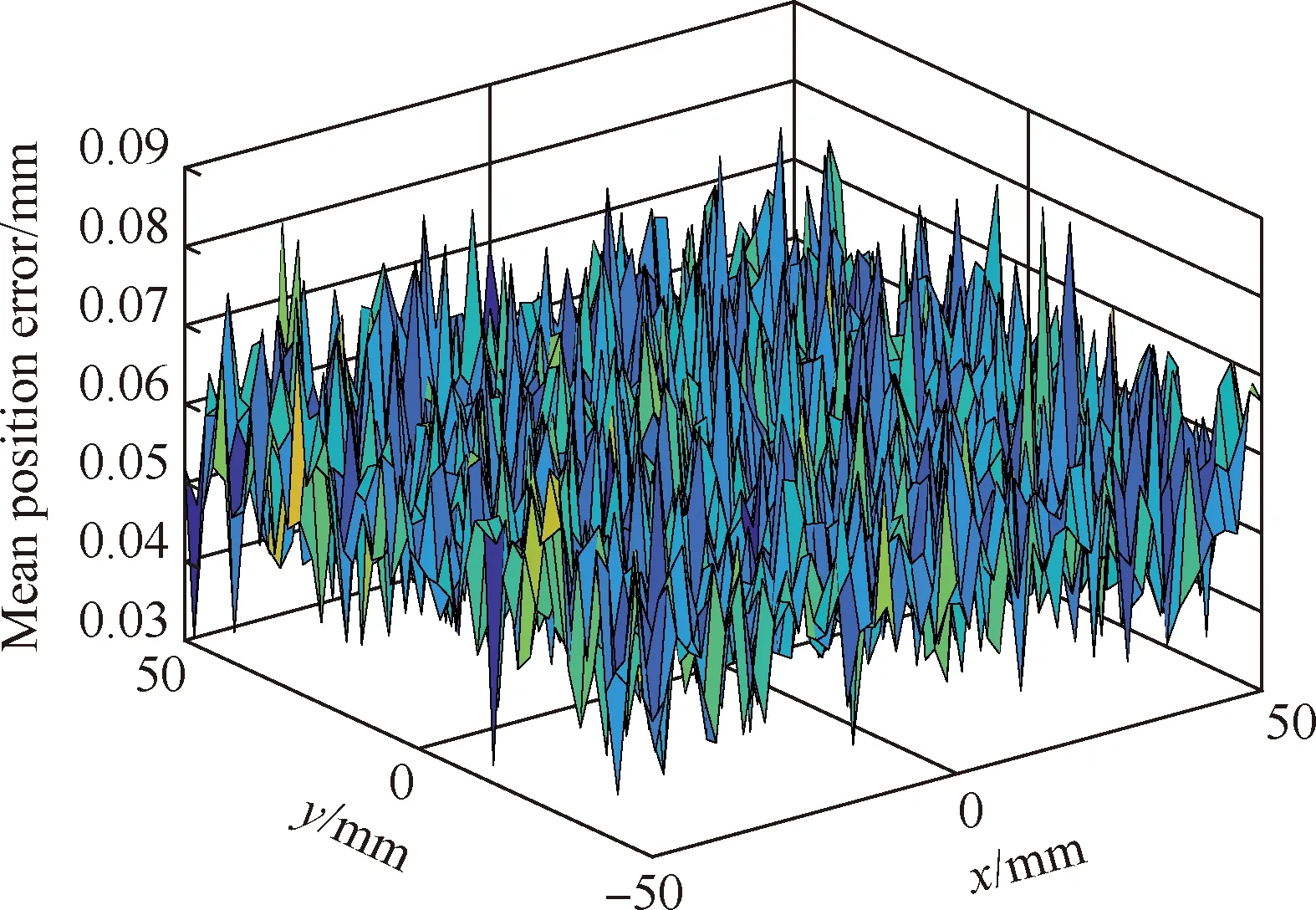
图6 只考虑杆长误差对Stewart并联机构位置误差的影响(z=733 mm)

图7 只考虑虎克铰链误差对Stewart并联机构位置误差的影响(z=733 mm)

图8 考虑杆长误差和虎克铰链误差对Stewart并联机构位置误差的影响(z=733 mm)

3.2 回零误差模拟

为了研究支腿的回零误差对末端回零位姿的影响，这里给每个支腿施加从±0.05～±0.1 mm 各个区间内均匀分布的回零误差，每个区间内分别实现回零操作1 000次。表1为针对给定的支腿回零误差下并联机构末端位置分布球半径及球内点占的百分比。以工况3为例，当每个支腿存在±0.07 mm均匀分布的回零误差时，并联机构末端位置有90.3% 的点落在半径为0.225 mm 的球内，相对应地并联机构的零点在空间的分布如图9所示。

表1 回零重复精度

图9 工况 3 零点位置分布

3.3 实际测量实验

为了测量NSRT副面并联机构的运动精度，利用Leica激光跟踪仪测量NSRT副面的运动轨迹。如图10所示，将角反射镜(靶球)放置于副面，激光跟踪仪安置于馈源仓顶部。已知NSRT副面与馈源仓顶部的距离约为7 m，且仪器精度5 μm +5 ppm，测量精度约为0.05 mm。

为了测量并联机构的回零精度，进行了23次回零操作，并记录了零点坐标。结果如图11所示，零点位置重复精度约为0.29 mm，90%的零点在半径为0.2 mm的球体内离散分布，分布呈现无规律特征。

图10 NSRT副面定位精度实测实验

图11 实测零点位置分布

为了测量并联机构的重复定位精度，使并联机构沿着某一坐标轴的方向来回运行。首先，使并联机构沿z轴方向运行，从零点开始以10 mm 的步进长度运动到+50 mm处；其次，再从+50 mm处运动到-50 mm处；最后，再从-50 mm回到零点位置。x、y坐标方向对应误差结果如图12所示。可以发现沿z轴方向运行时，x、y方向都有不同程度的偏移，且行程越长偏差越大。

同样使并联机构分别沿x、y方向运行，从零点开始以10 mm步长分别从原点运动到+40 mm处，再从+40 mm处分别运动到-40 mm处，最后从-40 mm回到零位置。图13为并联机构沿x轴方向运动时z、y坐标方向对应误差，受环境因素的影响，数据出现抖动，但不影响整体趋势。图14为并联机构沿y轴方向运动时x、z坐标方向对应误差。可以发现单坐标方向运行时，其他两个坐标方向有不同程度的偏移，且行程越长偏差越大。

图12 沿 z 轴方向运动时 x、y 坐标方向对应误差

图13 沿x轴方向运动时 z、y 坐标方向对应误差

最后测量并联机构实际工作位置的定位精度，使并联机构分别运行至四个波段对应位置，每个位置点重复运行5次(每次先执行回零操作再分别运行到四个波段对应的位置)，测量每个点对应的坐标。测量结果如图15所示，各点离散分布，重复精度平均偏差为0.26 mm。

图14 沿 y 轴方向运动时 x、z 坐标方向对应误差

图15 四波段重复定位精度

3.4 结果分析

几何误差模拟结果显示，如果保证杆长误差小于0.08 mm，铰链误差小于0.05 mm，则并联机构精度保持在要求范围内。

回零精度实测结果显示，零点位置重复精度约为0.29 mm，远大于0.07 mm的设计指标，90%的零点在半径为0.2 mm的球体内离散分布，分布呈现无规律特征。导致并联机构在其他运动过程中因基准不对而造成偏差。分别对影响零点位置重复精度的各个因素进行分析并确定主要误差源。

并联机构末端姿态为零时工作空间内同一z截面上，铰链间隙对位置精度影响基本相同[25]。本例中，在进行反复回零操作时终端姿态为零且在同一z截面上，因此铰链间隙误差不影响重复精度。铰链中心位置偏差对同一末端位姿精度影响相同。因此，可以排除铰链误差的影响。

在反复进行回零操作时，理论上杆长无变化，因此可以忽略滚珠螺旋副的传动误差，而驱动杆的加工误差及杆件受力变形误差在零点位置造成的误差是确定值，不会影响重复精度。因此，可以排除杆长误差的影响。

NSRT副面并联机构支腿的两个极限位置装有限位开关，支腿的零点是以限位开关为基准的相对位置。因并联机构的回零检测装置主要由增量式编码器与限位开关组成，执行回零操作时，限位开关反馈信号的异常，会造成并联机构的回零误差，从而影响零点位置的重复精度。

综上，可以确定影响并联机构零点位置重复精度的主要因素是回零误差。由表1所示仿真结果可知，当每个支腿存在±0.06 mm内均匀分布的回零误差时，并联机构末端位置落在半径为0.192 mm 的球体内；存在±0.07 mm内均匀分布的回零误差时，并联机构末端位置落在半径为0.225 mm的球体内。因此，NSRT副面并联机构的支腿可能存在±0.06～±0.07 mm的回零误差，使并联机构零点在半径为0.2 mm的球体内离散分布。

重复定位精度实测结果显示，单坐标方向运行时，其他两个坐标方向有不同程度的偏移，且行程越长偏差越大。由于并联机构的结构特性，动平台上x、y、z轴之间存在耦合关系。因此，单坐标方向运行时，除该测量轴以外的两个坐标轴方向上均存在耦合误差。此外，结构参数误差及螺距累积误差等因素会使得并联机构出现行程越长偏差越大的现象。

NSRT进行四个波段观测时并联机构对应重复位置精度偏差平均为0.26 mm。由于每次运行到4个波段对应位置前进行回零操作，而回零操作为后续的工作提供一个基准点，回零误差会引起这个基准点的偏移从而造成后续所有的工作点的偏差。综合分析，回零误差是造成并联机构工作偏差的主要原因。

4 结 论

1) 通过对几何误差进行模拟，得出为使并联机构精度保持在要求范围内，杆长误差应小于0.08 mm， 铰链误差应小于0.05 mm。

2) 通过分析比较实测结果与仿真结果，得出影响并联机构末端位姿精度的主要误差源是回零误差，支腿可能存在±0.06～±0.07 mm的回零误差。

3) 通过本文的实际测量与仿真分析可知，对射电望远镜这种高精度设备，以增量式编码器与限位开关相结合作为回零检测装置和反馈模块，长期工作后易造成并联机构运动精度下降的问题。

4) 设计高精度并联机构时应避免使用增量式编码器与限位开关相结合的回零检测装置和反馈模块，或者设计高精度的回零方式及回零控制策略。NSRT副面并联机构后续误差补偿工作将主要针对回零误差进行，具体为将增量式反馈元件换成绝对位置反馈元件，采用绝对位置控制方式。