箱梁截面有效宽度对等截面连续梁桥的受力影响分析
孙 东
(安徽省交通勘察设计院有限公司,安徽 合肥 230011)
0 引 言
预应力混凝土等截面连续箱梁桥具有外形美观、整体性好、横向抗扭刚度大等优点,因此在桥梁设计中得到广泛的应用,但是在桥梁设计中往往忽略了剪力滞对桥梁结构受力分析的影响,导致桥梁部分构件应力过分集中造成桥梁的失稳和局部破坏,给工程建设带来巨大的损失和灾难。
箱型截面梁受对称垂直力作用时,受压翼缘上的压应力随着离腹板距离增加而减小,这种现象称为剪力滞后或剪力滞效应。实验成果和理论分析都证实,宽翼缘箱型截面梁存在剪力滞现象,忽略剪力滞效应的影响,就会低估箱梁腹板和翼板交接处的应力集中,因此在桥梁设计中必须考虑剪力滞对结构受力分析的影响。如果按照精确的剪力滞计算公式或空间有限元来分析截面的应力是非常复杂的,因此本文采用偏安全的简化计算方法,引入箱型截面梁翼缘有效宽度,通过工程实例和桥梁博士软件,分析箱型截面梁翼缘有效宽度对主梁结构计算结果的影响。
1 项目概况
主桥桥跨布置为(30+45+30) m,上部构造采用等截面预应力混凝土连续箱梁,单箱单室,直腹板,顶板宽度为8.0 m,底板宽度为5 m,翼缘宽度为1.5 m,梁高2.7 m。跨中处箱梁顶板厚25 cm,底板厚28cm,腹板厚50 cm,顶板、底板、腹板在端横梁和中横梁处设置5 m渐变段。箱梁采用一次落架现浇施工。
2 主要计算参数选取及计算荷载
2.1 主要计算参数选取
(1)混凝土。C50混凝土,fck=32.4 MPa,ftk=2.65 MPa,fcd=1.83 MPa,E=3.45×104MPa;C50混凝土容重γ=26 kN/m3;沥青混凝土容重γ=24 kN/m3。
(2)钢绞线。fpk=1 860 MPa,Ep=1.95×105MPa,预应力筋张拉控制应力σcon=0.72fpk=1 339 MPa,管道每米局部偏差对摩擦的影响系数k=0.001 5,预应力钢筋与管道壁的摩擦系数μ=0.17,钢束锚固时弹性回缩变形量对于单端张拉预应力筋为6 mm,对于双端张拉预应力筋为12 mm。
(3)热膨胀系数。混凝土热膨胀系数采用α=1.1×105。
(4)收缩徐变时间:3 650 d。
(5)结构重要性系数:1.1。
2.2 计算荷载
(1)恒载:一期恒载包括主梁自重、横隔梁重量,横隔梁按集中荷载计算;二期恒载包括桥面铺装、护栏等。
(2)活载:公路-I级;
(3)整体温度:系统整体升温25℃,降温20 ℃。
(4) 梯度温度:根据《公路桥涵设计通用规范》(JTG D60-2015)竖向温度梯度曲线取值。正温差T1=14℃,T2=5.5℃,竖向日照反温差为正温差乘以-0.5。
(5)不均匀沉降桥墩0.01 m、桥台0.007 m。
3 计算模型
全桥共划分为131个单元,132个节点。其中2#、40#、93#和131#节点为支承节点,主梁全部采用梁单元进行模拟,主梁按A类预应力混凝土构件设计,全桥计算模型如图1所示。

图1 计算模型
4 计算结果分析
4.1 箱梁翼缘有效宽度计算
为了分析箱梁截面有效宽度对桥梁结构计算结果的影响,分别取边支点、中支点、边跨及中跨特征位置,根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018)第4.3.4条,得到箱梁截面上、下缘有效宽度数值,见表1。

表1 有效宽度计算结果表
根据表1计算结果,原截面顶宽8.0 m,底宽5.0 m,边支点位置截面有效宽度比原截面宽度折减了约15%,中支点位置截面有效宽度比原截面宽度折减了约30%,将折减后箱梁截面有效宽度值输入桥梁博士软件中进行计算。
4.2 持久状况承载能力极限状态验算
根据表2计算结果,基本组合下,考虑和未考虑截面有效宽度计算的两种抗弯极限承载力,抗力值最大相差约5%。
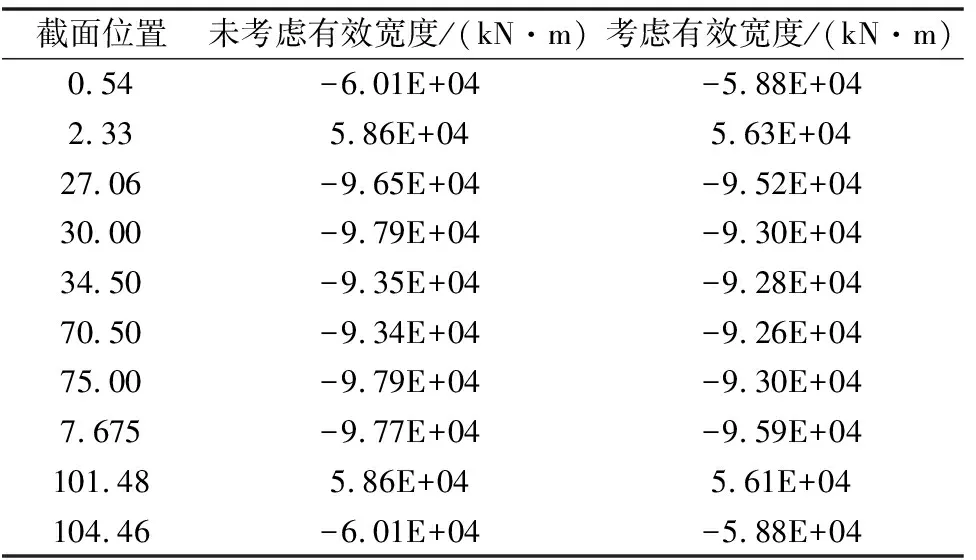
表2 基本组合下主梁抗弯承载力
4.3 持久状况正常使用极限状态验算
根据表3计算结果,频遇组合下,考虑和未考虑截面有效宽度计算截面上、下缘最小正应力,中支点处最小正应力差值最大为1.23 MPa,端支点处最小正应力差值最大为0.19 MPa,跨中处最小正应力差值最大为0.21 MPa。

表3 频遇组合下主梁上、下缘最小正应力
根据表4计算结果,准永久组合下,考虑和未考虑截面有效宽度计算截面上、下缘最小正应力,中支点处最小正应力差值最大为0.65 MPa,端支点处最小正应力差值最大为0.19 MPa,跨中处最小正应力差值最大为0.11 MPa。

表4 准永久组合下主梁上、下缘最小正应力
根据表5计算结果,标准组合下,考虑和未考虑截面有效宽度计算截面上、下缘最大正应力,中支点处最大正应力差值最大为1.99 MPa,端支点处最大正应力差值最大为0.22 MPa,跨中处最大正应力差值最大为0.37 MPa。

表5 标准组合下主梁上、下缘最大正应力
5 结 论
通过以上计算结果对比分析,截面有效宽度对主梁极限承载能力影响很小,但对应力的影响,特别是标准组合和频遇组合下主梁的最大、最小正应力计算结果影响较大,因此在预应力混凝土等截面连续箱梁设计中必须考虑截面有效宽度对结构受力分析的影响。

