寿春西路桥参数振动分析

杨吉新， 丁 宇， 吴爱平， 张 朝， 余 飞

(武汉理工大学，湖北 武汉 430061)

0 引 言

众所周知,对于斜拉桥来说,斜拉索是其重要的受力构件。斜拉索可能在微小的外激励下诱发高幅度振动,是因为其质量轻、柔度大及阻尼小等特点[1]。然而大幅度振动会对损害桥梁结构的安全性能,对其使用寿命也会造成一定影响。在已有的文献中大部分学者认为,斜拉索发生参数振动的概率与梁体振动激励频率有关,当拉索的固有频率在梁体自振频率附近的区间时,拉索有很大概率会产生幅度很大的动力响应,此时发生的参数振动被称为主共振;当2倍的拉索固有频率处于梁体自振频率的、附近区间时,拉索也会激发大振幅的动力响应,称为参数主共振。[2]由此可见,并不是所有拉索都会发生参数振动,拉索能否发生参数共振与其桥的动力特性密切相关,特别是其固有频率与全桥竖向振动频率是否匹配。就实际工程而言,构建全桥的振动数值计算模型来分析索结构参数振动的发生概率比较复杂,本文采用多重RITZ向量法对全桥整体振动频率与模态进行分析。

1 工程背景简介

寿春西路桥位于安徽省六安市裕安区，包括两侧桥台在内全长共845m，跨径布置为3.5m(桥台)+3×30m(先简支后连续组合箱梁)+3×30m(先简支后连续组合箱梁)+4×30m(先简支后连续组合箱梁)+(108+70)m(混合梁斜拉桥)+4×30m(先简支后连续组合箱梁)+4×30m(先简支后连续组合箱梁)+4×30m(先简支后连续组合箱梁)+3.5m(桥台)。主梁采用钢-混凝土混合梁，大悬臂展翅箱型截面是其截面形式；寿春西路桥的主塔为无背索斜塔，大幅增加了副塔刚度，改善了副塔受力，减小了变形。斜拉索效率因其布置方式得到充分发挥，同时，对横向倾角较大而又无横梁的副塔增大了轴向力，降低了横向弯矩产生的开裂风险。塔柱为矩形塔，主塔上塔柱高70m，副塔上塔柱高50m，下塔柱高约18.5m。从顺桥向看塔柱呈“V”形，从横桥向看塔柱呈“Λ”形，8 对斜拉索对称布置于主跨与边跨。桥型布置图如图1所示。

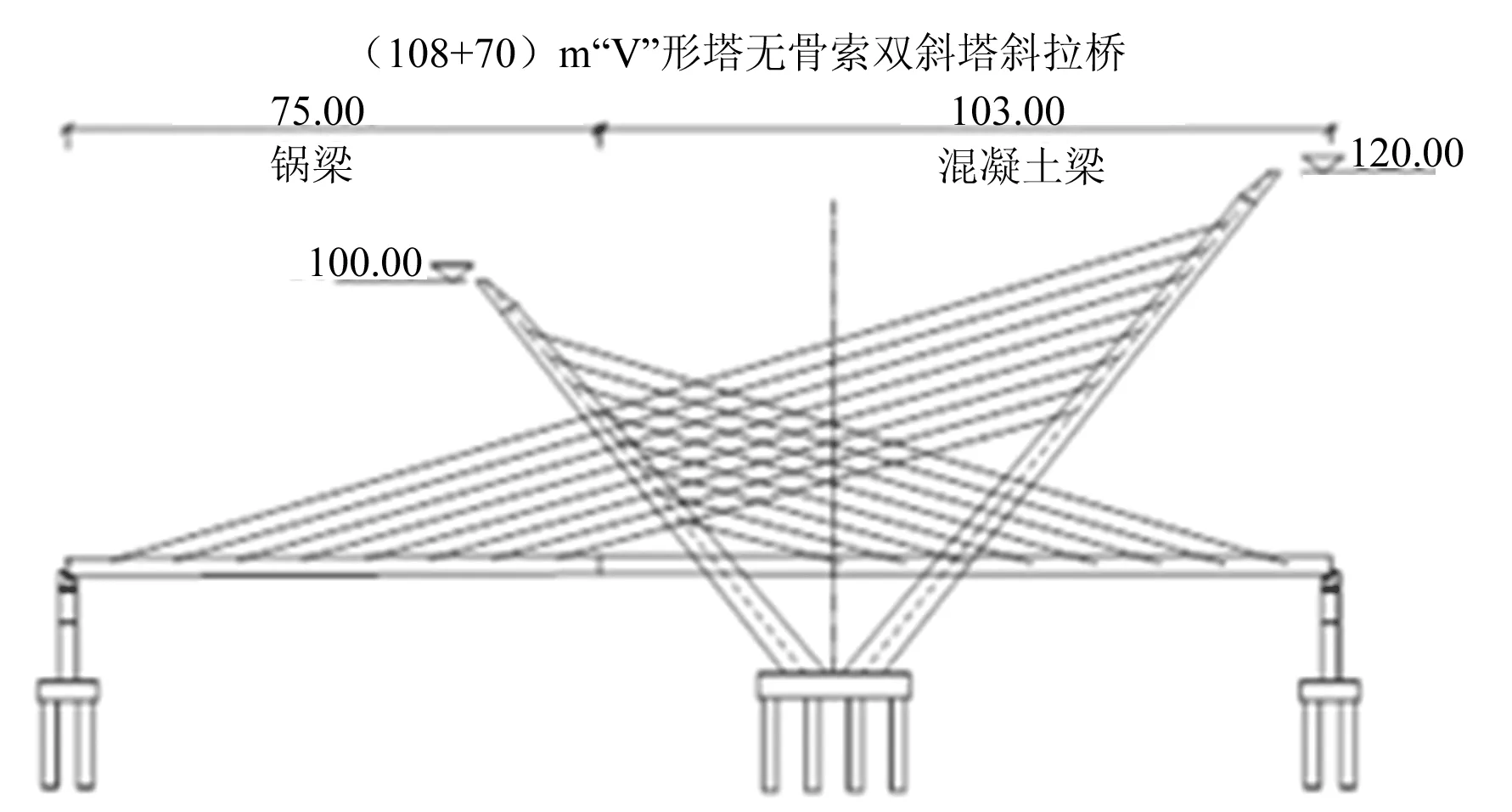
图1 寿春西路桥布置图

全桥设置24对共48根斜拉索,分别为M1～M8、S1～S8、B1～B8,其中连接主塔与副塔的是M索,使用的是15.2-12型钢绞线,锚固于副塔,于主塔顶进行张拉,又被称为“塔间索”;连接副塔与钢梁的是S索,使用的是15.2-19 型钢绞线,锚固于钢梁,于副塔顶进行张拉;连接副塔与混凝土梁的为B索,使用的是15.2-19 钢绞线,锚固于混凝土梁,于副塔顶进行张拉。

2 建立参数振动模型

2.1 振动系统的建立

塔索梁耦合振动模型如图2所示,振动系统由桥塔、斜拉索、梁三个部分组成。在建立振动模型时,将所有因素和条件都列入考虑往往难以实现并且也不合理,为了能够切实反映斜拉索的振动特性,需要做出以下假设[3]:

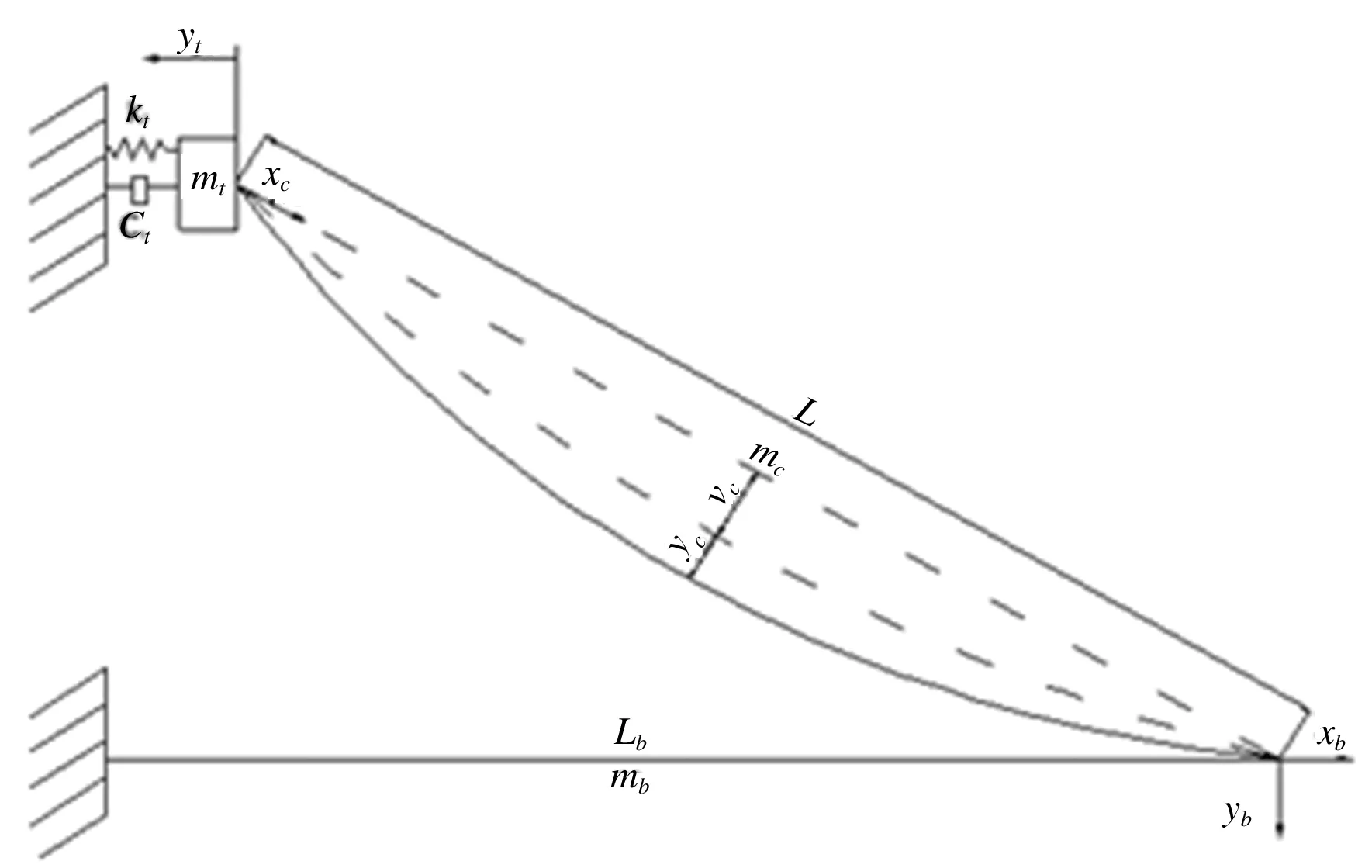
图2 振动模型

(1)只考虑拉索的抗拉刚度;

(2)拉索的重力垂度曲线为抛物线;

(3)拉索受力均匀,变形服从虎克定律;

(4)只考虑拉索平面内振动。

图2中主要参数定义为:mc为拉索线密度，kg/m;Lb为梁悬臂长度;L表示拉索上下端直线距离;mb为主梁线密度，kg/m;yc为动位移,表示拉索偏离垂度曲线的距离;v0为垂度作用下拉索偏离原位置的距离;mt为副塔质量，kg;kt为副塔侧向刚度。

2.2 拉索振动方程的建立

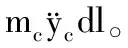
(1)

初始张力T和动张力Td组成T,当静力平衡时,Td=0,yc=0,拉索的动张力可得:

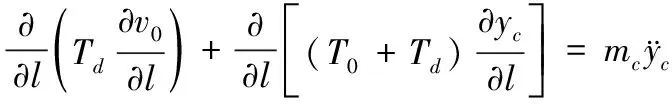
(2)

由拉索除端部约束外没有其他外荷载[4]，得:

(3)

式中:H为拉索的静态轴向拉力。

联立方程得:

(4)

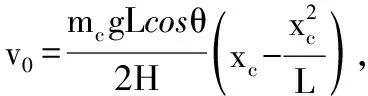
由基本假定1得,yc可表示为:yc(xc,t)=Yi(t)φi(xc)。式中:Yi(t)为拉索振型;φi(xc)为第i阶振型。分析Tagata[5]的研究,本文只考虑拉索的一阶振型:

φi(xc)=sin(πxc/L)

(5)

考虑模型的边界条件:yc(0,t)=Ytsinθ,yc(L,t)=Ybcosθ则:

(6)

拉索的动应力Td可表示为:

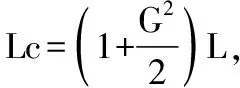
为便于数值求解,运用Galerkin法,在区间[0,L]内进行积分[6],求解后化简得拉索振动的常微分方程如下:

A15Yb+A16Yt=0

(8)

各项系数如下:

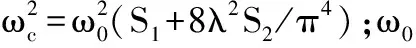
2.3 钢梁振动方程的建立

根据达朗贝尔原理得,混凝土梁的振动方程为:

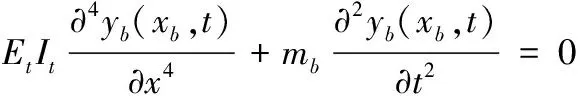
(9)

式中:EtIt为梁的弯曲刚度;mb为梁的线密度。

分离变量后得到:

yb(xb,t)=φ(xb)Yb(xb)

(10)

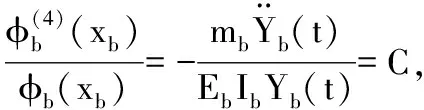
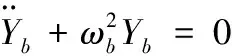
(11)

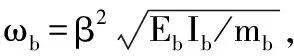
2.4 副塔振动方程的建立

根据达朗贝尔原理得,副塔的动力平衡方程为:

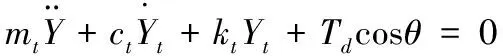
(12)

式中:mt为弹簧块质量；ct为桥塔结构阻尼；kt为桥塔侧向刚度。

将式(7)代入式(12)可得:

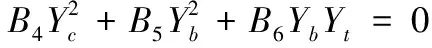
(13)

式中各项系数如下:

式中:ηt为桥塔质量块阻尼,ηt=2ξtωtξt为桥塔质量块阻尼比;ωt为桥塔质量快的固有频率,ωt=(ktLc+EA)/mtLc。

将拉索振动方程、钢梁振动方程、副塔振动方程联立得:

(14)

3 参数振动可能性分析

3.1 全桥模态分析

运用建模软件MIDAS-Civil建立寿春西路桥成桥状态模型,分析比较多种有限元动力分析方法后,最终采用多重Ritz向量法求出全桥前十阶竖向振动模态,与拉索固有频率相比较,列出所有可能发生参数振动的拉索。全桥竖向振动模态分析结果见表1。

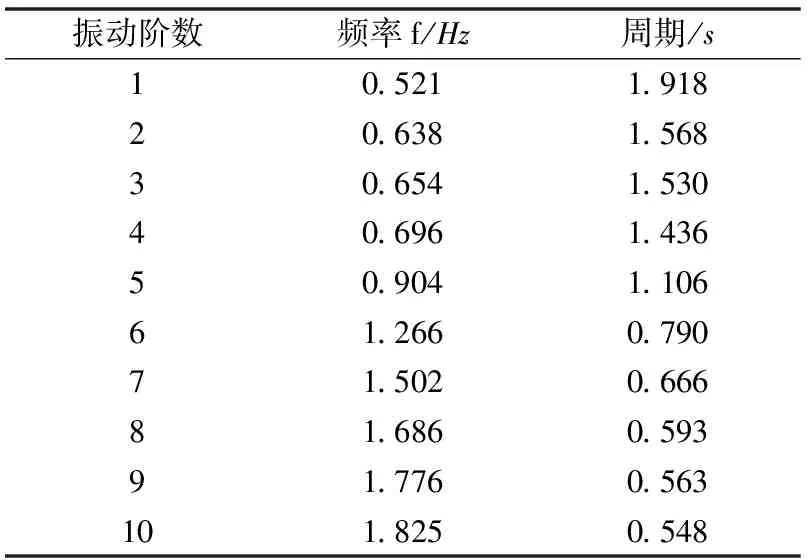
表1 全桥竖向振动模态表

3.2 斜拉索基频计算

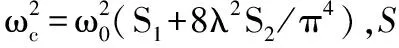
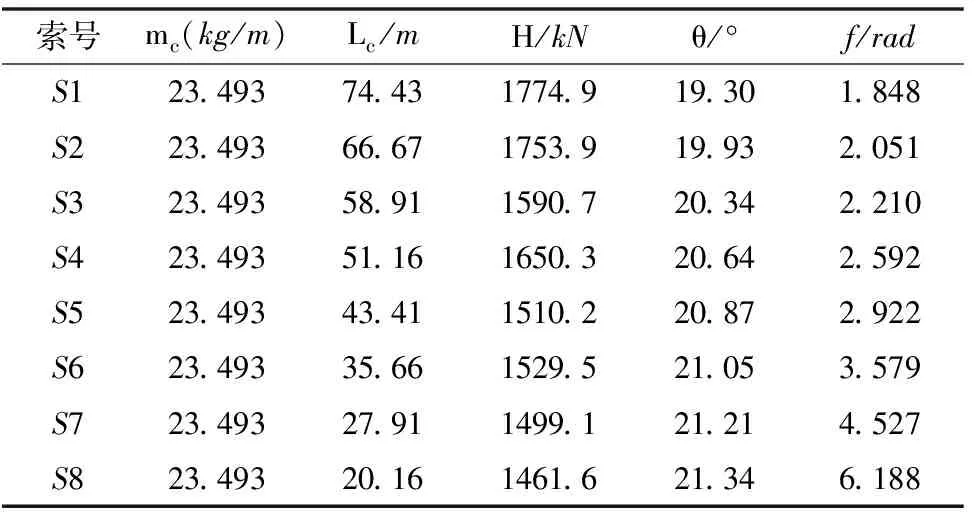
表2 拉索参数表

3.3 拉索基频与全桥振动频率的关系

当拉索固有频率落在全桥的振动频率±5%的区间时[1],斜拉索有很大概率发生大幅度的动力响应,此时的参数振动被称为主共振;当拉索固有频率的2倍落在全桥的振动频率±5%的区间时,拉索也有较大概率诱生大幅度的动力响应,而此时的参数振动称为主参数共振。对比表1和表2可知,容易发生主共振的拉索有S1、S2、S4、S7、S8;全部S索都易发生主参数共振。

4 数值计算及分析

4.1 参数振动特性

由于非线性高阶常微分方程组的复杂与烦琐,本文采用自适应龙格-库塔算法编程求解式(14)。通过有限元软件算得钢梁和副塔的参数如下:

钢梁线密度Mb=8.9×105kg/m;

弹性模量Eb=3.45×1010Pa;

惯性距Ib=4.4×103m4;

副塔质量mt=5.76×106kg。

拉索上端对应副塔刚度,通过施加单位荷载求其位移的倒数算得，计算结果见表3。

表3 副塔刚度表

在无阻尼的情况下能更好地反映拉索的参数振动特性,取初始变量Yt=0.001m,Yc=0.001m,Yb=0.001m,求解S6、S7、S8索的参数振动时程曲线。计算结果如图3所示，图3a、图3b分别表示拉索S7前500s、前150s主共振的时程曲线，图3c、图3d表示拉索S8前500s、150s主共振的时程曲线,图3e表示S6前500s主参数共振时程曲线,图3f表示S6前500s主共振时程曲线。

图3 时程曲线图

4.2 结果分析

由图3可知,在只有0.001m的小振幅激励下,S7、S8发生了大幅度的主共振,最大振幅达到0.18m左右,前500s时程曲线图可以看出,S7、S8都体现出了明显的“拍”的现象,这一非线性现象与理论相符[7]。对比S7、与S8可发现,在前500s时程曲线中,S7完成了大约7.5个“拍”,而S8完成了大约12.5个“拍”,且S8的振幅要略小于S7的振幅。将单位时间内完成“拍”的次数定义为“拍”的频率,那么不难看出,在初始条件都相同的情况下,如果“拍”的频率越大,那么其振幅就越小。

观察图3e、图3f可以看出,拉索S6发生了主参数共振,但S6并没有发生主共振,其振幅很小。该结果表明,它们诱发的条件是相对独立的。观察拉索主共振和主参数共振的振幅发现,在初始条件相同的情况下,主参数共振的振幅比主参数振动的振幅要小一些。在相同条件下,拉索S7发生主共振时,在500s内完成7.5个“拍”,而发生主参数共振是仅完成2个“拍”,说明主共振更容易发生。

5 结 论

本文以寿春西路桥为背景,建立塔索梁非线性耦合振动模型,为了切实反映拉索的振动性,考虑了拉索垂度效应、副塔的刚度以及拉索的倾角等因素。运用自适应龙格-库塔算法求解振动微分方程,运用MATLAB分析拉索振动时程曲线图,得出以下结论:

(1)微小的激励在特定条件下可诱发拉索发生大幅度参数振动,并有“拍”的现象伴随出现。

(2)在相同的初始条件下,拉索发生参数振动,如果振动的“拍”越大,那么其振幅就越小。

(3)导致拉索发生主共振和主参数共振的条件是相对独立的。

(4)在相同的初始条件下,主参数振动振幅往往要比主共振的振幅要小一些。

(5)在相同的初始条件下,主共振要比主参数共振更容易诱发。