中承式钢箱提篮拱桥在不同软件分析下的结果对比

胡良红， 黄飞鸿， 刘 信

(1.中国华西工程设计建设有限公司安徽分公司，安徽，合肥 230032；2.合肥工业大学 土木与水利工程学院，安徽，合肥 230009；3.安徽省交通规划设计研究院，安徽，合肥 230088)

0 引 言

随着科技的进步，有限元分析软件越来越多，而不同的学者和研究人员学习和使用的软件也各不相同，然而对于同一问题，可以采用多种有限元软件进行分析。例如分析桥梁受力特征，可以采用桥梁博士、MIDAS Civil、ANSYS等；分析结构的地震响应，可以采用ANSYS、ABAQUS、OpenSees等；分析岩土结构的受力特性，可以参与FLAC3D、MIDAS Gen等。为比较不同有限元软件分析同一问题之间的差异，本文以某座中承式钢箱提篮拱桥为背景，采用ANSYS和MIDAS Civil分别建模，从模型输入、静力响应和动力特征参数三方面进行比较分析。

1 有限元模型建立

1.1 工程概况

背景桥梁主桥采用跨度为120 m的中承式钢箱提篮拱桥[1]，受力模式属于拱梁组合体系结构[2]，主桥拱圈为双肋单箱单室变截面钢箱拱，拱轴线在拱肋平面内为二次抛物线，矢跨比为1∶3，矢高为40 m，如图1所示。主拱肋竖向与水平面的夹角为75°，内倾角为15°。两拱肋之间用3道钢箱横撑连为一个整体。主拱肋分为钢箱拱肋和实心矩形预应力混凝土两部分，尺寸由1.5 m×2.0 m渐变为3.5 m×4.5 m。桥梁主跨桥面系采用正交异性钢桥面板[3]结构形式。桥面板厚度为16 mm，横桥向用高强螺栓与钢纵梁进行栓接。桥面板由4根I型小纵梁进行支撑，小纵梁之间再设置U型加劲肋，横梁采用工字型，纵桥向间距为3 m，吊杆与钢梁的锚固结构为全焊结构。吊杆采用Φ15-15及Φ15-27钢绞线。本桥共设14对吊杆，沿桥轴方向吊点标准中心距为6.0 m。主桥两侧的人行辅桥分为两部分，第一部分采用开口截面，与主桥相连。第二部分为钢箱截面，立面采用1.7次抛物线，平面为圆弧线。主拱座采用承台接群桩基础。吊杆编号如图2所示。

图1 桥梁总体布置图

图2 吊杆编号

1.2 ANSYS有限元模型建立

车行桥和人行桥的拱肋、横撑、挑梁均为带有纵向加劲肋的钢箱梁，其中拱肋为变截面钢箱梁，截面构造较为复杂，故选用软件中支持自定义截面类型的Beam 188单元进行模拟，每个节点有3个自由度，可用于弹塑性分析，支持自定义截面[4]。纵横梁亦采用该单元类型，截面均为在CAD中绘制后导入ANSYS中。吊杆采用Link180单元，该单元支持大变形、大应变，可输入初应力，且设置为仅受拉，非常适合模拟索结构。全桥共离散梁单元1 256个，杆单元28个，如图3所示。

图3 桥梁ANSYS有限元模型

桥梁的边界条件按照设计图纸要求进行约束，承台底部固结，拱肋与承台连接及桥面板约束条件如图4所示。

图4 桥梁边界条件布置图

1.3 MIDAS Civil有限元模型建立

MIDAS Civil有限元模型中拱肋、横撑、挑梁、桥面系纵梁及横梁均采用梁单元进行模拟，均使用SPC[5]自定义截面功能导入；吊杆采用只受拉桁架单元进行模拟。荷载取值及边界条件设置与ANSYS模型中保持一致。全桥同样共离散梁单元1 256个，杆单元28个，如图5所示。

图5 桥梁MIDAS Civil有限元模型

2 比较分析

2.1 模型输入条件对比

两种模型中的截面均是由CAD导入，ANSYS中使用的是Beam 188单元的自定义截面功能，MIDAS Civil中使用的是SPC自定义截面功能，两种方法的导入精度会有所不同。本文选取拱肋跨中位置截面、拱脚位置截面、纵梁截面、横梁截面，将两种模型计算的截面特性值与使用材料力学方法计算的截面特性值进行对比[6]，结果见表1。

表1 截面特性值对比表

由表1可知，ANSYS与MIDAS Civil软件计算出来的截面特性值与采用材料力学方法计算出来的截面特性值都非常接近，误差均小于1%，因此，可以认为在截面导入方面，两种有限元软件之间并无明显差异。

2.2 静力计算结果对比

静力计算通常可以用来验证结构的强度、刚度和稳定性，是工程计算中基础的工作，本文静力计算不做移动荷载分析，成桥后将活载以车道荷载形式加到桥面系上，视为恒载处理，故该部分只计算恒载作用下桥梁结构的受力响应。

本文计算了拱肋1/2、拱脚位置、纵梁1/2及横梁1/2位置处应力，因结构是对称的，仅列出左侧计算结果，见表2。吊杆是中承式提篮拱桥的重要构件，其安全与否决定了整个结构的安全性能，故对吊杆内力进行计算是非常有必要的，两种软件吊杆内力的计算结果如图6所示。

表2 静力计算结果表

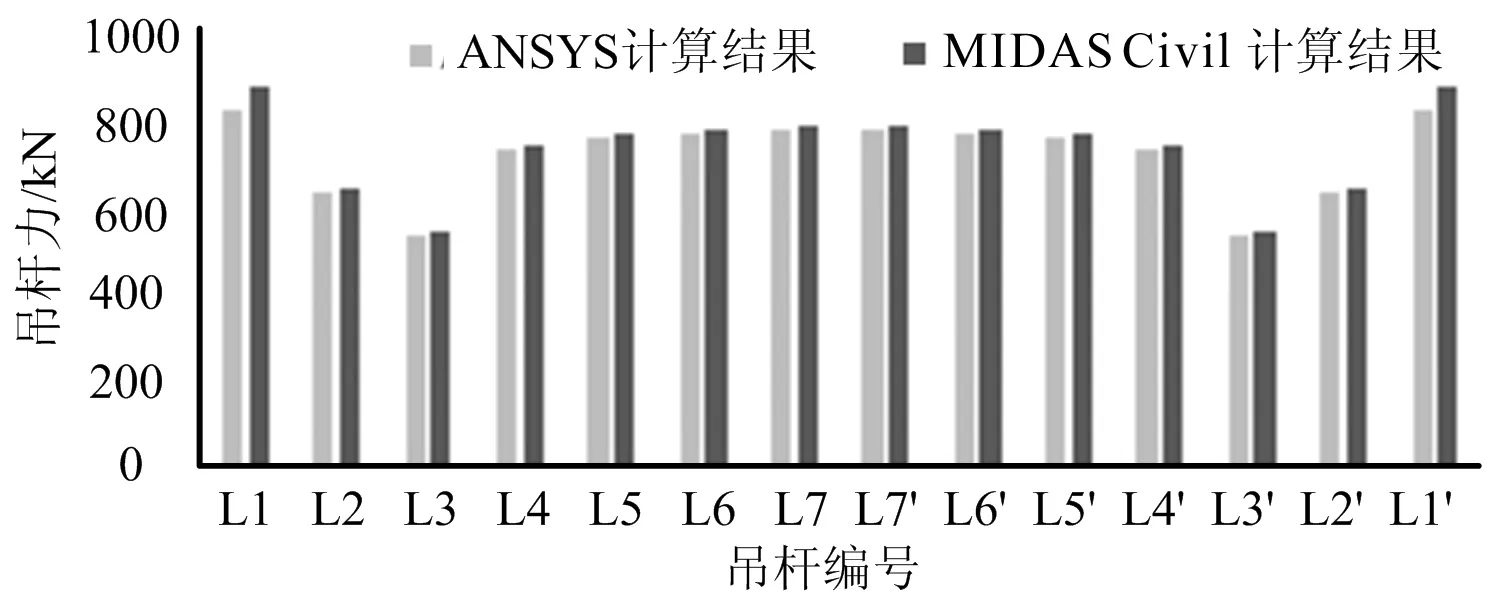
图6 吊杆内力计算结果图

由表2可知，ANSYS应力计算结果与MIDAS Civil计算结果基本一致；图6显示了两种模型计算的吊杆内力基本一致，跨中位置几根长吊杆仅相差7 kN；而两侧的短吊杆虽然差值最大达到49 kN，但也只相对差4.72%，仍在可接受范围之内，因此可认为采用相同的荷载和边界条件，两种软件的计算结果并无明显差异。

2.3 动力特性计算结果对比

桥梁的动力特性是衡量结构整体刚度及使用性能的重要指标之一，结构固有频率和振型是最基本的动力特性参数，模态分析[7]是一种典型的线性分析方法，是开展其他动力学分析的基础性工作[8]。使用ANSYS模态分析模块与MIDAS Civil特征值分析功能，分别对背景桥梁进行动力特性计算，求解桥梁固有频率及前三阶振型，计算结果见表3。

表3 桥梁动力特性计算结果表

由表3可知，两种模型计算的桥梁结构固有频率及自振周期基本一致，振型特征是完全吻合的，说明了两种模型的整体刚度是基本一致的。前三阶的振动主要是拱肋的振动，第一、二阶均为拱肋在横桥向的振动，第三阶则为拱肋在顺桥向的振动，周期衰减。

3 结 论

本章依托某中承式钢箱提篮拱桥为工程背景，使用有限元分析软件ANSYS及MIDAS Civil分别建立了有限元模型，来探讨不同有限元分析软件分析同一工程实例之间的差异，分析可得以下结论：

(1) 模型输入条件方面，在控制材料参数与设计要求保持一致的前提下，两种有限元软件计算的截面特性基本一致，且与力学理论计算值很接近。

(2) 静力响应方面，采用相同的荷载和边界条件，两种软件的计算结果并无明显差异。

(3) 动力特性参数方面，两种软件计算的桥梁结构固有频率及自振周期基本一致，说明了两种模型的整体刚度基本一致。

说明只要保持材料输入、边界约束、荷载取值等设计参数一致，且建模过程并无错误，采用不同的有限元软件分析同一工程问题，其计算结果是基本一致的，但不同有限元软件有不同的侧重点和优势，应根据工程需要灵活选用。