基于SC分集的混合FSO/RF航空通信系统性能分析
刘文亚,赵尚弘,王 翔,牟 迪
(空军工程大学信息与导航学院,陕西 西安 710077)
1 引 言
在无线通信中,自由空间光(FSO)通信具有宽带宽、频谱充裕、抗干扰能力强、天线尺寸小及部署成本低的优点而备受关注,在未来航空信息组网方面有广阔的应用前景[1-2]。然而,FSO通信易受云雾及沙尘暴等恶劣天气影响,即使在晴朗的天气下,也容易受大气湍流的影响[3]。射频通信链路主要受雨衰的影响,对云雾、沙尘暴及大气湍流等因素不敏感[4]。因此,综合考虑环境对FSO及RF信道的不同影响,通过并行传输的链路部署来减轻信道的衰落影响,从而实现高速、可靠、稳定的混合FSO/RF航空通信系统。
目前,针对混合并行FSO/RF通信系统的研究主要聚焦在硬切换及软切换两个方面。其中,硬切换方面大多研究基于信噪比阈值进行链路切换的方案[5-7]。软切换方面大多研究信道编码、调制及数据划分方案[8-10]。然而,无论是基于信噪比阈值的FSO/RF硬切换方案,还是通过编码、调制进行数据划分的软切换方案,系统在发射端必须要接收到可靠的信道状态信息(CSI),这增加了一条反馈链路的需求,提高了系统设计及实现的复杂性。文献[11]中提出了基于选择合并(SC)分集的混合FSO/RF通信系统。射频和激光链路上传输相同的数据,在接收端采用SC分集技术,利用了并行的RF链路来降低大气湍流对FSO通信的影响,发射端不需要获取CSI,也不需要考虑编码以及链路切换方案,简化了系统设计。在文献[11]中考虑射频链路信道为瑞丽信道模型,FSO大气湍流信道为Gamma-Gamma信道模型。文献[12]对其进行了进一步分析,其中RF链路服从Nakagmi-m信道模型,该模型对实测数据具有很好的拟合性,FSO大气湍流信道仍为Gamma-Gamma信道模型。Gamma-Gamma分布可用于表征中到强湍流中的光强起伏,但不适用于孔径平均效应下的自由空间光通信,孔径平均效应可有效抑制大气湍流对自由空间光通信的影响。Barrios R和Dios F提出了适用于弱到强湍流及平均孔径条件下的Exponentiated Weibull分布模型[13-14],并通过实验验证了模型在平均孔径效应及各种湍流强度下的准确性。
本文研究了基于SC分集的混合FSO/RF航空通信系统性能。FSO链路采用Exponentiated Weibull分布模型,RF信道衰落服从Nakagami-m分布。利用Meijer′s G函数推导出混合FSO/RF航空通信系统中断概率及平均误码率闭合表达式,通过闭合表达式进行仿真,对比分析了不同湍流强度、调制方式及并行分集的通信方案对系统中断、误码性能的影响。
2 系统及信道模型
基于SC分集的混合FSO/RF航空通信系统模型如图1所示。在发射端系统采用M-PSK调制,调制信号输入到FSO和RF两个子系统同时传输,在接收端进行检测并运用选择合并分集技术进行处理。

图1 基于SC分集的混合FSO/RF通信系统Fig.1 Hybrid FSO/RF system based on selection combing diversity
2.1 FSO链路
在FSO子系统采用强度调制/直接检测(IM/DD),将直流偏压加到强度调制信号上,以避免调制信号的负值。然后,激光二极管通过FSO信道传输光信号。在FSO子系统的接收器处,光电探测器通过直接检测将入射信号转换为电信号,在FSO子系统接收端yFSO可以表示为:
yFSO=RIFSOx+nFSO
(1)
式中,IFSO为由大气湍流引起的信道衰落增益;x为M-PSK调制信号;R为光电转换效率;nFSO为加性高斯白噪声信号。
在FSO子系统接收端采用大孔径接收技术,考虑孔径平均效应,激光链路服从Exponentiated Weibull分布,则信噪比γFSO的概率分布函数(PDF)表示为[15]:

(2)
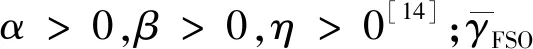
(3)
2.2 RF链路
在RF子系统发射端对信号进行上变频处理,载波选取频率为60 GHz的毫米波。在RF子系统接收端,RF信号通过下变频并解调成原始信号。RF接收端信号yRF可以表示为:
yRF=hRFx+nRF
(4)
其中,hRF代表信道的衰落因子;x为M-PSK调制信号;nRF为加性高斯白噪声信号。
RF链路服从Nakagami-m分布,信噪比的概率密度函数分布表达式为[16]:
(5)
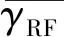
(6)
其中,γ(m,x)为不完全伽马函数。
2.3 基于SC分集的混合FSO/RF通信系统
SC分集是一种较为简单、直接的组合方案。在接收端测量每一条链路的电信噪比,并选择电信噪比最高的信号作为输出。因而,输出信号的信噪比为[12]:
γSC=max(γRF,γFSO)
(7)
因此,系统接受端瞬时信噪比的累积分布函数(CDF)为:
FγSC(γ)=FγRF(γ)FγFSO(γ)
(8)
将式(3)和式(6)代入式(8),可以得到接受瞬时端信噪比的CDF为:

(9)
3 系统性能分析
3.1 中断概率
对于通信系统来说,系统中断概率是衡量通信系统传输可靠性的重要指标之一,可表示为接受端信号的信噪比低于某个信噪比阈值的概率。因此,系统中断概率的数学表达式为:
Pout(γth)=P(γ<γth)=F(γth)
(10)
3.1.1 单FSO系统
仅采用一条激光链路进行通信时,系统中断概率的数学表达式为:
PFSO-out(γth)=P(γ<γth)=FγFSO(γth)
(11)
3.1.2 单RF系统
仅采用一条射频链路进行通信时,系统中断概率的数学表达式为:
PRF-out(γth)=P(γ<γth)=FγRF(γth)
(12)
3.1.3 基于SC分集的混合FSO/RF通信系统
对基于SC分集技术的并行FSO/RF通信系统来说,系统中断概率的表达式为:
Psc-out(γth)=P(γ<γth)=FγSC(γth)
(13)
3.2 平均误码率
平均误码率亦是评价系统性能的指标之一。根据接收端的瞬时信噪比及其概率密度函数,可推导出通信系统平均误码率的闭合表达式。
对于M-PSK调制,瞬时误码率的表达式可以写成[16]:

(14)
其中,erfc(·)为互补误差函数。
对上式进行求导,可得到瞬时误码率的一阶导数表达式:
(15)
系统的平均误码率为[16]:

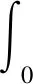
(16)
3.2.1 单FSO系统
对于仅用一条激光链路通信的FSO子系统,将(3)及式(15)代入式(16)中,根据广义二项式定理及Meijer′s G函数的运算性质[17-18],可得系统平均误码率表达式为:
(17)
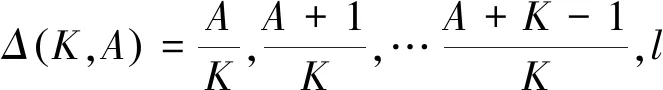
3.2.2 单RF系统
同理,将式(6)及式(15)代入式(16)中,利用Meijer′s G函数的运算性质[17-18],推导得到单RF通信系统的平均误码率表达式为:
(18)
3.2.3 基于SC分集的混合FSO/RF通信系统
将式(9)、(15)代入式(16)中,根据广义二项式定理及Meijer′s G函数的运算性质[17-18],推导得到SC分集下混合FSO/RF通信系统的平均误码率表达式为:
(19)

4 仿真结果分析
在本节中,根据上述推导得到的中断概率的闭合表达式(11)、(12)、(13)及平均误码率闭合表达式(17)、(18)、(19),分析了不同情景下混合FSO/RF航空通信系统性能,表1、表2和表3中列出了仿真参数。

表1 FSO系统参数Tab.1 FSO system parameters

表2 RF系统参数Tab.2 RF system parameters

图2为中断概率在不同湍流强度及通信方案下随平均信噪比变化规律图。大气湍流信道参数如表3所示。取RF链路衰落指数m=3,此时为RF链路为弱衰落,由图2可以看出随湍流强度增大,混合并行FSO/RF通信系统中断性能降低,如当平均信噪比为24 dB,弱湍流条件下系统中断概率为Pout=1.968×10-8,而强湍流强度条件下中断概率增大为1.004×10-5,增加了三个数量级。混合FSO/RF通信系统要比单一的FSO和单一的RF系统更加稳定,中断性能更好,如当强湍流情况下且链路平均信噪比为20dB时,混合FSO/RF通信系统的中断概率为Pout=3.99×10-4,而单FSO链路及单RF链路中断概率分别为1.11×10-1和3.59×10-3。

表3 信道湍流参数Tab.3 Channel turbulence parameters
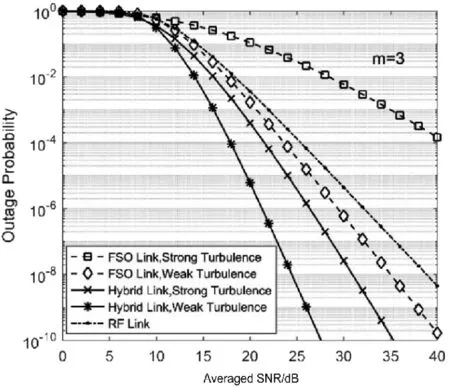
图2 不同通信系统及湍流强度条件下中断概率变化规律Fig.2 OP performance comparison of the hybrid FSO/RF,RF-only and FSO-only systems under various turbulence conditions
混合FSO/RF通信系统采用BPSK调制,不同衰落指数和大气湍流强度条件下系统平均误码率性能随信噪比变化规律如图3所示。数值仿真选取表1、表2及表3参数。仿真结果表明,随着湍流强度增大及m的减小及RF信道衰减程度增强,系统平均误码率不断增大,如平均信噪比为15 dB时,弱湍流及RF弱衰减(m=3)时,系统误码率为1.719×10-6,强湍流及RF强衰减(m=1)时,系统误码率增加为5.893×10-4,增加了两个数量级。FSO及RF任一信道质量较好,都可以改善系统误码率,如平均信噪比为15 dB时,强湍流及弱RF衰减(m=3)时,系统误码率为2.013×10-5,弱湍流及强RF衰减(m=1)时,系统误码率为2.766×10-5,相比于强湍流及强RF衰减时的误码率要低一个数量级。
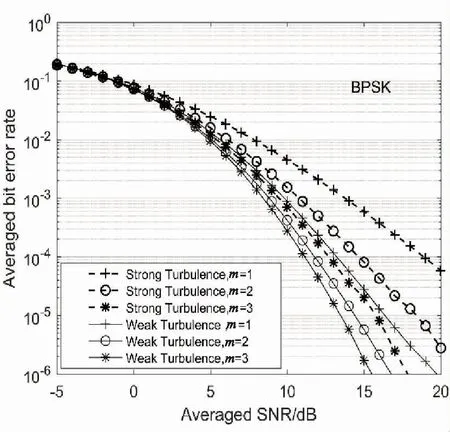
图3 不同衰落指数及湍流强度条件下平均误码率变化规律Fig.3 Average BER of the hybrid FSO/RF system with different turbulence conditions and fading figure
图4仿真分析了不同调制方式下及不同湍流强度下,混合并行FSO/RF通信系统平均误码率随平均信噪比的变化规律。仿真在RF弱衰落,m=3条件下进行。

图4 不同调制方式及湍流强度下平均误码率变化规律Fig.4 Average BER of the hybrid FSO/RF system with different modulation schemes and turbulence conditions
由图4可知,系统性能BPSK>(优于) QPSK >8PSK,即BPSK为最佳调制方式。此外,在RF弱衰落情况下,系统误码性能受M-PSK调制阶数的影响相对于湍流强度的影响较大。如当平均信噪比为15 dB时,强湍流下采用BPSK调制,系统误码率为2.013×10-5,要小于弱湍流下采用QPSK调制时的系统误码率3.817×10-5,强湍流下采用QPSK调制,系统误码率为1.705×10-4,小于弱湍流下采用8PSK时的系统平均误码率2.179×10-3。
不同通信系统方案及调制方式下,平均误码率随平均信噪比的变化规律如图5所示。仿真在强湍流及m=2条件下进行。
由图5可知,在相同的调制阶数下,混合FSO/RF通信系统的误码性能要好于单RF系统及单FSO系统,如采取BPSK调制及平均信噪比为17dB时,单RF系统误码率为2.797×10-4,单FSO系统误码率为7.947×10-3,而混合FSO/RF通信系统平均误码率为2.173×10-5。平均信噪比为20dB时,采用QPSK调制的混合FSO/RF通信系统平均误码率要低于采用BPSK的单RF通信系统及单FSO通信系统的平均误码率,一定程度上说明了信噪比较高时,混合FSO/RF传输、分集接收的通信方案对误码性能的改善要优于低阶调制方式对误码性能的改善。

图5 不同通信系统及调制方式下平均误码率变化规律Fig.5 Average BER of the hybrid FSO/RF,RF-only and FSO-only systems with different modulation schemes
5 结 论
本文针对基于SC分集技术的混合FSO/RF航空通信系统、链路性能开展研究。基于Exponentiated Weibull大气湍流分布模型及Nakagami-m衰落信道模型,利用Meijie′s G函数性质推导得到了系统的中断概率和平均误码率的闭式表达式,并进行仿真分析。仿真结果表明,与各种湍流强度下的单FSO系统及各种衰落强度下的单RF系统相比,基于SC分集的混合FSO/RF航空通信系统有效地利用了FSO及RF链路在不同大气信道条件下的互补性质,具有更优的误码性能和中断性能;采用低阶的M-PSK调制能有效地降低大气湍流对混合FSO/RF航空通信系统性能的影响;信噪比高时,并行传输、分集接收的通信方案对系统误码性能的改善要优于低阶调制对误码性能的改善,航空通信系统设计中可优先考虑通信系统传输模型,再考虑调制方式。在实际应用中,可以利用推导的性能指标闭合表达式,估计系统性能,为混合激光/射频航空通信系统的设计提供参考。

