基于自适应鲸鱼优化算法结合Elman神经网络的股市收盘价预测算法

朱昶胜，康亮河*，冯文芳

（1.兰州理工大学计算机与通信学院，兰州730050； 2.兰州理工大学经济管理学院，兰州730050）

（∗通信作者电子邮箱kanglianghe@126.com）

0 引言

随着信息技术与网络技术的快速发展，各行各业的数据呈爆炸式增长，例如各种数值数据、文本、音频、图像等，如何对非结构化数据进行挖掘是目前的一个技术热点也是难点［1］。作为近年来新兴的研究领域，通过挖掘网络舆情进行股市预测是一个有价值的研究领域［2］。由于股票市场的不确定性和不可预见性，股票市场收盘价的预测是股票交易市场中最重要、最具挑战性的问题之一。金融领域的许多分析和假设表明，股票收盘价是可预测的［3］。在传统股票市场中，预测股票的收盘价使用大量反映经济运行的结构数据，如开盘价、成交量、价格指数等。随着大数据带来的数据量和数据类型的增加，传统的简单静态股市数据已经逐渐不能满足分析和预测的需要［4］。因此，如何挖掘股市网络舆情，并利用机器学习算法或深度学习算法准确有效地预测股票收盘价，对投资者具有重要意义。

在过去的几十年里，许多模型和技术被用来预测股市的收盘价。Renault［5］研究了投资者情绪与股票收益之间的关系，他通过情感词典计算投资者情绪值，并预测标准普而500指数的回报率，实验证明在线投资者情绪是驱动股指收益的一个重要因素；Bollen等［6］通过文本挖掘技术从大量的微博评论中挖掘公众的情绪状态值，实验证明公众的情绪值可以从大规模的微博信息中提取并量化，其量化值可以用来预测股指的价格；Kao等［7］采用小波变换选择属性，并利用多元自适应回归-支持向量回归（Multivariate Adaptive Regression Splines-Support Vactor Regerssion，MARS-SVR）模型对两个新兴股市和两个成熟股市的股价进行预测，实验发现该组合模型比SVR、logistic回归及随机森林具有更高的预测精度；李振平等［8］在2016年提出了一种基于灰色关联神经网络和马尔可夫模型的股票价格预测模型，通过灰色关联分析遴选技术指标，利用误差反向传播神经网络（Back Propagation Neural Network，BPNN）对价格进行粗预测，最后利用马尔可夫链模型对收盘价作精预测，实验表明该模型不仅有效提高了预测精度还降低了计算复杂度；Yu等［9］运用文本分析技术计算万科A股（SZ00002）的股市评论的情感值，并利用BPNN模型预测了股票收盘价。刘健等［10］将粒子群优化（Particle Swarm Optimization，PSO）算法、非线性独立成分分析算法（Nonlinear Independent Component Correlation Algorithm，NLICA）及BPNN三种算法结合，建立上证综指预测模型，实验证明，此组合模型比传统方法的适应性及智能性更强，且预测精度更高；Hu等［11］提出采用改进的正余弦算法（Improved Sine Cosine Algorithm，ISCA）优化BPNN的权值及阈值，并分别预测标准普尔500指数及道琼斯工业平均指数的开盘股价走势，实验表明ISCA-BPNN模型在预测开盘价方面优于BPNN、PSO-BPNN及WOA-BPNN；Bozorgi等［12］为了解决鲸鱼优化算法（Whale Optimization Algorithm，WOA）由于过早收敛而陷入局部最优的问题，采用差分进化（Differential Evolution，DE）算法来改进WOA，并采用25个基准函数进行测试，实验发现改进WOA在最终解的质量和收敛速度方面均优于其他算法；Xu等［13］利用经验模态分解（Empirical Mode Decomposition，EMD）算法及集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）算法分解了欧美及中国股市数据，发现将分解后的固有模态函数（Intrinsic Mode Function，IMF）作为模型属性集来预测股市数据，具有较好的预测性能。

目前，大部分股市收盘价的预测是基于结构化数据，如历史收盘价数据，忽略了股市网络评论对投资者及股市收盘价的影响。在属性构建方面，大多研究采用EMD来分解收盘价序列而不是分解属性序列，忽略了EMD算法本身存在的模态混叠的问题，同时在计算最终预测值时，由于累加多个不同频率的IMF的预测值而造成的误差累积的问题。另外在预测模型的构建中，基本选择BPNN或者SVR模型作为基模型，结合PSO、灰狼优化（Grey Wolf Optimizer，GWO）等优化算法作为预测模型，而忽略了BPNN及SVR本身存在的易陷入局部最优及预测精度低等问题。针对以上问题，本文在现有的研究基础上，利用文本挖掘技术采集并量化上海证券交易所股票价格综合指数（Shanghai Stock Exchange，SSE）180股指的评论信息，通过Boruta算法对属性集进行初步筛选，并利用基于自适应噪声的完全集合经验模态分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN）算法分解并重构入模属性，最后本文提出了改进鲸鱼优化算法（Improved Whale Optimization Algorithm，IWOA）结合Elman模型作为预测模型，通过引入自适应权重有效解决了WOA易陷入局部最优的问题，同时利用IWOA优化Elman神经网络的初始权值及阈值，不仅结合了Elman神经网络无线逼近的优点，同时解决了其学习速度慢及预测精度低的问题，为基于股市网络舆情的收盘价预测提供了一种新的思路及方法。

1 文本挖掘

本文以SSE180股指为研究样本，样本期间为2016年1月4日至2016年12月31日。所采用的数据分为两部分：第一部分是通过Python网络爬虫程序抓取的东方财富网的发帖信息；第二部分是从国泰安CSMAR数据库下载的180股指收盘价数据。

1.1 数据采集

本文通过Python Spyder网络爬虫［14］程序获取发帖标题、阅读数量、评论数、作者、发表日期等股票文本信息，并以.CSV格式存储在本地磁盘。

1.2 中文分词

由于Jieba分词具有分词速度快、准确率高的优点［15］，所以本文采用Python中的Jieba分词。其基本思想是：基于Trie树结构实现词图的高效扫描，根据生成句子中所有汉字可能成词的所有情况构成有向无环图（Directed Acyclic Graph，DAG），并采用动态规划算法查找最大概率路径，最后找出基于词频的最大切分组合。

1.3 去停用词

文本分析过程中，去停用词是一个非常重要的环节，删除频率高且无意义的词，而停用词表的选择是关键，本文结合了目前主流的多个停用词表去重后综合［16］，形成了新的停用词表，主要包括哈尔滨工业大学停用词表、四川大学机器智能实验室停用词库、百度停用词表等。

1.4 计算词语权重

词频-逆文本频率指数（Term Frequency-Inverse Document Frequency，TF-IDF）［17］算法用于评估一个词对一个文件集或语料库的重要程度。TF是词在文档d中出现的频率，IDF是词在文档集中普遍性的度量。

1）TF计算公式：

tf(w，d)=count(w，d)/size(d) （1）

其中：count(w，d)是词w在文档d中出现的次数，size(d)是文档d中总词数。

2）IDF计算公式：

idf=log(n/docs(w，d)) （2）其中：docs(w，d)是词w出现的文件数，n是文档总数。

3）TF-IDF计算公式：

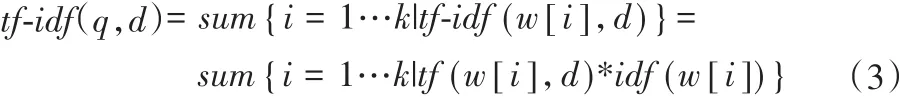
其中q是关键词w[1]w[2]…w[k]组成的查询串。

1.5 文本表示

向量空间模型（Vector Space Model，VSM）［18］是一种常用的 文 本 表 示 方 式 ，给 定 一 个 文 本D(T1，W1；T2，W2；…；Tn，Wn)，其中Ti(i=1，2，…，n)是互不相同的词条，Wi(i=1，2，…，n)是词条对应的数值。本文将交易日的文本表示为多维向量，每一个维度为一个特征词，维度值为该值在文本中的TF-IDF值，如表1所示。

表1 文本表示Tab.1 Text representation

2 算法分析

2.1 CEEMDAN算法

CEEMDAN算法是由EEMD算法发展而来，EEMD算法是在EMD中多次添加白噪声信号，将分解得到的IMF分量求平均值作为最终的实际分量，不仅改善了EMD算法存在的模态混叠现象，同时有效避免了EEMD算法添加噪声后由于不能被完全消除而引起的重构误差［19］。本文利用CEEMDAN算法实现了属性的分解及重构，其处理流程如图1所示。

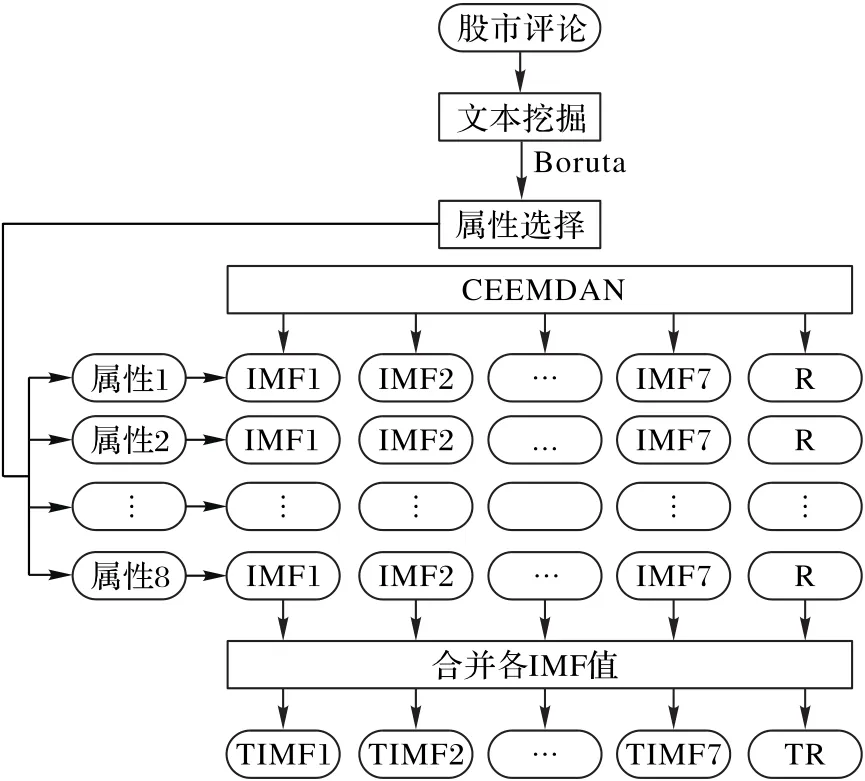
图1 CEEMDAN算法流程Fig.1 Flowchart of CEEMDANalgorithm

第一步 本文通过文本挖掘及量化共得到109个属性值，通过皮尔森（Person）相关系数去除了23个共线属性，初步得到一个86维的属性集；

第二步 利用Boruta算法选择了20个重要属性，根据各属性对收盘价贡献率的大小，选择贡献率较高的8个属性作为入模属性集；

第三步 利用CEEMDAN算法分解各属性序列，每个属性序列被分解为反映其不同频率的7个IMF分量和1个R余项；

第四步 合并各属性相同频率的IMF分量值，作为最终入模的属性值，如合并8个属性的高频IMF1分量，得到反映收盘价序列的高频TIMF1分量，最后将余项R合并，形成总余项TR，最后将集合[TIMF1，TIMF2…，TIMF7，TR]作为最终建模属性集。

2.2 WOA

WOA是模拟座头鲸社会行为的一种启发式算法。鲸鱼被认为是世界上最大的哺乳动物，曾在鲸鱼大脑的某些区域发现纺锤形细胞，这不仅可以区分鲸鱼和其他生物，而且也可以使它们像人类一样不断学习、思考、判断和交流，大多数座头鲸喜欢捕食磷虾和靠近水面的小型鱼群［20］。根据研究发现，座头鲸采取一种特殊的捕猎策略，即泡泡网捕食法，其虎头鲸的捕食过程如图2所示。在第一个阶段，座头鲸潜入大约12 m的深水中，在猎物周围形成螺旋状的气泡，在气泡网捕食法中被称为“向上螺旋”法。在后一阶段中，座头鲸快速游向水面捕获食物，这种行为被称为“双环”，包括三个不同的阶段：珊瑚环、长尾环和捕获环。WOA使用一组随机候选解，通过包围猎物、螺旋更新位置和搜索猎物更新每个步骤中候选解，直至最优解。

图2 座头鲸的捕食过程Fig.2 Huntingprocess of humpback whales

1）包围猎物。

假设鲸鱼的位置是W（i i=1，2，…，m），m是搜索空间中鲸鱼的数量，最佳位置是最佳解决方案或接近最佳位置［21］的最优方案。在定义了最佳搜索代理之后，其他搜索代理将尝试向最佳位置更新，如式（4）所示：

其中：t是当前迭代次数，A和C是随机系数，X*(t)表示猎物的位置，X(t)表示当前鲸鱼的位置，a在迭代过程中从2线性递减到0，r是[0，1]中的随机数。

2）螺旋更新位置。

WOA在开发阶段采用螺旋更新位置法，如图3所示。假设鲸鱼的位置是X(t)，猎物的位置是X*(t)。通过创建一个螺旋方程来模拟座头鲸的螺旋运动，螺旋方程如式（5）所示：

式（5）中：D表示猎物跟鲸鱼之间的位置，X*(t)表示目前位置的最佳位置，X(t)是当前位置，b是一个定义螺旋形状的常数，l是区间[-1，1]中的一个随机数。

鲸鱼以螺旋形游向猎物的同时还要收缩包围圈，假设有Pi的概率选择收缩包围机制和1-Pi的概率选择螺旋模型来更新鲸鱼的位置，其数学模型如下：

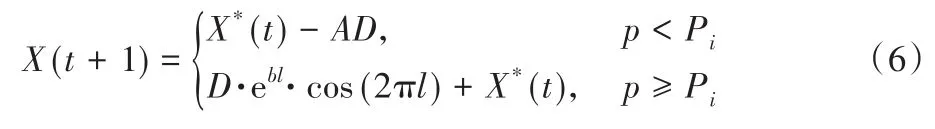
式（6）中Pi表示选择收缩包围圈的概率。

图3 螺旋更新位置法Fig.3 Spiral position updatingmethod

3）搜索猎物。

座头鲸在探索过程中随机寻找猎物，并根据随机选择的搜索代理而不是最佳搜索代理更新位置。如果|A|＞1，根据式（7）更新位置；如果|A|＜ 1，根据式（5）更新位置。

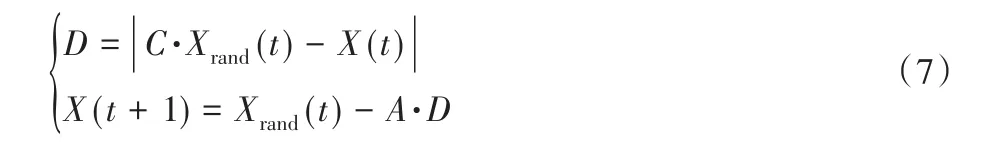
其中Xrand(t)表示鲸鱼的随机位置。

2.3 改进WOA

WOA是一种结构简单、调节参数少且全局寻优能力强的群体智能优化算法，但因其随机选择初始位置以及采用恒定的权重，导致其收敛速度慢且易陷入局部最优。研究发现，权重是WOA中的一个非常重要参数，采用恒定权重会降低WOA的效率，若权重较大，则不利于局部开采；若权重较小，则不利于全局优化。在此基础上，本文提出了一种自适应权重，以保证算法在迭代过程中有合适的非线性权重［22］，权重w随着迭代次数的增加而递减，使得迭代前期利于全局搜索，迭代后期利于局部寻优。由于引入的w下降的幅度很大，更加有利于算法进行局部寻优，提高收敛精度和加快收敛速度，其自适应权重定义如式（8）所示：

其中：wmin是最小权重，wmax是最大权重，r是[0，1]中的随机数，t是当前迭代次数，Maxiter是最大迭代次数，位置更新公式如下所示：

包围猎物：

螺旋更新：

2.4 IWOA-Elman模型

Elman神经网络是一种局部反馈递归神经网络，包括输入层、隐藏层、承接层和输出层，由于其良好的动态记忆和时变能力，自1990年Elman首次提出以来，Elman神经网络在时间序列预测中得到了广泛的应用，但由于随机选择初始值和阈值，且采用梯度下降法寻优，其网络学习速度较慢且预测的精度比较低。本文利用IWOA优化Elman神经网络的初始权值及阈值，提高了Elman神经网络的预测精度，其中图4是IWOA-Elman模型的具体流程。

第一步 初始化Elman网络所需参数，并新建Elman网络，net=newelm（minmax（input），［11，1］，｛'tansig'，'purelin'｝，'traingdx'），其中input是训练集数据，tansig是隐藏层的激活函数，purelin是输出层激活函数，traingdx是梯度下降函数；

第二步 初始化IWOA各参数，包括鲸鱼的数量m、最大迭代次数Maxiter，参数的上界ub及下界lb；

第三步 IWOA通过包围猎物、螺旋更新位置及搜索猎物不断迭代优化网络，直到迭代结束形成最优个体，其中最优个体包括权值w1、w2及w3，阈值b1和b2；

第四步 Elman神经网络解析最优个体，利用解析后的权值及阈值训练Elman神经网络并预测股市收盘价。

图4 IWOA-Elman算法流程Fig.4 Flowchart of IWOA-Elman algorithm

3 实验结果及其讨论

3.1 实验数据及评价指标

本文选择均方根误差（Root Mean Square Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）及平均绝对百分比误 差（Mean Absolute Percentage Error，MAPE）作 为 评 价指标［23］：

其中：yi表示某一时刻股票收盘价的实际值，ŷi表示某一时刻收盘价的预测值，N表示预测时刻的数量或度量。

3.2 参数设计

在Elman算法中，隐藏层的激活函数为tansig(x)=2/(1+exp(-2x))-1，输出层的激活函数为purelin(x)=x，隐藏层的个数利用经验公式m=n+l+∂计算，其中n为输入层个数，l为输出层个数，∂为1～10的常数，经测试，当m=11时预测误差最小。最大训练次数为100，误差目标为0.0001，学习率为0.1。

在IWOA中，鲸鱼数量m=30，最大迭代次数Maxiter=30，在自适应权重中，wmin=0.1，wmax=0.55。

3.3 实验结果及讨论

1）重要属性及数据特征。

以2016年1月4日至12月9日共229组数据作为训练集，2016年12月12日至12月30日共15组数据集为测试集。利用Boruta算法共筛选出20个重要属性，选取前8个作为建模属性指标。表2是8个属性的数据特征，包括极大值（max）、极小值（min）、均值（mean）、下四分位数（25%）、上四分位数（75%）和四分位范围。

2）属性分解。

图5中，（a）是CEEMDAN算法对属性“退市”中分解得到的各IMF分量和余数R；（b）将8个属性全部分解后，合并其相应的IMF分量跟余项R，得到的总TIMF分量和总余项TR。

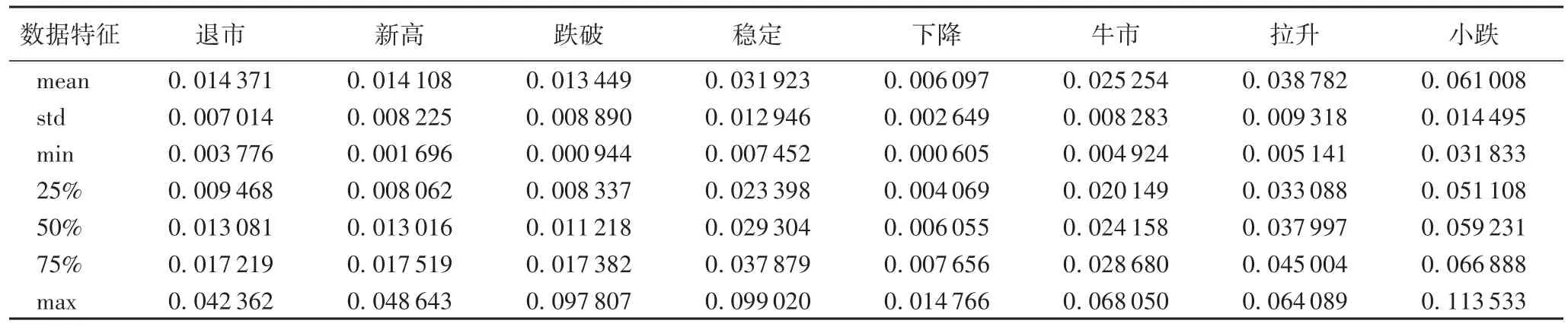
表2 属性集的数据特征Tab.2 Data characteristicsof attributes set

在CEEMDAN算法中，加入500组标准差ε0=0.2的白噪声来分解属性序列。图5（a）是对Boruta算法初步选择出的属性集中属性“退市”采用CEEMDAN算法进行分解，得到7个IMF分量和1个R余数，IMF分量由高频到低频排列，分别代表原始属性序列的噪声信号、趋势信号及低频信号，其中，横坐标代表243个交易日，纵坐标代表频率的大小。图5（b）是将Boruta算法选择出的8个属性全部利用CEEMDAN算法分解，将分解后各属性值中相近的IMF值合并所形成新的IMF分量及R余项，即将各属性中低频IMF合并形成新的低频TIMF分量，高频IMF分量合并形成新的高频TIMF分量，余项R合并形成新的R余项，最后将合并后的分量作为新属性，并将属性集[TIMF1，TIMF2，…，TIMF7，TR]作为建模属性集。

3）权重对WOA的影响。

在图6中，图6（a）是分别采用恒定权重和自适应权重时，WOA-Elman模型的预测误差MAPE的对比。图6（b）是在IWOA中，当wmin=0.1，wmax∈ [0.2，0.9]时，随机三次实验的预测误差MAPE的对比分析。在图6（a）中，若WOA采用恒定权重，MAPE的波动比较大，且其值比采用自适应权重时要大，可见权重对WOA的影响比较大。图7（b）中，当wmin=0.1，wmax∈ [0.2，0.9]时，在实验一中，随着wmax的增加，IWOA的预测误差MAPE出现了波动，但当wmax=0.6时，预测误差MAPE趋向于最小值，实验二与实验三有相同的规律，可见MAPE虽有波动，但当wmin=0.1，wmax=0.6时，MAPE具有最小值。的适应度值是150.6，而IWOA在迭代7次时开始收敛，且适应度值为141.82，相比WOA，IWOA具有较快的收敛速度，且收敛精度明显高于WOA。由此可知，采用自适应权值来优化WOA，有效解决了WOA收敛速度慢且收敛精度低的问题。

图5 CEEMDAN算法的属性分解及重组过程Fig.5 Attributedecomposition and reorganization process of CEEMDANalgorithm

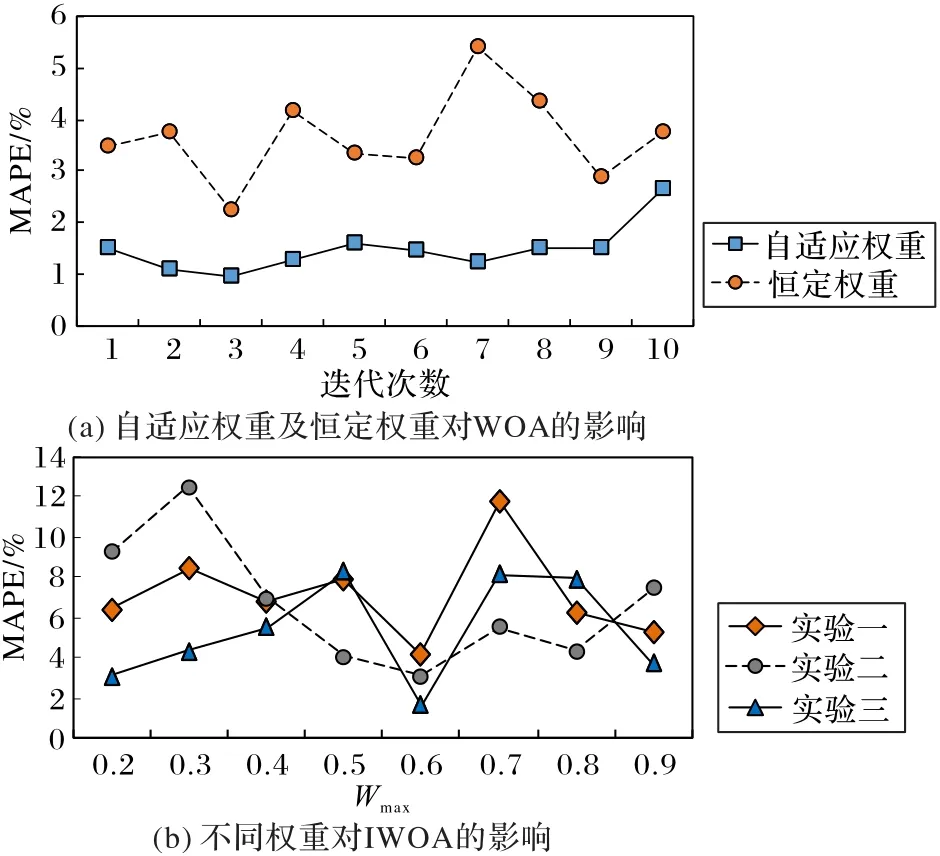
图6 权重对WOA和IWOA的影响Fig.6 Influenceof weight on WOA and IWOA

图7 WOA-Elman和IWOA-Elman模型的适应度分析Fig.7 Fitness analysis of WOA-Elman and IWOA-Elman models

4）适应度分析。

图7是WOA-Elman模型与IWOA-Elman模型的适应度值，通过分析发现，WOA在迭代到24次时开始收敛，其收敛时

5）IWOA-Elman预测结果。

图8是Elman神经网络及其优化算法的预测结果对比，Acutal表示实际收盘价。经分析发现，IWOA-Elman模型的预测值与真实值的误差最小，也最接近实际收盘价Acutal，WOA-Elman和IWOA-Elman的预测结果明显优于Elman模型，且IWOA-Elman模型的预测效果明显比WOA-Elman模型更接近实际收盘价。

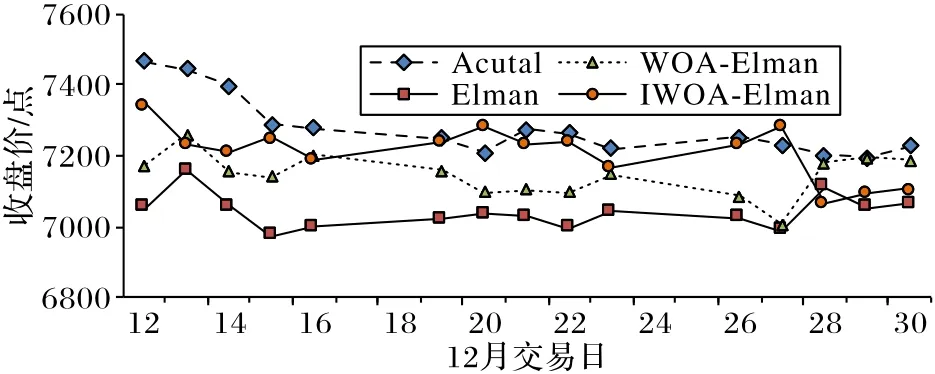
图8 Elman及组合模型预测结果Fig.8 Prediction result of Elman and combined models

3.4 对比讨论

1）预测结果对比。

采用多种算法来对比分析基于CEEMDAN算法的IWOAElman模型的性能，针对预测模型，采用SVR、BPNN来对比分析Elman模型，并采用遗传算法（GA）来对比分析优化算法IWOA，同时采用EMD算法及未采用任何数据分解算法的原始数据来对比分析CEEMDAN算法，其中表3是基于CEEMDAN算法的各模型的预测结果，表4是基于EMD算法的各模型的预测结果，表5是基于原始数据的各模型的预测结果。

分析表3，在预测的15个工作日的收盘价中，IWOAElman模型有9个预测值最接近于真实值（Acutal），主要集中在12月14日至12月27日，WOA-Elman模型有3个，GAElman有3个，BPNN有1个，从对比实验可以看出，组合模型的预测结果明显优于BPNN、SVR及Elman模型，分析表4与表5，发现相同的规律，所以本文提出的基于CEEMDAN算法的IWOA-Elman模型在基于股市网络舆情的股市收盘价预测中是十分有效的。

表3 CEEMDAN数据集上各模型预测结果Tab.3 Prediction resultsof different modelson CEEMDANdataset

表4 EMD数据集上各模型预测结果Tab.4 Prediction results of different models on EMDdataset

2）预测效果对比。

为了进一步评估IWOA-Elman模型的性能，使用图10来比较不同预测模型和基于不同数据集的预测效果。

在图10中，（a）是Elman与BPNN和SVR模型的比较，其SVR的预测结果具有较大的波动，说明算法的稳定性差；BPNN的预测值均大于实际值，但与真实值的波动趋势较接近；Elman和BPNN的预测结果的优劣不显著。（b）是优化算法GA、WOA和IWOA的比较，其GA-Elman模型的预测值均大于真实值Acutal，且相比WOA-Elman与IWOA-Elman模型，与真实值之间的误差较大；IWOA-Elman的预测效果明显优于WOA-Elman模型。（c）是基于不同数据集的WOA-Elman模型的预测结果对比，其数据集包括由CEEMDAN算法、EMD算法分解及合并后得到的数据集，以及原始收盘价Original数据集。可以发现基于Original数据集WOA-Elman模型的预测结果波动性很大，基于CEEMDAN数据集的预测值明显优于EMD数据集。（d）是基于三个数据集的IWOA-Elman模型的比较，经分析发现图（d）与（c）有相同的规律。结果表明，基于CEEMDAN算法的IWOA-Elman模型具有较高的预测精度和较好的预测效果。

3）预测误差表。

表6是各预测模型误差的评估，误差指标主要包括RMSE、MAE和MAPE。

图10 不同预测模型和基于不同数据集的预测效果对比Fig.10 Prediction performancecomparison of different prediction modelsbased on different datasets

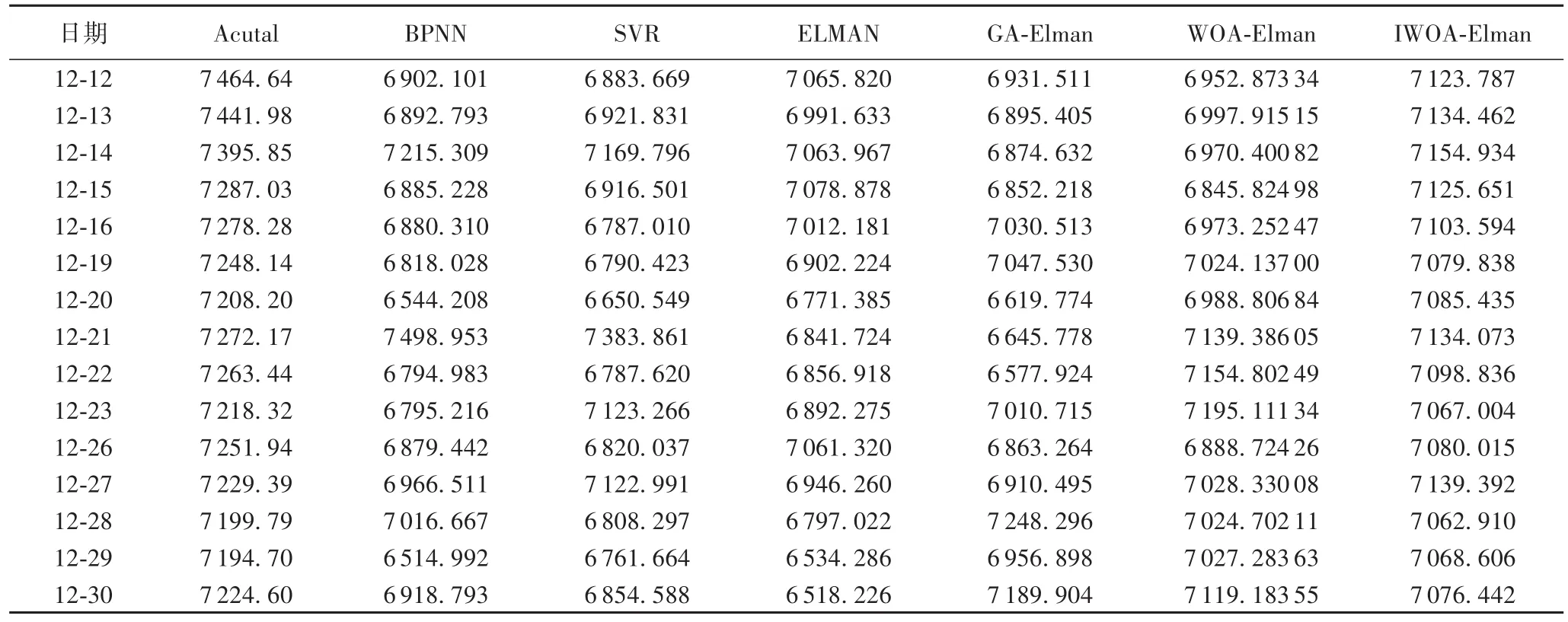
表5 原始数据集上各模型预测结果Tab.5 Prediction resultsof different modelson original dataset

表6 各模型预测误差表Tab.6 Prediction errors of different models

从表6可以看出，基于CEEMDAN数据集的IWOA-Elman模型，其RMSE、MAE和MAPE分别为145.6567、113.055 3及1.445 31，与其他预测模型相比，具有最小的预测误差。与单个预测模型SVR、BPNN和Elman相比，基于CEEMDAN数据集的IWOA-Elman模型，其MAPE分别降低了2.277 6%、1.6691%和1.8711%。与优化算法GA、WOA相比，本文提出的IWOA-Elman模型的MAE分别降低了77.119 2和39.833 5。同时，基于数据集CEEMDAN的各模型的预测结果明显优于基于EMD数据集及Original数据集，与EMD数据集和Original数据集相比，基于CEEMDAN数据集的IWOA-Elman的RMSE分别降低了3.945 6和129.115。通过以上分析，基于CEEMDAN的IWOA-Elman模型在股票网络舆情预测中是非常有效的。

4 结语

本文以非结构化股市网络舆情为研究对象，通过文本挖掘技术对其进行量化，并通过Boruta算法选择了8个重要属性。利用CEEMDAN算法对原始属性进行分解并重构各IMF分量，采用重构后从低频到高频共7个IMF分量作为各预测模型的入模属性。通过自适应权重对WOA的恒定权重进行了改进，从而大大提高了WOA的收敛速度及预测精度，并利用改进后的WOA优化Elman神经网络的初始权重和阈值，最后采用优化算法IWOA-Elman预测2016年12月12日至12月30日共15个工作日的收盘价，并通过多个预测模型及数据集进行对比分析，主要包括BPNN、SVR及GA预测模型，EMD数据集和Original数据集。实验表明，本文提出的基于CEEMDAN算法的IWOA-Elman预测模型具有较高的预测精度，证明了该模型的可靠性和有效性。