基于模糊测度和模糊积分的武器论证决策方法

孙永芹，张陕辉，申江江，王明明

(1.中国人民解放军91206部队，山东 青岛 266108； 2.海军潜艇学院，山东 青岛 266071)

武器型号论证，需要在多个方案中选出最优的决策方案，但是在实际决策过程中，决策数据涉及面广，通常涉及武器性能、目标、功能、结构、效能、费用和风险等多方面因素，而且各个因素往往不确定又有一定的关联等等。这些不确定性问题以及决策属性的相关性问题会直接导致决策结果不理想。那么，如何在数据信息不确定的情况下，对多个方案进行迅速且能实现预期目的的最优决策，成为武器论证决策研究亟待解决的问题。于是，诸多学者采用不同方法从不同角度进行了研究，取得了一些成绩[1-4]，其中人工智能技术[5-9]被用于解决这些问题，智能决策逐渐成为研究的热点。

针对以上问题，本文引入模糊测度和模糊积分理论，解决决策属性的冗余和相关性问题，提出一种适用于武器型号论证的智能决策方法。

1 模糊测度和模糊积分

1.1 模糊测度确定决策属性的重要性

1974年，日本学者Sugeno为解决属性之间存在关联而又不具备可加性的多属性决策问题，提出了模糊测度[10]，它可以表示一个或多个属性的综合重要程度，可以更加准确地描述多个属性之间的相互关系[11-12]。因此，基于模糊测度属性重要性模型可以更准确地表示各属性的重要程度。各个武器论证决策属性往往不是相互孤立的，而是相互关联的。因此引入模糊测度描述各属性的重要程度。其定义如下：

定义1：设(X,F)为一可测空间，F为X的所有子集组成的σ-代数，g是F上的一个模糊测度，如果存在λ>-1，∀L,N⊆X,L∩N=Φ，满足：

g(L∪N)=g(L)+g(N)+λg(L)g(N)

(1)

则称g为gλ模糊测度。若∀s∈X，则gλ(s)即是属性集s的权重或者重要程度；当λ=0，说明各属性之间相互独立，没有关系；当-1<λ<0，说明各属性之间冗余关联；当0<λ，说明各属性之间互补关联；若X={x1,x2,…,xn}为有限集合，则映射：xi→gi=g({xi})，i=1,2,…,n，称为模糊密度函数。gλ模糊测度可完全由其模糊密度函数确定，即：

(2)

1.2 模糊测度的确定

Marichal熵算法、二次规划算法、神经网络算法、遗传算法都是常用的计算模糊测度的方法，在此采用Marichal熵算法。

1.2.1计算属性的Shapley值

采用模糊测度对武器论证决策属性的权重建模时，因为属性间的不可加性，所以属性权重由Shapley值取代，用以描述决策属性在决策中的综合贡献。因此，在求解属性(集) 权重之前,首先确定常权情形下属性的Shapley 值。根据多人博弈中的 Shapley 函数[13]的定义，以及Grabisch的广义 Shapley 函数[14]的定义，基于gλ模糊测度的 Shapley 值计算如下：

若∀li∈X，gλ为定义在X上的模糊测度，那么基于gλ模糊测度的Shapley值Oi表示为：

(3)

1.2.2计算模糊测度

Marichal熵算法采用构建优化模型，通过最大化Marichal熵计算实现属性和属性集的重要程度，即属性和属性集的模糊测度。具体如下：

定义2：设X为属性集，n为X中元素个数，gλ为定义在X上的模糊测度，则：

(4)

其中，ξS(n)和μ(x)分别为：

(5)

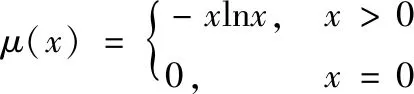
(6)

依据不同状态下决策属性的Shapley 值、Marichal熵和gλ模糊测度的定义和性质，以Marichal熵最大为目标函数，构建优化模型如式(7)所示，依据式(7)求解各指标属性的模糊测度。

(7)

式(7)中，Oi是单个属性的Shapley值。

1.3 Choquet模糊积分确定决策结果

采用模糊测度对属性和属性集的重要性建模,通常采用Choquet模糊积分进行集结计算。1954年，法国数学家Choquet针对容度定义了一种积分，即Choquet积分。而关于模糊测度的Choquet积分即看作一种模糊积分。设有限集合X={x1,x2,…,xn}，函数f为离散值函数，函数值分别为 {f(x1),f(x2),…,f(xn)}，且假设f(x1)≤f(x2)≤…≤f(xn)，则f在X上关于测度ρ的Choquet模糊积分模型[12,15]为：

(8)

式(8)中，f(x0)=0，Ai={xi,xi+1,…,xn}。

武器论证决策属性的综合集成计算使用Choquet模糊积分，运用Choquet模糊积分集结各属性函数后，由此可得方案的最终优势排序。

2 基于模糊测度和模糊积分的武器论证决策过程

基于gλ模糊测度和Choquet模糊积分理论，武器论证决策的过程设计如下：

1) 针对具体的武器论证决策问题，建立相应的属性体系，确定为决策属性因素，并进行归一化处理；

2) 采用适当的方法，取得属性的全局重要性，也就是指标的Shapley值；

3) 根据优化模型计算指标集合的gλ模糊测度；

4) 采用Choquet模糊积分，计算决策结果。

因此，基于gλ模糊测度和Choquet模糊积分的武器论证决策流程如图1所示。

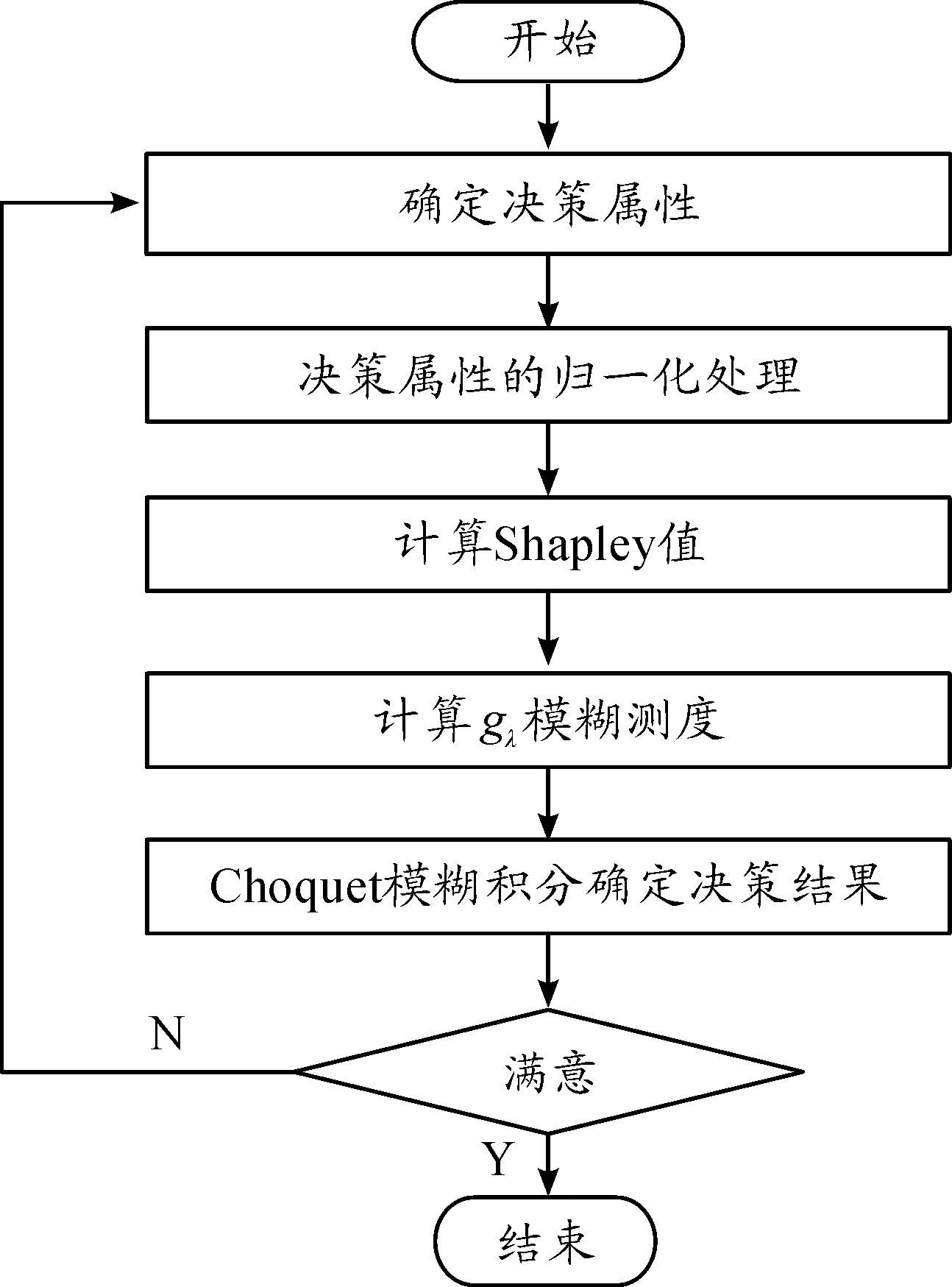
图1 基于模糊测度和模糊积分的武器论证决策流程框图

3 仿真验证分析

因为武器具体属性涉及保密问题，对某些不可知指标，在此参照雷达相关资料，设置了合理的参数，假定3个备选方案，进行验证性分析。首先，主要选取综合作战效能、费用、研制周期和风险4个指标建立决策模型，其模型构建如下：

(9)

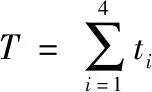
(10)

F=γ1F1+γ2F2+γ3F3

(11)

式(9)～(11)中：Ei是综合作战效能，参考文献[16]的方法，选取指挥控制能力、探测性能、综合保障性、生存能力、数据处理能力作为主要指标，由D-S证据理论确定权重和定性指标值，并把权重和指标值转化为云模型，再根据云运算规则进行计算，其计算数据如表1、表2所示，综合作战效能评价结果如表3所示；ej为第j个子指标的评估值；wj为对应的组合权重因子；T是研制周期；t1是方案阶段、t2是初样阶段、t3是试样阶段、t4是定型阶段；F是研制风险；γ1、γ2、γ3是各风险度的权重系数，且γ1+γ2+γ3=1。

费用模型采用参考文献[17]的全寿命周期费用(life cycle cost,LCC)，包括装备采购费用、装备研制费用、装备使用和保障费用。

表1 综合作战效能权重等级云表示

表2 综合作战效能评价结果等级云表示

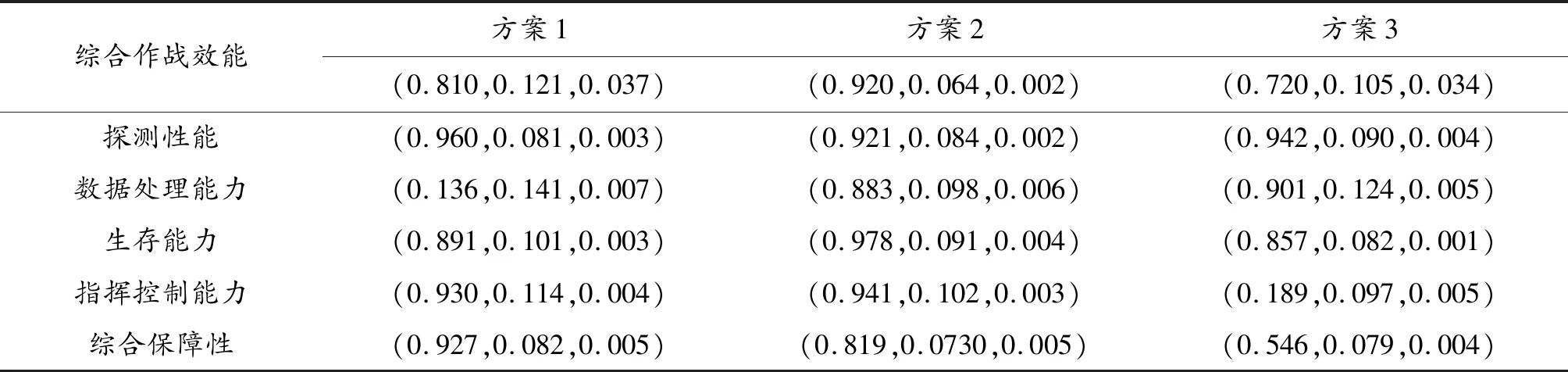
表3 综合作战效能评价结果

其次，因为综合作战效能、费用、研制周期和风险4个属性的物理量纲不同，所以，必须先进行归一化处理。综合作战效能属于效益型指标，费用、研制周期和风险属于成本型指标，其归一化处理如下：设方案集C={c1,c2,…,cn}，属性集H={h1,h2,…,hm}，决策矩阵H=(hij)m×n，hij是方案ej的第i个指标值。在此把决策矩阵转变为相对隶属矩阵，即T= (Tij)m×n，归一处理。

效益型指标：

TLj=[(hij-himin)/(himax-himin)]pi

(12)

成本型指标：

TLj=[(himax-hij)/(himax-himin)]pi

(13)

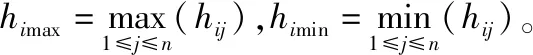
其三，通过专家和决策者打分,确定常权情形下属性Shapley值的判断矩阵R。

(14)

式(14)中，Iij表示属性hi与hj的Shapley 之比，显然Iii= 1。然后采用层次分析法[18]，判定矩阵R的一致性。当判定矩阵R满足一致性时，则依据矩阵R计算常权情形下各属性的Shapley 值，如表4所示。

表4 决策属性的Shapley值

其四，属性的模糊测度计算，根据表4和优化模型(式(7))，运用Matlab编程，求解各属性的(集)模糊测度，计算结果如表5所示。

表5 决策属性的模糊测度值

其五，用Choquet模糊积分计算方案的评估值，依据方案的评估值对方案进行排序和选优。费用、研制周期和风险的初始仿真数据如表6所示，根据表4、表5和Choquet模糊积分模型(式(8))计算决策结果，所得决策方案仿真结果如表7所示。由表7得3个方案的优势排序(由大到小)为：2，1，3，最优方案是方案2。因此，基于gλ模糊测度和Choquet模糊积分的方法可有效解决在信息不确定的情况下，快速有效的对多个方案进行最优决策的问题，可以选出最优方案，而且简单、易行。

表6 费用、研制周期和风险的初始仿真数据

表7 3个方案的属性决策结果数值

本方法与文献[17]的决策结果比较见图2，3个方案的优势排序完全相同，但相比文献[17]的方法，本方法不需要确定各属性的权重，评估结果不依赖各属性指标的权重，可以在各属性权重完全未知的情况下对方案进行选择，解决了多属性武器论证优选过程中属性权重难以确定的问题，而且能较好地描述各决策属性之间存在的相互关联现象，使决策更加客观和准确，为合理、科学地选择武器论证决策方案提供了参考。

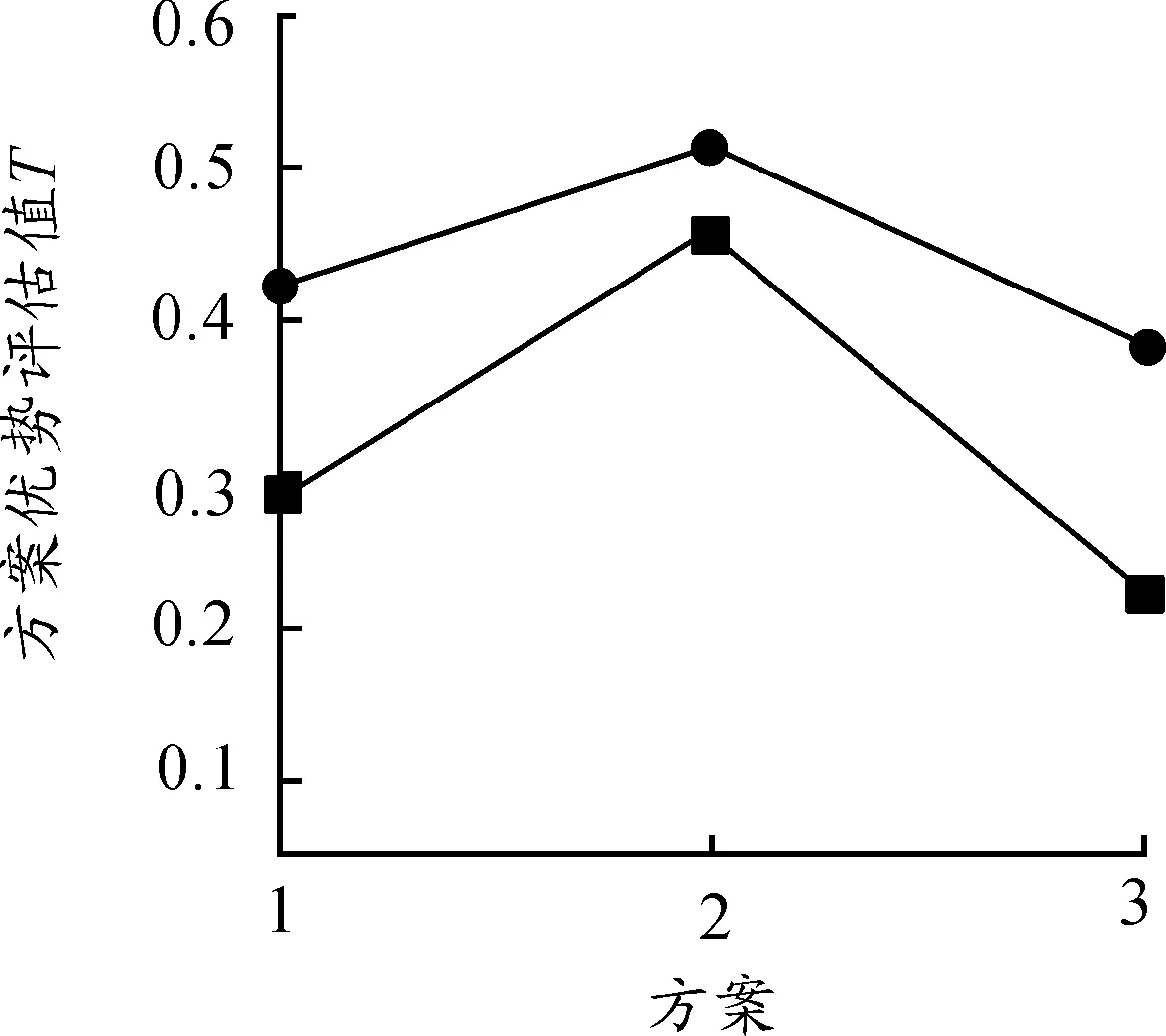
图2 与文献[17]决策方法仿真结果

4 结论

本文针对武器论证决策中，决策数据信息来源广而且具有不确定性，建立型号决策模型，优化了综合作战效能指标并进行归一化处理；模糊测度表示关联决策属性的重要程度，解决属性的相关性问题，Choquet模糊积分实现最终的决策结果。采用MATLAB进行仿真，本文的方法合理可行。