基于云模型的装备设计方案评估方法

倪子纯，狄 鹏，王 旋

(海军工程大学 管理工程与装备经济系，武汉 430033)

多属性决策问题在现实生活中普遍存在，决策者需要综合考虑几个备选方案的若干个具有制约关系的属性，对多设计方案进行综合评估并排序，优选出最佳方案。在新型装备研制初期，对多个备选设计方案进行评估优选，是典型的多属性决策问题。

当前，设计方案评估的主要方法有层次分析法、模糊综合评价法、灰色关联分析法、熵权法等，文献[1]运用了毕达哥拉斯不确定的PULWG算子和PULWA算子等开展了相关研究。文献[2]在食品生产过程中建立了区间值模糊集评价模型。文献[3]改进了蚁群聚类算法，适用于解决多属性复杂大群体聚类与决策问题。

由于存在决策者的主观认知和多变的决策环境等影响因素，决策者很难准确量化所获取的信息，上述方法存在一定的局限性。为解决评估指标存在模糊性与不确定性的问题，李德毅院士[4]于1995年在统计数学和模糊数学的基础上提出了云模型理论，可以实现定性到定量的自然转换，解决了在评估领域存在的不确定性指标难以量化的问题[5-6]，目前已被广泛应用于效能评估、风险预测和应急预测等领域[7-8]。文献[9]将云模型引入指挥控制系统效能评估中，避免了评估过程中存在的主观因素影响。文献[10]提出了正态云模型距离相似度与形状相似度概念，建立了云模型综合相似度测算框架并研究了简化算法。文献[11]通过改进黄金分割法生成云的3个数字特征，结合熵权法确定属性权重。文献[12]在军事信息系统项目军民融合决策评估模型中通过改进三标度AHP法确定属性权重，综合形状-距离相似度云模型进行评估，辅以算例证实了该方法的可靠性。由此可见，云模型已经被广泛应用且被各领域学者进行了不同程度的改进。

本文在现有的云模型评估方法础上，提出了一种基于云模型的装备设计方案评估方法。首先，采用黄金分割法将专家语言评价值转化为定量的云数字特征；其次，为避免主观因素影响，优化了一种基于云模型确定属性权重的方法，并将属性权重与各评价云融合得出综合评价云；再次，遵循云相似度原理，根据兼顾形状和距离的云模型综合相似度的大小进行方案排序。最后，结合具体算例验证该方法可行性。

1 基于云模型的决策信息转化

1.1 云模型基本概念

李德毅院士于1995年在概率论和模糊数学基础上提出了一种可以将定性语言值转化为数值进行量化描述的不确定性转换模型，被称为云模型，可同时研究模糊性和随机性以及两者之间的关系。在云模型的实际研究中主要侧重于正态云，尤其是一维正态云。

定义1[13]设U是一个用数值表示的定量论域，C是论域U上的定性概念，如果存在定量值x∈U，x为C上的一次随机实现，且对C的隶属度μ(x)∈ [0,1]是一个具有稳定倾向的随机数，则μ(x)在论域U上的分布简称为云，且每个(x,μ(x))称为一个云滴。

云模型有3个数字特征：期望Ex，熵En和超熵He，期望Ex是指云滴在论域空间分布的期望值；熵En代表着定性概念不确定性的度量，可以用来描述云的跨度，反映了云滴的离散程度；超熵He是熵En不确定性的度量，代表熵的离散程度。

定义2[14]设在论域中有n朵云{C1(Ex1,En1,He1),C2(Ex2,En2,He2),…,Cn((Exn,Enn,Hen)}，可将n朵云集结为一朵综合云C(Ex,En,He)。

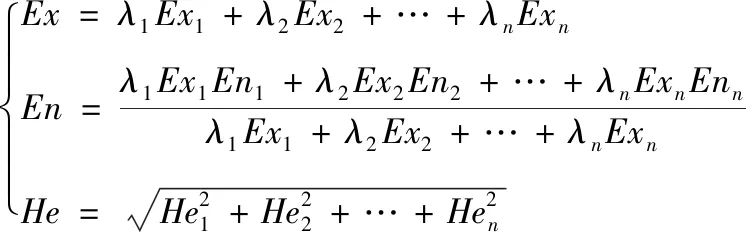
其中，λ=(λ1,λ2,…,λn)为n朵云的权重值。

1.2 基于黄金分割法的语言值转化云模型

自然语言评价值集H由n个语言评价等级组成，n一般为奇数。专家评价值的有效论域为[Xmin,Xmax]。记H={hi|i=-t,…,0,…,t,t∈N}。本文采用改进后的黄金分割法[11]生成n朵云的数字特征，具体如表1所示。

表1 黄金分割法生成云的3个数字特征

1.3 兼顾形状和距离的正态云模型综合相似度

以往的云模型相似度测算方法主要有3类：云滴距离测算法、夹角余弦法和期望曲线面积法。云滴距离测算法[14]计算量大且较为复杂；夹角余弦法[15]忽略了熵和超熵这两种数字特征；而期望曲线面积法[16]没有考虑超熵对云模型相似度的影响且计算复杂，上述方法均存在较大的误差。因此本文考虑结合云模型形状相似度和距离相似度来计算综合相似度[10]。设两朵云为Ci(Exi,Eni,Hei)和Cj(Exj,Enj,Hej)，云模型综合相似度计算方法如下：

步骤1基于正态云模型方差的形状相似度计算

(1)

为两朵云的形状相似度。

步骤2基于正态云期望的距离相似度简化计算

(1) 计算两朵云熵的比值：

(2) 查找拟合结果相关数据表[10]，可以得到距离相似度的拟合函数：

y=a×exp(-((x-b)/c)2)

(3) 计算两朵云期望之间的相对距离：

θ=|Exi-Exj|/(3(Eni+Enj))

(4) 将θ代入拟合函数，得到距离相似度：

Simd=a×exp(-((θ-b)/c)2)

(2)

步骤3计算云模型综合相似度：

Simc=Sims×Simd

(3)

2 基于云模型的属性权重优化

在多属性决策中，权重是一个非常重要的概念，指的是某一属性在整体评价中的相对重要程度。多属性决策的实质，是对多个备选方案的综合属性值进行排序。决策者对评估设计方案所有属性进行两两比较，得到判断矩阵并进行规范化后可得B=(bij)m×n。假设各属性权重向量为w=(w1,w2,…,wn)T，那么方案Si的综合属性值和权重的关系如下：

其中，wj是第j个属性的权重值。当属性值、权重值均确定时，评价矩阵中各元素转化为云的3个数字特征，综合评价值越高说明方案越优。当各属性的权重值未知时，在文献[18]提出了基于云模型的属性权重确定方法的基础上，本文引入云的三个数字特征，建立如下模型。

其中：Exij为云模型中的期望值；Enij为云模型中的熵值；Heij为云模型中的超熵；wj为各属性的权重值。此模型主要是对权重进行优化，引入熵和超熵对利用权重的平方和为1做约束条件，降低了权重的模糊性。由模型可知，当期望值越大、熵值越小、超熵值越小时，方案的综合评价值最大，即方案最优。

利用拉格朗日函数求解：

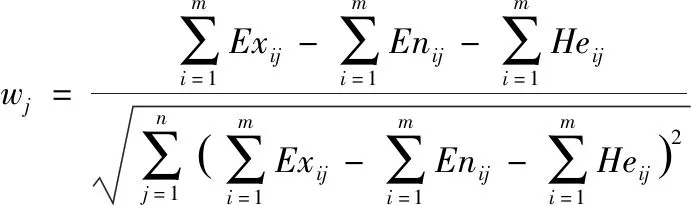
为了保证所有属性权重和为1，对权重进行归一化处理：

3 基于云模型的多属性决策步骤

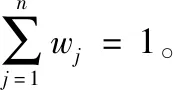
步骤1根据式(4)，确定w=(w1,…,wj…wn)。

步骤2获取专家语言评价值信息。根据表1将专家语言评价值转化为评价云模型，将专家Ek对于设计方案Xi中第j个属性的语言评价值转化为云决策矩阵Ckij(Exkij,Enkij,Hekij)。

步骤3对方案Xi中的n个属性的云模型进行第一次信息集结，得到Cki(Exki,Enki,Heki)。

步骤4获取专家组评价信息权重λk，将所有专家针对方案Xi评价云模型进行二次信息集结，得到Ci(Exi,Eni,Hei)，其中：

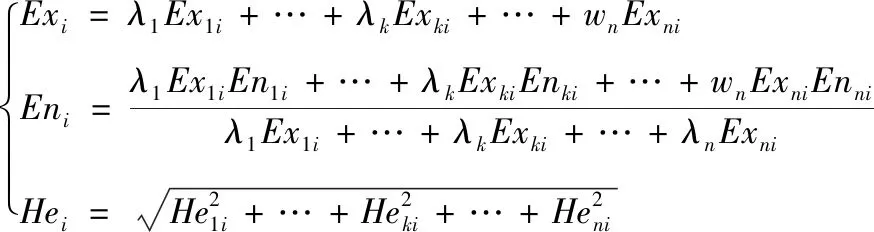
步骤5令C*=(Ex*,En*,He*)为理想云，依据兼顾形状和距离的正态云模型综合相似度计算Ci与C*的相似度，按相似度大小进行排序。

4 算例分析

研制某新型装备，有4个设计方案X={X1,X2,X3,X4}可供选择。主要考虑的因素有系统效能G1，安全性能G2，经济成本G3，保障性能G4。其中G3为成本型属性，其余均为效益型属性。在设计方案评估专家组对设计方案各属性进行语言值评价前，邀请4位在该新型装备设计领域的权威专家A={A1,A2,A3,A4}对各属性的重要程度进行评价，使用5标度语言评价集为S={s-2= 一般，s-1=比较重要，s0=重要，s+1=非常重要，s+2=极其重要}。

步骤1确定属性权重。由专家组A={A1,A2,A3,A4}对各属性的重要程度评价，可获取表2所示的语言评价值信息。

给定论域为[0,100]，He0=0.1，依据表1的黄金分割法公式表,计算生成5朵云：C-2(0,10.31,0.26)，C-1(30.9,6.37,0.16),C0(50,3.93,0.1),C+1(69.1,6.37,0.16)，C+2(100,10.31,0.26)。根据表2中专家对各属性重要程度语言评价值信息，可得表3所示的云决策矩阵。由表3可根据式(4)计算得出设计方案各属性权重集为w=(0.28,0.38,0.14,0.20)。

表2 专家对各属性重要程度语言评价值信息

步骤2确定各方案云决策矩阵。由决策小组的5位专家E={E1,E2,E3,E4,E5}对4种设计方案进行评估，每位专家在5标度的语言评价集为H={h-2=差，h-1=较差，h0=一般，h1=较好，h2=好}中选择语言评价值，对各方案进行评估，得出表4所示的语言评价值信息。根据步骤1中黄金分割法生成的五朵云，可将表5中专家组针对各方案的语言评价值信息转化为云决策矩阵分别如表5～表8所示。

步骤3计算各方案评价信息云矩阵。在云决策矩阵的基础上，结合属性权重w=(0.28,0.38,0.14,0.20)，根据式(5)对方案X1,X2,X3,X4中的4个属性云模型进行第一次信息集结，得到各专家对各方案的评价信息云矩阵如表9所示。

表3 专家对各属性重要程度评价的云决策矩阵

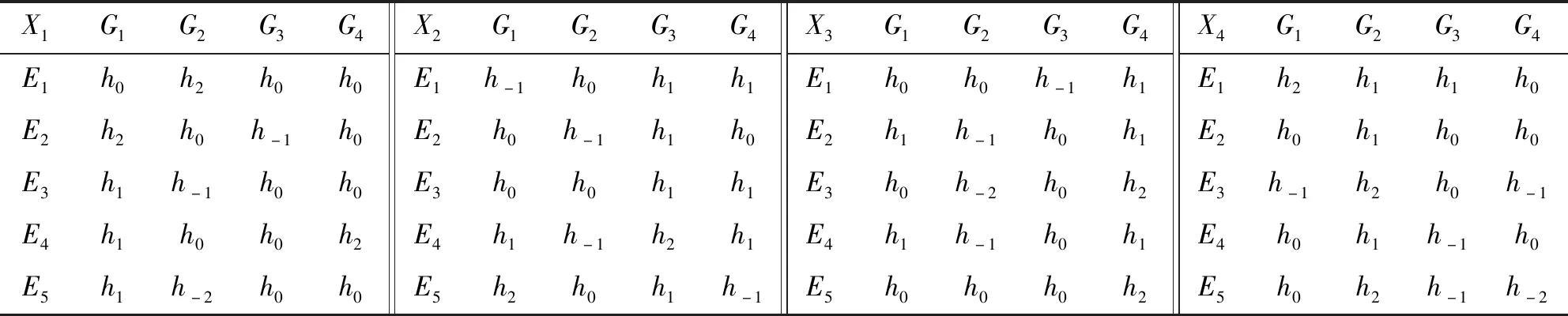
表4 专家给出的语言评价值信息

表5 方案1的云决策矩阵

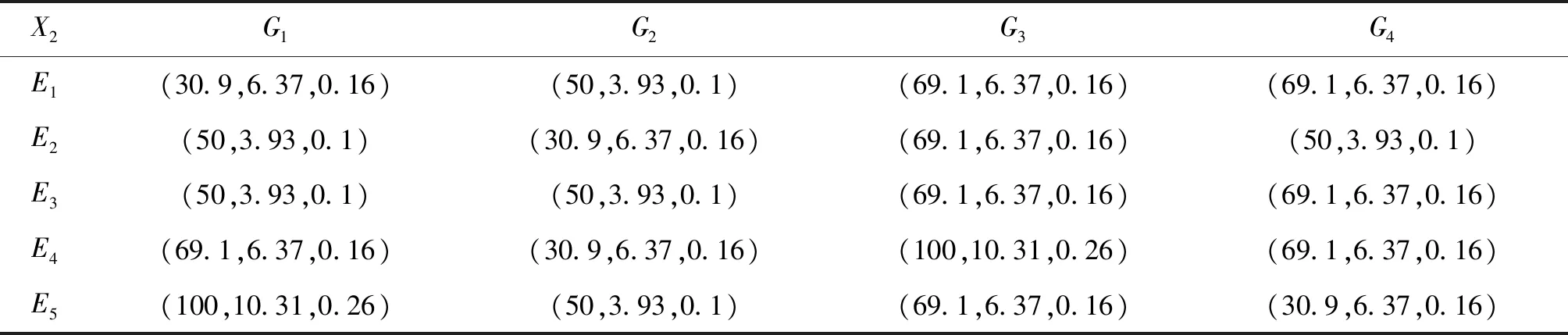
表6 方案2的云决策矩阵

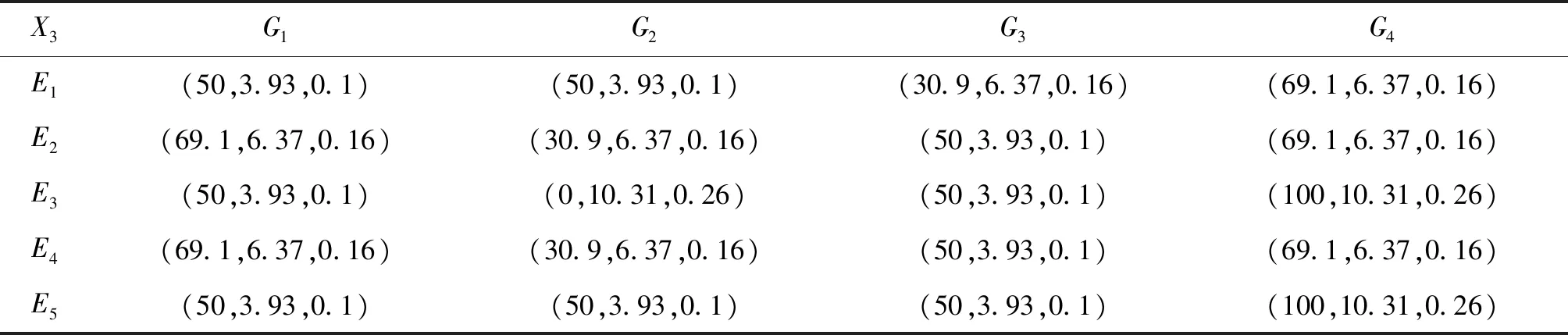
表7 方案3的云决策矩阵

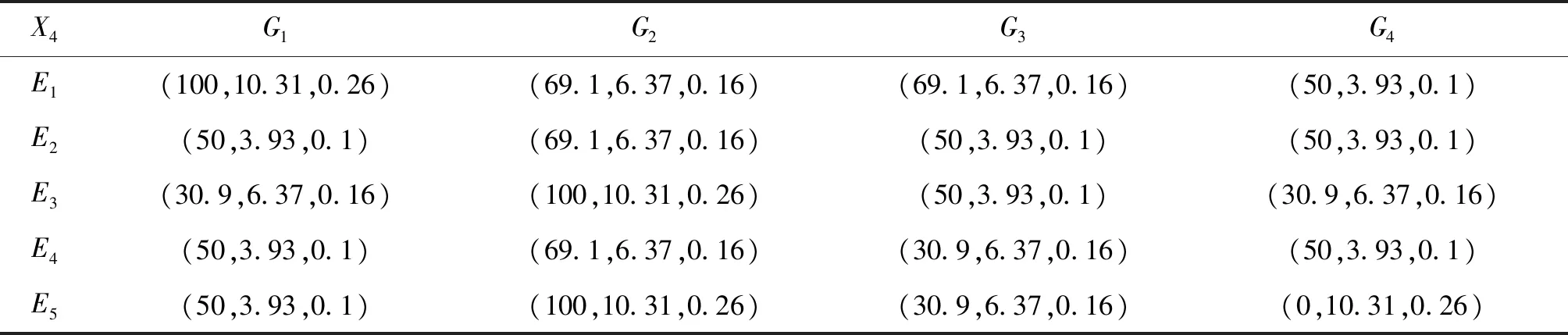
表8 方案4的云决策矩阵

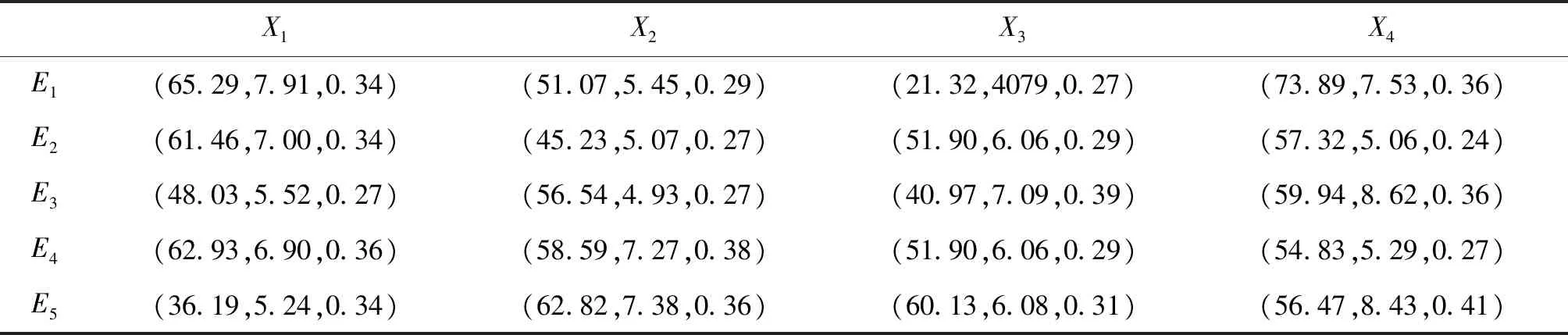
表9 各专家对各方案评价信息云矩阵

步骤4计算各方案云矩阵。根据式(6)，在各专家对各方案的评价信息云矩阵基础上进行二次信息集结。一般认为各位专家的权重相同，即λ1=λ2=λ3=λ4=λ5=0.2，得到各方案的云矩阵如表10所示。

表10 各方案云矩阵

步骤5计算各方案云矩阵与理想云相似度。本例中系统效能G1，安全性能G2和保障性能G4为效益型属性，经济成本G3为成本型属性，根据两种属性的特征，可令其各属性的云模型分别为G1(69.1,6.37,0.16)，G2(69.1,6.37,0.16)，G3(69.1,6.37,0.16)和G4(50,3.93,0.1)，结合属性权重w=(0.28,0.38,0.14,0.20)，得到理想云为C*(65.28,5.99,0.48)。利用Matlab软件绘制理想云图形，如图1所示；利用Matlab软件绘制各设计方案的综合评价云与云模型图形对比图，如图2所示；根据式(1)～式(3)可分别计算得出各方案云模型与理想云的形状相似度、距离相似度和综合相似度，如表11所示。

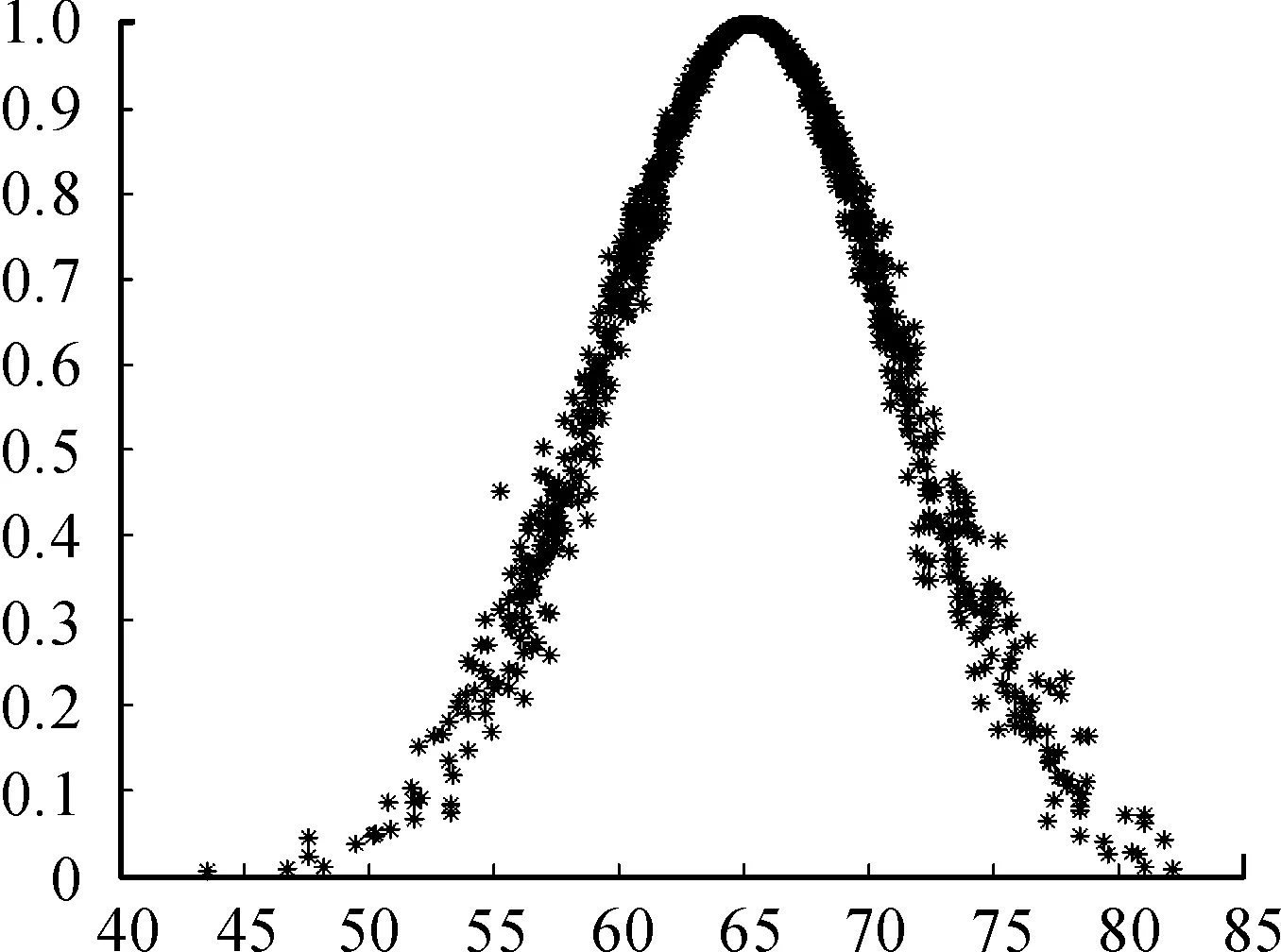
图1 理想云模型图

从表11可看出，方案X3与理想云的形状相似度最大，即形状上最为接近；方案X4与理想云的距离相似度最大，即在距离上更加贴近理想云。通过比较综合相似度大小，可看出方案4与理想云的综合相似度最大。结合图2中的4个云对比图可看出，方案X3与理想云在形状上较为接近，而方案4的云模型与理想云在距离上较为接近。这与表12中的相似度计算结果一致。因此可对4个设计方案进行排序，即方案X4>方案X2>方案X1>方案X3。通过对比综合相似度大小和云模型图形，验证了本文方法的适用性和可靠性。

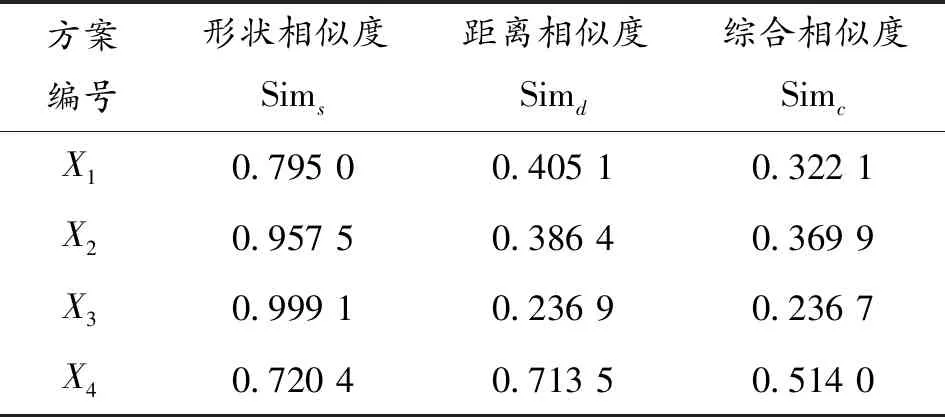
表11 各方案云模型与理想云的相似度

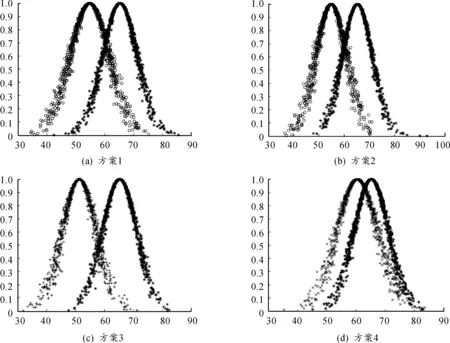
图2 各方案云模型与理想云模型图

5 结论

本文将云模型方法应用到装备设计方案评估排序中，优化了针对云数字特征的属性权重确定方法，通过计算云模型的综合相似度，对多设计方案进行综合评估。试验表明了该方法的可行性与有效性，为装备设计方案评估提供了一种新的解决思路，具有较高应用价值。