结构物-标准砂界面剪切机理及数值模拟分析

王瑞，郭聚坤,2*，卞贵建，赵树青，罗伟，刘芹

(1.山东交通职业学院 公路与建筑系，山东 潍坊 261206； 2.长安大学 公路学院； 3.日照交通发展集团有限公司)

随着高速公路、铁路等大型工程的发展，下部基础的安全施工对于整个结构愈发重要，这涉及到结构物与土体的接触问题，结构物-土界面剪切机理一直是近年来岩土工程领域研究的热点之一。

界面剪切试验是研究界面力学特性的重要途径，如梁鹏等进行了松砂-混凝土界面常/变法向应力作用下的剪切试验，分析了剪切过程中剪应力和剪切面体应变的变化特征；曹卫平等对密砂-混凝土进行了常/变法向应力作用下的剪切试验，认为在变法向应力作用下，剪应力最大值与相应的常法向应力作用下的抗剪残余强度相同，但体应变较小；Borana L等分析了不同法向应力和吸力对钢-土界面作用的影响，认为临界界面剪切强度取决于基质吸力；Farhadi B等利用直剪仪进行了钢-砂界面剪切试验，认为峰值摩擦力和最大膨胀角受层面倾斜角的影响较大；Clough等通过混凝土-砂土界面直剪试验，建立了非线性弹性双曲线模型；Morched等从宏观和细观两个角度对结构物-土界面剪切性状进行分析，提出了宏、细观界面模型；王晓妮等指出在桩-土界面作用模型中，硬化型模型一般可用向下弯折的折线进行拟合，软化型且剪胀比较明显的模型可用向上弯折的折线进行拟合；路德春等通过接触面土体在剪切过程中的软化现象与土的超固结状态之间的关系，建立了硬化与软化特性的接触面本构模型；李赛等基于改进的统计损伤模型，提出了无厚度接触面模型。

为进一步探究结构物-土界面剪切试验机理，该文通过改进的直剪设备，进行木、钢和混凝土3种桩模拟材料与标准砂的界面直剪试验，分析界面剪切应力-剪切位移关系和界面抗剪强度指标变化规律，提出符合剪切应力-位移关系的对数-双曲线模型，最后对界面剪切试验进行数值模拟。

1 界面剪切试验

1.1 试验设备改进

界面剪切试验设备是通过对室内直剪仪下盒加以改进制作而成，上剪切盒放入砂土和透水石，砂土体积为30 cm×30 cm×1.25 cm，下剪切盒放入木板、钢板和混凝土板，下剪切盒空间尺寸与结构物尺寸相同，以做到二者的紧密契合，如图1所示。

1.2 试验材料准备

试验所用标准砂为北京中交工程仪器研究所生产。其基本物理力学指标按土工试验方法标准获取，其内摩擦角为27.6°，密度为1.52 g/cm3，Cc=0.92,Cu=1.49。结构物包括木、钢和混凝土，尺寸为10.1 cm×9.6 cm×2.5 cm，其中木采用结构强度高、稳定性好的三合板加工而成；钢为Q235A碳素结构钢，产自潍坊本地钢材公司，力学性能试样取样位置及试样制备按GB/T 2975-2018执行，力学性能及熔炼成分的规定按GB/T 700-2006执行，钢材中C、Si、Mn、P、S含量分别为0.16%、0.27%、0.76%、0.025%、0.032%，脱氧方式为沸腾钢，屈服强度为245 MPa，抗拉强度为425 MPa，伸长率为30.1%；混凝土设计强度等级为C50，最终采用配合比的实测抗压强度为55.4 MPa，采用的配合比为石∶砂∶水泥∶水∶外加剂=2.79∶1.38∶1∶0.43∶0.01，经养护28 d而成，其中石粒径为5～10 mm，砂粒径为0.25～0.5 mm，水泥过0.075 mm筛，采用P.O.42.5级水泥，水采用饮用水，外加剂型号为FT-001，掺量为1.2%，减水率为27%。

1-传压螺钉；2-上剪切盒；3-下剪切盒；4-接触钢块

1.3 试验方案

下剪切盒放入木块、钢块和混凝土块，上剪切盒放入经烘箱烘干后的标准砂，为保证试验标准砂状态一致，放入标准砂的质量保持一致，然后在法向应力50 kPa作用下预压5 min，随即在法向应力50、100、150、200 kPa作用下进行剪切试验，记录测力计读数。夏春红等指出当剪切速率控制在0.02～1.2 mm/min之间时，界面剪切特性不会受到影响，此试验的剪切速率设定为0.8 mm/min。

2 试验结果分析

2.1 界面剪切应力-剪切位移关系

木、钢、混凝土与标准砂界面剪切应力-剪切位移关系如图2所示。结构物-标准砂界面试验数据见表1。

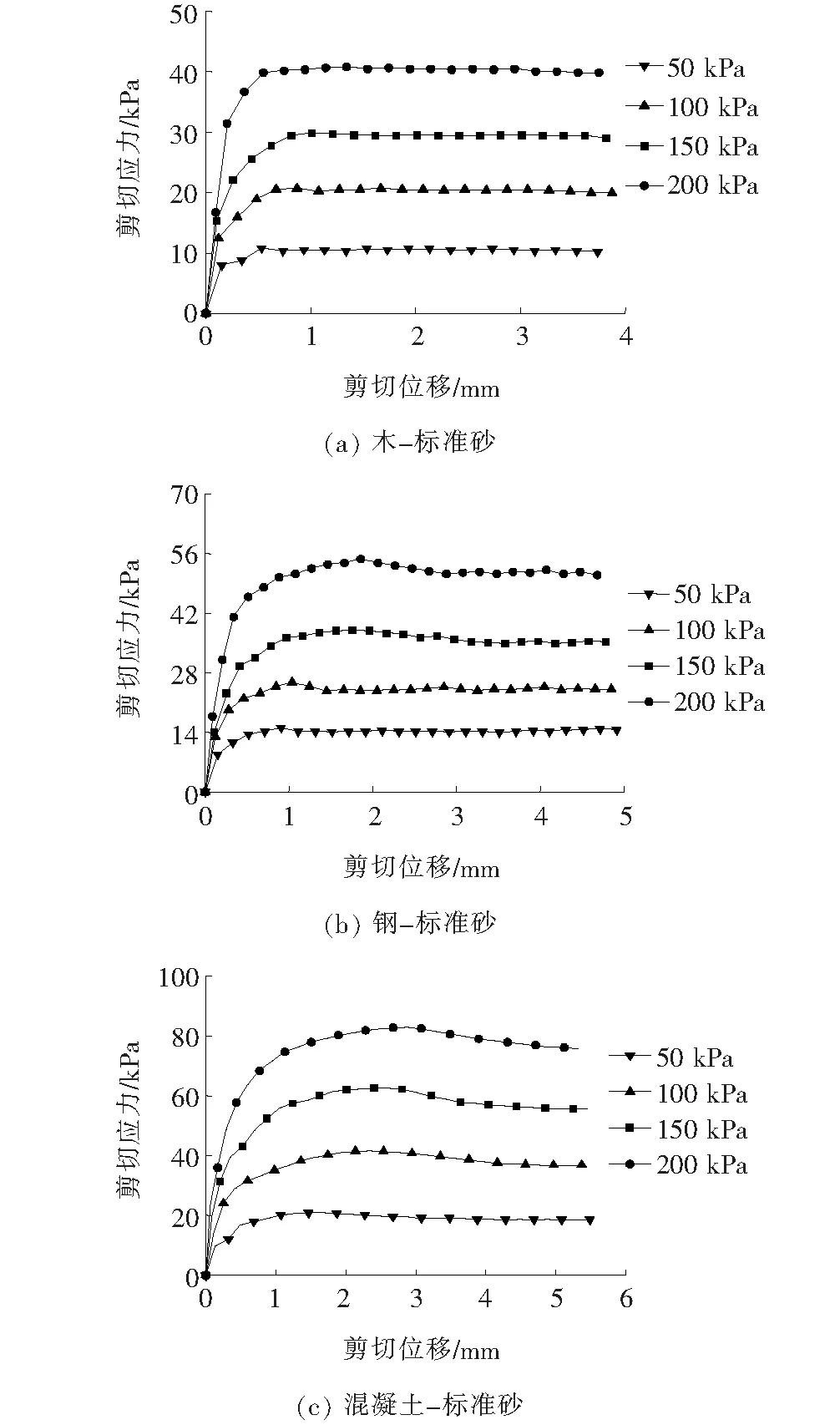
图2 结构物-标准砂界面剪切应力-剪切位移关系

由图2和表1可以看出：① 在剪切初始阶段，剪切应力随剪切位移增速较快，二者表现出很好的线性关系，随着剪切位移的增加，剪切应力增速变缓，直至达到峰值剪切应力，表现出较好的应力硬化现象。到达峰值剪切应力后，木-标准砂界面剪切应力略有减小，有轻微的软化现象，表现比较平稳，而钢-标准砂界面和混凝土-砂界面剪切应力出现较明显的软化现象，软化程度大小关系为：混凝土-标准砂界面>钢-标准砂界面>木-标准砂界面;② 随着法向应力的增大，峰值剪切应力和剪切位移也逐渐增加，两者表现出较好的正相关关系；在同一法向应力下，木-标准砂界面的峰值剪切应力和剪切位移最小，混凝土-标准砂最大，钢-标准砂居中。

2.2 界面抗剪强度指标变化规律

对于同一结构物与标准砂的界面剪切，法向应力的增加值与峰值剪切应力的增加值仍近似成直线关系，故采用摩尔-库仑破坏准则描述峰值剪切应力和法向应力的关系，经线性拟合得到界面摩擦角和表观黏聚力，如图3和表2所示。

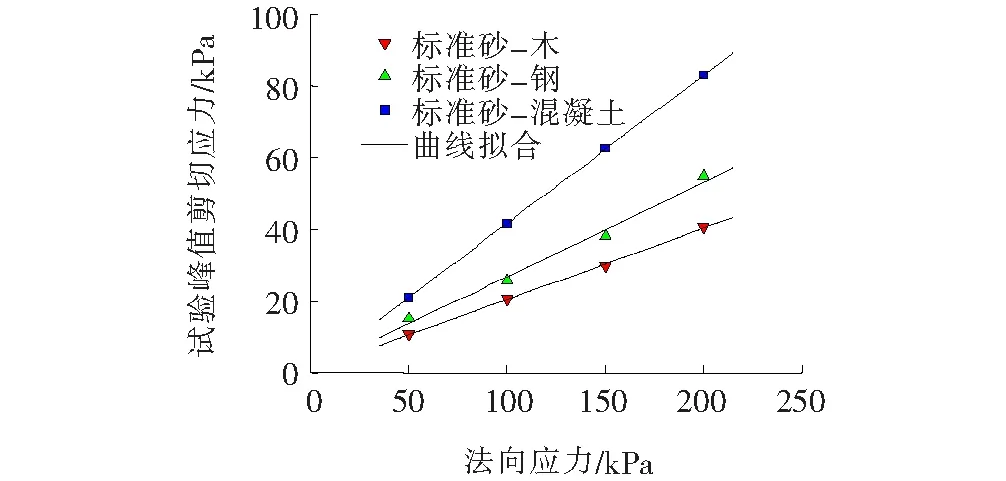
图3 界面峰值剪切应力与法向应力关系

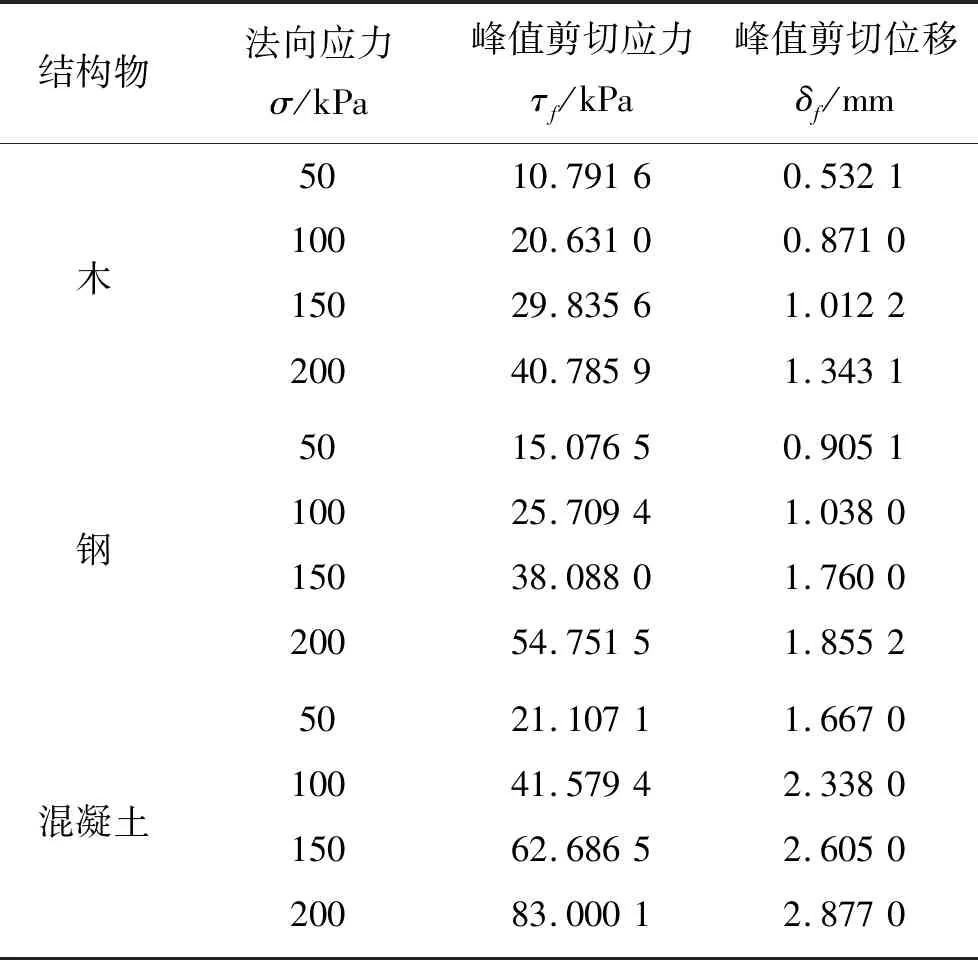
表1 结构物-标准砂界面试验数据

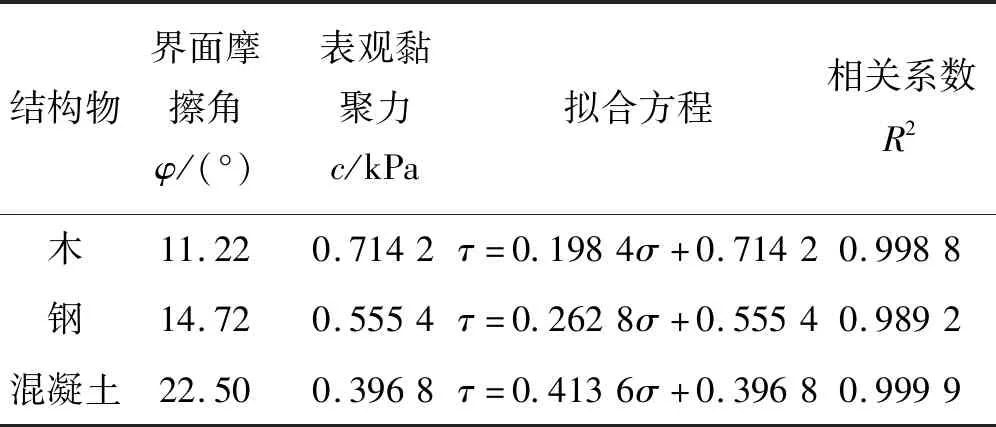
表2 结构物与标准砂接触面强度参数

由图3和表2可以看出：① 线性拟合值R2均在0.98以上，拟合效果很好，结构物-标准砂界面剪切破坏符合摩尔-库仑破坏强度准则;② 3种界面的摩擦角表现出较大的差异性，其中混凝土-标准砂界面摩擦角最大，钢-标准砂界面次之，木-标准砂界面最小，这与材料本身的属性有很大的关系;③ 3种界面的表观黏聚力集中在0～1 kPa范围内，三者差异不大，说明表观黏聚力的大小与材料本身没有关系。

3 对数-双曲线模型的提出及分析

3.1 模型的提出

该文根据试验数据的变化趋势提出对数-双曲线模型，硬化阶段采用对数模型，软化阶段采用双曲线模型，公式如下：

(1)

式中:A1、B1为对数模型参数，利用Matlab拟合求得；A2、B2为双曲线模型参数，A2、B2利用Matlab拟合求得；C为双曲线模型调整值；τ为剪切应力；δ为剪切位移；δu为模型峰值剪切位移。

3.2 参数C的确定及表达式确定流程

根据双曲线公式：

(2)

(3)

根据试验数据中的软化点与式(3)进行数据拟合，该文以钢-标准砂界面在150 kPa下软化点拟合为例，如图4所示，得到A2、B2，由于模型拟合效果较差，因此引入参数C进行双曲线模型调整。C值的确定步骤如下：① 取试验数据中软化点的剪切位移δi(i=1,2,…,j)代入式(3)解出τi；② 将试验数据中软化点的剪切应力τ真i减去τi得出Ci；③ 取均值得到C，公式如下：

(4)

通过参数C的确定及表达式确定流程，确定软化阶段拟合公式的C值，结果如表3所示。

3.3 模型的验证与分析

结构物-标准砂界面剪切应力-剪切位移拟合曲线，如图5所示。该文取硬化阶段对数模型和软化阶段双曲线模型的交点纵坐标作为模型峰值剪切应力，横坐标作为峰值剪切位移，硬化阶段拟合公式、软化阶段拟合公式及相关数据对比如表4所示。

由图5及表4可以看出：① 对于同一结构物-标准砂界面，模型峰值剪切应力随法向应力增大而增加；在同一法向应力下，混凝土-标准砂界面的峰值剪切应力最大，钢-标准砂界面次之，木-标准砂界面最小；② 模型峰值剪切位移在木-标准砂界面和钢-标准砂界面基本呈现出随法向应力增大而增加，但在混凝土-标准砂界面表现不太明显；在同一法向应力下，混凝土-标准砂界面的峰值剪切位移最大，钢-标准砂界面次之，木-标准砂界面最小；③ 通过模型峰值剪切位移与试验峰值剪切位移差值的绝对值|δu-δf|及模型峰值剪切应力与试验峰值剪切应力的比值τu/τf来判断模型的拟合度，可看出|δu-δf|均小于0.21 mm，说明模型对于峰值剪切位移的拟合较好；τu/τf集中在0.96～1.03之间，说明模型对于峰值剪切应力的拟合较好，所以基于试验数据提出和建立的对数-双曲线模型是较合理的。

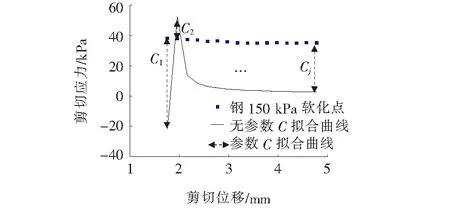
图4 无C及C的介入

表3 软化阶段拟合公式的C值

4 界面数值模拟分析

4.1 数值模型的建立

基于Abaqus模拟软件对结构物-标准砂界面剪切试验进行模拟，界面本构关系采用摩尔-库仑本构模型。模型上部为直径3.09 cm、高度1.25 cm的整体性标准砂模型，标准砂的物理性质与试验标准砂物理性质相同，下部为10.1 cm×9.6 cm×2.5 cm的结构物模型，如图6(a)所示，模型运动状态如图6(b)所示，此次模型共划分单元280个，节点282个。模型分析步采用固定时间增量步长，每级增量步步长为0.08。在界面接触阶段，将室内试验测得的界面摩擦角转化为界面摩擦系数，其中木、钢、混凝土与标准砂的界面摩擦系数分别为0.196 6、0.262 7、0.414 2。在数值模拟过程中固定下部结构物，上部标准砂相对结构物运动，在x轴方向施加1 cm的剪切位移，在法向荷载50、100、150、200 kPa下进行数值模拟。

图5 结构物-标准砂界面剪切应力-剪切

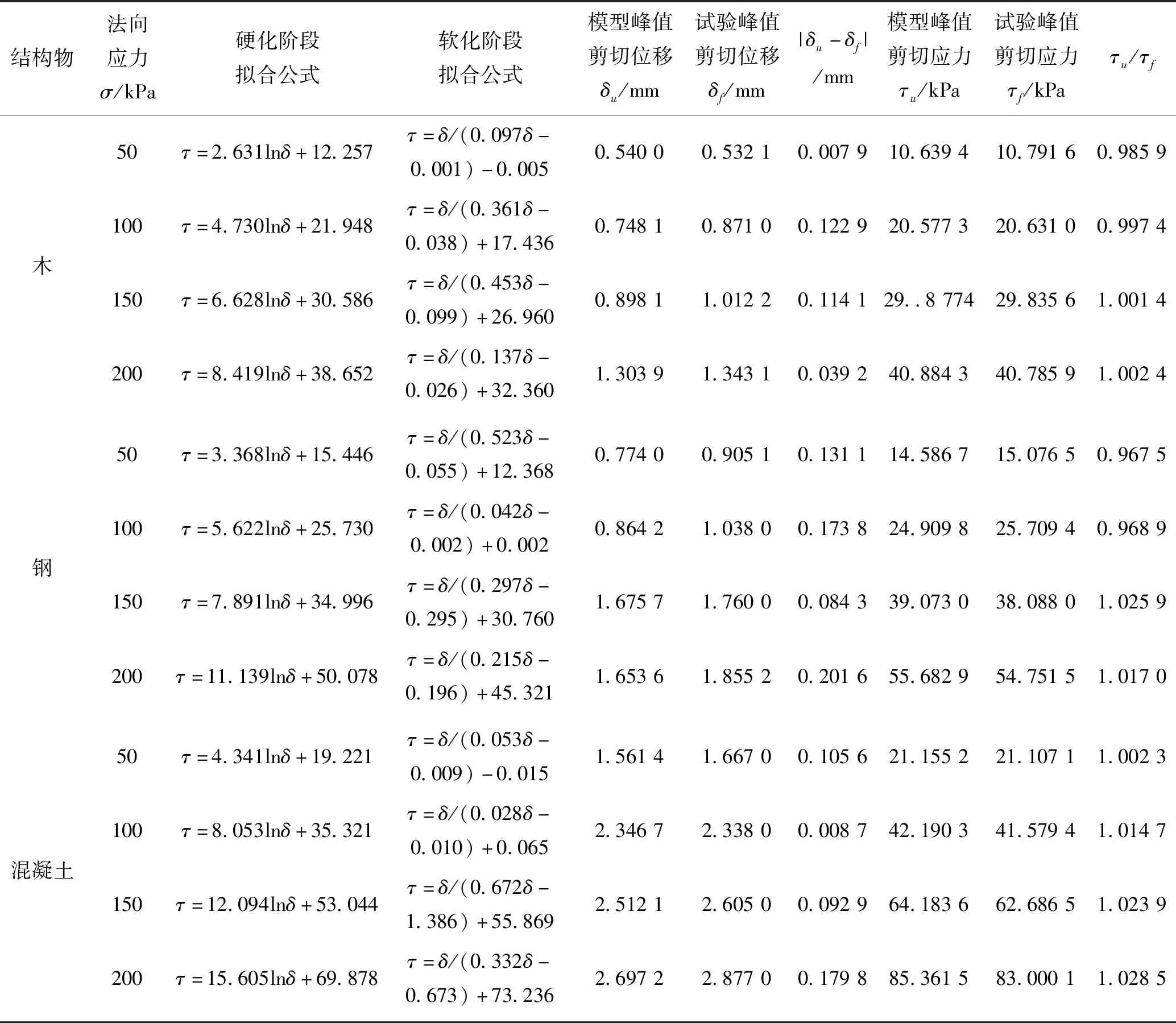
表4 模型公式及相关数据对比

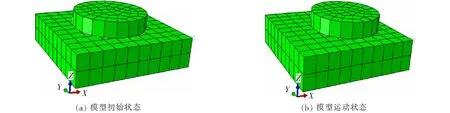
图6 数值模拟模型

4.2 数值模拟结果分析

通过数值模拟得到模拟峰值剪切应力同试验得到的峰值剪切应力进行数据对比，模拟峰值剪切应力用τs表示，如表5所示。

由表5可以看出：① 对于同一结构物-标准砂界面，模拟峰值剪切应力随法向应力的增大而增加；在同一法向应力下，不同界面的模拟峰值剪应力表现不同，木-标准砂界面最小，混凝土-标准砂界面最大，钢-标准砂界面居中；② 通过模拟峰值剪切应力与试验峰值剪切应力比τs/τf来判断数值模型的准确性，τs/τf集中在0.86～1.04之间，木-标准砂界面和混凝土-标准砂界面的τs/τf值大部分在1附近，钢-标准砂界面的τs/τf值在0.87～1.04之间，从拟合效果来看，木-标准砂界面和混凝土-标准砂界面要优于钢-标准砂界面。

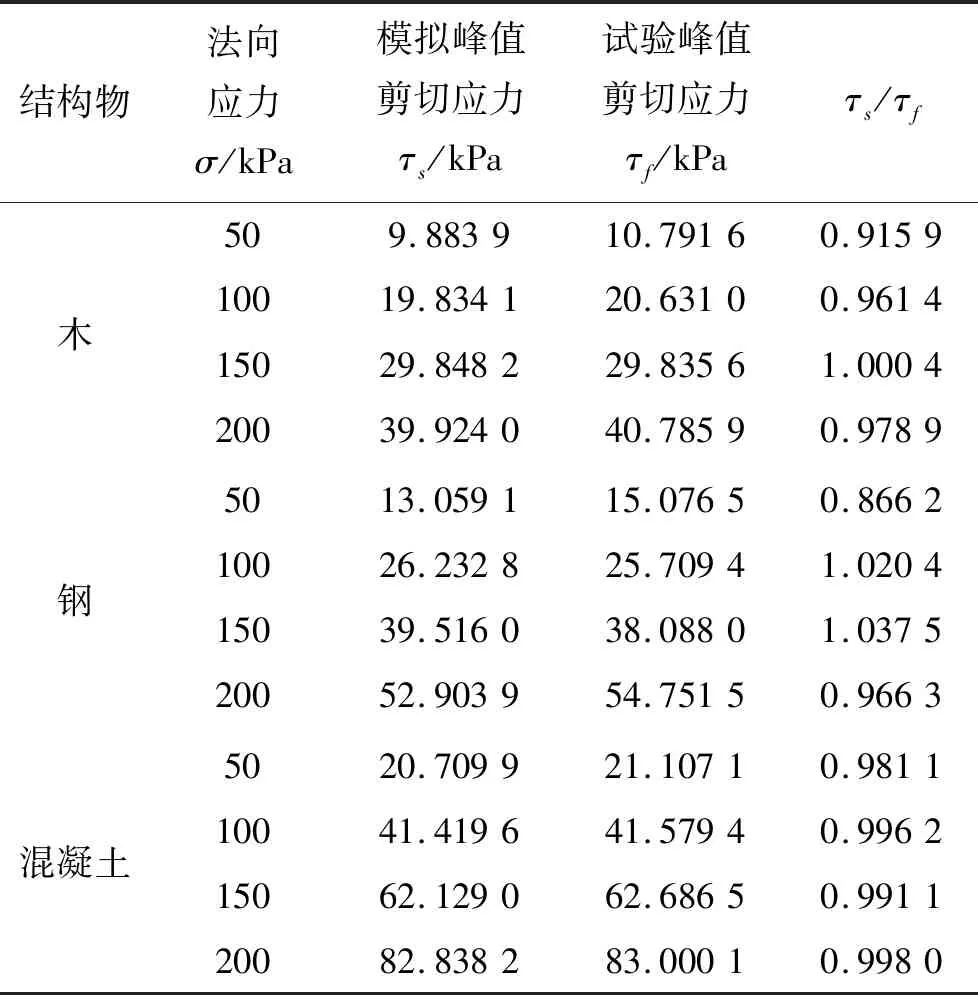
表5 数值模拟数据与试验数据对比

由表5结合表1可以看出：3种界面的模型、模拟、试验峰值剪切应力比较接近，说明数学模型和数值模拟拟合的峰值剪切应力与试验峰值剪切应力比较接近，模拟效果较好。

5 结论

(1) 剪切应力-剪切位移曲线由应力硬化和应力软化两个阶段组成；峰值剪切应力和峰值剪切位移呈现正相关关系，混凝土-标准砂界面最大，钢-标准砂界面次之，木-标准砂界面最小。

(2) 3种界面的表观黏聚力集中在0～1 kPa范围内，差别不大；界面摩擦角差别较大，混凝土-标准砂界面为22.50°，钢-标准砂界面为14.72°，木-标准砂界面为11.22°。

(3) 基于试验数据提出对数-双曲线模型，硬化阶段采用对数模型，软化阶段采用双曲线模型；模型峰值剪切位移与试验峰值剪切位移差值的绝对值|δu-δf|均小于0.21 mm，模型峰值剪切应力与试验峰值剪切应力的比值τu/τf集中在0.96～1.03之间，拟合效果良好，模型的提出比较合理。

(4) 模拟峰值剪切应力与试验峰值剪切应力的比值τs/τf集中在0.86～1.04之间，拟合效果较好。