磨课:初中数学课堂教学的实践探索——以“关于函数的销售问题”为例

■刘冬艳

课堂教学是教师教学实践的主要途径。教师要上出适应学情的好课，为课堂注入新的血液，赋予课堂新的生命，就要经历磨课。课堂教学应具有创新性、艺术性，磨课就是课堂教学焕发活力的不竭源泉。课堂教学在集体智慧的推敲中更加完美，教师的专业素养在磨课中也不断提升。2019年5月，笔者参加了泰州市初中数学优质课评比观摩研讨活动，执教的课题是“关于函数的销售问题”，下面谈谈此次磨课的过程与感受。

一、初次备课

教学目标：利用关键词、句，找等量关系或不等量关系；把方程转化为函数；求一次、二次函数的极值。教学重点：利用关键词、句，找等量关系或不等量关系。教学难点：求一次、二次函数的极值。

教学过程：

1.知识回顾，重梳理。

复习回顾一：（1）利润=售价-成本；（2）总成本=单件成本×数量；（3）总销售额=单件售价×销量；（4）总利润=（单件售价-单件进价）×销量。

复习回顾二：

（1）函数的极值。

（2）一次函数：①当k＞0 时，y随x的增大而增大。当x取最小值时，y有最小值；当x取最大值时，y有最大值。②当k＜0 时，y随x的增大而减小。当x取最小值时，y有最大值；当x取最大值时，y有最小值。

2.牛刀小试，巧转化。

牛刀小试：五一期间，某商场计划购进甲、乙两种商品，甲商品每件进价30元，乙商品每件进价70 元。商场决定甲商品以每件40 元出售，乙商品以每件90 元出售。为满足市场需求，需购进甲、乙两种商品共100 件。该商场要获利1200元，应如何进货？

团队智慧：请每个小组根据以上实际问题，设计一道用一次函数解决的实际问题。

团队智慧展示：挑选有代表性的小组进行成果展示。

3.中考体验，显身手。

（1）（2017·泰州）怡然美食店的A、B两种菜品，每份成本均为14 元，售价分别为20 元、18元。这两种菜品每天的营业额共为1120 元，总利润为280元。

①该店每天卖出这两种菜品共多少份？

②该店为了增加利润，准备降低A种菜品的售价，同时提高B种菜品的售价。售卖时发现，A种菜品售价每降0.5 元可多卖1 份；B种菜品售价每提高0.5 元就少卖1 份。如果这两种菜品每天销售总份数不变，那么这两种菜品一天的总利润最多是多少？

（2）（2018·扬州）“扬州漆器”名扬天下。某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售y（件）与销售单价x（元）之间存在一次函数关系，如图1所示。

①求y与x之间的函数关系式；

②如果规定每天漆器笔筒的销售量不低于240 件，当销售单价为多少元时，每天获取的利润最大？最大利润是多少？

③该网店店主热心公益事业，决定从每天的销售利润中捐出150 元给希望工程。为了保证捐款后每天剩余利润不低于3600 元，试确定该漆器笔筒销售单价的范围。

4.融会贯通，谈总结。

本节课的收获：（1）掌握的知识技能；（2）掌握的思想方法。

二、磨课

专家和同行对教案提出以下几个问题：

1.教学目标，教学重、难点不准确。

本节课重在引导学生建立函数模型，借助函数模型利用函数的性质解决问题，因此教学目标应更改，教学重、难点应做相应调整。

2.课堂增加第二授课人，实现名师进课堂。

增加环节，播放优秀“泰微课”：讲解无锡市2018年数学中考第25题。此微课引导学生如何利用题目中的关键词、语句，找等量、不等量关系，并利用自变量x的取值范围分类讨论，最后以总结解题方法的形式结束。虽然只有简短的6 分19 秒，但可以实现学生对一次函数的基本知识、技能和常用解题经验及思想方法的整体认知。

3.课堂容量偏小，课堂难度设置偏低。

播放优秀“泰微课”后，增加最值问题，旨在提高学生将表格中蕴含的信息与已知条件融会贯通的能力。通过本环节的训练，学生加深了对自变量的取值范围在最值问题中的重要地位的认识和体会，逐步养成分类讨论的习惯。

4.课堂总结，问题设置要有针对性、实用性。

课堂总结不能只关注学生掌握的知识技能、思想方法，还应关注学生在解决问题过程中的学习体验。学生通过印象深刻的学习体验可以有效躲避易错点。学生在每节课的学习体验中都会有或多或少的困惑，谈谈困惑可以为后续复习与能力提升服务。

三、最终教案

1.教学目标更改为：

（1）感受如何将方程问题转化为函数问题。

（2）感受建立一次或二次函数模型解决问题的必要性。

（3）借助函数及其图像解决实际问题，感悟数形结合、函数建模、分类讨论、转化、方程等数学思想。

2.教学重点更改为：结合实际问题建立一次或二次函数模型。

3.教学难点更改为：如何建立函数模型。

设计说明：中考数学复习课重在促进学生数学核心素养的发展，引导学生从更高的视角看问题，以便整合零散的、琐碎的问题，从而本质地看待所学过的内容。方程、函数是初中代数领域的主要数学模型，这些模型有利于学生形成建模的素养。因此本节课的教学目标、重难点应更改为“结合实际问题建立一次或二次函数模型”“如何建立函数模型”。数学建模中，“建”的过程比“用”更重要。

4.增加“名师授课提素养”教学环节，课堂增加第二授课人，实现名师进课堂。

播放优秀“泰微课”——解答无锡市2018 年数学中考第25 题：一水果店是A酒店某种水果的唯一供货商，水果店根据该酒店以往每月的需求情况，本月初专门为他们准备了2600kg 的这种水果。已知水果店每售出1kg 该水果可获利润10 元，未售出的部分每千克将亏损6 元。以x（单位：kg，2000≤x≤3000）表示A酒店本月对这种水果的需求量，y（元）表示水果店销售这批水果所获得的利润。

（1）求y关于x的函数表达式；

（2）问：当A酒店本月对这种水果的需求量如何时，该水果店销售这批水果所获的利润不少于22000元？

设计说明：“微课”作为一种新的教学形式走进课堂，具有形式“微”、内容“精”、整体“妙”等特点。虽然只解决一个或两个问题，但它短小精悍，就像是课堂教学这盘知识大餐的招牌菜，学生可品尝到泰州名师烧出的各种知识美味，数学课堂也因“泰微课”的出现丰满起来。

5.增加“泰微课”的配套练习（连云港市2018年数学中考第24题）：

某村在推进美丽乡村活动中，决定建设幸福广场，计划铺设相同大小规格的红色和蓝色地砖。经过调查，获取信息如下：

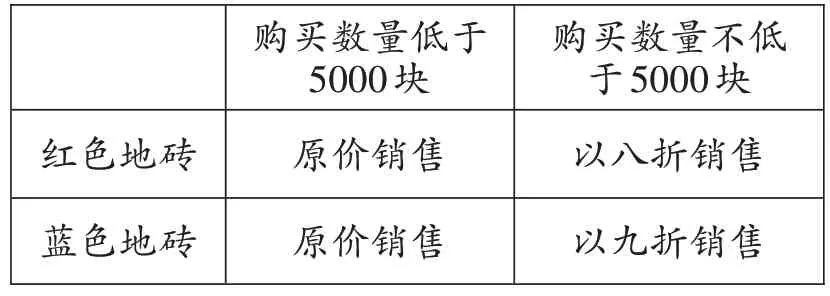
红色地砖蓝色地砖购买数量不低于5000块以八折销售以九折销售购买数量低于5000块原价销售原价销售

如果购买红色地砖4000 块，蓝色地砖6000块，需付款86000 元；如果购买红色地砖10000块，蓝色地砖3500块，需付款99000元。

（1）红色地砖与蓝色地砖的单价各多少元？

（2）经过测算，需要购置地砖12000 块，其中蓝色地砖的数量不少于红色地砖的一半，并且不超过6000块，如何购买付款最少？请说明理由。

设计说明：“泰微课”的讲解实际上是以点带面，从而唤醒学生对解题策略的思考，充分满足学生尝试用“模式识别”解答中考题的兴趣。教师要引导学生在“模式识别”的过程中，注意运用分类讨论、转化与化归的数学思想对模式加以重组。中考复习，解题教学不仅要引导学生梳理旧知，形成网络，更要引导学生在解题过程中积累经验，最终提高学生分析问题、解决问题的能力。

6.课堂总结更改为：

（1）如何结合实际问题建立一次或二次函数模型？需要注意什么？（2）本节课你学到了哪些数学思想方法？（3）本节课你有哪些学习体验？关于方程、函数的销售问题，你还存在哪些困惑？

设计说明：课堂总结既要关注学生掌握的知识技能、思想方法，还应关注学生在解决问题过程中的学习体验，通过印象深刻的学习体验可以有效躲避易错点。

四、磨课效果及反思

增加“名师授课提素养”教学环节后，学生对新型的教学形式充满好奇，在好奇心的驱动下，对“泰微课”配套练习产生了浓厚的兴趣。通过小组合作交流，学生尝试从已有的学习经验出发，先进行“模式识别”，再类比学习名师讲授的数学模型，寻找数学知识之间的内在联系。虽然配套练习具有挑战性，但学生很享受建立数学模型并求解的学习体验。这个教学环节的增加不仅提高了学生解决问题的能力，还给予学生解决问题的钥匙。

课堂总结对于数学课堂而言就是“收口”“点睛”的优化作用。更改后的课堂总结不仅可以帮助学生形成完整的知识体系，深化学生的思维水平，还能培养学生积累学习体验、善于提出问题的良好习惯，提高了学生的数学核心素养。