考虑拥堵区域的多车型绿色车辆路径问题优化

赵志学，李夏苗，周鲜成

（1. 中南大学交通运输工程学院，长沙410083； 2. 移动商务智能湖南省重点实验室（湖南工商大学），长沙410205）

（*通信作者电子邮箱zhaozhixue90@126.com）

0 引言

近年来，节能减排热点问题引起了世界各国的密切关注。在哥本哈根举行的联合国气候大会上，中国承诺到2020 年将单位GDP（Gross Domestic Product）的碳排放量减少到2005 年水平的50%～60%。在全球碳排放统计中，整个交通运输部门占14%，而公路运输碳排放占整个交通部门碳排放量的70%以上［1］。实施绿色运输已经成为当今社会节能减排的必然趋势，倡导绿色发展，以降低能耗、减少碳排放为目标的绿色车辆路径问题已然成为学术界研究的热点。Bektaş 等［2］对传统车辆路径问题（Vehicle Routing Problem，VRP）的目标进行扩展，提出污染路径问题，其优化目标不仅考虑车辆使用成本，同时也考虑车辆的油耗和碳排放。Demiraab 等［3］、Demir等［4-·5］等 对 对 绿 色 车 辆 路 径 问 题 进 行 了 评 述；Kara 等［6］、Tarantilis 等［7］、李进等［8］、陈玉光等［9］、吴丽荣等［10］分别以最小化油耗、最短行驶距离、最小化租车费用以及准时送货为优化目标建立绿色车辆路径模型（Green Vehicle Routing Problem，GVRP），并分别采用改进的粒子群算法、基于模拟退火和禁忌搜索的两阶段求解方法以及基于路径划分的禁忌搜索算法进行求解。Xiao 等［11］、Zhang 等［12］、葛显龙等［13］构建了不同目标下的低碳低油耗的绿色车辆路径问题，并分别采用模拟退火算法、混合人工蜂群算法、改进的粒子群算法和遗传算法进行求解。在油耗和碳排放测度研究中，Demir等［14］和Suzuki［15］研究表明车速、载重、道路坡度和交通拥堵是影响油耗最重要的因素，Kuo［16］、Maden 等［17］研究表明道路拥堵对油耗和碳排放将产生重要影响，随着拥堵程度的增加，油耗和碳排放量将显著增加。Tarantilis 等［18］以希腊肉类和牛奶的配送为例，研究了多车型、多配送中心的开放冷链物流配送车辆路径问题，并采用门槛值法进行求解；Amorim 等［19］针对葡萄牙一个食品配送问题构建了多时间窗多车型车辆路径问题。何东东等［20］研究在传统带时间窗车辆路径问题（Vehicle Routing Problem with Time Window，VRPTW）的基础上，从节能减排的角度出发，引入了油耗和碳排放量的近似计算方法，建立了带时间窗且考虑低碳和成本节约的多车型绿色车辆路径问题模型，并设计了改进的禁忌搜索算法求解该问题。

综上所述，关于绿色车辆路径问题的研究已经产生一定的研究成果，但也存在一定的局限性，主要体现在以下三个方面:1）对客户分布在交通拥堵状况不同的区域，其绿色车辆路径如何规划缺乏研究；2）对车辆行驶在不同拥堵状况的路段上，其速度变化和载重变化如何影响车辆的能耗和碳排放量缺乏研究；3）城市配送大多选用单车型进行研究，而没有考虑多车型混合配送。

基于此本文研究配送中心采用具有固定车辆数的多种车型，以能耗、碳排放和车辆管理使用成本总成本最小为目标的车辆路径问题，充分考虑城市拥堵状况对车辆油耗和碳排放影响，引入基于车速和载重的油耗和碳排放测度模型，建立了考虑交通拥堵的多车型绿色车辆路径数学规划模型，然后设计了混合差分进化算法求解该问题，将物流管理和能源管理理论有效衔接。

1 问题描述与模型构建

1.1 问题描述

本文研究交通拥堵状况下的多车型物流配送车辆路径问题，可描述为:物流配送中心具有多种类型的车辆，给位于城市不同区域的客户配送货物；客户点的货物需求量确定，具有时间窗要求；客户点的位置已知，拥堵区域已知，交通拥堵状况会影响车辆的行驶速度。目标是在考虑车辆油耗、碳排放和车辆使用成本的情况下，找出满足客户货物需求和时间窗要求的车辆调度和路径安排方案。

为便于分析和研究，做出如下假设:1）配送中心和客户点的位置已知，车辆从配送中心出发，完成配送任务后返回配送中心；2）配送中心具有多种类型的配送车辆，不同类型车辆的数量有限；3）车辆行驶在城市拥堵区域和非交通拥堵的路段上，其行驶速度不同；4）每位客户的货物需求量确定，均小于车辆的最大负载能力，且有服务时间窗要求，车辆可提前到达，但是要承担惩罚费用，但不能超过客户点最迟服务时间；5）每辆车运载的货物重量不能超过其最大负载能力；6）每位客户有且仅有一辆车为其提供配送服务；7）不同类型车辆的单位时间租用费用和固定发车费用不同，车辆租用费用包括车辆使用费和驾驶员工资，根据车辆配送时间进行计算；8）不同类型车辆，单位油耗的行驶距离不同；9）车辆在客户点等待和服务期间，发动机关闭，车辆没有油耗和碳排放。

1.2 符号和变量

G=(N，R)为配送网络；N表示节点集，N={0，1，…，n}，其中0表示配送中心，其余节点为客户点N′；N′ =N{0}。

R为连接顶点的弧集，R={(i，j)|i，j∈N，i≠j}，dij为任意节点i到j的距离。

C为交通拥堵区域，Cˉ为非交通拥堵区域。

m表示车辆的类型，m={1，2，…，M}；k表示车辆的编号，k={1，2，…，K}。

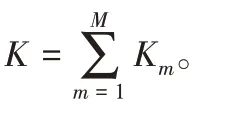
Qm为m类型车辆的容量，m={1，2，…，M}。

qi为客户i的货物需求量（q0= 0）；［ETi，LT］i表示客户i的时间窗要求；为m类型车辆k到达客户i的时间；si为给客户i配送货物的服务时间，Fc表示总的油耗，为m类型车 辆k在路段Rij上的油耗。

E表示总的碳排放量，为m类型车辆k在路段Rij上的碳排放。

TT表示总的配送时间。

ξm为m类型车辆的固定发车费用。

μm为m类型车辆单位时间租用费用。

pm为租用m类型车辆单位时间人力成本。

λf为单位油耗费用。

λe为单位碳排放费用。

2 模型建立

2.1 考虑交通拥堵区域描述以及行驶时间计算

为了更好地描述实际城市拥堵状况，本文采用文献［21］方法，利用交通拥堵圆形（Congestion Circle，CC）区域模拟城市拥堵状况。设以城市中心点为圆心，r为半径的圆形区域作为城市拥堵区域，其余为非拥堵区域，拥堵区域内所有路段均为拥堵路段，车辆在该路段内均以拥堵车速vc行驶，车辆在非拥堵区域内陆段以vf行驶。行驶随着时间变化，拥堵区域半径r和拥堵车速随之变化。如Rij在城市拥堵区域内，存在交通拥堵状况，车辆以拥堵速度vc行驶，车速较慢，其行驶时间为dij vc；如果Rij在非拥堵区域内，车辆以正常速度vf行驶，车速较快，其行驶时间为dij vf；如行驶路段跨越了拥堵区和非拥堵区，则其行驶时间由行驶在交通拥堵路段Rij1上的时间和非拥堵路段Rij2上的时间两部分构成，车辆行驶的具体情况如图1。车辆行驶在Rij时间tij的计算如式（1）所示。通过行驶路线（以两节点之间的线段）与拥堵区域（圆形区域）之间的位置关系判断拥堵路段和非拥堵路段长度进而求解行驶时间。

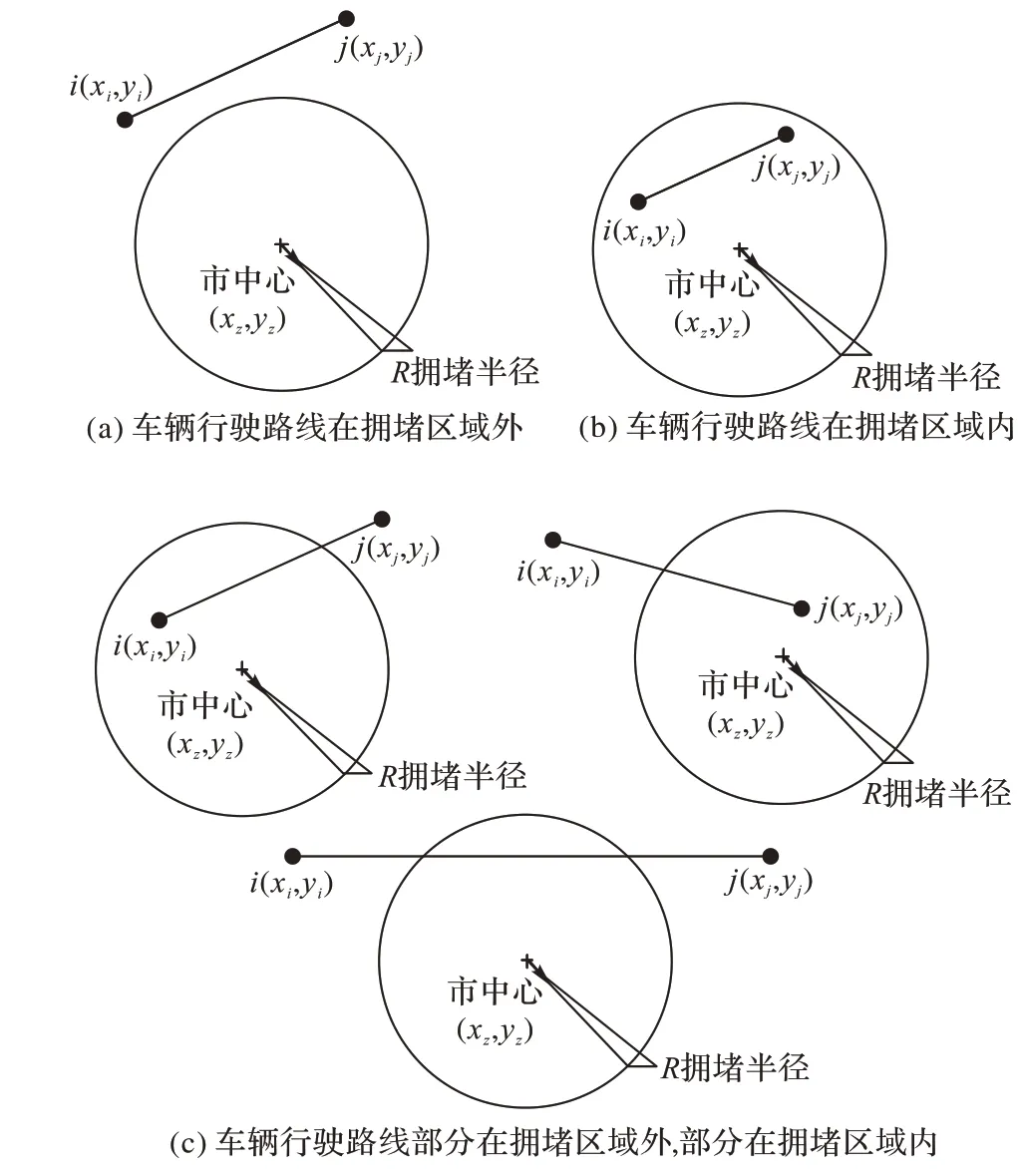
图1 考虑拥堵区域的车辆行驶路线Fig 1 Vehicle routes considering traffic congestion areas

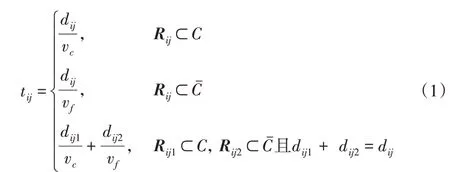
其中:C为拥堵区域，Cˉ为非拥堵区域。

2.2 需求点时间窗处理

由于客户对收货时间有着严格的要求，要求配送车辆必须在规定好的时间窗内到达，但是由于道路拥堵和车辆调度的原因，配送车辆往往不能准时到达，这就予以一定惩罚，因此惩罚费用成本Pi为:

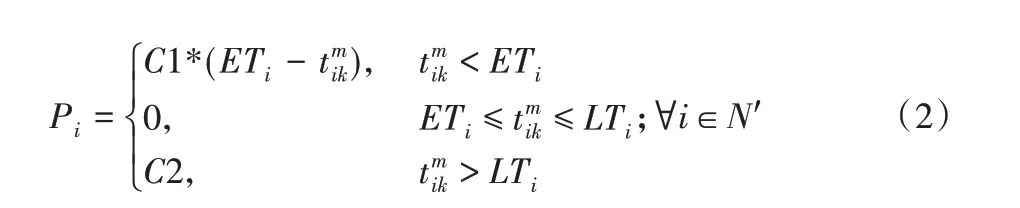
时间窗约束允许车辆到达时间早于ETi，则等待时间为，但到达时间早于时间窗则需要承担一定的惩罚费用，C1是惩罚因子，C2为非常大的正数。

2.3 油耗与碳排放计算

油耗和碳排放受多种因素影响，其中速度和载重是两个最重要的影响因素。根据文献［22］，MEET（Methodology for calculating Transport Emissions and Energy consumption）碳排放率估计函数:

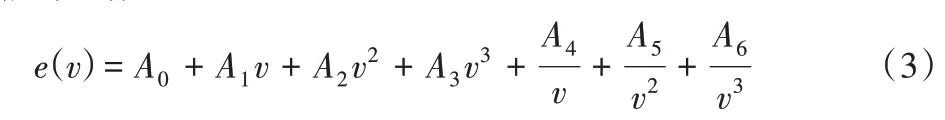
其中:e(v)为空载车辆在坡度为0 的道路上行驶的碳排放率（单位g/km），v表示车速，根据不同拥堵状况车速不同。A0、A1、A2、A3、A4、A5、A6为预定义参数，载重不同的货车取值不同。同时车辆碳排放率还要考虑载重因素进行修正。MEET模型载重修正因子:

其中:γ表示载重率；v表示车速；B0、B1、B2、B3、B4、B5、B6、B7为定义参数，不同车型的货车取值不同。不同车型的货车碳排放率kg/km）为:

根据文献［22］方法，碳排放率可以转换成油耗率，设定1 L 汽油产生2.32 kg 碳排放量，则产生1 kg 碳排放量的油耗为1/2.32=0.431 L。因此不同车型的货车油耗率为:

2.4 模型的构建

在考虑行驶速度、运载量变化影响油耗成本、车载容量约束、时间窗、多车型等情况下，满足所有客户的需求，以油耗和碳排放量最少、车辆使用成本最低为目标，构建双目标优化模型，如下所示:

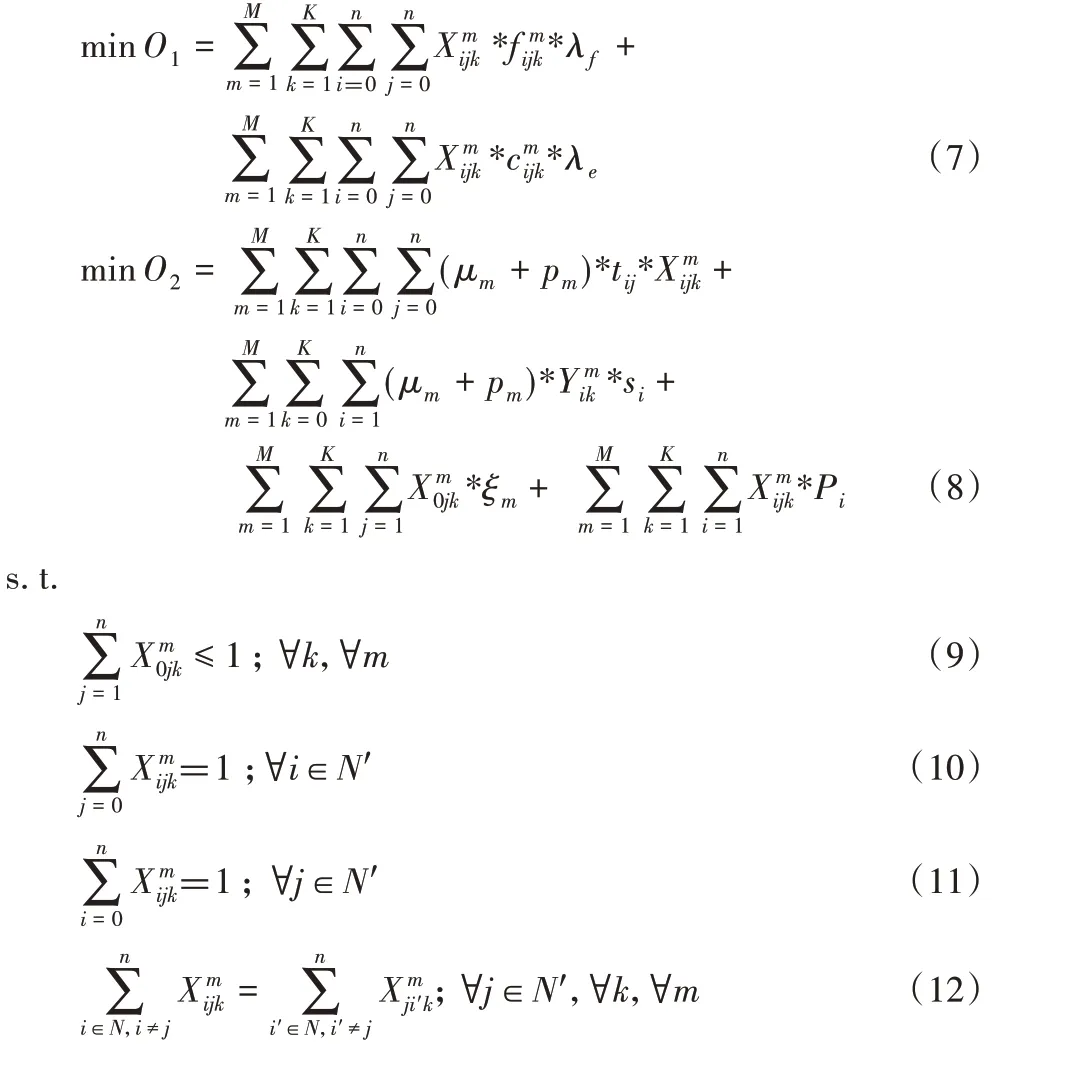
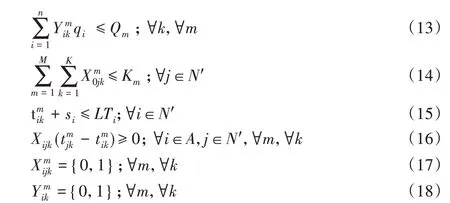
式（7）、（8）表示目标函数，第一个目标表达式表示所有车辆油耗和碳排放的总费用，第二个目标表达式表示车辆管理成本，包括使用的时间成本、人力成本、车辆的固定发车费用，以及时间窗惩罚成本；式（9）表示每辆车只能从配送中心离开一次；式（10）、（11）表示一个客户点只能有一辆车进行配送服务且仅服务一次；式（12）表示进入客户点服务的车辆必须离开客户点；式（13）表示车辆的载重不能超过其容量；式（14）表示每种类型的车辆数约束；式（15）表示时间窗要求；式（16）表示车辆配送的先后顺序；式（17）、（18）表示0-1决策变量。

3 求解模型混合差分进化算法

3.1 混合差分进化算法设计的基本思想

基本差分（Differential Evolution，DE）算法［23-26］是一种基于实数编码的用于连续空间函数的优化进化算法，而本文多车型绿色车辆路径优化问题是一个典型的离散化问题，因此标准DE 算法不能直接应用于本文模型求解。为此本文通过种群结构的修正和操作算子的改进将变异操作后的实数转化为整数，使之能继续进行交叉操作和选择操作，从而使差分进化算法能求解车辆路径这种离散优化问题。

3.2 种群编码和解码

1）种群编码。混合DE算法编码采用如下设计:假设一个配送中心为n个需求点提供配送，其中配送中心可以提供M种类型运输车，运输车数量为K，其中1 至e号车和e+1 至K号车分别为两种不同类型运输车。采用n维实数向量表示粒子的状态，因此个体每一维xj(j= 1，2，…，n)为实数，其范围为（1，K+1）。对n维例子进行解码操作，其中整数部分代表车辆号码，由1-K整数随机构成，整数部分相同的，表示由同一辆车运输，小数部分的大小表示车辆运输需求点的次序。

2）解码说明。按照文献［25］方法，记［x］表示对X取整数部分，具体解码过程如下:

步骤1 对于粒子每一维，进行［x］操作。

步骤2 根据［x］值进行分组，形成车辆分组。

步骤3 在分组内，根据客户点时间窗要求，对同组维数进行排序操作获得车辆配送需求点的次序。

假设7 个客户VRP 问题需要三辆车，具体参数如表1 采用编码方式如下。

表1 编码举例Tab. 1 Code examples

按照上述编码方法解码，1至2号车为一种类型运输车，3号车为另一种类型运输车。将xi（i=1，2，…，7）取整，整数部分相同的分在一组，得到3 组:（4.1），（1.86，1.53，1.12，1.24），（3.29，3.05），将上述状态映射到相应客户点得到:（1），（2，3，4，5），（6，7）；然后根据时间窗要求，客户点最早的服务时间进行排序，如果客户点最早服务时间相同，则比较最晚服务时间。得到相对应的配送路线:第一辆车（0-1-0），第二辆车:（0-2-5-4-3-0），第三辆车（0-6-7-0）通过此种解码，维数和客户点数目相当，使粒子可以进行变异和交叉操作，使差分进化算法能用于求解VRP这种离散优化问题。

3.3 改进差分进化算法设计

步骤1 初始化。参考文献［26］进行基本参数设置，包括:群体规模NC，最大迭代次数Tmax，缩放因子F，交叉概率（Crossover Rate，CR）的上下界CRmin，CRmax，全局最优解为xbest，迭代计数器t= 0，在实数（1，K+1）范围内随机产生一组n维粒子x（i）（i=1，2，…，NC）。

步骤2 构建可行解。初始解或临时种群解码后产生的线路，可能会发生客户的需求量超过车的载重或者车辆达到时间超过时间窗的情况发生，从而产生非法解。为了减少或者避免这些情况的发生，就需要对种群结构进行调整，从而产生可行解。首先要对每条线路的载重和客户进行评估，然后通过启发式算法进行调整。本模型使用节约法和最邻近法对线路内核线路间的客户进行调整，一方面对所得结果进行改进，另一方面修正非法解。具体的过程如下所示:

步骤2.1 计算解码后各条线路的负载，并记录。

步骤2.2 对于超重的非法线路，按照顺序从中移除若干客户，使其合法化。将这些客户放入待选客户列表。

步骤2.3 对于线路中客户负载远小于载重的线路，将其线路删除，将客户放入待选客户列表。

步骤2.4 根据启发式算法中最邻近法和节约法，保证线路载重可行的前提下，将待选列表的客户插入已有的线路中。如果已有线路已经饱和，则根据待选客户的最早服务时间作为种子客户初始化一辆车。

步骤2.5 判断待选列表是否所有客户都遍历到，如果待选客户列表还有需求点，继续进行步骤2.4；否则，则转向步骤2.6。

步骤2.6 根据现有的线路情况和客户时间窗要求，进行粒子所代表线路中客户点服务顺序的修正与改进。

步骤3 适应度函数计算。根据式（6）、（7）分别计算目标值O1、O2，令w1、≥0，w2≥0，w1+w2= 1)分别表示O1、O2的权重。因此总的目标函数为fit(x)=O1w1+O2w2，从而获得更优的粒子即更好的行驶路线。

步骤4 变异操作。在混合DE 算法中，将模拟退火算法引入到基本DE算法差分变异操作中，并在交叉操作中引用不变交叉概率因子CR策略［25］。

其中:xat、xbt、xct为互不相同的父代个体，代表父代不同行驶路线，xbestt为种当前迭代次数下种群中适应值最好的个体，FT∈[0，2]为变异因子，ra∈[0，1]，ra=(Tmax-t)/Tmax，利用ra成为退火因子，从而保证算法既有较强的全局搜索能力又有较快的收敛速率和较高的搜索精度。

步骤5 交叉操作。利用交叉操作是为了增加群体的多样性，对于群体中目标矢量个体x（i，:），将与变异矢量uz进行交叉操作，产生探测个体xˉ。为保证个体x（i，:）的进化，首先通过随机选择，使得至少有一位由uz贡献，而对于其他位，可利用一个交叉概率因子CR，决定xˉ中哪位由uz贡献，哪位由x（i，:）贡献。交叉操作的方程为:

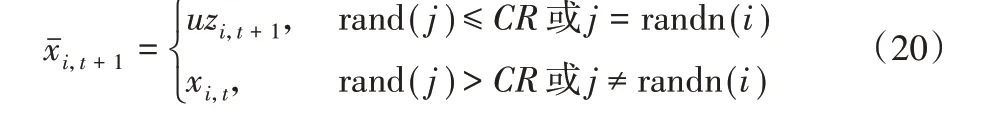
同时采用不变交叉概率因子CR策略。令:

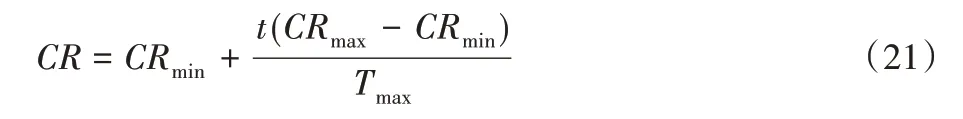
其中:CRmax为最大交叉概率，CRmin为最小交叉概率，再通过步骤2得到临时可行解种群。

步骤6 选择操作。利用“贪婪”选择策略，从种群中父代个体xi，t和实验个体xˉi，l+1中选择生命力最强的作为下一代个体，从而形成新的种群。具体步骤如下:

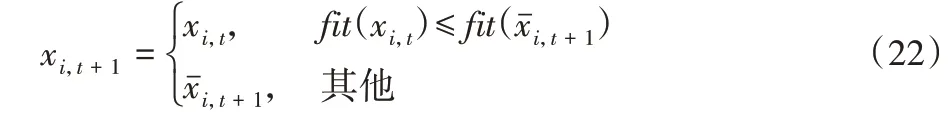
步骤7 算法结束判断。进化代数t=t+1，并记录当前整个群体中最佳个体。如果满足最大迭代数，则终止算法；否则返回步骤4。

4 算例分析

4.1 实验设置

算例采用Solomon 测试数据库中的R208 进行仿真实验，该算例需求点数量为100 个，各需求点服务时间、时间窗、需求量均为算例所述，令1 个重量单位为30 kg。设定配送中心点坐标为（35，35），城市中心坐标为（40，40），初始拥堵区域半径为R=20 km，配送中心具有满载重量分别为4 t和8 t两种不同类型的车辆。根据文献［22］以及目前交通运输市场的情况，各相关数据如表2、表3和表4所示。

表2 碳排放系数Tab. 2 Carbon emission coefficients

表3 载重修正因子系数Tab. 3 Load correction factor coefficients

表4 运输车辆信息Tab.4 Vehicle information

参考碳交易市场的行情，将与有关费用设置如下［27］:λf=7.5 元/L，λe=0.052 8 元/kg，时间窗惩罚系数c1=10 元/分。将上述混合差分进化算法程序在Matlab 7.0 在2.50 GHz CPU和4 GB 内存的微机上进行求解，程序运行参数设置如下:种群规模NC=50，最大迭代次数Tmax=100；最小交叉概率为CRmin= 0.1，最大交叉概率CRmax= 0.9，变异因子FT= 0.5。

4.2 算例仿真结果分析

4.2.1 车辆行驶路径与拥堵区域结果分析

为了更加符合实际，令拥堵区域内车速vc=30 km/h，城市拥堵半径为20 km，并取权重w1=0.8，w2=0.2 进行算例仿真，运行时间为690.4 s。其优化仿真结果见表5。表5 中VN（Vechile Number）表示车辆编号，VT（Vechile Type）表示车辆型号，VR（Vechile Route）表示行车路径，FC（Fuel Cost）表示油耗成本，CC（Carbon Cost）表示碳排放成本，VMC（Vehicle Management Cost）表示车辆使用管理成本，DL（Distance Length）表示行驶距离。由表5 可知:1）不同车型车辆配送的需求点数量存在较大差别，配送数量最多的8 t车型达到19个点，数量最少的8 t车型的只有3个点，而且在固定数量的小型车和中型车情况下，小型车完全使用，中型车未完全使用（10号车未启用），其原因是100 个需求点的时间窗不一样，车辆行驶过程中在满足车载量和最小化适应度函数的同时，尽可能避免错过时间窗而产生的惩罚费用；2）小型车的单位油耗碳排放成本、车辆启用成本和车辆使用成本也低于中型车，因此小型车使用率高于中型车，先尽可能满足小型车配送，然后在满足中型车配送。

4.2.2 不同拥堵程度仿真结果比较

模型的目标函数和其他约束不变，拥堵区域行驶速度vc不同，令w1=0.8，w2=0.2，拥堵半径为20 km，对不同拥堵车速下的仿真结果进行分析，如表6 所示。FCC（Fuel Consumption and Carbon emission cost）表示油耗碳排放成本，TC（Transportation Cost）表 示 总 配 送 成 本，NV（Number of Vehicles）表示车辆使用数量。数据表明:1）随着拥堵区域行驶速度逐渐降低，导致油耗、碳排放的费用逐渐增大，说明油耗和碳排放、车辆使用成本以及总成本与拥堵程度正相关；2）随着拥堵状况严重，拥堵车速减小，行驶距离也随之增大，说明随着拥堵程度的增加，车辆要尽量规避拥堵区域，导致行驶距离随之增大，会对行驶路径产生影响；3）随着拥堵车速减小，为了满足时间窗，就会增加车辆数来满足需求点，说明拥堵状况越差，车辆使用数越多，车辆使用成本提高。

4.2.3 不同拥堵半径仿真结果比较

需求点位置、时间窗和需求量等情况不变，vf=60 km/h，vc=30 km/h，考虑拥堵区域变化情况下分析计算。表7 中，RC（Radius of Congestion）表示拥堵区域半径。由表7 结果可见，随着拥堵区域扩大，车辆使用数量、车辆总行驶距离、车辆油耗和碳排放费用与车辆使用费用都会随之增加。由此可知车辆使用成本与拥堵半径正相关，尤其在拥堵半径最大时也就是拥堵区域最大时总成本最大，油耗和碳排放也是最多。

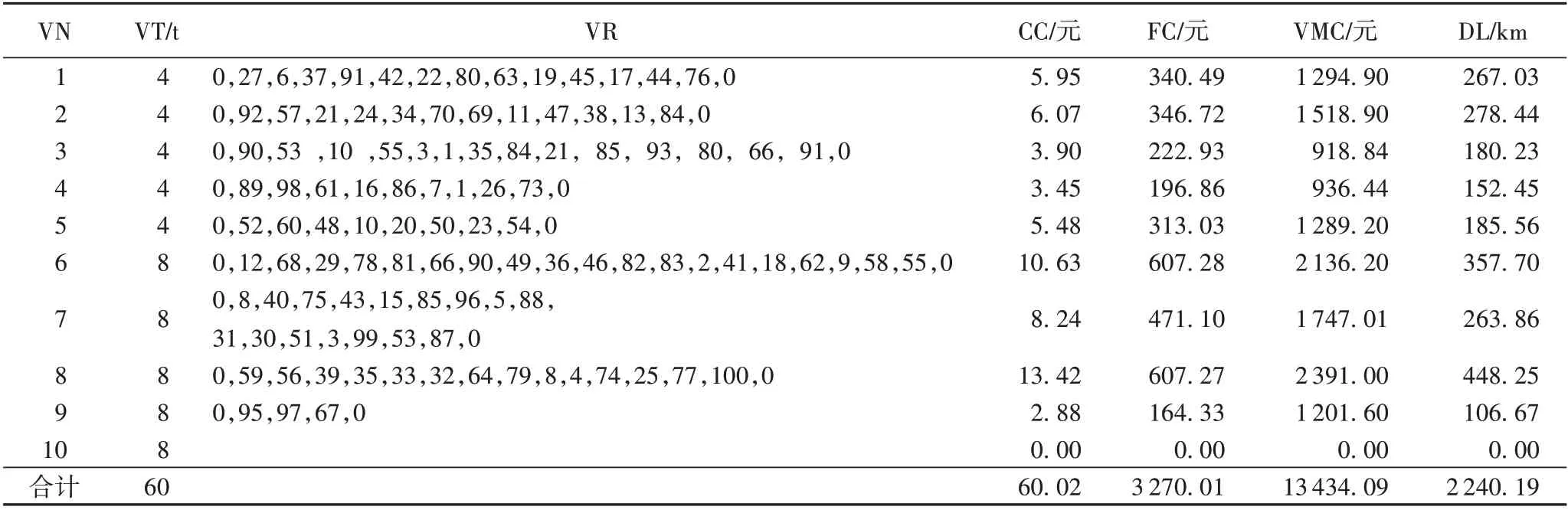
表5 算例R208车辆在拥堵车速vc=30 km/h下的行驶路径方案明细表Tab. 5 Driving path scheme of the example R208 vehicles at vc=30 km/h in traffic congestion area

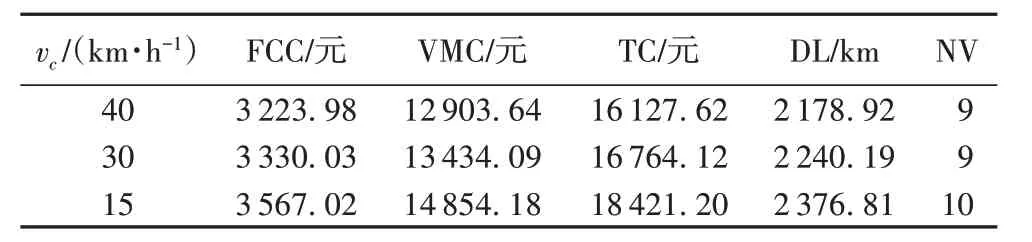
表6 不同拥堵车速状况下行驶路径与相关费用表Tab.6 Driving paths and related costs with different speeds in traffic congestion area

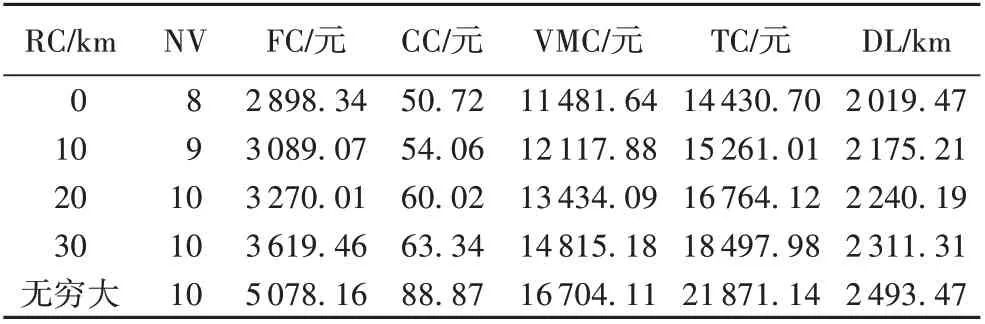
表7 不同拥堵区域情况下数据分析Tab.7 Data statistics under different congestion area situations

4.2.4 不同权重组合的仿真结果比较

在其他变量参数不变的情况下，令vf=60 km/h，vc=30 km/h，拥堵半径为20 km，将油耗与碳排放费用与车辆使用费用的权重w1、w2分别不同取值，w1+w2=1，w1＜1，w2＜1，w1＞w2。计算结果如表8所示。由表8可知，配送总成本费用主要由油耗碳排放费用和车辆使用成本费用组成，而且车辆使用成本占总成本的很大比例，这说明:1）物流配送成本主要来自车辆使用成本，要降低物流配送成本，就要尽可能降低车辆管理使用费用。2）油耗碳排放费用占总成本费用比例偏低，最高也只达到20%，其中碳排放费用占总成本的比例更是微乎其微，物流企业因此不会太注意碳排放成本。3）当w1、w2均为0.5时，车辆使用成本最低，油耗和碳排放费用最高。随着w1上升，w2下降，油耗和碳排放费用逐渐降低，车辆使用成本升高，但是车辆总成本随之增大。说明如果加大对绿色路径的优化，就必须强调节能减排，导致物流配送成本增加。

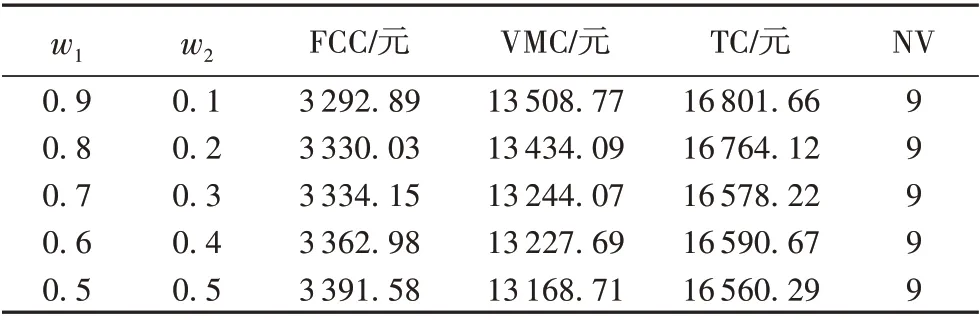
表8 不同权重仿真结果比较Tab.8 Comparison of simulation results with different weights

4.2.5 不同优化目标仿真结果比较

在算法程序其他条件不变的前提下，令vf=60 km/h，vc=30 km/h，分别以总油耗和碳排放费用、车辆总行驶距离、车辆总运行时间作为优化目标，对算例R208进行仿真实验，具体结果见表9，其中VTT（Vehicle Travel Time）表示车辆运行时间。由表9 可知:1）以油耗和碳排放为优化目标时，油耗与碳排放费用最小；以行驶距离最短为目标时，行驶距离最小；以运行时间最小为目标时，车辆运行时间最小；本文提出的优化目标，总成本和车辆使用成本最小。2）以油耗与碳排放费用、车辆运行时间、行驶距离最小等作为单一目标时，虽然单一目标会达到最优，但会导致车辆数增加、拥堵区域行驶距离增大，客户点时间窗惩罚值增大等情况发生，从而车辆使用成本、总成本大幅度增加，如本文目标与车辆运行时间最短为目标时相比总成本降低了1.2%；与运行距离最短为目标时相比总成本降低了8.1%；与油耗和碳排放最低为目标时相比降低了3.0%。虽然本文模型以油耗与碳排放费用、车辆使用成本作为目标函数，在行驶距离、运行时间、油耗与碳排放费用单项目标不是最优，但总配送成本最低，因此可以获得良好的经济效益。

表9 不同优化目标的仿真结果比较Tab.9 Comparison of simulation results with different optimization objectives

4.2.6 不同车型数量仿真结果比较

本文采用固定数量的不同车型的运输车辆进行配送，同样针对算例R208，分别采用4 t和8 t单一车型进行仿真实验，计算结果见表10。由表10 可知:1）当以4 t 车辆进行配送时，车辆数会增加，从而车辆行驶距离和使用成本会增大，导致总配送成本增大。2）以8 t车辆配送时，车辆数和行驶距离会减小，但是车辆使用成本会加大，从而导致配送总成本增大。3）多车型配送相比单车型配送，相比单一4 t 车型，总成本降低了1.5%，油耗碳排放费用降低了4.3%，说明多车型配送更能节省物流成本。

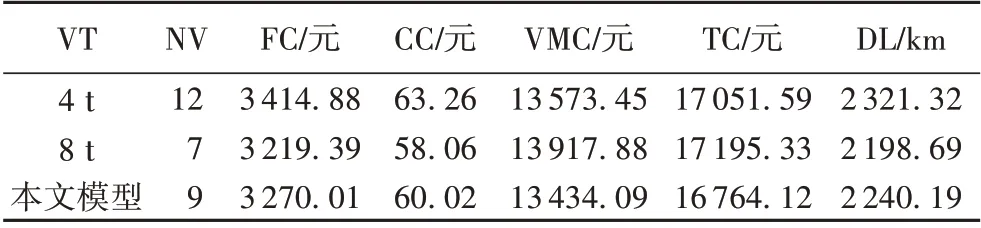
表10 采用单一车型仿真结果比较Tab.10 Comparison of single vehicle simulation results

4.2.7 不同客户分布算例仿真结果比较

为验证本文模型的有效性和正确性，采用多类型算例实验，实验算例R203、R204 的客户坐标属于随机分布，C103、C104 属于集中分布，RC203、RC204 属于混合分布，R 类、RC类分布分配4 t 和8 t 车辆各8 辆配送，C 类分布分配4 t 和8 t车辆各13 辆配送，城市中心坐标均为（50，50），拥堵区域半径为R=20 km，拥堵区域车速为vc=30 km/h，w1=0.5，w2=0.5。实验结果如表11所示，VU（Vehicle Usage）表示车辆使用情况。

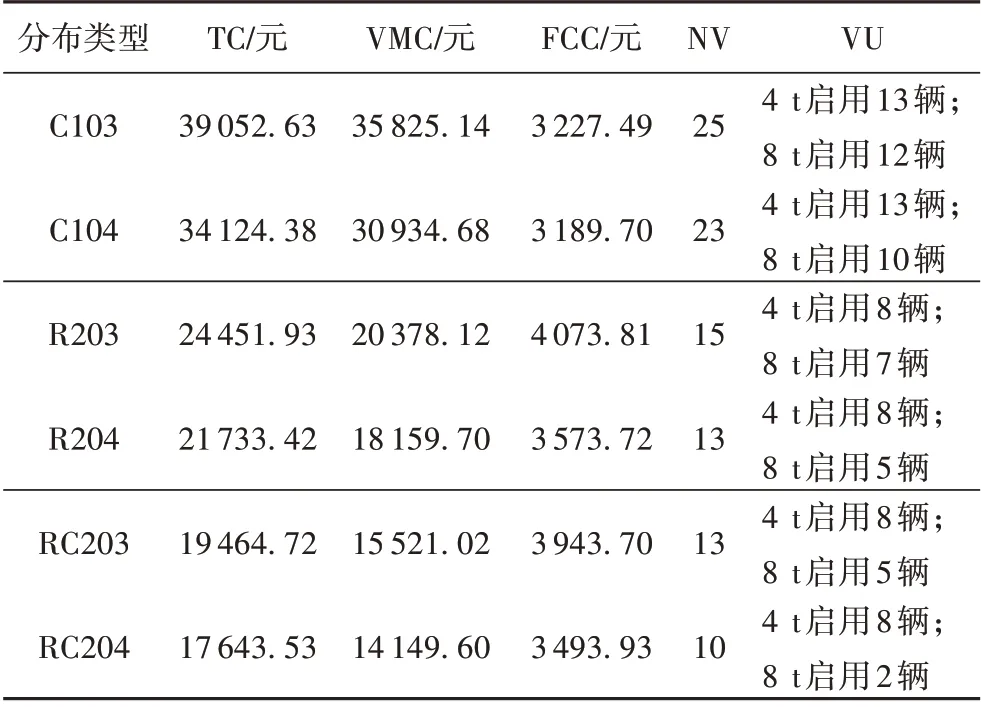
表11 三种不同客户分布算例计算结果Tab.11 Calculation results of examples ofthree types of user distributions

由表11可以看出:1）C类算例的总配送费用、车辆使用和人力成本、车辆使用数量在所有类型中最高，但是油耗成本相比其他类型最低。主要由于C类分布客户点主要集中分布在几个区域，行驶距离较短，因此油耗成本相对较低；但是客户时间窗相对较窄，由于Solomon数据库中C类模型中客户点服务时间为90 min，不同于R 和RC 类客户10 min 服务时间，使得对车辆到达客户点满足其时间窗要求较高，因此车辆只能服务较少客户，但是总的配送行驶时间较长。2）R 类和RC 类总配送费用、车辆使用管理成本、车辆数均小于C 类，主要由于这两种类型服务时间只有10 min，客户均随机分布，客户时间窗要求相对宽松，使得车辆可以配送多个客户，而且总行驶时间较短。3）配送总成本构成中，所有类型的VMC 占比相对较高，均达到80%左右，而C 类占比将近90%，说明物流配送成本主要来自车辆使用管理费用，而这些主要影响因素就是行驶时间，因此要降低物流成本，最主要就是降低总的运输时间。

4.2.8 不同算法算例仿真结果比较

将本文算法与基本差分算法［23］、遗传算法［28］对比实验，算例选取4.2.7 节中三种分布算例，实验参数不变，实验结果如表12 所示。由表12 可知:1）关于C 类型算例，本文差分算法要优于遗传算法和基本差分算法。总配送费用相比遗传算法降低了4.9%，车辆使用数节约了2 辆，相比基本差分算法降低了3.1%，车辆数减少了1 辆；2）关于R 类型算例，本文差分算法有明显优越性。总配送费用降低了9.1%，车辆使用数节约了3辆；相比基本差分算法降低了5.2%，车辆数减少了2辆；3）关于RC 类型算例，本文差分算法有显著优越性。总配送费用降低了11.1%，车辆使用数节约了3 辆；相比基本差分算法降低了6.0%，车辆数减少了2 辆。综上所述本文差分算法更优。

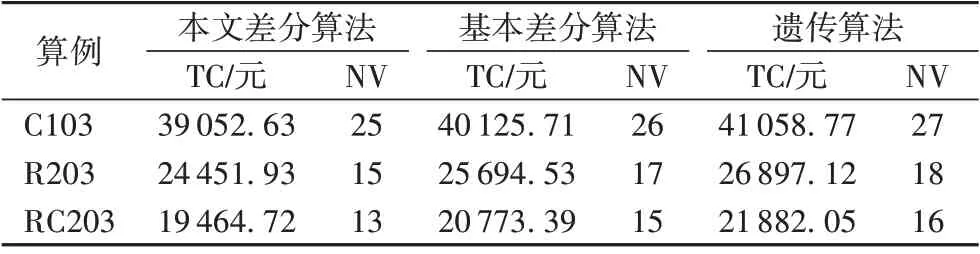
表12 不同算法求解不同算例计算结果Tab.12 Calculation results of different types of examples solved by different algorithms

5 结语

本文以传统的车辆路径问题为基础，考虑了城市拥堵状况，引入基于车速和载重的油耗碳排放测度模型，相应设计了混合差分进化模型进行求解，通过数值实验验证了模型和算法的可行性和有效性，其结论主要有:1）日益严重的城市交通拥堵状况增加了物流配送时间，降低了运输效率，增加了能耗和碳排放，对城市环境污染有着重要的影响，凸显了物流配送中考虑交通拥堵的必要性。2）物流企业在调度配送车辆时，采用混合车型配送比单一车型更加节约成本。3）本文构建的模型在油耗碳排放费用、车辆使用成本双目标折中时，物流配送总成本最低。4）目前物流配送成本主要是车辆使用管理费用，影响其主要因素就是配送时间，因此要合理规划车辆路径，从而减低总成本。5）本文差分算法能有效降低配送费用、减少车辆使用数。6）目前我国的碳税较低，当前的碳交易价格不会显著影响物流企业车辆配送调度安排，因此政府应该适当调整提高碳税，才能有效地促进运输业的节能减排。

由于水平有限，本文只是研究了静态拥堵状况下的多车型车辆路径，虽然也提到了拥堵区域半径和拥堵车速会随时间变化而变化，但并没有研究时变网络下动态车辆路径问题，而且运输物品也是单一类型，所以研究时变网络下动态多车型绿色车辆路径问题将是下一步研究内容。