拉普拉斯分布下的MMSE谱减语音增强算法

王永彪，张文喜*，王亚慧，孔新新，吕 彤

（1. 中国科学院光电研究院计算光学成像技术重点实验室，北京100094； 2. 中国科学院大学电子电气与通信工程学院，北京100049）

（*通信作者电子邮箱zhangwenxi@aoe.ac.cn）

0 引言

语音信号的采集过程中，会受到外界噪声的干扰，噪声的干扰会降低语音质量，使人耳的听觉体验和计算机对语音的处理效果变差。使用语音增强算法，能够改善带噪语音的质量。语音增强算法主要包括谱减算法［1］、基于统计模型的语音增强算法［2］、基于子空间分解的语音增强算法［3］以及有监督的语音增强算法，如基于神经网络的方法［4］、基于非负矩阵分解的方法［5］等。

谱减算法由于其原理直观，复杂度小，具有易于实现和实时性强的特点，被广泛研究与应用，许多有效的改进算法被提出。谱减过程中会出现负值，一般的方法是将负值整流为0，该方法会导致音乐噪声加剧。将频点的谱下限设置为相邻两帧中该频点的最小值，一定程度上减小了音乐噪声；同时，检测相邻帧的最小值会用到未来的信息，不能满足实时应用的要求。针对此问题，文献［6］中使用过减技术，令带噪信号谱减去噪声谱的过估计，同时将谱下限设为本帧估计噪声谱的极小权值，从而避免使用未来帧的信息，该算法通过调整过减因子与谱下限参数，有效地抑制了噪声，并且减小了音乐噪声产生。过减技术中假定噪声对所有频点有相同大小的影响，因而在整个频谱上使用相同大小的过减因子，但大部分的噪声不具有此性质。文献［7］出非线性谱减算法，令过减因子是频率的函数，对不同频点处的噪声使用不同的增益过减因子，在低信噪比频点处减去较大权重，在高信噪比频点处减去较小权重，该方法中，过减因子是通过实验和拟合函数确定的，这种方式获得的参数不是最优的选择。文献［8］提出最小均方误差（Minimum Mean Square Error，MMSE）谱减算法，在最佳准则下求得最优的过减参数，有较好的语音增强效果，但是仍存在语音失真和残留噪声的问题。

该问题的出现有两个原因:1）MMSE 谱减法使用过减因子，是噪声和语音信号离散傅里叶变换（Discrete-time Fourier Transform，DFT）系数为高斯分布的假设下求得的，而在短时语音帧内，语音信号DFT系数的分布与高斯分布的误差较大，而更加符合拉普拉斯分布［9］；2）该算法基于语音活动检测进行噪声估计，将静音帧判决为噪声，即假定语音间隙为噪声，进而对噪声进行迭代更新，当信噪比低时，声音帧容易被误判为噪声帧，谱减后该帧“清零”，导致语音失真，并且该方法更新噪声估计的能力差，当噪声发生变化时，不能追踪到噪声的变化，会使得语音中残留噪声。

根据存在的问题，本文对MMSE谱减算法进行改进，在语音DFT 系数为拉普拉斯分布的假设下，重新推导过减因子的最优估计，并使用短时对数谱结合谱平坦度的方法进行的噪声估计，在语音不失真的前提下抑制噪声，实现对语音信号的增强。

1 谱减算法的参数估计

MMSE 谱减法是对谱减算法一种改进。谱减算法是基于短时傅里叶变换的频域语音增强算法，需通过傅里叶变换，将时域信号变换到频域进行处理。然而语音信号整体上是非平稳信号，不能直接进行傅里叶变换，但是短时间内语音信号变化较为缓慢，可认为是平稳信号。所以，需要首先对语音信号进行分帧处理，每帧长度约为10～30 ms，谱减算法都是在短时帧的基础上进行的。

谱减的基本思想是:在噪声为加性噪声的假设下，使用带噪语音幅度减去噪声幅度，可得到增强语音的幅度。第m帧的带噪信号表示为语音信号与噪声之和:

其中:ym(n)、xm(n)和dm(n)分别表示第m帧的带噪信号、纯净语音信号和噪声信号的时域表达式。将式（1）进行傅里叶变换，转换到频域:

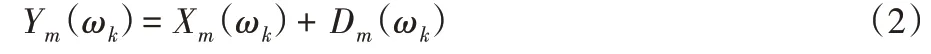
注意到Ym（ωk）、Xm（ωk）和Dm（ωk）是复数，分别表示第m帧的带噪语音、纯净语音和噪声的频域DFT 系数，ωk表示第k个频率单元。

当噪声与语音信号不相关时，式（2）带噪信号、语音信号和噪声有以下关系［10］:

其中:Ym，k、Xm，k和Dm，k分别为Ym(ωk)、Xm(ωk)和Dm(ωk)的模值，表示第m帧的第k个频率分量的带噪语音幅度值、纯净语音幅度值和噪声幅度值，p表示幂指数。

高斯分布下MMSE谱减参数的最佳估计如下。

谱减因子的设置，会很大程度上影响到算法的性能，谱减因子的值过小，对噪声的抑制能力较差；过大会导致语音失真。可通过计算信号DFT系数的分布，在MMSE准则下，求得谱减参数的最优估计［11］。假设纯净语音信号进行离散傅里叶变换之后，其DFT系数的实部和虚部是统计无关的，服从高斯分布。即:

其中:XR(k)= Re{X(ωk)}，XI(k)= Im{X(ωk)}，表示第m帧虚部和实部的方差。

谱减法的一般表达式为:

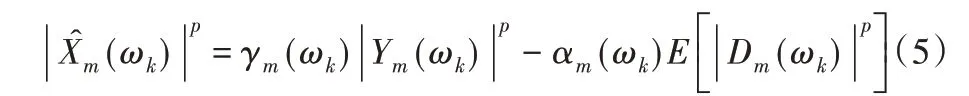
其中，αm(ωk)和γm(ωk)表示谱减参数。当p= 1时是幅度谱减算法，p= 2代表功率谱减算法，p表示谱减算法的阶数。

在MMSE 准则下，基于语音信号服从高斯分布的条件，式（5）中谱减参数的最佳估计为:

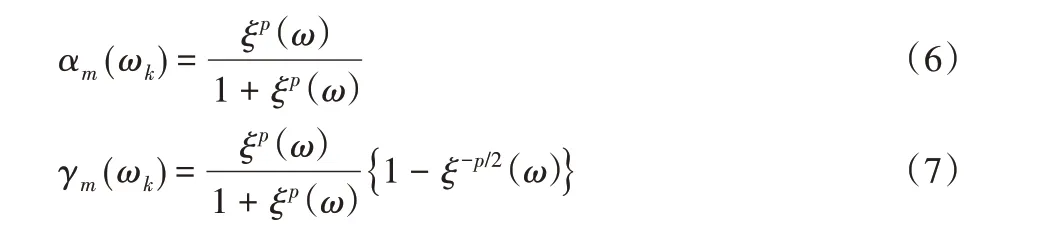
其中:

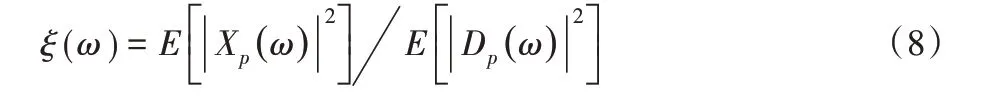
表示本帧带噪语音信号的先验信噪比。

语音信号DFT 系数服从高斯分布的假设，对长时间的语音DFT 系数统计结果是成立的，而谱减算法是在短时语音帧内进行的。在短时帧内，高斯分布的模型与语音DFT 系数的实际分布相差较大，拉普拉斯分布更符合语音的DFT 系数分布。图1 所示分别为长时和短时语音DFT 系数的实际统计分布，以及用统计数据的均值和方差生成的高斯分布和拉普拉斯分布。

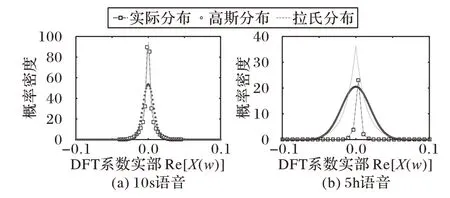
图1 不同时长的语音信号DFT系数统计分布Fig. 1 Statistical distribution of DFT coefficients of speech signals with different time lengths

由图1（a）可以看出，对短时语音帧DFT 系数的统计分布进行近似，拉普拉斯分布的近似效果比高斯分布效果更佳。因此，MMSE 谱减算法中，在计算谱减参数时，运用语音DFT系数服从拉普拉斯分布的假设更为合理，运用高斯分布的假设，会导致谱减参数出现较大的偏差，使用拉普拉斯分布更加合理。

2 改进的MMSE谱减算法

该部分基于语音和噪声DFT系数的实部和虚部服从拉普拉斯分布，推导在MMSE准则下的最佳谱减因子。

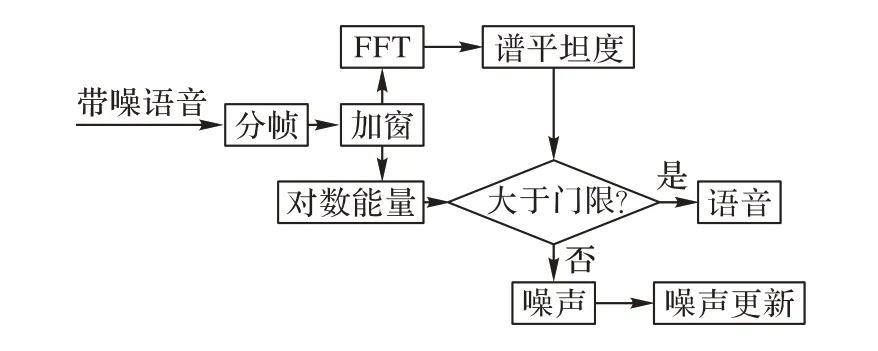
图2 噪声估计算法框图Fig. 2 Block diagram of noise estimation algorithm

根据噪声的幅度谱估计可以得到先验信噪比估计，使用判决引导法进行先验信噪比估计:

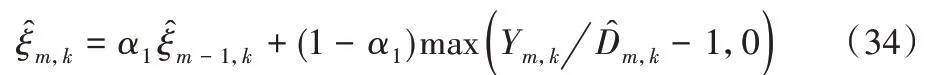
其中:表示先验信噪比估计，α1是权重因子，α1= 0.98 时效果较好。根据拉普拉斯分布的性质，使用先验信噪比估计表示尺度参数平方之比:

通过上述的噪声检测算法，可以实现对噪声的迭代更新。结合对谱减参数的最佳估计，最终得到增强语音。语音增强算法的整体流程如图3所示。

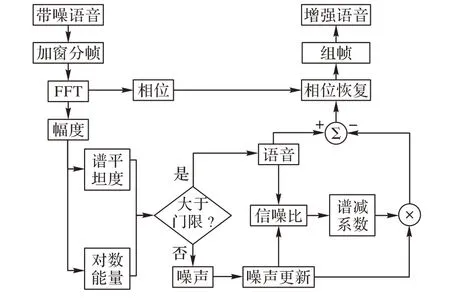
图3 语音增强算法的整体流程Fig. 3 Flow chart of speech enhancement algorithm

3 实验与结果分析

通过仿真实验对算法的增强效果进行验证。选用来源于数据库NOIZEUS 中的纯净语音信号sp01 文件，以及相应的在babble、car和train三种噪声类型下的带噪语音信号，每种类型的带噪信号有四种不同的信噪比，分别为0 dB、5 dB、10 dB 和15 dB。信号的采样频率为8 kHz，量化精度为16 bit。在实验中，语音的帧长为20 ms，使用hamming窗对语音帧进行加窗，帧重叠为50%，算法的幂指数均设为2，即在功率谱下进行谱减。

实验采用信噪比（Signal-to-Noise Ratio，SNR）和语音质量感知评估（Perceptual Evaluation of Speech Quality，PESQ）［16］两种标准对增强语音进行客观评价。PESQ 是2001 年国际电信联 盟（International Telegraph and Telephone Consultative Committee，ITU-T）推出的P.862 标准，PESQ 得分与主观评测相关度较高，是评估语音主观试听感受的客观计算方法，分值区间为-0.5～4.5，得分越高说明语音质量越好。

对带噪语音信号，使用本算法进行增强处理。实验中选用信噪比为5 dB 的Babble 带噪语音信号，时长为3 s。图4 对比了增强前后的语音信号与纯净语音的波形图和语谱图。通过对比可以看出，本文算法能抑制带噪信号中的噪声，对高频处的噪声抑制作用更加明显。

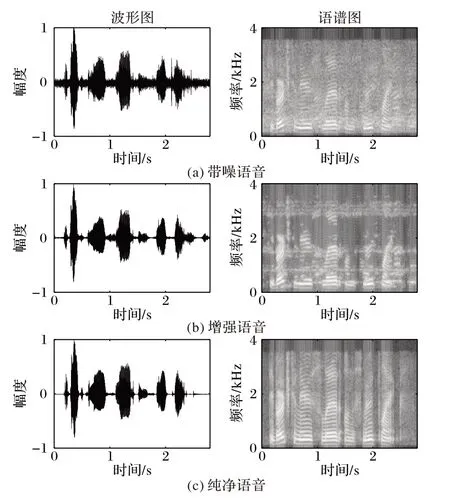
图4 带噪语音、增强语音和纯净语音的波形图与语谱图Fig. 4 Waveforms and spectrograms of noisy，enhanced speech and clear speeches

表1 对比了三种算法处理的增强语音的信噪比。在三种噪声种类下，针对不同信噪比的带噪语音信号使用过减法、MMSE 谱减算法以及本文算法进行增强处理，计算处理后的增强语音信噪比。通过对比可以看出，三种算均能够提高信号的信噪比，可以看出，在信噪比提升能力上，改进算法优于过减法和基于高斯分布的MMSE 谱减算法，说明改进算法对噪声的抑制能力更好。比较算法对不同类型噪声的抑制能力:过减法对不同类型噪声抑制的稳定性差于后两种算法，在Babble 噪声和Train 噪声下，该算法性能较好；而在Car 噪声下，性能较差。对比算法对不同信噪比下的噪声抑制能力:高斯分布下的MMSE谱减法对低信噪比信号的噪声抑制能力差于改进算法。改进算法通过改进的噪声估计方法，能较好地跟踪噪声的变化，对不同类型噪声下的不同信噪比的信号均能提供稳定的噪声抑制能力，能适应不同的噪声环境。

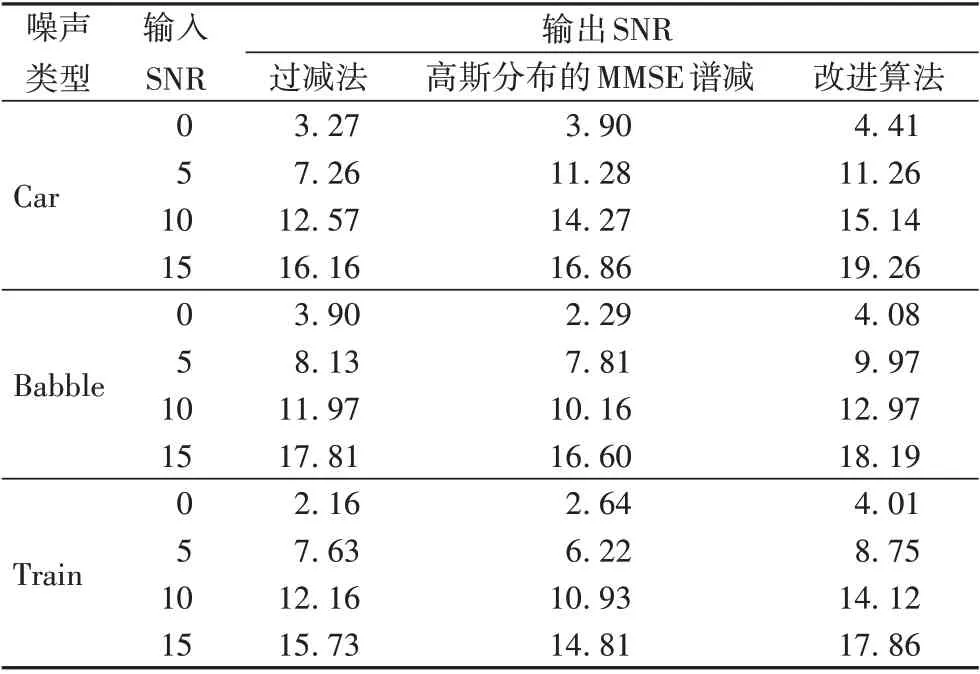
表1 三种算法的输出信噪比对比 单位：dBTab. 1 Comparison of output SNR of three algorithms unit:dB

表2对比了三种算法的PESQ 得分，对于不同噪声类型和不同信噪比的信号，改进算法优于过减法，和高斯分布的MMSE 谱减法性能相当，说明改进算法增强的语音质量更好，造成的语音失真更小。改进算法通过两方面减小语音失真:1）谱减因子的求解是语音信号服从拉普拉斯分布下的假设下求得的MMSE准则下的最佳参数，更加符合真实的语音分布，减小了谱减参数的偏差；2）结合基于对数能量和谱平坦度的噪声估计方法，尽可能避免了语音帧被判别为噪声帧，从而减小增强语音的失真。

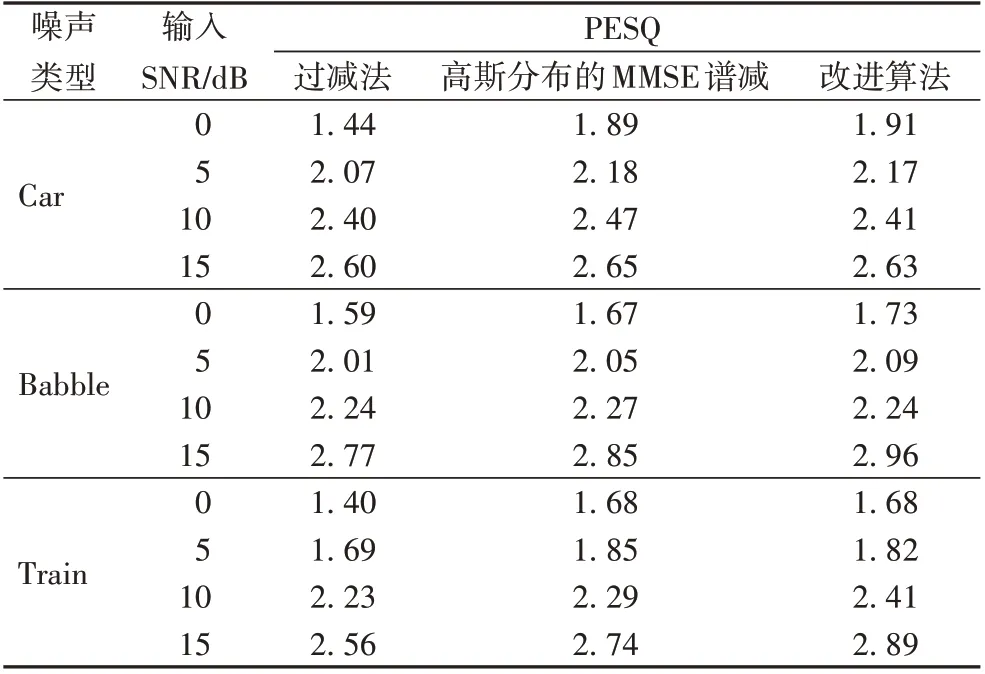
表2 三种算法的PESQ得分对比Tab. 2 Comparison of PESQ score of three algorithms

从增强语音信噪比和PESQ 得分整体来看，过减法可通过增大谱减因子，尽可能地减小噪声，提高增强语音的信噪比，同时由于该谱减参数选择不恰当，导致增强语音出现语音失真。而高斯分布下的MMSE 谱减算法虽然PESQ 得分上优于过减法，和改进算法相当，但是该算法对噪声抑制能力较弱并且对不同噪声抑制的稳定性较差。相比于以上两种算法，本文的改进算法能够在不降低语音质量的前提下，提供更优的噪声抑制能力，实现对带噪语音的增强处理。

4 结语

本文对MMSE谱减法进行改进，将高斯分布的假设改为更加符合实际的拉普拉斯分布，在该假设下求解MMSE准则下最优的谱减系数，并使用短时对数能量结合谱平坦度的方法进行噪声估计，实验结果表明，相比于过减法和高斯分布的MMSE谱减法，改进算法能在语音不失真的前提下，提供更优噪声抑制能力，实现对语音信号的增强处理。语音DFT系数并没有明确的分布，任何分布都是对其的近似，不可避免地出现误差，并且在推导过程中，假设语音DFT 系数的虚部与实部是不相关的，因而两者的相关项为零。而实际中，相关项的期望并不是严格为零的，需要进一步地研究该假设对算法性能的影响。