金属基外延石墨烯相图非谐效应探讨*

高君华，郑瑞伦

(重庆文理学院 电子信息与电气工程学院，重庆市高校新型储能器件及应用工程研究中心，重庆 402160)

0 引 言

固体材料的相变不仅是固体材料的最基本的性质之一，而且是获取各类新材料的重要途径[1,2]。各类相变的条件、特点、遵从的规律是研制各类新材料和应用中需要解决的重要问题，对固体材料相变及其相图的研究，是人们感兴趣的一重要问题。早在上世纪四十年代，为了研究铁磁-顺磁相变，提出了伊辛(Ising)模型和海森堡(Heisenberg)模型；1963年文献[3]发现在NaNO2这种亚铁磁性材料中还出现非谐波效应驱动的拓扑相变。为了从理论上论述固-液-气相变的特点，1980年文献[5]提出二维Colling模型，此后，1983年文献[5]提出了二元合金的二维Bernal晶格模型，用于研究二元合金的结构相变。1996年作者在文献[6]中对二维Bernal模型进一步完善，用它研究了二元合金的的溶解限曲线。2018年Tong等在文献[7]中研究了PbO2中出现的不可约相变。最近文献[8]研究了在锗中的相变。上述研究涉及的均为原子组成结构状态的变化，即结构相变，未深入到原子组成结构不变而电子状态变化的问题。

自2004年石墨烯制备成功以来，由于石墨烯具有优异的电学、力学和热学等性质和二维结构，引起国内外的高度重视并对石墨烯做了不少研究。与单层石墨烯相比，外延石墨烯更与实际接近，研究它的性质更有现实意义，目前已对外延石墨烯的制备和性能进行了大量的研究。除对其制备以及热学、电学性质进行研究外[9-11]，2014年文献[12]和2015年文献[13]对石墨烯在原子组成结构不变而电子状态变化的转变问题进行研究，证明单层石墨烯在考虑到电子自旋后，石墨烯这种由两种子格组成的复式格子，由于原子内部电子相互作用能(内部关联U)和原子间电子相互作用能(外部关联G)的变化，电子系统状态可处于三种状态，石墨烯表现不同的电磁性质：一种是半金属态(PM态)，此状态中每个原子相应于一个具有零自旋磁矩的电子，电子能谱无能隙，材料具有半金属性；第二种是自旋态度波态(BC态)，此状态中原子的电子按子格均匀电荷和自旋分布，两子格电子填充数相等，而自旋磁矩方向相反，系统表现为反铁磁性，电子能谱具有能隙；第三种是电荷密度波状态(BZ态)，这种状态中电子仍按子格非均匀电荷和自旋分布，但两子格电子填充数不等，系统表现为顺磁性。BC态和BZ态是莫特绝缘体，而PM态是半金属。但该文献未对相变的条件、特点作研究，而且单层石墨烯难于实现。2017年Davydov在文献[14]中证明：金属基外延石墨烯中仍存在BC、BZ和PM三态，并研究了这三态的范围，定性讨论了相图的性质。但文中认为原子静止，未考虑到原子作非简谐振动，其结果显示不出温度的影响，不能解释在较宽的温度范围内外延石墨烯存在半金属-反铁磁-顺磁，半金属-绝缘相变的性质。为此，本文考虑原子振动的非简谐效应，建立更完善的物理模型，应用固体物理理论，研究金属基外延石墨烯电磁相变的特点和原子非谐振动对相图的影响。

1 物理模型

我们研究的系统是在金属基底(如Ni)上吸附碳原子形成由A子格和B子格组成的六角形结构的单层外延石墨烯复式格子，最近邻原子间距离为d。取平面为OXY平面，坐标系选取如图1。

A、B子格原子中的电子均具有自旋，自旋为ħ/2的状态用↑表示，而自旋为ħ/2的状态用↓表示。A子格原子中自旋为ħ/2的状态电子填充数记为φ(d)，而自旋为ħ/2的状态填充电子数为δ=d-d0；同样，B子格原子中自旋为ħ/2、-ħ/2的状态填充数为ε0，按照电子填充情况，系统会出现如下3种状态：第一种，A、B子格的原子电子总数相等，但A、B子格原子自旋向上与自旋向下的电子数的差不等，即：ε1、ε2如图2(a),这种状态称为自旋密度波状态(BC)；第二种，A、B子格原子的电子总数不等，但A、B子格原子自旋向上与向下的电子数的差相等，即

图1 金属基外延石墨烯中电子自旋示意图Fig 1 Schematic diagram of electron spin in metal-based epitaxial graphene

nA↑+nA↓≠nB↑+nB↓，

nA↑-nA↓=nB↑-nB↓，

这种状态称为电荷密度波状态(BZ)，如图2(b)所示 ；第三种，A、B子格两种原子的电子数和自旋向下与自旋向下的电子数的差均相等，即

nA↑+nA↓=nB↑+nB↓,

nA↑-nA↓=nB↑-nB↓,

这种状态称为半金属(PM)，如图2(c)所示。

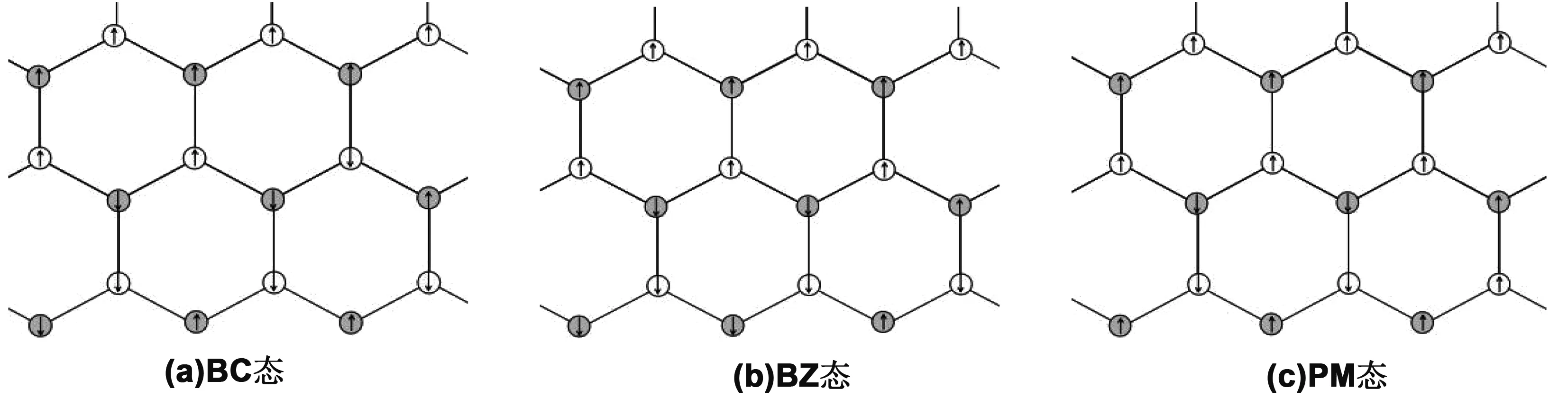
图2 金属基外延石墨烯A、B子格的3种状态的自旋取向Fig 2 Spin orientation of three states of A and B sub-lattices of metal-based epitaxial graphene

为了描述系统状态，引入序参量：a、b、c、d：

(1)

按此定义，a描述总电子数的多少；b描述A、B子格两种原子自旋向上的总电子数与向下总自电子数的差，b>0，表示向上总电子数多于向下得到数；c描述A子格原子与B子格原子的电子数的差，c>0表示A子格原子的电子数多于B子格；d表示A、B子格的自旋向上与向下数目的差异程度，d>0表示A子格原子的自旋向上与向下的差异程度大于B子格。按此理解，BC、BZ和PM的序参量分别是：BC(c=0、d≠0)、BZ(c≠0、d=0)、PM(c=d=0)。

石墨烯原子并不静止，而是作非简谐振动。原子静止时，一个原子平均相互作用能为[15]

(2)

式中的V2为两原子的sp2轨道σ键的共价能，它与原子间距离d的平方成反比

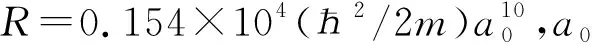
将φ(d)在平衡位置d0附近展开，偏离δ=d-d0很小时，有

(3)

将(2)代入(3)式，求得原子振动的简谐系数ε0、第一和第二非简谐系数ε1、ε2，其表示式见文献[16]。

除石墨烯原子相互作用外，石墨烯电子间也有相互作用，包括：原子间的电子相互作用(称为原子间的关联G)、原子内的电子相互作用(称为内部关联U)。原子静止时外延石墨烯电子系统的哈密顿H为基底电子的哈密顿Hs、石墨烯电子的哈密顿Hg和处于第i个格点的石墨烯与基底的电子之间的相互作用哈密顿Hin之和，即

H=Hs+Hg+Hin

(4)

其中，基底为金属，电子为自由电子，Hs为

(5)

式中的N=NA=NB是基底中电子具有波矢q、自旋为σ=(↑,↓)的态|qσ>的填充数；εs(q)为基底电子波矢q的能量。

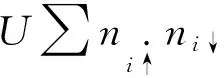
(6)

基底与石墨烯的电子之间相互作用哈密顿Hin为

(7)

将(5)～(7)式代入(4)式，就得到哈特利一福克近似下，不考虑原子振动时金属基外延石墨烯电子系统的哈密顿。

2 电子系统的能量

文献[14]利用格林函数法，求出A、B子格的格林函数，进而求出不考虑原子振动时金属基外延石墨烯电子系统的能量为

(8)

其中，εF为费米能，εdσ为α子格中自旋为σ的一个电子的能量，nασ为α子格自旋为σ的电子数，nA、nB为A、B原子电子数，Es为基底能量。

ρaσ(Ωσ)为a子格中电子自旋为σ，以Ωσ为变量的态密度。

考虑原子作非简谐振动后，石墨烯中要产生大量的声子，电子与声子之间有相互作用，外延石墨烯电子系统的能量E除E0外，还要加上电子与声子之间相互作用能ΔEep，即

E=E0+ΔEep

(9)

电子与声子相互作用能量ΔEep与一个电子与一个声子相互作用能W成正比外，还与产生的声子数nq成正比，即ΔEep∝Wnq。按照统计理论，具有能量为ħωq的声子的数目为

(10)

考虑原子作非简谐振动后，式中的声子频率ωq不是常数，而是与温度有关：

(11)

这里ω(0)是T=0K时石墨烯原子振动的频率，它与原子质量M和简谐系数ε0的关系为：ω(0)=(ε0/M)1/2。还注意到，由于自旋相反的电子与声子的相互作用会抵消，抵消的结果只有[(nA↑-nA↓)-(nB↑-nB↓)]个电子与声子有相互作用。用序参量表示后，系统的电子与声子相互作用能为

(12)

将(12)和(8)式，代入(9)，得到外延石墨烯电子系统的能量为

(13)

3 外延石墨烯的相图

外延石墨烯的磁性和半金属性等主要由电子系统的自旋状态决定，序参量a、b、c、d的情况决定了系统处于何种状态。

3.1 不考虑原子非简谐振动情况

利用(1)式，将nA、nB以及na↑、nb↑等用序参量a、b、c、d表示。近邻格点间电子间的交换作用很小，可设t=0。由(13)式，得到外延类石墨烯的能量E与序参量a、b、c、d和温度T以及U、G等的关系式，即E=E(a,b,c,d,U,G,T)，在a=1，b=0(即一个原胞上有2个电子，磁化强度为零)情况下，外延类石墨烯的BC(c=0、d≠0)态、BZ(c≠0、d=0)态、PM(c=d=0)态电子系统的能量EBC、EBZ、EPM分别为：

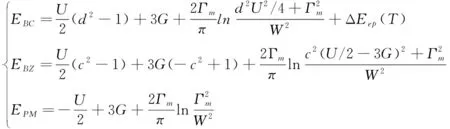
(14)

考虑到原子非简谐振动主要影响的是G，由EBC=EBZ=EPM，得到三相点的关联U、G满足U=πΓm、3G=πΓm+2dΔEep，而序参量满足：

(15)

分别由EBC=EBZ、EBC=EPM和EBZ=EPM得到铁磁-抗磁相变曲线1、铁磁-半金属相变曲线2和抗磁-半金属相变曲线3。

不考虑原子非简谐振动(ΔEep=0)时，由(14)、(15)得到三相点为：U=πΓm、3G=πΓm，序参量c，d满足：

(16)

相变曲线满足：

(17)

3.2 考虑原子非简谐振动情况

(18)

以U为纵坐标，G为横坐标，由(17)、(18)就得到外延类石墨烯的相图。

4 非简谐振动对外延石墨烯相图的影响

现以钨基底上的外延石墨烯为例作讨论。文献[16]已由求得：石墨烯的简谐系数ε0、第一和第二非简谐系数ε1、ε2为：ε0=3.5388×102J·m-2、ε1=-3.49725×1012J·m-3、ε2=3.20140×1022J·m-4。C原子的质量M=1.995017×10-26kg，求得ω(0)=(ε0/M)1/2=1.5296×1014s-1，由(11)式求得ωq(T)，一个电子与一个声子相互作用能W按文献[17]，W=0.5 eV，代入(12)式，求得ΔEep(T)。

将这些数据代入(17)式，得到不考虑原子振动时外延石墨烯的相图如图3。

图3 不考虑原子振动时钨基底外延石墨烯的相图Fig 3 Phase diagram of epitaxial graphene on tungsten substrate without considering atomic vibration

由图3看出：钨基底外延石墨烯中，会出现半金属相、反铁磁相、顺磁相这三种状态，至于出现何种状态，取决于外延石墨烯中原子内部的电子关联U和原子间的电子关联G。只有在原子内部的电子关联U和原子间的电子关联G分别为U=0.33284 eV和G=0.11904 eV时，才会出现半金属相、反铁磁相、顺磁相这三相共存。

将ΔEep(T)和上述这些数据代入(18)式，得到温度T=300 K时，考虑原子振动时外延石墨烯的相图如图4，图中线0、1、2分别为简谐近似、计算到第一非简谐和同时计算到第一、二非简谐项的结果。

图4 考虑原子非简谐振动时外延石墨烯的相图Fig 4 Phase diagram of epitaxial graphene considering atomic anharmonic vibration

由图3和4看出：不考虑原子作非简谐振动时，外延石墨烯的相图与温度无关，即系统的铁磁-抗磁-半金属相变取决于原子内部的电子关联U和原子间的电子关联G，而考虑原子作非简谐振动时，外延石墨烯的铁磁—抗磁—半金属相变还与温度有关：在相同的原子间的电子关联G情况下，考虑原子作非简谐振动后，原子内部的电子关联U要比原子静止时的U增大(即原子内部的电子之间相互作用增强)时，才会发生半金属-反铁磁-顺磁相变。即：考虑原子作非简谐振动后，发生半金属-反铁磁-顺磁相变的条件对原子内部的电子之间相互作用要更强。温度愈高，非简谐效应愈突出，金属基单层外延石墨烯中发生半金属-反铁磁-顺磁相变的条件愈高，发生相变就更不容易。也就是说，低温下该材料中更易发生半金属—反铁磁—顺磁相变。

5 结 论

对金属基单层外延石墨烯的相图的变化规律进行研究，结果表明：(1)考虑到原子的非简谐振动后，金属基外延石墨烯也有自旋态密波(BC)、电荷密度波(BZ)和半金属态(PM)这三种状态，它们的相图和相平衡线不仅与石墨烯电子的直接和间接库仑排斥能U和G有关，而且还与温度等有关，具体关系由(17)和(18)式决定；(2)金属基单层外延石墨烯出现半金属、反铁磁、顺磁这3种相中何种状态，取决于外延石墨烯中的电子关联U和G。只有当U=0.33284 eV和G=0.11904 eV时，才会出现半金属相、反铁磁相、顺磁相这三相共存；(3)原子的非简谐振动对金属外延石墨烯的相图有重要影响：在相同原子间的电子关联G情况下，使发生半金属—反铁磁—顺磁相变对原子内部的电子之间相互作用要更强。不考虑原子作非简谐振动时，外延石墨烯的相变与温度无关。考虑原子的非简谐振动后，外延石墨烯的相变与温度有关，在低温时发生半金属—反铁磁—顺磁相变更容易。