高层隔振结构风致振动的TMD控制

潘骏博， 唐礼平

(1.安徽建筑大学 材料与化学工程学院，安徽 合肥 230601；2.安徽建筑大学 土木工程学院，安徽 合肥 230601)

0 引 言

建筑物的抗震、抗风设计一直是土木工程领域的热点问题,随着社会经济的发展和工程技术的进步,目前高层建筑是我国各城市基础设施建设的重要组成部分,而风荷载往往是高层结构设计的主要因素[1]。

我国建筑抗震设计的研究早于抗风设计,前者技术发展较为成熟,在现行的《建筑抗震设计规范》(GB 50011-2010)中隔振技术已经明确作为规范条文用于指导设置隔震层以隔离水平地震动的房屋隔震设计。设置隔振结构的目的是消耗地震动的能量向上部传输,国内外学者在这方面的研究成果非常广泛,但对于隔振结构的抗风设计研究并不多[2-6]。

TMD用于高层建筑结构地震及风振反应控制取得了丰富的成果[7-10],通常采用在结构顶层布置单/多个TMD的设计方案,目前仍然是学者们的研究热点。

本文采用国际结构振动控制公共平台中的20层钢结构建筑,利用ANSYS软件分别建立其带隔震层以及隔振层和TMD两者相结合的控制结构有限元模型,比较结构在顺风向脉动风荷载作用下的风振反应控制效果。

1 谐波迭加法(WAWS)基本理论

考虑一维,n个变量,零均值的高斯随机过程vj(t)j=(1,2,…,n),其谱密度函数矩阵为:

S(ω)=[s11(ω)s12(ω)…s1n(ω)

s21(ω)s22(ω)…s2n(ω)

…………

sn1(ω)sn2(ω)…snn(ω)]

(1)

式中:sii(ω)为自功率谱密度;sij(ω)(i≠j)为互功率谱密度,可写成复数形式:

sij(ω)=|sij(ω)|eiψ(ω)=sii(ω)sjj(ω)coh(ω)eiψ(ω)

(2)

式中:coh(ω)为相关函数;ψ(ω)为互谱的相位角,采用Davenport脉动风速谱,相关函数可写成:

coh(f)=exp{[-2f(C2x(xi-xj)2+C2z(zi-zj)2)1/2]i+j}

(3)

式中:(xi,zi),(xj,zj)分别为迎风面上的两点坐标。建议空间相关性衰减速度的参数取Cx=16,Cz=10。i为点i的平均风速。

定义ω*=ωΔz2πv(z),Δz为高差,则互功率谱相位角可写成:

ψ(ω)={ωΔz8v(z)ω*≤0.1

-5ωΔzv(z)+1.25 0.1<ω*≤0.125

[-π,π]之间随机数ω*>0.125

(4)

根据Shinozuka理论,随机过程样本可以由下式来模拟:

vj(t)=∑jm=1∑Nl=1|Hjm(ωml)|2Δωcos

[ωmlt-ψjm(ωml)+θml,j=1,2,3…,n

(5)

2 高层隔振结构的TMD控制模型

本文选用的20层钢框架结构模型,结构平面布置图和楼层布置等详见文献[11]。选取整个Benchmark模型的南北方向一榀框架进行分析。有限元建模时将全部地震作用质量分为2部分:钢框架梁柱质量和其他附属物质量。第1层质量508 t,第2层为540 t,3到20层均为526 t,顶层包括防水层以及屋面一共558 t。

结构梁柱模拟:梁柱采用Beam 23单元进行模拟,实常数中截面类型设置采用通用截面。

隔振模拟:本文将隔振层设置在1层柱顶,水平方向选择Combin 40单元,竖直方向选择Combin 14单元。Combin 40单元模拟隔震支座的屈服前刚度Ku、屈服后刚度Kd、屈服力Qd、阻尼比ξ;Combin 14单元模拟隔震支座的竖向刚度和竖向阻尼。根据模型的质量和刚度以及所受风荷载,确定Combin 40和Combin 14单元的实常数。

TMD模拟:设置在结构顶层,TMD阻尼器的质量块和弹簧分别采用Mass 21单元和Combin 14单元来模拟。取TMD的质量为结构总质量的5%、固有角频率ωn=k/m、质量比μ=m/M、阻尼比ζ=c/(2km),其中M为主结构的质量,m、k、c分别为TMD的质量、弹簧刚度和阻尼。隔震结构的TMD控制结构模型如图1所示。

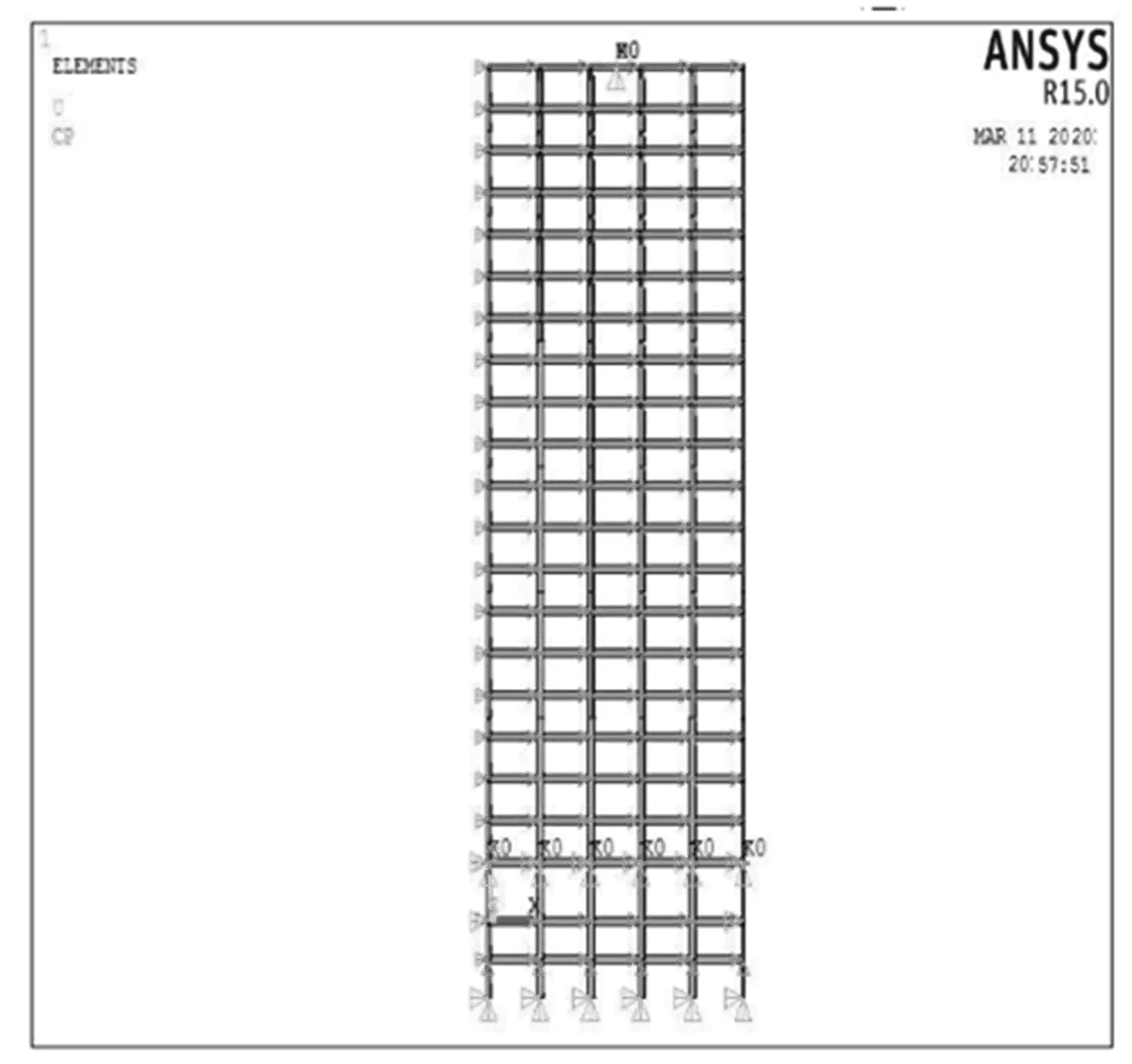
图1 隔震结构的TMD控制模型

3 脉动风场的数值模拟

本文针对20层结构模型,依据Davenport脉动风速功率谱,采用WAWS法模拟生成顺风向的脉动风速时程曲线和风速谱的功率谱密度。

结合工程实际高度和宽度,20个空间点的竖向相关性,模拟时间步长Δt=0.1 s,10=15 m/s,K=0.03,地面粗糙度长度z0=0.4,截止频率ωup=4π,频率等分数N=1 024,cz=10,模拟时程300 s,体型系数μs=0.8。

限于篇幅,本文仅给出了该结构第20层的脉动风速时程曲线以及模拟风速的功率谱密度函数与Davenport目标谱的比较,如图2所示，可以看出在走势上和目标谱比较一致。

图2 结构第20层脉动风速及其功率谱密度曲线

4 风振反应控制效果评价

为了评价本文方法在高层隔振结构风振反应控制上的有效性,表1给出了结构隔振控制、隔振及TMD联合控制下该结构第1、5、10、15和20层的层间位移峰值和水平加速度峰值对比。

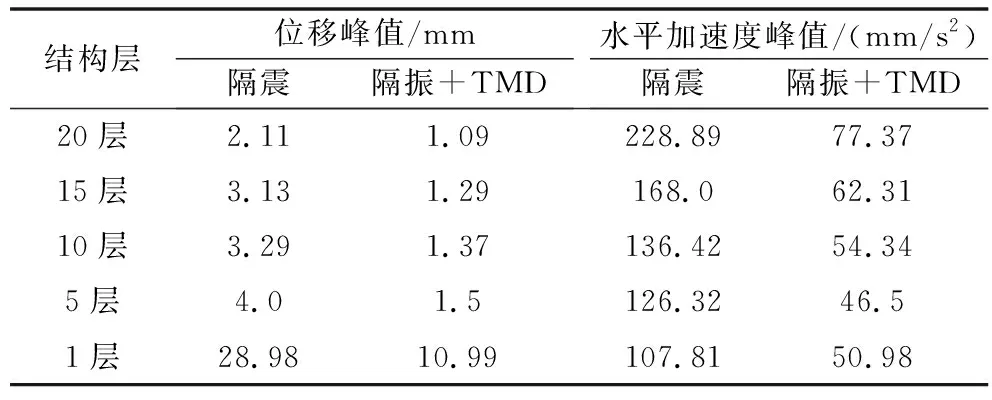
表1 风振作用下结构层间位移及加速度反应峰值

从表1可以看出:

隔振+TMD控制工况多数情况下优于隔震结构。隔震+TMD控制时结构在首层(隔振层位置处)最大层间位移为10.99 mm,而仅设隔震层时首层位移为28.98 mm,隔振层的位移行程显著降低,可以延长隔震层的使用寿命。隔震+TMD控制相比仅设隔震层结构的加速度控制,显示出明显的优越性。

5 结 论

本文从高层隔振结构抗风设计出发,选取20层结构为对象,采用WAWS法对顺风向脉动风荷载进行模拟,利用ANSYS有限元软件对隔振以及隔振和TMD控制结构的风振反应控制效果进行计算比对。结果表明TMD控制可以改善高层隔振结构的抗风性能,提高隔震装置的寿命,可以用于高烈度、高风压地区高层建筑的风振反应控制中。