机械絮凝池内部流场特性的数值模拟研究

舒 在

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

0 引 言

絮凝是水处理工艺中的重要一环,絮凝效果的好坏主要由两个因素决定:一是絮凝剂的性质;其次是水处理构筑物所提供的水力学条件[1]。其中水力学条件对絮体的成长起决定性作用,是决定絮凝效率的关键[2]。因此,对絮凝池进行合理的设计,探讨出最佳絮凝水力学条件显得十分重要。机械絮凝是絮凝的重要组成部分,相比于水力絮凝,对其研究较少,目前对机械絮凝主要通过试验和数值模拟来研究。包雨云等[3]研究不同叶轮直径对方形槽中机械絮凝的影响,结果表明适当对搅拌浆直径进行增大,可提高絮凝效果。NO-sukpark等[4]进行了烧杯模型试验、CFD模拟,以剩余浊度和G值为絮凝效果评价指标,研究方形、圆形、带有挡板的圆形三种不同烧杯装置的絮凝效果,研究结果表明,带有挡板的圆形烧杯装置絮凝效果最好。熊水应等[5]对不同样式搅拌器的机械絮凝池中在水厂中的运行性能进行测试比较,发现水翼式的絮凝效果更优。陈卫等[6]基于CFD模拟水流流态,通过研究两种水力学因素对絮凝效果的影响,即搅拌器的几何尺寸和在容器中的高度,提出了相应的合理工况。鄢碧鹏等[7]基于CFD对不同桨叶速度组合的机械絮凝池内的流场进行了数值模拟,得到了最佳絮凝效果时的速度组合。

这些对机械絮凝反应器的研究都从改变絮凝水力学条件出发,进而强化絮凝工艺过程,且都是对垂直轴式机械絮凝反应器的研究。在实际工程中，机械絮凝池的进水方式、搅拌器旋转方向、各级反应格间过水孔洞形状的改变都会对絮凝水力学条件产生影响,但相关设计规范对这些没有规定,目前都是依据设计者的经验进行设计,难免会产生一定的误差,而这些条件对絮凝效果的影响在现有的研究中还比较少见。采用CFD数值模拟的方法可以对实际尺寸的池体内流动场进行计算,相比试验研究而言具有更快速、更准确、费用更低等优点。因此,笔者选择水平轴式机械池为数值模拟研究对象,研究不同进水方式、搅拌器旋转方向、过水孔洞形状对絮凝水力条件的影响,这对实际工程中絮凝池的设计与运行有一定的指导意义。

1 模型的建立

1.1 几何模型的建立

数值模拟中采用三维实体模型来研究,根据《给水排水设计手册——城镇给水》设计要点及规范要求,单个絮凝池的设计流量为3 000 m3/d,进水直径为800 mm,进口流速为0.69 m/s,絮凝时间为20 min,池体长度14 m,池体宽度83 m,池内设3排搅拌器,每排搅拌器上设3个搅拌器,搅拌器上的叶轮呈十字形安装,叶轮直径为3.3 m,十字叶轮上安装4块桨板,桨板长度为25 m,桨板宽度0.2 m。絮凝池分为3个相同的反应格,第一反应格内搅拌器上桨板中心点的线速度为0.5 m/s,第二反应格内的的桨板中心点线速度为0.35m/s,第三反应格内的桨板中心点线速度为0.2m/s,各排搅拌器之间用隔墙分开以防止水流短路,隔墙上下交错开孔。图1为底部进水的水平轴式机械絮凝池模型。

图1 水平轴式机械絮凝池模型

1.2 数学模型的建立

机械搅拌装置的数值模拟和实验研究表明,对于机械搅拌的三维模拟,采用标准k-ε湍流模型较为合适,其结果与试验数据吻合较好[8,9],因此水平轴式机械絮凝池数值模拟的基本控制方程由k方程、ε方程、连续方程、动量守恒方程组成。

2 边界条件及模拟方法

2.1 网格划分

利用Gambit划分网格,网格单元类型选择Tet/Hybrid的非结构化网格,主要为四面体。对于含有搅拌模型的处理采用多重参考系法(MRF)[10],将单个反应格分为含桨板的旋转区域和桨板以外的静止区域。由于含有搅拌器的旋转区域水流流场变化剧烈,为了保证计算的精度需要对旋转区域的网格进行加密处理,网格节点间距取60。对于静止区域,网格节点间距取80。

2.2 边界条件及求解器

机械絮凝池进口边界条件为速度进口,出口边界条件设为自由出流;近壁区域的处理采用标准壁面函数法[11],搅拌器和搅拌轴的壁面设为移动壁面,其他壁面采用固定壁面边界条件,旋转区域和静止区域的分界面设为interface,自由液面设置为无剪切的对称边界条件。选用标准的k-ε湍流模型,采用SIMPLE算法求解。

3 模拟结果与分析

3.1 絮凝效果评价指标

湍动能k越大,湍动强度越大,水流湍动程度越剧烈,胶体颗粒间接触碰撞概率增大,越有利于絮凝体的形成,絮凝效果也就越佳。湍动能耗散率ε表征流体将湍动能转化为分子热运动动能的速率,ε值越大,流体分子获得的动能越大,絮凝颗粒间碰撞越为频繁,絮凝效果越好,ε是有效能耗,是对颗粒碰撞起作用的那部分能量。涡旋速度梯度G与ε有关,ε越大,G越大,絮凝颗粒有效碰撞频率越高,絮凝效果越好。在传统絮凝池设计中,主要用速度梯度G进行校核,但是近年来许多学者对此提出异议,认为G值仅代表能量的空间平均分布,不能反映各局部能量的分布[12，13],涡旋速度梯度G是速度梯度G的一部分,在紊流情况下,G起主导作用,能反映出絮凝区内部局区域的紊动情况。因此,选用湍动能、湍动能耗散率、涡旋速度梯度为絮凝效果的评价指标。

3.2 模拟方法可行性验证

在实际水处理絮凝过程中G值范围一般为20～70s-1,平均GT值范围为104～105。速度梯度G值和涡旋速度梯度G值计算式如下:

G=102×NμW

(1)

G0=ρεμ

(2)

式中:N为叶轮所耗总功率，kW;μ为水的动力黏度,水温按20 ℃计,μ=102×10-6kg·s/m2;W为絮凝池的有效容积,m3;ρ为水的密度，1 000 kg/m3;ε为湍动能耗散率,m2/s3。

以底部进水、搅拌器顺时针旋转的水平轴式机械絮凝池为例,由桨板尺寸及转速计算得到整个池体的平均速度梯度G为37 s-1,通过数值模拟所得到的池体平均涡旋速度梯度G0为36.53 s-1,两者比较接近。

根据模拟结果,截取Y-Z(X=0 m)截面作为分析截面,其速度云图和迹线图如图2所示。

图2 Y-Z(X=0)处截面速度云图与迹线图

机械絮凝池中的水流湍动主要是靠桨板的旋转驱动水流而形成的,由图2a可以看出第一反应格内水流的流速最高,第三格最小,从桨板外缘到靠近搅拌轴方向速度逐渐减小,且3个反应格中桨板中心线速度与设计的桨板中心线速度基本相符。由图2b可以看出,在桨板作用下,水是顺时针流动的,当撞击到侧壁上时,水流方向发生了变化,模拟所得到的絮凝池内的水流流态与实际是相符的。因此,絮凝池模型是可靠的,数值模拟中参数的设置是可行的。

3.3 不同进水方式及搅拌器旋转方向的模拟

利用机械絮凝池不同的进水方式和搅拌器的旋转方向,可以得到4种不同的模拟方案。不同方案的具体设计见表1所示。

表1不同方案参数设计要求

根据不同方案的模拟结果,可得到不同池体内的湍动能k分布云图,为便于研究整个池体内部流场流态,取叶轮桨板中心点所在的平面为分析截面,不同方案的湍动能分布云图如图3所示。

图3 不同设计方案下湍动能分布云图

由图3可知,机械絮凝池内部湍动能在搅拌器附近比其他区域要高,特别是在桨板最外缘高区域较多,搅拌器所在区域使得整个反应格紊动加剧,并且这种加剧程度随着搅拌器转速的减小而降低。

由不同方案下机械絮凝池各个反应格的体平均湍动能k和体平均湍动能耗散率ε的模拟结果可以看出机械絮凝池内部紊动情况,具体数据见表2～表5。

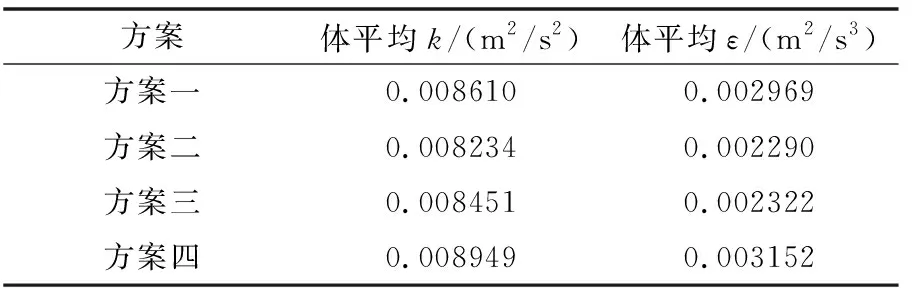
表2 不同方案下第一反应格体平均湍动能k和体平均湍动能耗散率ε

表3 不同方案下第二反应格体平均湍动能k和体平均湍动能耗散率ε

表4 不同方案下第三反应格体平均湍动能k和体平均湍动能耗散率ε

表5 不同方案下机械絮凝池体平均湍动能k和体平均湍动能耗散率ε

由表2～表5可知：

(1)当进水方式同为底部进水,搅拌器顺时针旋转时,水平轴式机械絮凝池各个反应格的体平均湍动能k和湍动能耗散率ε值都比逆时针旋转相对应反应格的值要高,并且这种差异在第一反应格表现明显;当进水方式同为上部进水,搅拌器逆时针旋转的各个反应格体平均湍动能k和湍动能耗散率ε值比顺时针相对应反应格的值要高,同样在第一反应格差异表现明显。这说明了搅拌器旋转方向的改变对絮凝水力学条件的影响较大,且当改变进水方式时,最利于絮凝过程发生的搅拌器旋转方向也发生改变。

(2)当搅拌器旋转方向同为顺时针时,底部进水的机械絮凝池各个反应格都比上部进水的机械絮凝池相对应反应格的湍动能k和湍动能耗散率ε值要高,且差异在第一反应格表现明显;当搅拌器旋转方向同为逆时针时,上部进水的机械絮凝池各个反应格的体平均湍动能k和湍动能耗散率ε值比底部进水的机械絮凝池相对应的反应格的值要高,且差异在第一反应格表现明显。这说明进水方式的改变对絮凝水力学条件的影响较大,搅拌器旋转方向改变时对应絮凝效果最好的进水方式发生改变。

综合四种方案模拟所得的体平均湍动能k和体平均湍动能耗散率ε值进行分析,方案四即采用上部孔洞进水、搅拌器逆时针旋转的水平轴式机械絮凝池第一反应格体平均湍动能k和体平均湍动能耗散率ε值比其他方案要高出许多,在絮凝的初始阶段,絮凝颗粒能发生快速有效的碰撞凝聚成密实的絮凝体,第二、三反应格体平均湍动能k和体平均湍动能耗散率ε值与其他方案相比相差不大,且从整个池体的体平均湍动能k和体平均湍动能耗散率ε值来看,方案四的最高,絮凝效果最好。

由体平均湍动能耗散率ε值计算出涡旋速度梯度G,4种絮凝池设计方案所对应的涡旋速度梯度如图4所示。

图4 不同方案下各反应格涡旋速度梯度

由图4可知,每种方案下,三格反应池的体平均G相差程度逐级下降,这是因为机械絮凝池水流的紊动主要是靠搅拌器的旋转造成,搅拌器转速越大,速度梯度越大,紊动越强,絮凝颗粒碰撞频率越高。方案四中第一反应格体平均涡旋速度梯度达到最大55.86 s-1,第二反应格相对较高,第三反应格与其他方案相差不大,在机械絮凝过程中,第一反应格速度梯度在合理范围内越大,则紊动越强,絮凝颗粒碰撞频率也就越大,更有利于后续反应格絮凝反应的进行,絮凝效果也就越好,从整个池体的体平均涡旋速度梯度来看,4种方案所对应的体平均涡旋速度梯度依次为36.70 s-1、32.82 s-1、32.91 s-1、37.70 s-1,方案四最高。因此,采用上部孔洞进水、搅拌器逆时针旋转形式的水平轴式机械絮凝池絮凝水力学条件最好,絮凝效果最佳。

3.4 不同过水孔洞形状的模拟

基于3.3所得到的结论,对上部孔洞进水、搅拌器逆时针旋转的机械絮凝池反应格之间过水孔洞的形状进行数值模拟研究,3.3中机械絮凝池模型中过水孔洞为长方形孔道,宽为池宽,在控制孔洞面积及孔洞中心位置不变的情况下,对孔洞形状为正方形及圆形的水平轴式机械絮凝池孔进行数值模拟,得出湍动能k和湍动能耗散率ε值,模拟数据见表6、表7。

表6 不同形状孔洞机械絮凝池体平均湍动能k(单位：m2/s2)

表7 不同形状孔洞机械絮凝池体平均湍动能耗散率ε(单位：m2/s3)

在机械絮凝过程中,第一反应格应快速高效地发生碰撞凝结成粗而密实的絮凝体,第一反应格湍动越强,则絮凝效果越好；第二反应格应保持一定的湍动程度使得在第一反应格内没有充分接触的絮凝颗粒再次发生碰撞聚集,同时还可以将未完全压实的大絮凝体打碎,使其重新发生碰撞,以形成致密的絮凝体；在第三反应格内水体应保持较小的湍动强度,防止已形成的絮凝体因湍流剪切过大而破碎形成小体积的矾花,由表6、表7可知,圆形孔洞的机械絮凝池第一、第二反应格体平均湍动能和体平均湍动能耗散率比另两种形状孔洞的要高,三种池体的第三格体平均湍动能和体平均湍动能耗散率相差不大,且从整个池体的体平均湍动能和体平均湍动能耗散率来看,圆形孔洞的最高,由湍动能耗散率算得长方形、圆形、正方形过水孔洞的机械絮凝池涡旋速度梯度分别为37.07 s-1、39.35 s-1、39.15 s-1,可知圆形孔洞的涡旋速度梯度最大。由湍动能、湍动能耗散率、涡旋速度梯度作为絮凝效果评价指标可知对于上部孔洞进水、搅拌器逆时针旋转的水平轴式机械絮凝池,连接各反应格隔墙上的过水孔洞形状为圆形时,絮凝效果最好。

4 结 论

本文研究了不同进水方式及搅拌器旋转方向对水平轴式机械絮凝池絮凝水力学条件的影响,结果表明,进水方式为底部孔洞进水时,对应最佳絮凝水力条件的搅拌器旋转方向为顺时针,反之亦然,即搅拌器旋转方向为顺时针时,采用底部孔洞进水的方式絮凝水力条件最佳;进水方式发生改变时,对应最佳絮凝效果的搅拌器旋转方向发生改变,反之亦然;4种不同进水方式及搅拌器旋转方向的机械絮凝池的模拟结果表明采用上部孔洞进水、搅拌器逆时针旋转的机械絮凝池絮凝效果最好;在进水方式为上部孔洞进水、搅拌器旋转方向为逆时针的基础上,通过对3种不同过水孔洞形状的模拟,结果表明圆形过水孔洞的絮凝水力条件最好。

机械絮凝池中絮凝主要依靠改变搅拌器的旋转方向、提高转速来改善絮凝,因此结构及运行方式的优化设计显得尤为重要。现行的相关设计规范中对水平轴式机械絮凝池的进水方式、搅拌器旋转方向、过水孔洞形状没有规定,主要基于设计者的经验,容易造成设计的随机性,在实际工程中不能提高絮凝效果。本研究为机械絮凝池的优化设计提供了一定的理论依据,对实际工程的应用有一定的指导意义。