基于时间反演法的高强螺栓预紧力监测

王 磊， 任伟新

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

0 引 言

高强螺栓连接由于安装和拆卸方便、整体性好、可靠性高,被广泛运用于大跨度桥梁工程领域和工民建结构当中。相对于普通螺栓而言,高强螺栓的材料强度更高,螺杆可以承受更大的预拉力。因此,在安装高强螺栓时,可以施加更大的扭矩、增加被连接构件之间的摩擦力,从而阻止其产生相对滑移，达到传递外力、减小结构变形的目的。由于高强螺栓在服役期间的安全性的可靠程度关系到整个结构的运行安全,而预紧力不足引起松动是高强螺栓连接节点失效的常见类型[1],因此,对于高强螺栓预紧力的监测具有重要的工程意义。

工程中经常用到的高强螺栓预紧力检测方法有扭矩扳手法、电阻应变片法、结构振动特性法和超声导波法等。扭矩扳手法是通过人工的手段,利用扭矩扳手直接对高强螺栓松动进行检测。由于实际工程中,高强螺栓的数量庞大且部分存在于隐蔽部位,考虑经济成本和作业环境,该方法很难通过人工操作得以实现。电阻应变片法是利用金属丝的电阻值与金属丝的长度、截面积有关的原理,在实际应用中需要与温度补偿片一起使用[2]。电阻应变片法可以在实验室对高强螺栓预紧力检测取得良好效果[3]，应变片与粘贴位置[4]、引线的焊接以及粘贴构件表面的清洁程度有关。基于结构振动特性的检测方法是依据结构动力学参数,包括频率、振型、模态曲率、频响函数、传递函数等，来判断高强螺栓的连接状态。Mewer R等[5]以结构振动响应信号在多个特征频段内的能量分布为特征参数,成功识别出螺栓的松动状态。Cauese V等[6]利用传递函数推导的损伤指标检测出螺栓的松动情况。缑百勇等[7]采用统计学的分析方法,研究了结构的前五阶固有频率来检测螺栓松紧的方法。杨志春等[8]通过分析螺栓松动前后的振动频谱互相关函数幅值向量变化检测螺栓松动损伤。然而,高强螺栓连接状态的改变相对于结构动力学响应的影响不明显,低阶参数对螺栓松动的灵敏度较低[9],实现高频段精确识别结构动力学响应还是存在困难。基于超声波的检测方法作为一种无损检测方法,具有传播距离远、能量衰减弱、灵敏度高等优点[10]。当高强螺栓的受力发生变化时,可以通过声弹性效应检测超声波在螺栓中传播时间的改变,来确定螺栓的轴向力状态[11，12]。通过压电材料激励和接收超声信号的压电主动传感方法,其原理是激励超声波通过螺栓连接界面,分析获得的响应信号能量特征以实现对螺栓连接状态的检测[13，14]。然而在实际工程应用中,直接运用超声波检测的方法会受到环境等因素产生的噪声信号的干扰,噪声信号过高甚至会淹没响应信号,影响对检测结果的判断。

20世纪80年代末,法国科学家最早将时间反演法从光学领域成功运用到声学领域,并给出了时间反演法的定义。由于时间反演法在声学中可以实现信号能量在时间与空间的重新聚焦,因此它可以有效提高信噪比,克服环境噪声的干扰[15]。此后,法国科学家Fink等开始将时间反演法引入Lamb领域,通过试验研究证明了时间反演技术可以有效补偿Lamb波的频散效应。Hoon Sohn等[16]研究发现,利用时间反演法可以有效提高复合材料结构的损伤识别,并通过小波变换改善了Lamb波的时间反演性能。Xu等[17]研究单模式的调整对Lamb波时间反演性能在结构中应用的影响,并在之后提出了一个理论模型分别研究了单模式和双模式的情况下Lamb波的时间反演性能。在国内,王强等[18,19]利用Lamb波时间反演技术以及四点圆弧定位法,研究并提出了基于时间反演技术的损伤的成像法;苗晓婷等[20]则利用Lamb波时间反演技术结合加权分布成像算法实现了对板的多个损伤的识别和定位。在螺栓连接状态监测领域,Wang等[21]利用基于压电有源传感器的时间反演技术对螺栓连接的松紧度进行了研究,结果表明,聚焦信号的峰值会随着螺栓轴向压力的增大而增大,当螺栓的轴向压力达到一定值时,聚焦信号的峰值变化放缓直至饱和。

本文采用压电陶瓷片作为激励器和传感器,利用时间反演技术获得不同预紧力条件下对应的聚焦信号,通过分析聚焦信号峰值随预紧力的变化关系,以实现对高强螺栓预紧力的监测。

1 基于时间反演法的高强螺栓预紧力监测原理

对于高强螺栓连接构件,随着预紧力的增加，螺栓与连接构件贴合得越来越紧密。然而从微观角度分析,高强螺栓与被连构件的表面是粗糙不平的,其实际接触面积要小于名义上的接触面积,超声波在连接界面的传播正是通过实际接触面积进行的。随着预紧力的增加,高强螺栓与连接构件的实际接触面积增加,通过的超声波能量也就越多。

在螺栓连接构件表面布置压电陶瓷(PZT)片,如图1所示。压电陶瓷由于具有正逆压电效应,所以既可以作为激励器也可作为感应器。

图1 试验方案设计

假设PZT1的激励信号(电压)为UA(ω),则PZT2得到的响应信号为:

UB(ω)=UA(ω)Ks(ω)Kp(ω)G(ω)

(1)

式中:Ks(ω)表示PZT2的正压电系数;Kp(ω)表示PZT1的逆压电系数;G(ω)表示结构的传递函数。

由于信号在时域里的反演过程等于其通过傅里叶变换为频域信号的复共轭函数,因此得到时反信号为:

U*B(ω)=U*A(ω)K*s(ω)K*p(ω)G*(ω)

(2)

式中:*表示复共轭运算。此时将时反信号作为激励,从PZT2再次发出,则在PZT1获得的聚焦信号可表示为:

U′A(ω)=U*A(ω)K*sp(ω)Ksp(ω)G*(ω)G(ω)

(3)

其中

Ksp(ω)=Ks(ω)Kp(ω)

K*sp(ω)=K*s(ω)K*p(ω)

由于式(2)中K*sp(ω)Ksp(ω)与G*(ω)G(ω)均为一常数,可以得出聚焦信号与激励信号只存在幅值的不同,因此我们可以通过聚焦信号峰值的大小判断高强螺栓连接状态,实现对高强螺栓预紧力的监测。

2 实验设计与装置

将2块金属钢板采用强度等级为10.9的高强螺栓连接,在螺栓和金属钢板上分别粘贴压电陶瓷PZT1、PZT2、PZT3、PZT4。试样的型号与尺寸大小见表1。

表1 试样规格参数

根据时间反演法的高强螺栓预紧力监测基本原理,设计的试验系统如图2所示。

图2 实验装置

试验通过计算机利用LabVIEW编写的控制程序运行,采用中心频率150 kHz,初始电压为5V的激励信号,如图3a所示。NI-USB-6366数据采集仪将数字信号转换为电压信号,电压信号再经过高压放大器放大,经压电陶瓷的逆压电效应使粘贴在高强螺栓上的PZT1发生机械振动产生超声波。超声波通过钢板与高强螺栓的连接界面抵达钢板上的PZT2,经压电陶瓷的正压电效应转化为电压信号,该电压信号可以被NI-USB-6366数据采集仪采集并储存于计算机中记为响应信号,如图3b所示。将得到的响应信号进行时间反演处理得到时反信号,如图3c所示。将时反信号作为激励信号,再次激励PZT2,此时在PZT1采集到的信号即为聚焦信号,如图3d所示。

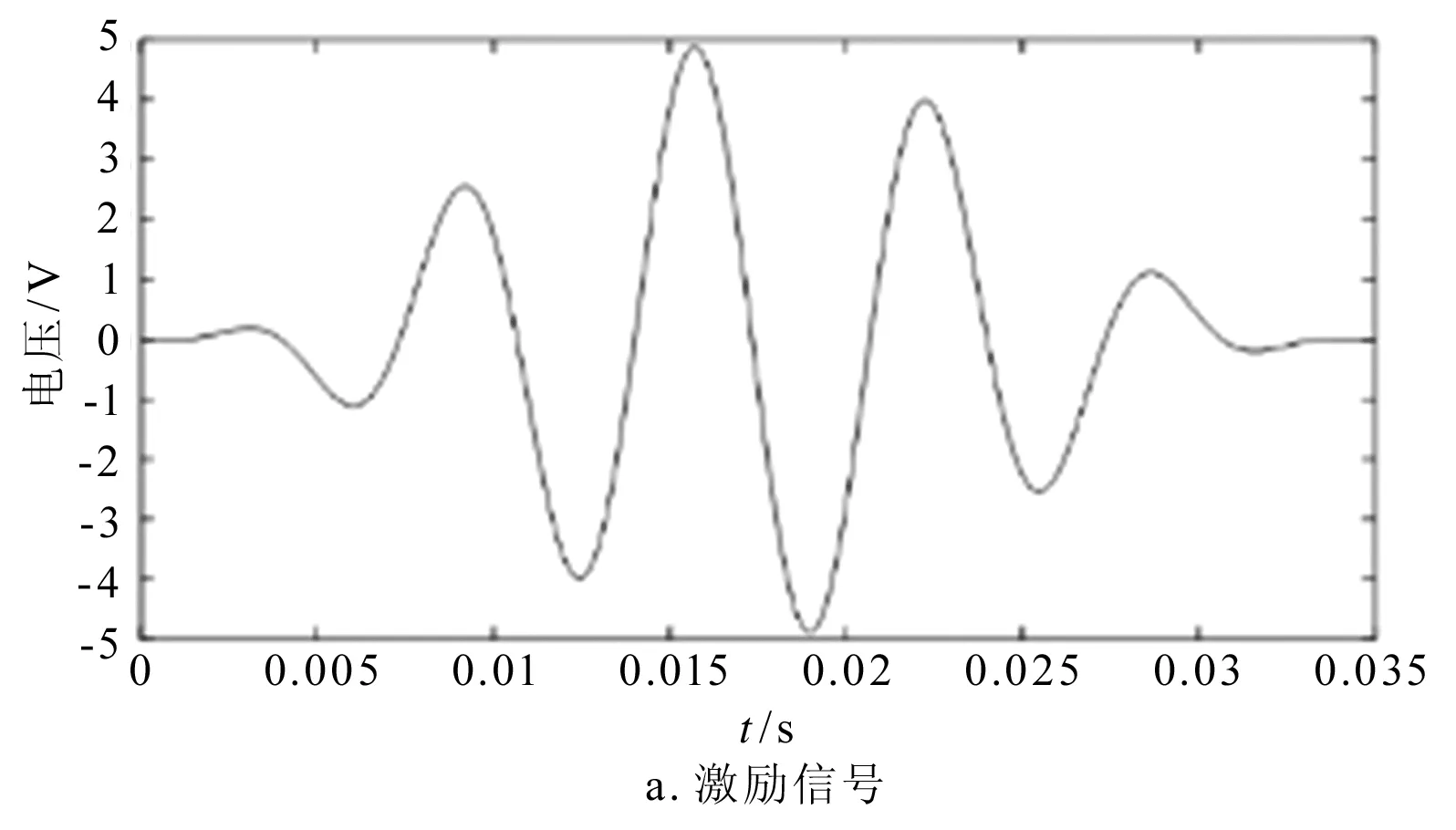
图3 扭矩为6 N·m时的聚焦信号

试验中,高强螺栓预紧力的大小由扭矩扳手控制,扭矩从60 N·m开始,以5 N·m为间距依次减小至0,且每次进行的实验都是将高强螺栓的预紧力从0加载在指定扭矩。为了进一步证明时间反演法对于高强螺栓预紧力监测的有效性,本文还研究了PZT片间距对试验结果的影响。

3 结果分析与讨论

根据上述的试验方案,依次测得在不同预紧力条件下对应的聚焦信号峰值,并建立聚焦信号峰值与高强螺栓预紧力的对应关系,相同的PZT间距,重复测量3次,当PZT间距为5 cm时,所得结果如图4所示。

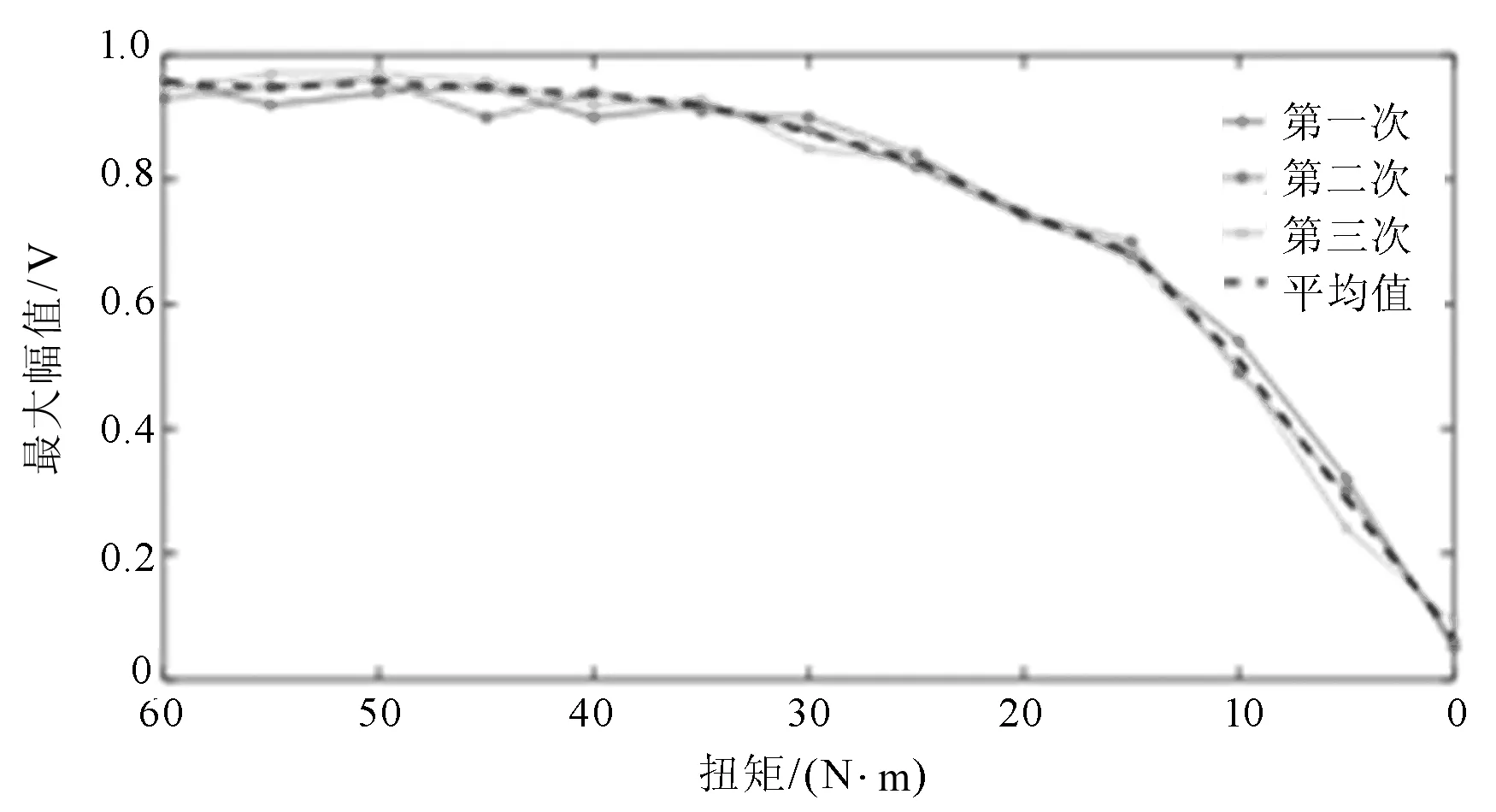
图4 PZT间距为5 cm聚焦信号峰值与扭矩关系

从图4可以看出,当激励器和传感器两个PZT间距为5 cm时,预紧力从60 N·m减至40 N·m之间,聚焦信号的峰值变化不明显,说明在此扭矩范围内高强螺栓处于设计范围的健康状态;预紧力从30 N·m减小至时,此时聚焦信号的峰值变化明显,且随着预紧力的减小而减小。因此可以判断,预紧力小于30 N·m时高强螺栓开始出现松动。当改变PZT的间距后,得到的聚焦信号与扭矩的对应关系如图5和图6所示。

图5 PZT间距为10 cm聚焦信号峰值与扭矩关系

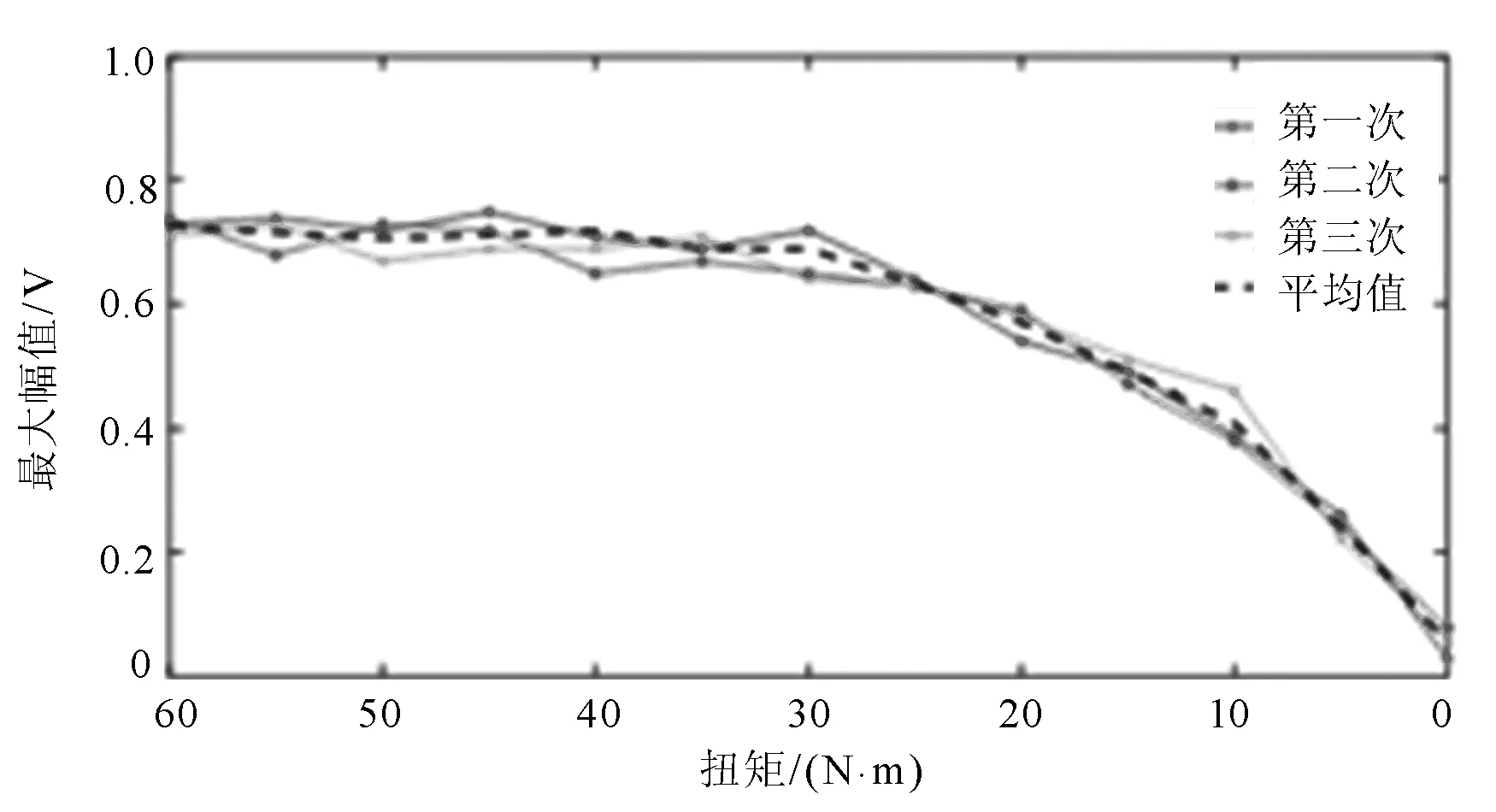
图6 PZT间距为10 cm聚焦信号峰值与扭矩关系

对比图5和6可以看出,当改变激励器与传感器的间距时,由于超声波的传播距离增加,抵达传感器的超声波能量也相应减小,因此聚焦信号的整体峰值降低。然而,随着螺栓预紧力的减少,聚焦信号的峰值的变化趋势与图4保持一致,即聚焦信号峰值变化的拐点依旧发生在30 N·m与40 N·m之间。

对图4、图5和图6试验结果采用计算公式μ=1-(Umax-U)(Umax-Umin)进行归一化处理。所得结果如图7所示,对应指标参数越趋近于1表示螺栓拧得越紧,相反则说明越松动。通过对比可以进一步发现,时间反演技术可以实现对螺栓的连接状态进行有效评估,其结果不受PZT间距的影响。

图7 不同间距的聚焦信号峰值归一化结果

4 结 论

针对桥梁工程中螺栓连接构件的螺栓松动问题,采用时间反演法对螺栓预紧力监测进行了试验研究。试验结果表明:

(1)当螺栓处于拧紧状态时,通过时间反演技术得到的聚焦信号峰值变化不明显;当螺栓处于松动状态时,聚焦信号峰值会小于螺栓处于拧紧状态的聚焦信号峰值,且随着螺栓预紧力的减小变化趋势明显。

(2)虽然改变激励器与传感器的距离会影响整体聚焦信号峰值,但不会影响对螺栓松动的识别,且经归一化处理后,可以实现对螺栓连接状态的有效评估。

(3)通过与响应信号对比,时间反演法具有良好的自适应聚焦特征可以有效提高信号的信噪比,适用于存在噪声环境的实际工程应用。