带循环时间窗口的独立路径配送问题

李 伟，刘 敏，曹庭锴，张同全

(1.云南民族大学 数学与计算机科学学院，云南 昆明 650500； 2.云南民族大学 预科教育学院，云南 昆明 650500)

带时间窗口的物流配送正在当下国家振兴物流产业的背景下高速发展.而该类问题算法的好坏直接或间接地影响到广大人民的经济利益和办事效率，所以对它的研究越来越受到大家的重视也吸引着大批学者对它的关注[1].吴瑶等[2]构建以配送车辆调用成本、行驶成本和产品价值耗损总和最小为目标的优化模型，在货物不可分割配送的前提下，确定车辆离开配送中心的时间和配送路径.梁承姬等[3]提出了带模糊时间窗口冷链物流配送，建立了运输成本、货损成本、时间成本等配送成本最小化和模糊时间窗口进行量化客户满意度最大化的多目标优化模型.王勇等[4]建立了包含生鲜配送车辆的运输成本、温控成本、违反时间窗口的惩罚成本的物流成本模型.李淑琴等[5]建立带软时间窗口约束的多车型车辆路径优化模型，并设计算法，进行了仿真实验.

通过对比发现，前人所讨论的时间窗口无弹性或弹性不够强，一旦关闭就不能再次开放，且没有提及在货物可分割的情况下，受两地之间最大配送量限制的多条独立路径配送.因为本文讨论问题的背景与前人不同，所以时间窗口必然不同.本文通过建立有向赋权网络图上带循环时间窗口的物流配送问题的数学模型，对模型进行预处理，把不定因素转化为固定因素，设计算法，得到带循环时间窗口的独立路径配送问题的一个最优解.

1 问题描述

本文中，物流配送的运费收取方式是以天为单位计算，即配送时间越长，费用越高，配送成本越大.我们考虑的问题为在带循环时间窗口的情况下，选择物流配送路线，使得总运费成本最小.在现实生活中，从任意配送中心i到配送中心j的最大配送量一致，而且不同的两个配送中心i与j之间没有直接到达的配送路线这是可能的，但是我们需要从i配送货物到j，因此我们需要从i出发配送货物到达其他配送中心k，然后再从k出发配送货物到其他配送中心s，如此不断的交替，最后从某一配送中心t出发配送货物到达j.问题是如此交替循环的配送过程中，如何安排货车从不同的配送中心按照不同的时间出发的车辆路线，使得按照该路线配送成本最小.在最大配送量限制下，在一天之内用一条路径完成配送的路线根本不存在是可能的，但是在两天或者多天内用多条独立路径配送是肯定有解的.在本文里，时刻以h为单位，周期以d为单位，一天24h.

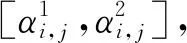
带循环时间窗口的独立路径配送问题的数学描述：图D=(V,A;a,α1,α2,ω,c)，这里a:V→[0,24)为顶点左时间窗口函数，α1:A→[0,24)表示弧的循环时间窗口函数，α2:A→[0,24)表示弧的循环时间窗口函数.权重函数ω:A→R+，表示通过该弧所需要的配送时间，c是定义在弧(i,j)上的容量，且c≡L(L∈N+)其中L为定值，以吨为单位.点s,t∈V，s为源点，t为汇点，令F为从s点出发的总货物质量，F以吨为单位.目标是求满足条件的总配送时间最短的s-t路p1,p2,…,pR，其中R=「F/L⎤.

2 算法设计思路

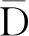
否则，货物不得不等到第2天的发货时间aj才可以继续发货，因此di,j=1，从配送中心i到配送中心j并且货物可以离开配送中心j所需要的为：

即从配送中心出发的时间刚好是检查站的上班时间，那么从点i出发经过弧(i,j)到达点j的时间记为ai+ω(i,j).此时对于任意(i,j)∈D都有(ai+ω(i,j))mod24≤aj+di,j24，其中di,j=0或1.

若(ai+ω(i,j))mod24≤aj，则di,j=0，从配送中心i到配送中心j并且可以从配送中心j准时发货所需要的天数为：

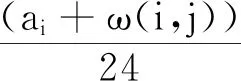
否则，货物不得不等到第2天的发货时间aj才可以继续发货，因此di,j=1，从配送中心i到配送中心j并且货物可以离开配送中心j所需要的天数为：

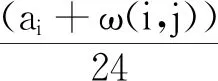
否则，货物不得不等到第2天的发货时间aj才可以继续发货，因此di,j=2，从配送中心i到配送中心j并且货物可以离开配送中心j所需要的天数为：

3 算法设计

算法1预处理算法

输入：带循环时间窗口的独立路径配送问题的一个实例D=(V,A;a,α1,α2,ω,c)，

Begin

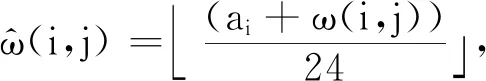
End.

算法2Ford-Fulkerson 算法[7]

输入：独立配送路径问题的一个实例D=(V,A,ω,c)(c=1).

输出：独立配送路径条数K.

Begin

Step 0 取零流为初始可行流

Step 1 求X增广链

1.0给s以标号ls=0，并把所有顶点标为未检查.

1.1如果所有已标号顶点都已检查，转Step3；否则，任取一个已标号未检查顶点i，检查所有于i关联的弧.∀(i,j)∈A，若xij=0且j未标号，则给j标号lj=+i；∀(j,i)∈A，若xji=1且j未标号，则给j标号lj=-i.当所有与i关联的弧都已经检查完毕后，令为i已检查，转1.2.

1.2如果t得到标号，则已找到一条增广链，转Step 2；否则转1.1.

Step 2 对X增广.

2.0 取j=t.

2.2若li=+i，输出(i,j)，令xij:=xij+1，用i替代j，转2.1；若li=-i，输出(j,i)，令xji:=xji-1，用i替代j，转2.1.

Step 3X的流值即为弧独立路径数，输出弧独立路径数K，算法结束.

End.

算法3最小费用路算法[8]

输入：独立配送路径问题的一个实例D=(V,A,ω,c)(c=1).

输出：独立配送路径数值恒和最小的R条路径.

Begin

Step 0 取零流X为初始可行流

Step 1若v(x)=R，结束，X流过的弧构成权值和最小的R条独立路径，否则转Step 2.

Step 2 将X流过的弧全部方向，且令所经过弧权值ω=-ω,得到的网络记为H(x).在H(x)中求最短路P，转Step 3.

Step 3 把X沿P增广1，得到新的X，转Step 1.

End.

算法4带循环时间窗口的独立路径配送问题的一个最优算法

输入：带循环时间窗口的独立路径配送问题的一个实例D=(V,A;a,α1,α2,ω,c).

输出：权值和最小的R条独立配送路径.

Begin

End.

4 算法的可行性分析

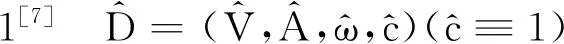
则f+f′是D上流值为v+θ的最小费用流.

定理1算法4是带循环时间窗口的独立路径配送问题的最优算法.

5 算法对比分析

在参考文献[6]中，作者所研究的其中一个问题是图D=(V,A;a,α,ω)，其中a:V→[0,24)为顶点左时间窗口函数，α:A→[0,24)表示弧的左时间窗口函数，权重函数ω:A→R+，表示通过该弧所需要的时间.出发点s∈V和目的点t∈V.求花费时间最少的s-t路.其模型预处理算法为：

当ai≤ai,j

否则，

通过与本文算法1对比可以发现，2个算法都是通过构建有向网络辅助图，把原图中的出发时间和配送(旅行)时间等不确定因素，通过算法转化为有向网络辅助图弧上的天数.这种处理的优点在于通过预处理把不定因素转化为固定因素.但是文献[6]中仅仅只考虑了顶点和弧上同时带左时间窗口的情况，并没有考虑到顶点带左时间窗口，弧上带循环时间窗的情况.本文根据物流配送中实际出现的情况作为考虑因素，建立了以时间成本为目标的数学模型.设计算法，在货物可分割的情况下，得到带循环时间窗下的多条独立路径配送总时间成本最小的一个最优算法.丰富了物流配送路径优化模型，有一定的现实意义及应用价值.本文考虑了最大配送量受限的情况，后续研究中还可以考虑配送中心的储存量受限的情况.