基于改进马尔科夫链的移动轨迹预测方法
王泽天,高 岭,高全力
(西安工程大学 计算机科学学院,陕西 西安 710048)
0 引 言
随着通信技术及移动互联网的成熟与发展,人工智能已经渗透到人们日常生活中的各个角落。特别是近十几年来汽车逐渐走进千家万户,车流量越来越大,交通堵塞和事故频发的问题开始凸显,人们对智能交通的需求也就愈加强烈[1-2]。为了真正实现智能交通,更好地建设及深入研究车联网就变得格外重要。而移动轨迹预测正是车联网技术中的关键环节[3]。移动轨迹预测对于智能交通和人们的日常出行都有着重要作用,精确以及迅速地为驾驶员进行移动轨迹预测,有利于降低道路拥堵,提高出行效率[4-5]。
由于移动轨迹预测与用户本身以及地域之间关系密切,所以在移动轨迹预测方面的研究多是结合城市路网信息和具体位置路况进行分析[6]。LIU等[7]提出了1种循环对数双线性模型,通过模拟历史序列中的短期和长期上下文,实现多种类型的轨迹预测。程媛等[8]提出了基于非参数密度估计的不确定轨迹终点预测方法,通过KS (kolmogorov-smirnov)检验方法与具有相同起点的不确定轨迹模型进行匹配,实现不同条件下的轨迹预测。陈思静等[9]提出了基于马尔科夫链的车辆轨迹预测方法,通过车载自组织网络的特殊应用场景以及车辆移动的规律性,实现对车辆轨迹的预测。乔少杰等[10]提出了基于高斯混合模型的轨迹预测方法,通过高斯非线性概率统计模型,实现准确而高效的轨迹预测。夏卓群等[11]提出1种环境自适应车辆轨迹预测方法,通过历史轨迹数据构造虚拟参考点,利用高斯混合模型训练数据集,实现具有环境自适应性的车辆轨迹预测方法。但是上述方法多是直接采用历史轨迹数据实现预测,对具体路况信息考虑不充分,导致预测精度不高。为此,本文在传统马尔科夫链方法的基础上,通过对车辆轨迹数据的处理并融入具体路况信息,实现对车辆移动轨迹更加精准的预测。
针对马尔科夫链预测算法在预测结果选择时可能出现的偶然性问题,本文提出了改进的马尔科夫链移动轨迹预测(IMCTP)算法。该方法首先采集车辆历史轨迹数据及其发生的场景信息,并生成预测算法所需的数据源;然后利用马尔科夫链算法计算状态转移概率,建立状态转移矩阵,得到移动轨迹;最后将得到的移动轨迹与真实数据进行对比,若存在出入,则将具体的路况信息加入到状态转移矩阵的计算中,进而修正对车辆下一个路口的预测。
1 车辆轨迹数据处理
车辆在实际行驶过程中,其运动轨迹都不一样,必须根据它们各自所特有的运动轨迹来构造状态转移矩阵。首先根据时间顺序将收集到的全部车辆轨迹数据归类,然后再按照车辆的不同运动轨迹对轨迹数据进行划分。也就是,有多少不同的运动轨迹就有多少份轨迹数据[12]。
对于收集到的车辆轨迹数据,先要进行极端或异常数据的删除或者更正。另外,因卫星定位系统偶尔出现的差错,导致它所提供的车辆坐标位置不是车辆的真实坐标。因此,在对车辆轨迹数据预测之前一定要先删除其中不正确的车辆坐标。导致卫星定位系统发生定位错误的因素有很多,例如车辆在偏远山区,信号不能完全覆盖的农村,或者是周围障碍物阻挡了信号的传输等。解决上述问题的方法有:①删除异常轨迹数据。通过设定一个时间标准,如1 min,若发送相邻2次卫星定位的时间差小于1 min,就可以把这条轨迹数据当成异常轨迹数据直接去除。②添加轨迹数据。相反的,若发送相邻2次卫星定位的时间差大于1 min,就依据车辆的平均速度,增添1条轨迹数据。③针对一些特殊情况,如交通事故、临时停车,使得发送相邻2次卫星定位的时间差大于1 min,则先把该轨迹数据进行修正,使其贴近真实轨迹数据,减少后序工作中不必要的麻烦[13-14]。
2 改进的移动轨迹预测算法
2.1 基本概念
1) 路径概率:P1和P2是2个连续的路口,P1、P2之间的n条路径分别用S1,S2,…,Sn表示,L为该路径的长度。所有路口都有几个可行的路口,P1至P2选择St的路径概率见式(1)[15-16]:
(1)
2) 马尔科夫链:马尔科夫链是具有马尔科夫属性的一组离散随机变量。具体地说,对于使用一维可数集作为索引集的概率空间(Ω,F,P)中的一组随机变量X={Xn:n>0},并且该随机变量的条件概率满足以下条件关系[17-18]:
p(Xt+1|Xt,…,X1)=p(Xt+1|Xt)
(2)
则Χ被称为马尔科夫链。
3)k步状态转移矩阵:用户当前所处子网位置以及历史移动轨迹生成的,描述位置状态由一个状态转移到另一个状态的概率,相当于用户由一个位置转移到另一个位置的概率,是马尔科夫链预测的基础。状态转移矩阵P为
(3)
其中:限制条件为
(4)
基于历史移动轨迹,能够得出相邻子网间的转移概率(条件概率),条件概率之上再加条件概率,可得出k步状态转移矩阵[19-20]。
k步状态转移矩阵P(k)可表示为
(5)
2.2 马尔科夫链算法
假设车辆行驶路径中经过路口数为n,那么状态转移矩阵就是n×n的矩阵,其中元素pij所代表的概率是指车辆先行驶到i路口,接着行驶到j路口(j≤n),其表达式为
(6)
式中:Nij代表依次通过相邻的i路口和j路口的轨迹数。在k步状态转移矩阵中每行代表用户当前所在的子网络,每列代表用户在k步后到达的子网络,矩阵中的每个元素表示由当前子网络转移到下一个子网络的概率, 因此, 每行中最大的列即为预测结果。再将预测结果继续代入状态转移矩阵进行迭代, 确定各个位置的预测值,并给出具有最大概率的预期位置, 从而预测出完整的移动轨迹。将用马尔科夫链算法得到的车辆移动轨迹与实际的车辆移动轨迹进行对比,发现预测的结果和真实的结果有明显的误差。 这是由于马尔科夫预测算法每次都会选择最大值, 但当最大值和次大值之间的差过小时,实际行驶过程中选择最大值路口与次大值路口相比是偶然的。所以仅利用马尔科夫链算法对车辆进行轨迹预测不够准确。
2.3 IMCTP算法
IMCTP算法的核心思想是利用已有信息中车辆行驶过次数最多的地点来预测接下来的地点,即
(7)
式中:Pk为车辆选择不同路口的概率。表1为车辆A的状态转移矩阵。通过表1可以看出,假设A当前处在路口3,那么接下来A必然会走路口2。但是在实际行驶中,A通过路口3以后只有1次经过了路口2,这或许是一个偶然情况。假设A当前处在路口2,按照状态转移矩阵,A有5次选择走路口3,4次选择走路口4,这几乎等同于走路口3的频率。因此车辆A走路口3还是走路口4并不确定。
通过优化马尔科夫链算法,给定一个阈值δ(阈值δ介于状态转移矩阵中最大的2个值之间)进行移动轨迹预测。假如最大值与次大值之差大于δ,那么车辆接下来通过的路口等于状态转移矩阵的最大值。当小于δ时,则根据最大值路口是否交通拥堵而采取不同的方法。可以分为最大值路口交通不拥堵、最大值路口交通拥堵2种不同情况。
1) 如果交通不拥堵,则认为车辆通过的下一路口仍然等于状态转移矩阵中的最大值。
2) 如果交通拥堵,则车辆会选择走状态转移矩阵中的次大值路口。
算法的伪代码如下所示:
input:车辆状态转移矩阵M,阈值δ,当前路口i;
output:下一个路口j。
路口A←矩阵中第i行值最大的路口,大小记为v1,路口B←矩阵中第i行值第二大的路口,大小记为v2
if |v1-v2| >δthen
i←路口A
else then
if路口A交通不拥堵 then
j←A
else then
j←B
end if
end if
可以看出IMCTP算法的时间复杂度为O(n2),其中n代表网格中的路口总数。
3 实验与分析
将IMCTP算法与马尔科夫链的轨迹预测算法MC(Markov chain)[21]进行对比。以国内某市交通局发布的8 000多辆计程车在10 d内的8 390条移动轨迹数据为实验数据。随机选择其中6 000条移动轨迹进行预测,其他移动轨迹用来测试预测精度。实验中共有路径138条,87个交叉路口。实验的评价指标为预测精度(A),其计算公式为
A=an/tn
(8)
式中:an为实际行驶轨迹和预测轨迹相同的轨迹数量;tn为全部轨迹预测数量。主要分析预测精度和时间复杂度;车辆连续移动轨迹的预测精度和时间复杂度。
1) 从87个路口中随机选择7个,分别使用IMCTP算法、马尔科夫链算法对轨迹预测精度进行对比,实验结果如图1所示。
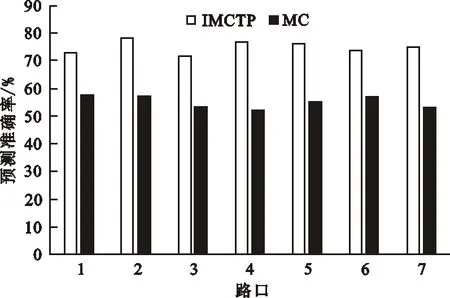
图 1 移动轨迹预测精度
从图1可以看出,IMCTP算法比马尔科夫链算法的轨迹预测精度更高。IMCTP算法的预测精度保持在75%左右,比马尔科夫链算法的预测精度提高了约36%。这主要是因为马尔科夫链算法没有考虑到具体路况信息,导致预测精度偏低。
2) 分别使用IMCTP算法、马尔科夫链算法,对6 000移动轨迹的未来7个路口进行连续轨迹预测,实验结果如图2所示。从图2可以看出,2种预测算法的预测精度会在路口数不断变多的过程中逐渐降低,但IMCTP算法相对保持更高的预测精度。这是因为在迭代计算的过程中,IMCTP算法每次的预测精度都较高。
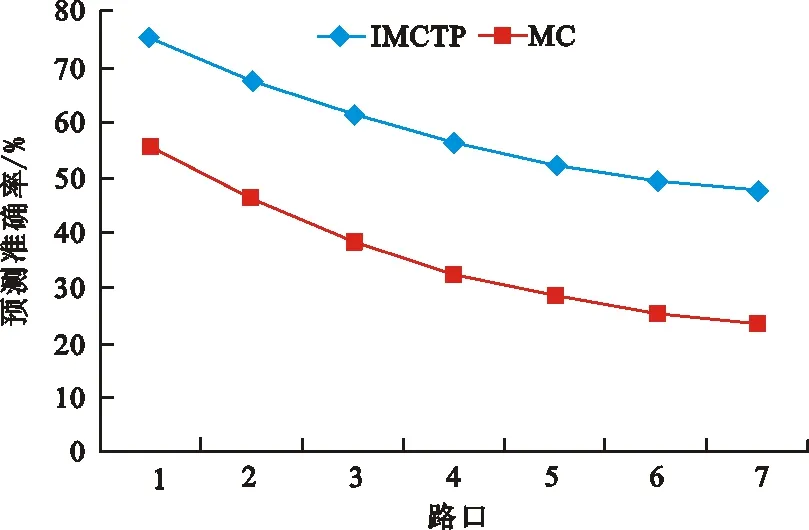
图 2 连续移动轨迹的预测精度
3) 一个优秀的算法不仅应具有较高的预测精度,还应该具有尽可能小的时间复杂度。因此,通过改变轨迹数量来分析2种算法的时间复杂度,结果如图3所示。从图3可知,随着移动轨迹数量的增加,2种算法的预测时间也明显增加,但IMCTP算法的预测时间相对较短。这是因为在车辆移动轨迹数据处理的过程中,删除和修正了一些轨迹数据,从而减少了预测时间。
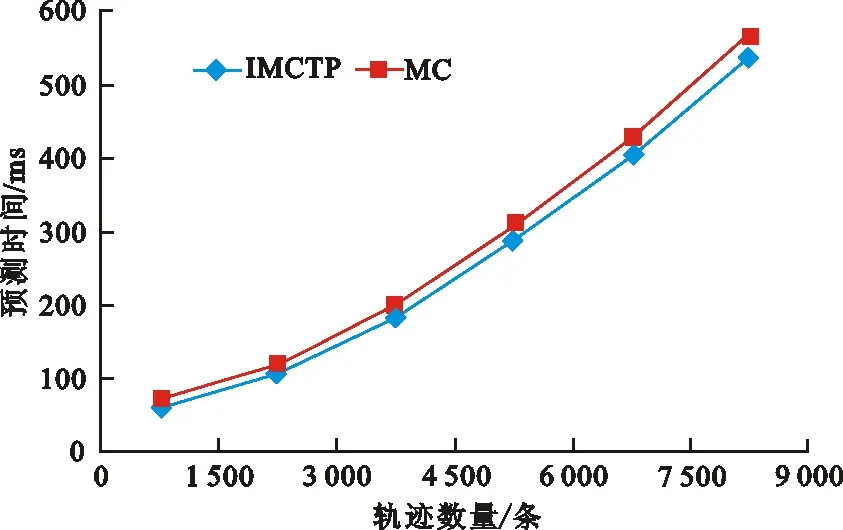
图3 移动轨迹的预测时间
4) 图4为移动轨迹在通过多个路口的预测时间。从图4可知,随着路口数增多,2种算法的预测时间都有所增加,但IMCTP算法比马尔科夫链算法的预测时间较少。这是因为在预测每个路口时,IMCTP算法的预测时间都相对较短,从而迭代计算多个路口时的预测时间也就相应缩短。
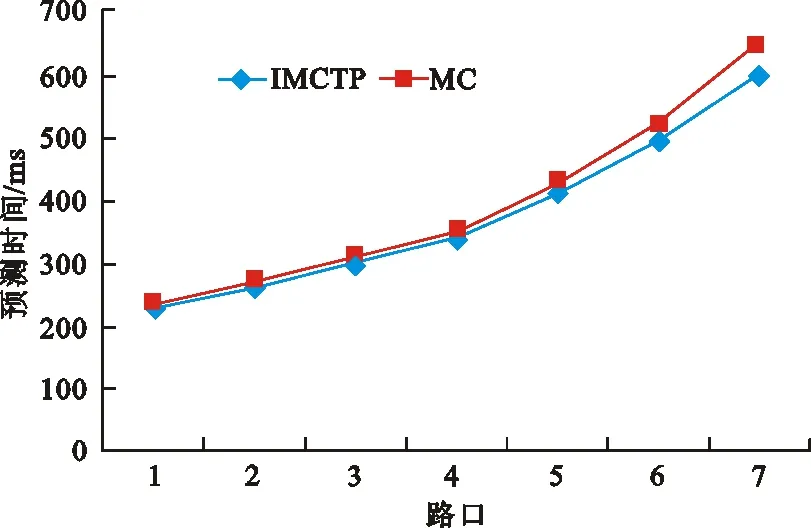
图 4 移动轨迹的连续预测时间
4 结 语
针对马尔科夫链预测算法在预测移动轨迹结果选择时可能出现的偶然性问题,提出了IMCTP算法。该算法首先采集车辆历史轨迹数据及其发生的场景信息,并生成预测算法所需的数据源;然后利用马尔科夫链算法计算状态转移概率,建立状态转移矩阵,得到移动轨迹;最后将得到的移动轨迹与真实数据进行对比。若存在出入,则将具体的路况信息加入到状态转移矩阵的计算中,进而对车辆下一个路口的预测进行修正。
对比实验中,马尔科夫链算法所获得的预测精度远小于理论值,导致这样的预测结果可能是因为具体路况的差异。IMCTP算法的预测精度和时间复杂度比马尔科夫链算法都有明显进步,解决了马尔科夫链算法在预测结果选择时可能出现的偶然性问题,有效融合了车辆行驶过程中的具体路况信息,并可对部分预测结果进行修正,提高了轨迹预测的准确率。

