基于深度学习的多尺度分块压缩感知算法

于 洋，桑国明

(大连海事大学信息科学技术学院，辽宁大连116026)

1 引 言

图像是我们日常生活中一种常见的信息载体，可以很好地帮助我们获取、表达、传递信息.对于自然图像的处理，计算机会将其转化为二维矩阵，以便于处理，在这个过程中必须要满足采样定理，奈奎斯特(Nyquist)定理作为经典的采样定理被人们熟知，由定理可知，要想使采样后的信号尽可能完整地保留原始信号的信息，采样频率至少要大于最高频率的2 倍.压缩感知(Compressed Sensing，CS)［1-3］，用于对信号的压缩采样，也被称为压缩采样或稀疏采样.不同于传统定理，CS 理论对采样频率没有限制，并且可以同时完成对数据的采样和压缩.由CS 理论可知:如果一个信号是可压缩的，或者说，该信号在相应变换域可以被看作是稀疏信号，那么变换后所得的信号通过一个观测矩阵可以被投影到低维空间，且观测矩阵与变换基非相关，要想从得到的少量投影中重构出原始信号，只需要求解一个优化问题即可.

利用CS 理论对二维图像进行处理时，观测矩阵的规模非常大，相应的计算量也会很大.Gan 等人提出了分块压缩感知算法(Block Compressed Sensing，BCS)［4-6］，首先将图像进行均匀分块操作，对图像块使用相同的观测矩阵进行处理，有效地减小了观测矩阵的大小，降低了计算复杂度.但是BCS 算法需要人为选取合适的图像块大小，分块过大就难以达到降低计算复杂度的目的，分块过小又无法保留图像的细节信息.

深度学习［7-9］是机器学习的一个研究方向，在图像处理领域十分受欢迎.深度学习最早被应用于图像识别领域，在1989 年，LeCun 等人利用卷积神经网络对手写数字进行识别，获得了较高的准确率.深度学习方法通过对大量数据进行训练来学习数据中所包含的特征，这种方法也被称为纯数据驱动方法，其放宽了对于输入数据的稀疏性要求，并且可以对训练过程中所需要的网络权重进行自适应地调整，使其更适用于对信号结构的学习［10］.计算机技术不断发展，深度学习方法也不断更新改进，很多领域的学者开始尝试利用深度学习的方法来解决本领域的问题.设计合适的采样矩阵，以及选取最佳的重构算法，是CS 算法的关键步骤，也是算法的核心问题.传统压缩感知理论，测量和重建是分开进行的，并且需要人为地设计合适的观测矩阵，而深度学习方法不仅可以将这一过程变为端到端的框架，突破了传统压缩感知算法对应用深度和广度的限制，还可以利用通用的学习过程从数据中学习所需要的特征，避免了大量的人工特征提取工作，通过组合低层特征形成更加抽象的高层特征.

现有方法多采用全连接层对原始信号进行处理，虽然提高了算法的性能，但是仍然无法有效解决计算量大的问题，对于大尺寸图像的处理仍不能达到理想的效果.为了解决这一问题，本文将深度学习方法与分块压缩感知算法相结合，提出了一种基于深度学习的多尺度分块压缩感知算法(DMBCS)，使用卷积层代替全连接层，减少计算过程中所涉及到的参数量，避免信息冗余，利用多尺度卷积的思想，对原始图像进行多尺度特征提取，在降低计算复杂度的同时保留更多的图像细节信息.

2 分块压缩感知

根据CS 理论:如果一个信号在一个变换域是稀疏的或可压缩的，通过一个观测矩阵可以将信号由高维向低维进行投影，且该观测矩阵与变换矩阵是非相关的，投影后的信号保留了重构所需要的相关信息，因此只需要对一个优化问题进行求解即可完成原始信号的重构［3］.

由CS 算法可知，对于一个长度为N 的实信号x∈RN，可以通过式(1)的线性变换得到x 的n 个线性非自适应观测值.

y∈RM是所得到的采样向量，Φ∈RM×N是观测矩阵，其中M＜＜N.Ψ=［ψ1，ψ2，…，ψN］∈RN×N为一组正交基，若 x 在变换域Ψ 上是稀疏的或可压缩的，即利用很少量的非零值就可以近似求解变换域的信号f=Ψx，并且Ψ 和Φ 是非相关的，就可以通过求解一个非线性优化问题，从n 个观测值中实现对信号x 的重构.

根据BCS 算法，对于大小为Ih×Iw的图像信号，首先将图像分为大小为B×B 的子块，然后对每一个子块采用相同的观测矩阵进行采样，第j 个图像块的观测值如式(2)所示.

xj表示第j 块向量化信号，ΦB为一个 n^×B2大小的正交矩阵即式(1)中的 Φ 如式(3)所示.

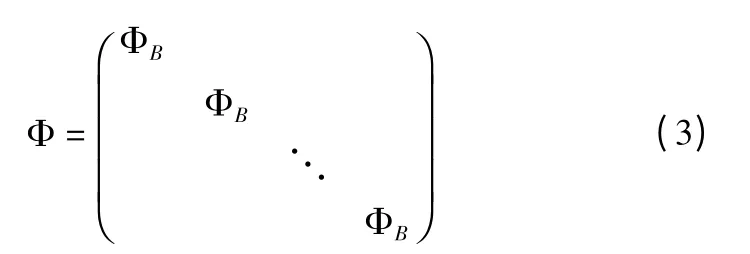
对于信号的重构，BCS 算法采用最小均方误差线性估计对信号进行初始重构:

Φ^B表示重构矩阵，Rxx表示输入信号的一个自相关函数，为观测矩阵ΦB的转置矩阵，式中A－1表示矩阵 A 的逆矩阵.对图像信号进行分块后，观测矩阵ΦB的尺寸很小，可以很容易计算得到Φ^B，有效地降低了存储和计算的成本.

3 基于深度学习的压缩感知算法

利用传统压缩感知算法对信号进行采样，必须满足原始信号在某个变换域下是稀疏的，而使用深度学习方法则没有上述条件的限制，通过提供大量的训练数据，由纯数据驱动算法学习数据的特征结构.

R.G.Baraniuk 团队最先在压缩感知算法中引入深度学习框架［10，11］，从训练数据中学习结构化表示，有效地计算信号估计，并且采用一个无监督的特征学习器，该学习器由去噪自编码器(Stacked Denoising Autoencoder，SDA)堆叠构成，以此来提高信号的重构性能.模型采用线性和非线性两种测量方式.线性测量，首先根据CS 理论的式(1)，采用固定观测矩阵对原始信号进行处理，得到观测信号y，随后采用三层SDA网络，将y 作为输入来重建信号.非线性测量，采用四层SDA网络，第一层进行信号的测量，如(6)所示，后三层与线性测量方式相同，为重建网络，每一层操作如(7)所示.

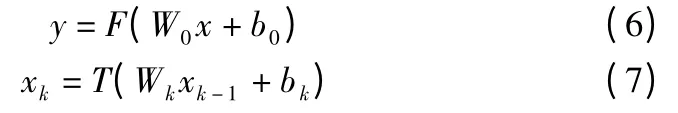
DeepInverse 网络［10，12］学习从观测向量 y 到信号 x 的逆变换，在深度卷积网络(Deep Convolution Networks，DCNs)基础上进行改进，模型包含一个全连接层和三个卷积层.观测矩阵选用固定矩阵Φ，由式(1)可以得到观测向量y∈RM，原始信号x∈RN，将y 作为网络的输入，采用全连接层将输入数据的维数从M 增加到N，全连接层权重值设为ΦT，ΦT表示观测矩阵Φ 的转置矩阵.每个卷积层采用RELU 函数作为激活函数.

ReconNet 网络［13］基于分块压缩感知的思想，把原始图像分为不重叠的子块，将CS 观测值直接映射到图像块，包含一个全连接层和六个卷积层.根据式(1)，y 是M 维的向量表示观测值，x 表示图像块.采用全连接层对输入进行压缩观测，除了最后一个卷积层，其他层在卷积之后使用RELU 函数作为激活函数.每一层产生的特征图大小与图像块大小相等.

CSNet［14］基于分块压缩感知的思想，采用卷积层代替全连接层进行采样，采用单一尺寸，分块尺寸人为设定.对于初始重构的结果，采用三个卷积层进行进一步优化，每一个卷积层包含卷积和池化两个操作.

4 基于深度学习的多尺度压缩感知算法

本文模型包括采样层、重构层、卷积自编码器.

根据BCS 算法，首先将输入的原始图像分为大小相同的不重叠的图像块，与上述深度学习框架下的压缩感知算法不同，本文将不使用全连接层，而是采用卷积层进行代替，并且在卷积层采用了多个尺度的卷积核对上一层的特征图进行处理，与传统卷积操作不同的是，本文采用的是深度级可分离卷积操作.

4.1 卷积神经网络(Convolutional Netural Network，CNN )

CNN 网络［15-17］是深度学习方法中的一种判别架构模型，被广泛应用于图像处理.传统的人工神经网络，采用全连接的方式构建网络，对于自然图像信号来说，距离相近的像素点关联性较强，距离较远的像素点关联性较弱，若采用全局感知的方式必然会造成参数数量的增加.卷积神经网络具有局部感知和权值共享的特性，可以有效解决参数冗余的问题，局部连接指卷积层特征图的每一个单元通过卷积核与上一层特征图的部分单元相连接.权值共享是指一个特征图中的全部单元共享相同的卷积核.

传统的卷积神经网络由卷积层、池化层、全连接层堆叠而成.卷积层的作用是完成对信号特征的提取，池化层可以对输入的特征图进行压缩，完成特征筛选和降维，全连接层是将所提取的特征进行整合.常见的模型包括 LeNet-5、AlexNet、GoogLeNet、VGGNet、ResNet 等.其中 LeNet-5 是最早的 CNN模型，而AlexNet［18］更被人们熟知，其定义的前馈卷积神经网络，成为了深度学习在图像处理领域所使用的主体框架.VGGNet［19］在 AlexNet 的基础上，采用了更多小尺度卷积核，以串联堆叠的方式代替原有的大尺度卷积核，使得网络能提取到更丰富的特征.GoogLeNet［20］利用稀疏连接代替全连接以减少参数数量.ResNet［21］只需要学习信号之间的残差关系，降低了网络学习的难度.

4.2 深度级可分离卷积

深度可分离卷积(Depthwise Separable Convolution)［22，23］可以分解为两步，深度卷积(Depthwise convolution)和逐点卷积(Pointwise convolution).与标准的卷积操作不同，Depthwise convolution 可以针对每个输入通道采用不同的卷积核，即一个卷积核仅对一个通道进行卷积，如图1 所示.Pointwise convolution 采用 1×1 卷积核对 Depthwise convolution 的结果进行结合，如图2 所示，其中卷积核大小为D×D×M，M 为输入的通道数，N 为输出的通道数.比起标准的卷积操作，Depthwise 卷积操作减少了参数量，并且对每个通道都进行了学习，得到的特征质量更佳.

图1 深度卷积过程Fig.1 Depthwise convolution

图2 逐点卷积过程Fig.2 Pointwise convolution

4.3 多尺度卷积

传统卷积网络每一层使用一个尺寸的卷积核，而GoogLeNet 和Inception 网络［24］对同一层的特征图使用了多个不同尺寸的卷积核，以获得不同尺寸的特征，再把这些特征结合起来，如图3 所示.

基于多尺度卷积的思想，本文采用多尺度卷积核对原始图像信号进行卷积操作，以实现图像的多尺度分块采样.每一次卷积可以得到一个特征图，将多尺度卷积所得到的多个特征图进行拼接融合，使得最终的特征图包含的信息更加全面多样，更有利于复杂特征地提取.

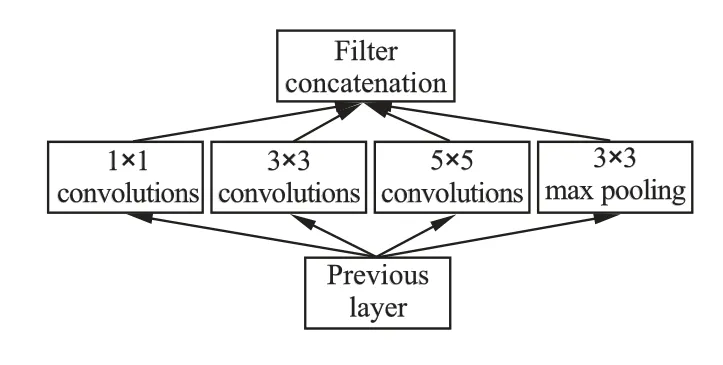
图3 Inception 网络Fig.3 Inception net

4.4 卷积自编码器(Convolution Auto-Encode，CAE)

自编码器［25，26］是一种数据的压缩算法，其中数据的压缩和解压缩是数据相关的、有损的、从样本中自动学习的.自编码器包括输入层、隐藏层和输出层.

自编码器包括编码和解码两个过程.编码过程是为了对数据进行压缩，通过一个非线性函数完成数据从输入层到隐藏层的映射，具体过程如(8)所示.

h 表示经过激活函数后映射到隐藏层的神经单元，f 表示编码函数，W1表示连接输入层和隐藏层之间的编码权重矩阵，b1为偏置，S1表示编码器激活函数.

解码过程就是利用编码所得的隐藏层重构出原始输入数据，如式(9)所示，g 为解码函数，W2表示连接隐藏层和输出层之间的解码权重矩阵，b2为偏置，S2表示解码器激活函数.

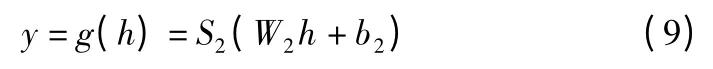
与传统自编码器不同，卷积自编码利用卷积操作代替了矩阵内积操作，更适合图像信号这类二维数据的处理.

4.5 基于深度学习的多尺度分块压缩感知算法

4.5.1 采样层(Sampling Layer)

基于多尺度卷积的思想，采样层使用三种不同大小的卷积核，得到三个特征图，再将其进行融合，得到最终的特征图.采样层首先将原始图像分为大小为B×B 的图像块，b 表示通道数，则每一个卷积核的大小为B×B×b，卷积操作步长为B×B.采样过程如式(10)和式(11)所示，Wdepth表示n个B×B×b大小的卷积核，n=? pbB2」，p 表示采样率.* 表示卷积操作，x 表示原始图像.Wpoint中卷积核大小为1×1×n.采样算法如算法1 所示.

4.5.2 重构层(Reconstruction Layer)

在重构层，首先对采样层的结果进行reshape 操作，再对上述结果进行concatenate 操作，将图像块按行进行拼接，然后通过stack 拼接操作，调整矩阵形状，将图像块重构为完整图像.过程如式(12)所示，其中 γ(.)表示 reshape 函数，ω(.)表示concatenate 函数.

根据多尺度卷积过程，将三个特征图的最后一维进行并联，将并联结果进行卷积操作，得到最终的特征图，过程如图4 所示.卷积核大小为 1×1，步长 strides 为 1×1，填充方式padding 为不填充.

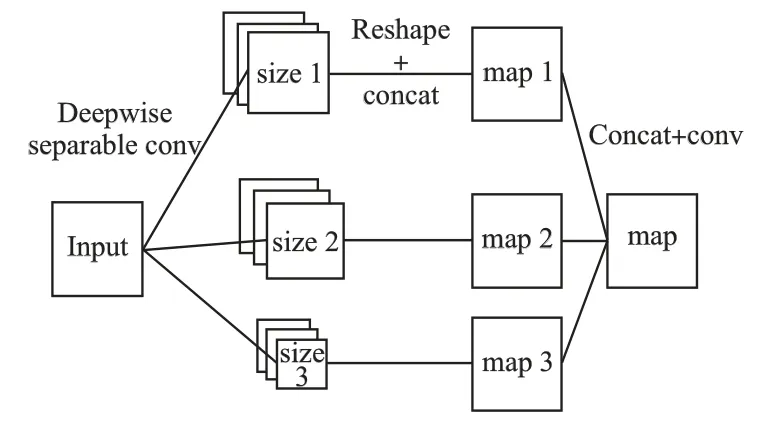
图4 特征图提取过程Fig.4 Feature extraction processing

4.5.3 卷积自编码

本文卷积自编码器分为编码(encode)和解编码(decode)两个部分，并且采用卷积层代替全连接层.本文填充方式选择全0 填充，可以使卷积后的图像大小与原始图像大小相同，同时可以防止图像边缘信息丢失，需要填充的像素点个数如式(13)所示.

其中n 表示卷积核大小，N 表示要处理的图像大小，当n－1为偶数，即n 为奇数时，补充的像素点可以对称分布.奇数维度的卷积核具有中心点，更有利于确定位置.

卷积核大小代表了感受野的大小，大尺寸的卷积核虽然可以获得更多的特征信息，但计算过程中涉及到的参数数量更多，经典的VGG 模型就采用小尺寸卷积核堆叠来代替大尺寸卷积核，有效地提高了计算性能.因此本文在卷积层使用3×3 大小的卷积核，步长设为1×1，使输出矩阵的大小与输入矩阵大小一致，再利用池化层进行降维操作.

池化后输出矩阵大小计算如式(14)所示，利用池化层实现降维效果，步长选择2×2，使输出矩阵大小降为原始大小的一半，为了保证池化过程中不产生重叠区域，池化窗口大小与步长相同，在降维的同时保证不丢失图像特征.

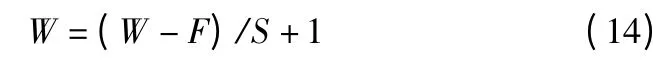
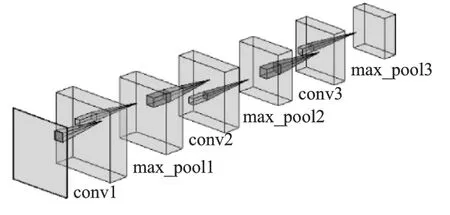
图5 编码过程Fig.5 Encoding processing

编码部分采用三层卷积层加池化层.编码过程如图5 所示，具体参数为:

第一层卷积(conv1)，卷积核大小为 3×3×64，步长strides 为 1×1，填充方式 padding 为全 0 填充，激活函数选择RELU 函数.

第一层池化(max_pool1)，池化窗口大小为2×2，步长strides 为 2×2，填充方式 padding 为全 0 填充.

第二层卷积(conv2)，卷积核大小为 3×3×32，步长strides 为 1×1，填充方式 padding 为全 0 填充，激活函数选择RELU 函数.

第二层池化(max_pool2)，池化窗口大小为2×2，步长strides 为 2×2，填充方式 padding 为全 0 填充.

第三层卷积(conv3)，卷积核大小为 3×3×16，步长strides 为 1×1，填充方式 padding 为全 0 填充，激活函数选择RELU 函数.

第三层池化(max_pool3)，池化窗口大小为2×2，步长strides 为 2×2，填充方式 padding 为全 0 填充.

解码部分采用上采样层加反卷积层，如图6 所示，上采样层选择最近邻插值法.

图6 解码过程Fig.6 Decoding processing

第一层卷积(conv1)，卷积核大小为 3×3×16，步长strides 为 1×1，填充方式 padding 为全 0 填充，激活函数选择RELU 函数.

第二层卷积(conv2)，卷积核大小为 3×3×32，步长strides 为 1×1，填充方式 padding 为全 0 填充，激活函数选择RELU 函数.

第三层卷积(conv3)，卷积核大小为 3×3×64，步长strides 为 1×1，填充方式 padding 为全 0 填充，激活函数选择RELU 函数.

第 4 层卷积(conv4)，卷积核大小为 3×3×1，步长 strides为1×1，填充方式padding 为全0 填充，激活函数选择Sigmod函数.

5 数据集及实验结果

本文采用COIL-100 作为实验数据集，对比算法采用上文提到的 SDANet，DeepInverseNet，ReconNet，CSNet.

5.1 数据集

COIL-100 是由哥伦比亚大学图像库发布的数据集，该数据集是由100 个不同物体在360 度旋转中以每个角度成像所组成，每隔5 度拍摄一幅图像，每个物体拍摄72 张图像，每张图像大小为128×128.本文对数据集中的每一张图片进行平移、旋转、镜像操作对数据集进行了扩充，得到30000 张左右图像.

5.2 实验结果与分析

实验环境采用 windows7 系统，python 编程语言，以及Tensorflow 框架.

本文采用不加噪图像进行训练，采样率分别采用0.5、0.3、0.1、0.05，每个小批次包含 128 个训练图像，共计迭代1000 次，学习速设定为固定值0.0001，损失函数采用均方误差(Mean-Square Error，MSE)，计算过程如式(15)所示.

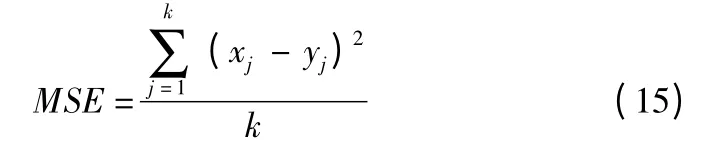
图7 表示当采样率为0.1 时，各个算法的模型训练过程.从图中可以看出，本文算法更优于其他方法，随着迭代次数的增加，损失函数值逐渐趋于0.0001，它反映了模型对数据的拟合程度，即预测值和真实值之间的差距，损失值越小，拟合度越好，模型鲁棒性越好.

图7 模型训练过程对比Fig.7 Model training process comparison

本文采用加噪图像进行测试，采用峰值信噪比(Peak signal-to-noise ratio，PSNR)作为比较参数，计算过程如式(16)所示，图8 表示在不同采样率下，各个算法计算所得的PSNR 值.

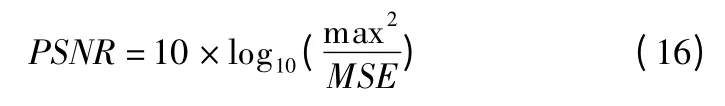
PSNR 是图像压缩重构算法的常用评估指标，其中max表示信号中的最大像素值.PSNR 值越大，说明图像失真越小，图像质量越好.根据图8 及表1 中的具体数据，可以看出，本文算法所得PSNR 值接近40dB，相较于其他算法，对图像重构的质量更有保证，性能更优.

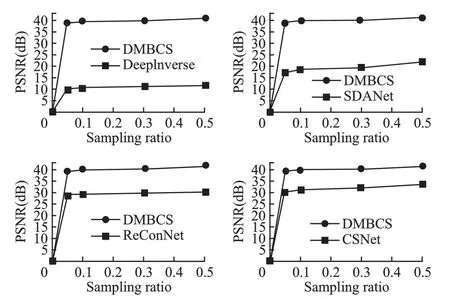
图8 不同采样率下PSNR 值对比Fig.8 PSNR comparisons with different sampling ratio

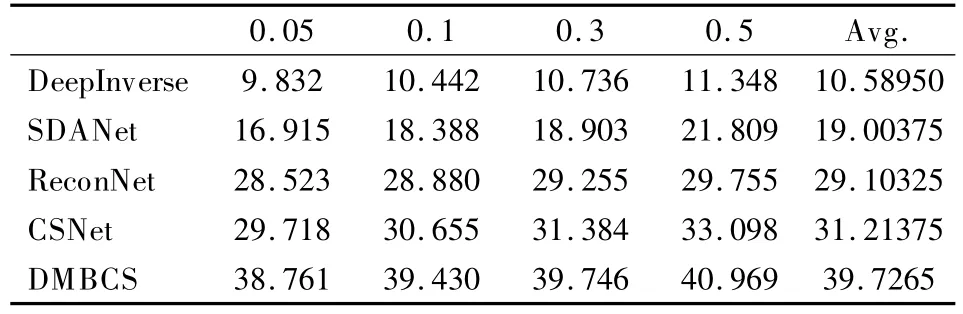
表1 不同采样率下PSNR 值对比Table 1 PSNR comparisons with different samplingratio

6 结 论

本文提出了DMBCS 算法，利用深度学习的方法实现对图像的多尺度分块压缩重构，避免了大量的人工特征提取工作.采用多尺度分块，有效解决了分块大小影响图像重构质量的问题，在减小观测矩阵大小的同时可以保留更多的细节信息.采用卷积层代替全连接层，减少了参数数量，降低了计算复杂度.与其他深度学习框架下的压缩感知算法的对比结果表明:本文算法性能更优，算法鲁棒性更好，图像重构质量更好.

根据BCS 算法，所有图像块都是不重叠的，为了尽可能减小由于分块产生的块效应，进一步提高重构图像的质量，下一步将考虑对原始信号进行重叠分块，并根据图像块的纹理复杂程度采取不同采样率进行处理.