深度信念网络在云安全态势预测中的应用

赵国生，晁绵星，谢宝文，王 健

1(哈尔滨师范大学计算机科学与信息工程学院，哈尔滨150025)

2(哈尔滨理工大学计算机科学与技术学院，哈尔滨150001)

1 引 言

随着云计算成为各领域应用的IaaS，近年来与大数据、物联网和区块链等新兴技术的不断融合发展，云的安全问题越来越突出.云安全态势是根据云计算设备的实时运行状况、服务模式、服务内容以及租户行为等安全需求因素所构成的整个云环境当前的安全状态和变化趋势.态势预测是在云计算环境下做实时安全性分析，对能够引起云安全态势发生变化的要素进行捕捉［1］.研究人员最初从安全威胁［2，3］，脆弱性［4，5］等单个要素上的预测开展研究，后来研究人员开始意识到需要从整体出发考虑安全态势.刘玉玲等从虚拟机安全、用户行为安全等方面构建云环境安全态势感知模型［6］，并引入灰色理论和不确定性模型来实现云环境安全态势要素间模糊影响关系测度，但是在对云环境中安全态势要素信息提取时，账户策略指标不能全面反映安全趋势导致态势预测限于局部性.Chatterjee 等［7］研究了在云环境下如何利用海量安全数据，基于非线性自回归方法的软件故障预测，并通过深度学习进行特征提取和模型训练来提高安全态势的效率和准确性，但并未研究攻击事件实时的预测技术.冯登国［8］等提出了基于时空维度分析的脆弱性预测算法，该算法能够预测未来不同时间段内的脆弱性集，因脆弱性的出现是一个比较随机的事件，仅从脆弱性无法全面预测态势演化过程.云安全的实时运行状况信息和态势演化之间存在着必然联系，这种联系可以通过对云环境下态势要素的态势数据进行深度学习模型的训练和挖掘，可有效解决云安全态势的预测问题.

本文首先对云安全环境建立综合态势指标体系，包括云安全态势一级数据指标和二级数据指标，然后应用深度信念网络(Deep belief network，DBN)来预测云安全态势.同时，对结合改进差分进化算法的深度信念网络(Deep belief network based on improved differential evolution，IDE-DBN)的隐含层参数进行优化，通过引入二维旋转交叉(Two dimensional rotation crossing，TRC)策略和自适应机制，用来扩大种群进化多样性和增强网络的自我调优能力，以提高模型预测的准确度.

2 云安全态势要素指标体系

云安全所涉及的评估指标目前行业还没有统一标准，云安全态势数据的多源、异构、数据量大等复杂性导致性能评估指标纷繁复杂，指标选取的多与少都各有利弊.结合现有文献的相关研究成果，本文根据服务模式、服务内容，租户对云计算系统具有相应的安全性需求对云安全环境引入模型分析，建立可度量的指标体系，该体系的定量描述需要根据云环境实时和历史的运行状态［9］.从云安全性可量化分析的角度提出云环境的脆弱性分析、生存性、威胁性分析以及平稳性分析［10］，分别对应 T1、T2、T3和 T4四个一级指标，这四个层次可以涵盖云环境中大部分的数据实体［11］，然后对上述四个一级指标定义细分的二级指标［12］，得到云环境中各种实体的态势要素数据评估源.比如云端异常数据的捕获、流量数据的还原与监控、扫描类的数据、各类日志数据等.把来自不同的源头、不同类型的异构数据融合、关联在一起，进而通过数据分析发现问题.云安全态势要素指标体系如图1 所示.

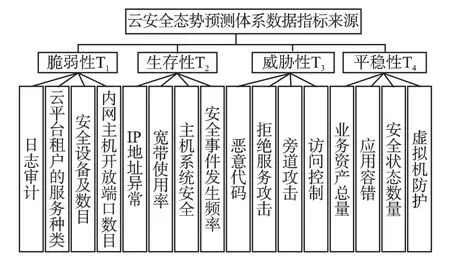
图1 态势要素的指标体系Fig.1 Index system of situation elements

根据国家应急预案的安全需求，并结合图1 中的四类态势要素指标，可以把云安全的态势等级按照［0，1］区间的态势指数定量划分为五个等级.然后把影响预测的态势要素集表示为R=［t1，t2，……，ti］，I 为安全，II 为轻度危险，III 为比较危险，IV 为中度危险，V 为高度危险，输出态势等级如表1 所示.

表1 云安全态势等级表Table 1 Level of cloud security situation

态势要素指标数据源的处理过程:首先，云安全态势数据的收集阶段，包括数据获取对象、范围、数据的处理等.通过融合算法对评价指标集进行数据集合划分得到训练集、测试集和验证集三类云安全态势样本集［13］.然后，结合时间序列滑动窗口实时态势的更新，利用IDE-DBN 神经网络模型对样本训练，得到训练的模型参数;最后依据模型预测输出的云安全态势等级，判断云环境的整体安全性，数据处理过程如图2 所示.

3 深度信念网络

DBN 是一种具有多隐含层的神经网络分类、识别和预测模型，相对于浅层机器学习和传统的神经网络，包含大量隐含层的DBN 对云计算环境异常数据流有良好的特征提取和识别能力.通过多层的非线性变换，从复杂的云安全态势数据中训练出深层次的抽象特征，描述数据的内在关联，采用逐层训练的方式，克服了前馈神经网络易陷入局部极小值的缺陷，获得更优的预测结果和更快的收敛速度.

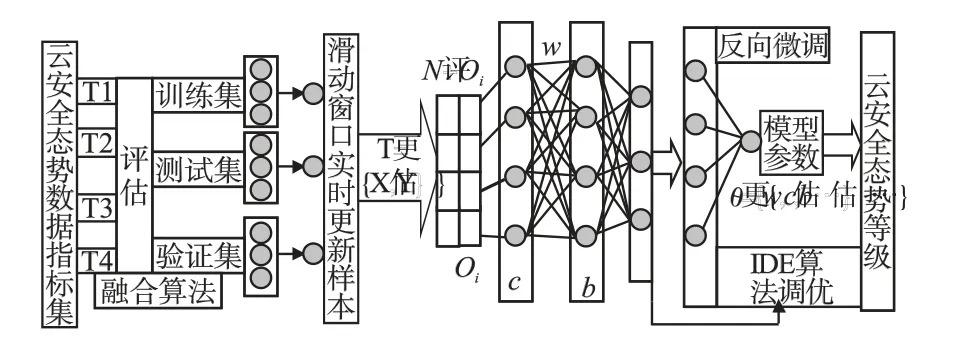
图2 数据处理过程Fig.2 Data processing

3.1 样本输入

采用支持向量分类机(Support vector classification，SVC)模型对采集到的四类历史样本数据集，依据现有文献的评估方法得到当下云安全态势评估等级集合Q={qi}，qi为云网络在i 时刻的态势评估等级值，然后评估集合Q 转换成DBN网络的输入数据集T，如公式(1)所示.

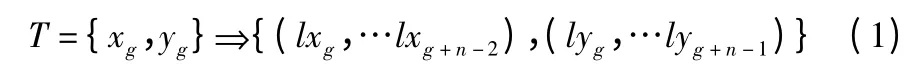
其中，xg为输入特征矢量，yg为标签值，g 为滑动窗口序号，n为滑动窗口大小，窗口滑动步长1，n≤N，g≤N－n.

3.2 训练阶段

DBN 采用无监督的预训练和有监督的全局微调两个步骤实现对神经网络权重的调整.预训练中每个受限玻尔兹曼机(Restricted boltzmann machine，RBM)单独训练，低层到高层逐层训练.微调阶段是利用后向传播算法BP 神经网络来微调DBN 的权重和偏置，DBN 结构如图3 所示.

图3 DBN 的结构Fig.3 Structure of DBN

RBM 通过非监督逐层贪婪的方式预训练获得生成模型的权值，神经网络训练时将可视值映射给隐含层节点，隐含层节点重建为可视节点.每个节点取值都在集合{0，1}，即存在任意的 i，j 使得 vi∈{0，1}，hj∈{0，1}，wi，j为可视层节点与隐含层节点之间的权重，可视节点偏移量c=(c1，c2，…，ci)，隐含层节点的偏移量 b=(b1，b2，…，bj).对于有 i 个可视节点和j 个隐含层节点的RBM，h 和v 分别表示隐含层节点和可见节点的状态，设一组给定的状态(h，v)，RBM 能量函数定义如公式(2)所示［14］.

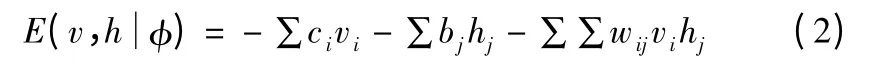
其中，φ=(ci，bj，wij)表示 RBM 参数由公式(2)得到(h，v)的联合分布律如公式(3)所示.

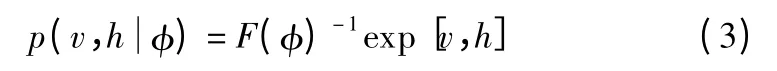
其中，E 为期望值，F(φ)为归一化因子，如公式(4)所示.

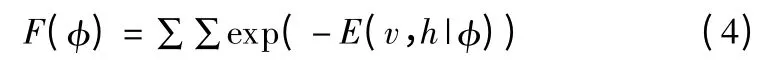
已知可见层的情况下，所有隐含层节点之间相互独立，隐含层中第j 个节点的概率分布如公式(5)所示.

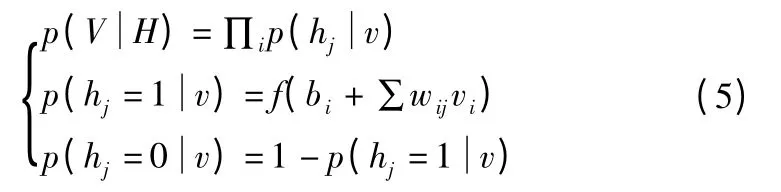
其中，p 为概率，f 为 sigmoid 激活函数.同理已知隐含层的情况下，得到可见层中第i 个节点的概率分布.因为样本训练集中的数据有云安全态势数据源标签，在顶层的RBM 训练时，可见层中除了显性神经元，还需要有代表分类标签的神经元，这里，对每一组训练数据相应的标签神经元被打开设为1，而其余的则被关闭设为0，综合上述得出DBN 训练过程算法.

4 基于IDE-DBN 算法的预测模型

由于DBN 网络隐含层单元的层数大都靠经验设置，而隐含层的相关参数对此比较敏感，如果选取不当可能带来预测结果精度严重下降够或训练时间过长等问题.针对这些问题，将差分进化算法(Differential evolution，DE)的核心思想融入到深度信念网络中，以达到精简网络结构，构建性能良好的深度学习模型.

基于IDE-DBN 的云安全态势预测模型的核心问题是确定隐节点层数，层间的权重与偏置.DE 算法改进后增强了全局搜索性能，进一步减少了局部极值［15］.基本思想是将用于云安全态势预测的DBN 网络的隐含层节点的各参数映射为差分矢量空间进化的初始目标个体并通过判断新个体和旧个体的适应度高低，汰弱留强，经过若干次迭代引导目标搜索向误差低的最优解逼近.DE 算法的数学描述如公式(6)所示［16］:

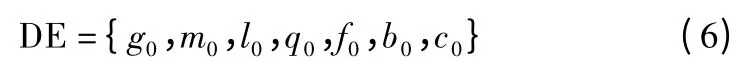
其中，g0为以DBN 网络的隐含层节点数，m0为DBN 隐含层参数，l0为种群规模，q0为个体的适应度函数，并定义三种操作:f0为复制操作，b0为交叉操作，c0为变异操作.

4.1 标准 DE 算法

标准DE 算法主要过程如图4 所示.

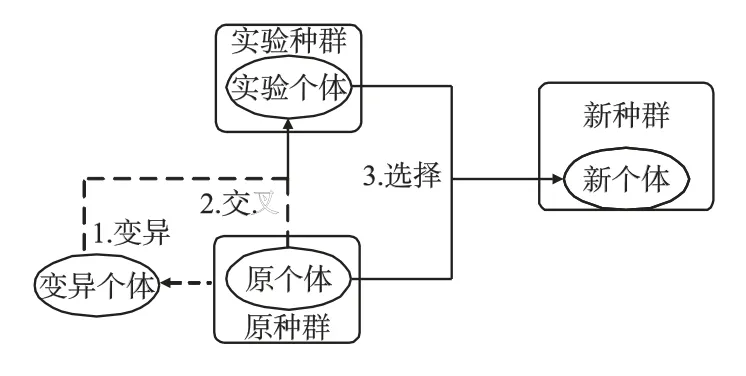
图4 标准DE 算法流程Fig.4 Standard DE algorithm flow

标准DE 算法中父代个体之间生成差分矢量，并将其叠加到随机一个目标个体上，通过对新的子代个体与父代个体进行交叉和选择操作，保留最优个体并添加到下一代种群中.算法的优化是在搜索空间不断变换的过程，易陷入局部最优，因此本文对交叉过程做出了改进.种群初始化:设NP 表示种群规模，D 表示个体维数，在问题决策空间按照公式(7)所示随机产生初代种群.

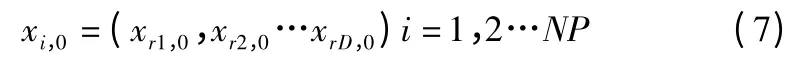
其中，xi，0为第0 代种群第i 个个体，个体在每一维上按照如公式(8)取值.

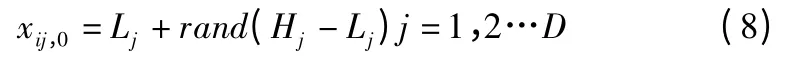
其中，(Hj，Lj)表示第 j 维的取值范围，xij，0表示初始代第 i 个体的第 j 维分量，rand 表示在区间(0，1)上均匀分布的随机数.

变异:初始化后，DE 算法通过对种群进行变异和重组操作来产生一个由NP 个实验向量构成的种群.对目标个体扰动产生变异个体，常见的变异策略有:DE/rand/1 策略中差分变异操作将一个可缩放的且随机选取的向量增加给一个第三方向量，如公式(9)所示.

DE/best/1 策略中，差分变异操作与一个可缩放的且随机选取的向量增加给基向量在当前群体表现最好的向量，如公式(10)所示.

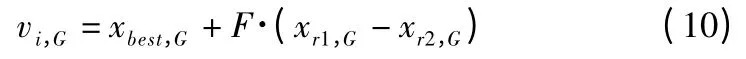
DE/current-to-best/1 策略中差分变异操作与两个可缩放的随机选取的向量增加给第三方向量，且矢量差中包含基向量在当前群体表现最好的向量，如公式(11)所示.

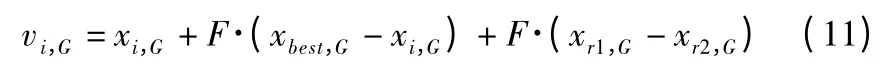
交叉:父代个体和变异个体进行交叉操作得到实验个体.

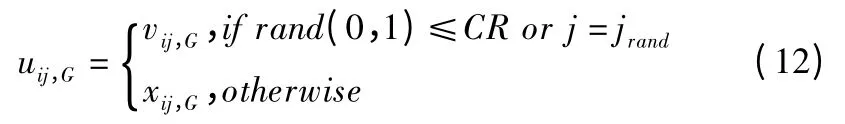
选择:基于贪婪原则选择实验个体和父代个体，优秀的个体将进入下一代.

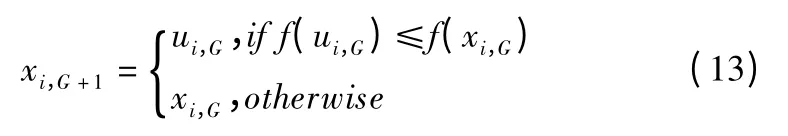
4.2 自适应机制

差分矢量实际上是对变异矢量xri，G各维决策变量的扰动［17］，F 控制扰动量的程度，如果生成的差分矢量在搜索空间相隔比较近，F 应取较大值，否则扰动量太小在进化初期不利于全局搜索，如果生成的差分矢量在搜索空间相隔比较远，F 应取较小值，否则扰动量太大，在进化初期不利于局部搜索.F 的取值应根据生成差分矢量的两个个体矢量在空间的相对位置自适应的调整变化，来平衡局部搜索和全局搜索之间的矛盾.

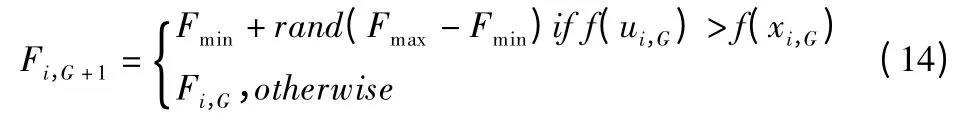
其中，Fi，G+1表示第 G+1 代第 i 个体的缩放因子，Fi，G表示第G 代的第i 个体的缩放因子，合适的缩放因子有利于产生存活率高的的子代个体.因此，通过记录历史最近一次的因子参数可以按照公式(15)产生新的Cri.

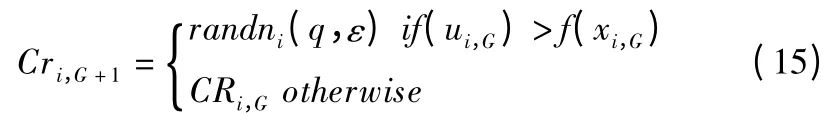
其中，Cri服从高斯分布，表示第 G 代第i 个体的交叉率，randni(q，ε)为平均值 q 和标准差 ε 的高斯分布.

4.3 二维旋转交叉算法

随着进化代数不断深入，标准DE 算法无法应对种群多样性的适应性变化以及在可行解空间内全局最优解无法保证收敛［18］.通过引入二维旋转交叉算法，使目标个体和变异个体周围产生子代的个体.设含有NP 个D 维个体的种群旋转半径如公式(16)所示.

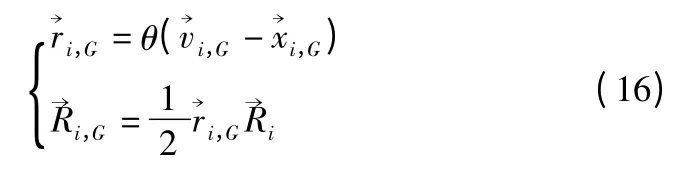
设定方向控制参数θ，其作用保证子代个体能够均匀的分布在变异个体和目标个体附近，当θ=1 时，交叉向量的方向从，当 θ=－1 时，向量反向.为目标个体和目标个体之间的距离，为分布在新子代附近的旋转半径，ω 为向量旋转的角，G 为迭代数，R→ 为控制旋转的矢量，其值如公式(17)所示.

C1为通用常量，R→ 的模随着G 的增加而减小，有利于增加搜索精确度和加速TRC-DE 算法的收敛性，调整控制矢量因子R'服从柯西分布如公式(18)所示.

R'为NP×D 的矩阵，其个体满足柯西分布，因为柯西分布拖尾较长，因此用柯西分布控制产生子代个体选择范围增加.

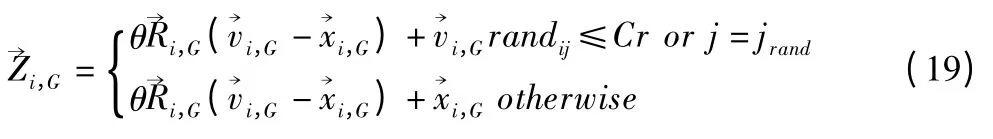
融入二维旋转交叉方式可以使增加子代个体种群多样性，综上分析得出基于二维旋转交叉的DE(TRC-DE)算法步骤如算法2 所示.

4.3.1 种群多样性的论证

为了说明引入二维旋转交叉算法如何提高标准DE 算法种群多样性和可收敛性的问题，通过二维空间内旋转向量的具体例子来证明:假设带入公式(16)得:

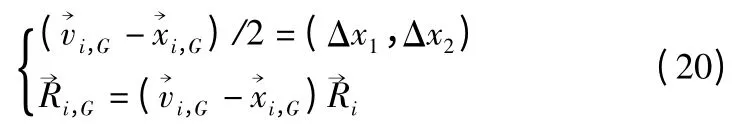
其中，Δx1=v1－x1，Δx2=v2－x2，旋转向量可以表示为(r1Δx1，r2Δx2)，旋转向量的模可以被表为:

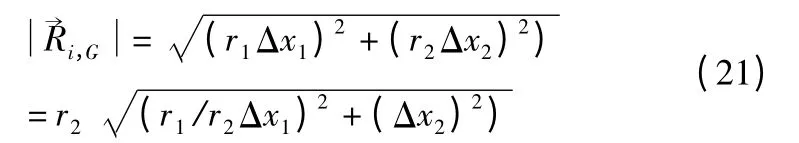
令r1≤r2，则的模可随着的坐标值不同而大小变化的旋转角度ω 可由公式(22)得到.

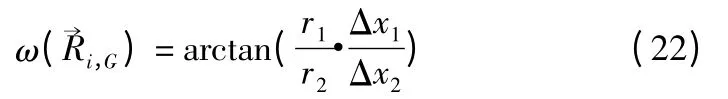
图5 二维旋转交叉原理示意图Fig.5 Diagram of two-dimensional rotation cross

在公式(22)中，有三种可能出现的情况:如果r1=r2，向量的方向和相同.如果r1＜r2，那么 ω 将比向量的角度大.如果r1＞r2那么角度ω 将比向量的角度小，旋转向量的模和ω 随着向量的坐标变化而变化.图5展示了二维旋转的具体过程.白色圆表示目标个体，白色矩形表示变异个体，灰色矩形表示二维旋转交叉产生的子代个体.TRC-DE 算法的搜索空间范围从种群个体Z1、Z2和种群个体Z3三个点扩展到以点Z2和连线的中间的圆点为半径的种群区域，同时得到一个新个体种群Z4，增加了种群多样性.通过逐步的迭代进化，种群区域半径会逐渐动态收缩，从而改善算法的收敛速度.

4.3.2 收敛性的论证

采用国际标准测试函数CEC2013 对TRC-DE 算法的收敛性进行测试.从CEC2013 中选取10 种函数f1到f10，包括单峰分布函数与多峰分布函数.以适应度评价Rastrigin 函数为例，如表2 所示.通过测试函数的平均值和标准差与标准DE算法做收敛性对比分析.

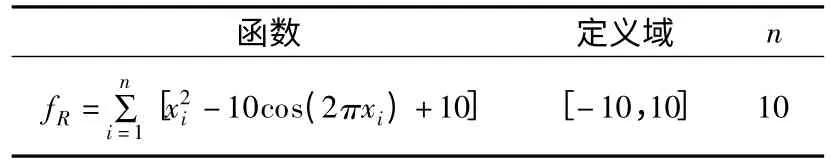
表2 测试函数Table 2 Test functions

相关测试参数设置:目标种群个数NP=1000，最大迭代数Epoch_size=1500.标准 DE 算法中，取缩放因子 F=0.5，交叉概率 CR=0.7;在 TRC-DE 中，取 F=0.65，CR=0.6.从表3得在DE/rand/变异策略下，TRC-DE 在平均值和标准差均低于标准DE，且收敛精度比标准DE 算法高.基于适应度Rastrigin函数的TRC-DE 和标准DE 算法寻优过程如图6 所示.

图6 两种算法的收敛曲线图Fig.6 Convergence curve of the two algorithms

从图6 中看出TRC-DE 算法随着迭代次数的增加以线性递减的方式可收敛到最优解，而标准DE 算法在Epoch_size＞500 后，由于适应度Rastrigin 评价函数存在多个局部极小值而 无法收敛.从表3对比结果可知标准DE在函数f2，f4，f7表现较好，但是在其他函数上优化效果较差，在f8函数上两者差别较小.TRC-DE 算法极大地改善了对单峰函数f1，f3以及多峰函数f5，f6，f9，f10上的全局寻优能力，优化率达到了60%.

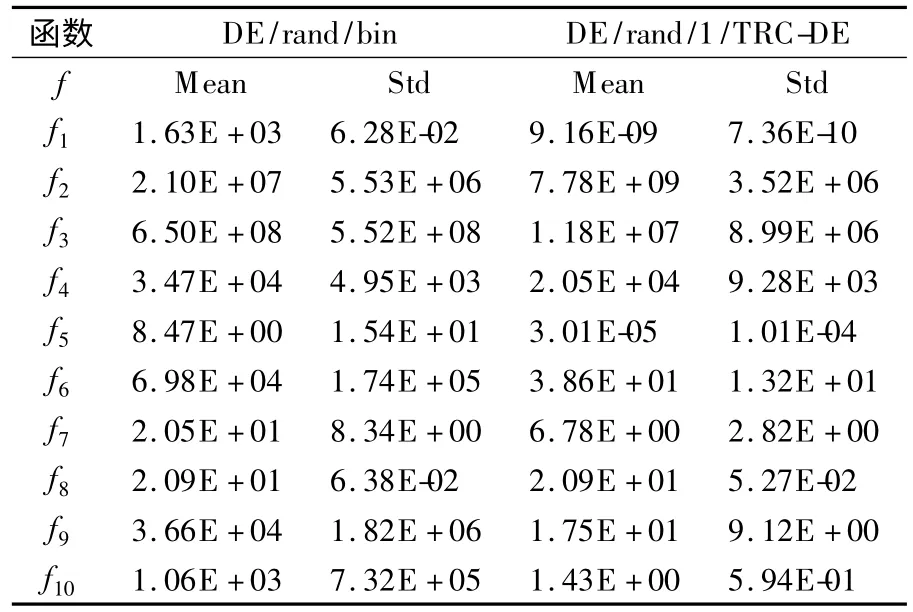
表3 测试函数输出结果对比Table 3 Comparisons of output results

4.4 IDE-DBN 算法

IDE-DBN 是将TRC-DE 算法与DBN 算法结合起来形成的组合算法，将DBN 的权值和偏置值视为种群，并以此完成变异、交叉和选择操作.

5 仿真分析

5.1 态势数据的收集

仿真试验在某大学私有云网络中心划分的子网内进行.将Netflow，Snort 和Nessus 等工具软件旁路接入子网主虚拟服务器，获取服务器实时安全运行的检测、扫描或日志信息.同时，在应用服务器上安装云性能监控工具听云Server PHP探针，通过听云Sys 实时获取云网络的平稳性指标数据.

首先，本文通过选取Netflow 流量数据、Snort 入侵检测日志和Nessus 扫描和分析后的日志作为态势主指标T1、T2 和T 3［11］的数据源，二级指标的关联字段如表4-表6所示.这三种数据来源基本涵盖了从数据流量、攻击威胁和潜在的系统漏洞等方面的信息，能够较为全面的反映了云网络的安全运行状态，为云安全态势预测提供数据源支持.

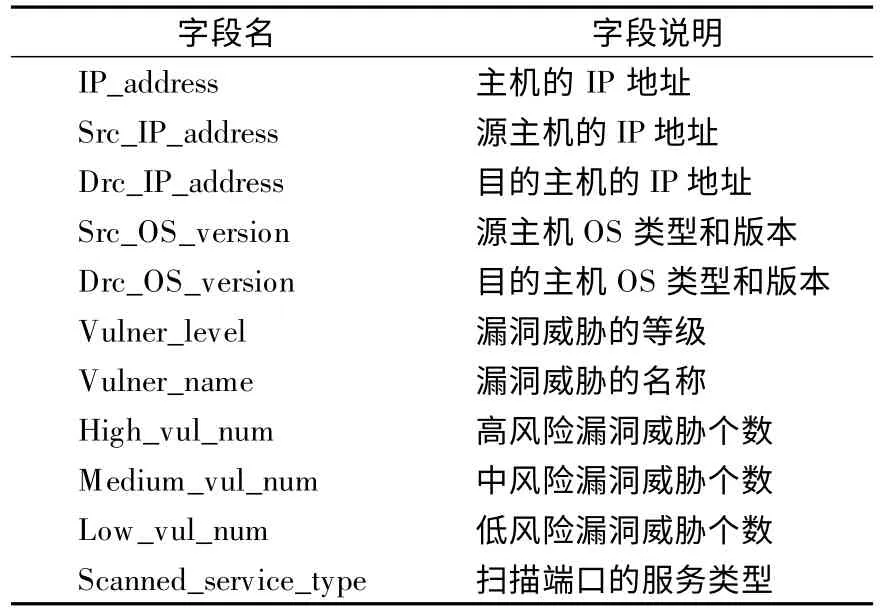
表4 脆弱性T1 的字段Table 4 Fields of vulnerability index

表5 生存性T2 字段Table 5 Fields of survivability index

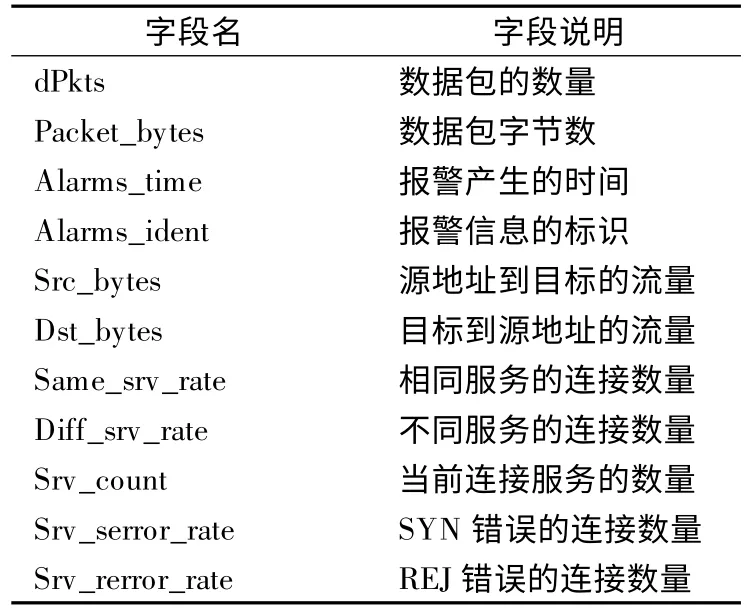
表6 威胁性T3 字段Table 6 Fields of threat index

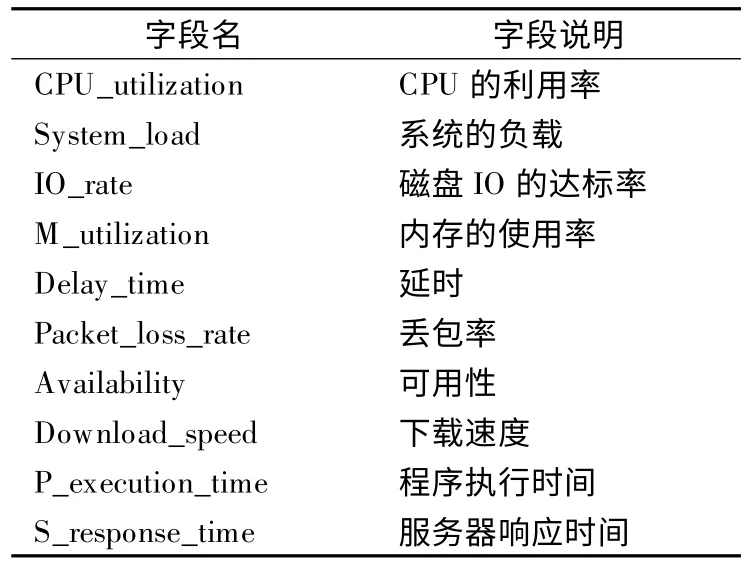
表7 运行平稳性T4 字段Table 7 Fields of running stability index

然后，通过听云Network 模拟真实用户发起持续的连接，在虚拟应用服务器中运行MySQL 数据库的增、删、改、查等操作及压力IO 程序，最后通过听云Server 和听云Sys 来获取云网络运行平稳性的各项测试值，二级指标的关联字段如表7 所示.

5.2 态势数据预处理

数据样本为2019 年3 月-2019 年4 月获取的数据，将收集到的数据分类成四个子表存储到数据库中，经过对原始数据平滑处理、噪声处理、态势评估［19］获得的安全态势值，然后利用IDE-DBN 模型进行训练，初始的训练参数及测试参数如表8 所示.

使用深度学习框架Tensorflow，利用 RBM 来构造DBN 初始网络.在程序实现上使用RBM 共用MLP 的参数，并且由RBM 执行预训练.为防止训练过程激活函数发生过拟合，DBN网络初始权值和偏置为0.1，最大迭代次数Epoch_size=1500，隐含层节点N=25，初始输入延迟为10ms.

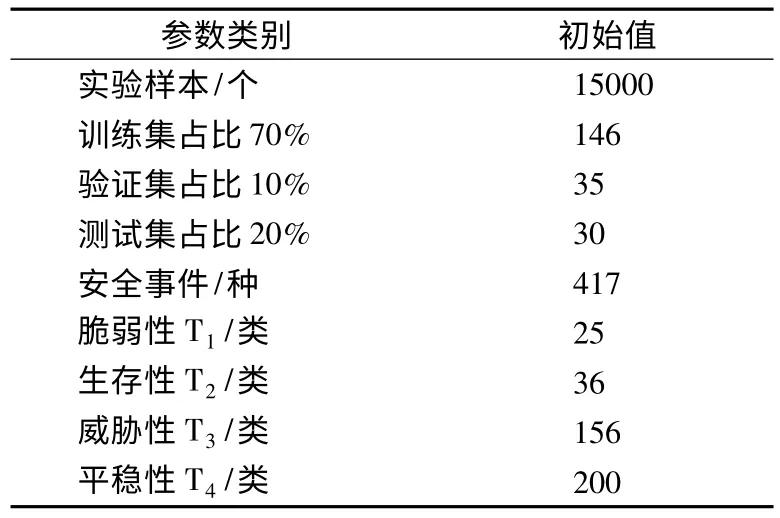
表8 初始训练与测试参数表Table 8 Initial training and test parameters

5.3 实验结果分析

预测结果目标值与实际值的对比如图7 所示.通过计算云安全态势预测模型的输出值和实际值的均方误差MSE 和均方根误差RMSE 以及相关性系数R，作为IDE-DBN 模型预测效果的评判指标依据.MSE 和 RMSE 值越小，说明 IDEDBN 模型预测精度就越高，R 值越逼近1，表明DBN 网络越逼近实际系统.or真实值，om为模型输出值，相关系数表示为如式(24)所示.

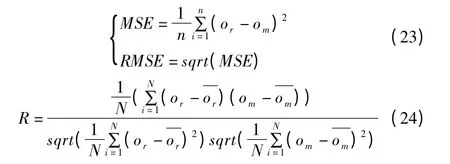
图7 输出值与实际值对比Fig.7 Comparisons of output value with actual value

图7 中，点线表示云安全态势真实值，实线表示预测值，Target 表示云安全态势输出级别.根据输出指标体系划分云安全态势等级，由此来判断云平台的受威胁程度.从图7 中可以看到在初期5h 左右态势输出等级大于0.2，云安全态势等级处于II 和III 级别，在随后的5 个小时云安全态势等级下降到I，因目前风险不高，安全应急检测阶段可通过安全分析工具实现对多源异构信息的批量采集、识别和关联分析，聚类入侵行为与风险点的异常特征.10h 云安全态势趋于平稳，20h达到最低级别I，此时云安全平台威胁程度最低，在第30h 处外部威胁到来态势等级达IV，85h 云安全等级为安全，但态势等级趋势为上升，云平台整体的安全态势趋于中度危险.预测结果显示:这种恶化趋势将会持续加剧，在100 小时对云平台的威胁达到最大级别V，这时需进入应急响应的抑制和根除阶段.可以采用主动诱骗或被动的日志审计、异常分析和漏洞检测等安全检查，制定应急策略并实施，在随后的阶段云安全态势等级趋于平稳，在120h 的时候态势等级处于安全状态.

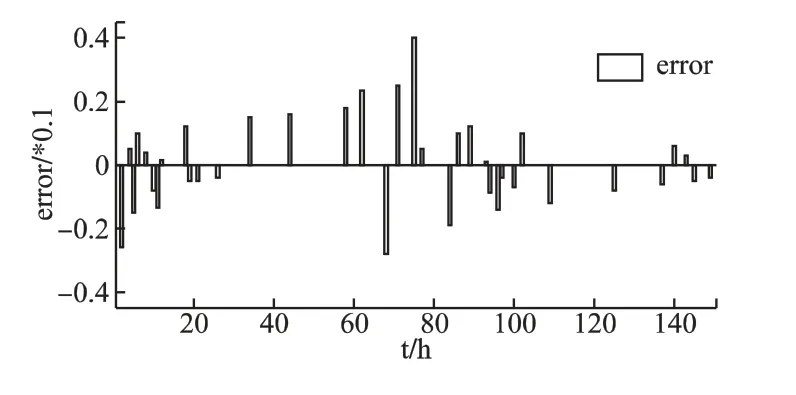
图8 预测模型输出值与实际目标值误差Fig.8 Error comparisons

从图8 可知预测前期(0-80h)阶段性误差维持在±1%到±4%之间，均方根误差RMSE≈0.0252 预测后期(80h 后)引入改进的DE 算法后，两者曲线拟合度较高，误差逐渐减小，阶段性误差维持在±2%以内，均方根误差RMSE≈0.0135.预测结果的发展趋势与实际结果基本相同且预测较为准确，DBN 网络预训练和全局微调迭代100 次后基本达到稳定性能，此时 MSE=0.0102，模型相关性系数 R=0.9365，预测结果如图9 所示.

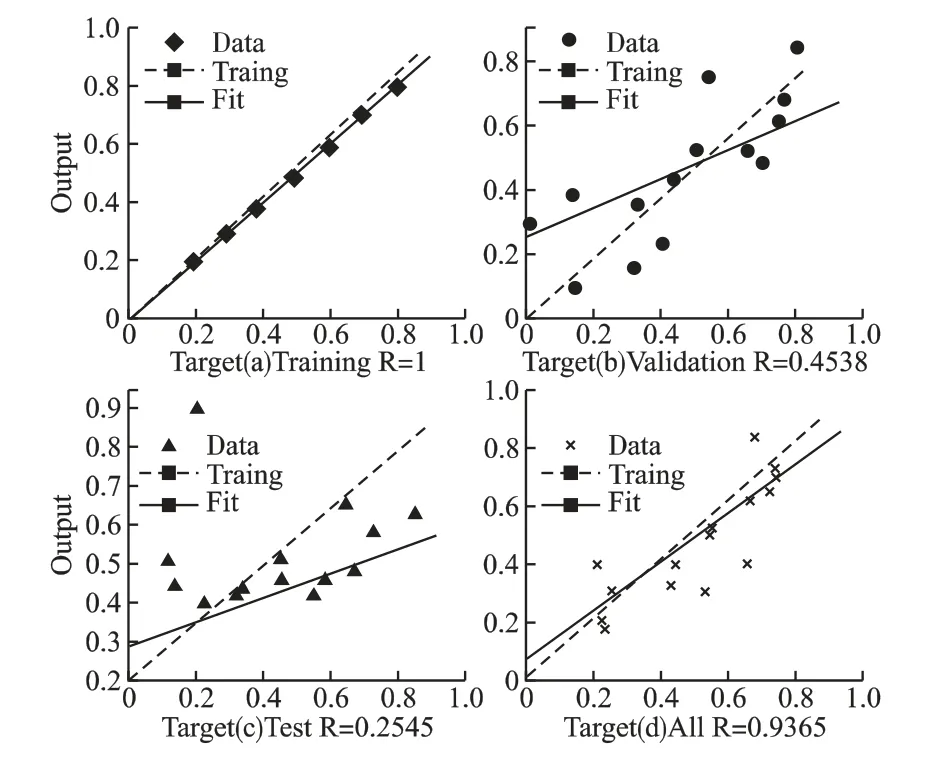
图9 预测模型结果相关性Fig.9 Relevances of prediction model results

实验将基于IDE-DBN 模型的云安全态势预测结果与RBF 网络预测模型和BP 网络预测模型进行对比，采用不同算法的神经网络云安全态势预测模型总体准确率和测试时间如表9 所示.

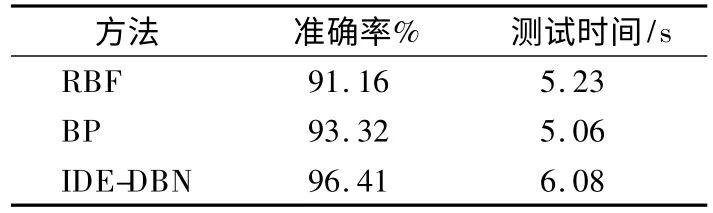
表9 准确率和测试时间Table 9 Accuracy and test time

由表9 和表10 可知，基于径向基函数RBF 的预测模型的准确率为 91.16%，MSE=0.09 和 R=0.74，而测试时间相对 IDE-DBN 模型降低了 1.02s.

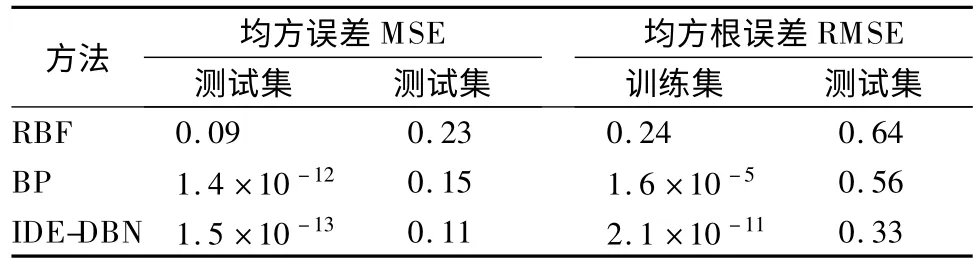
表10 均方误差和均方根误差Table 10 MSE and RMSE

基于BP 网络模型预测的云安全态势预测结果准确率为93.32%，训练集数据均方误差为 MSE=1.4×10－12，其均方根误差为 RMSE=1.6×10－5，由表11 可知，相关性系数 R=0.81，其预测准确率和模型输出相关性低于基于IDE-DBN 预测模型的准确率和R.

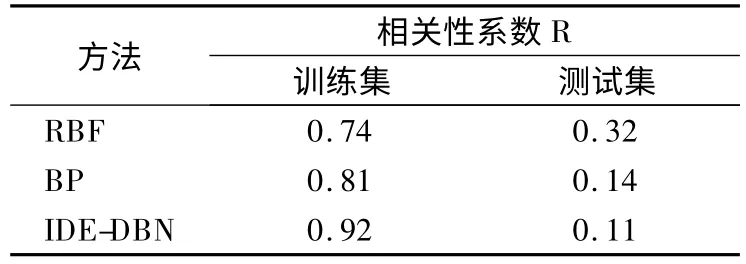
表11 相关性的比较Table 11 Comparisons of the correlation R

综上分析，相比RBF 和BP 模型，IDE-DBN 模型的预测准确率分别提高了5.25%和3.09%，但是因参数微调和预训练过程导致测试时间效率增加0.85s 和1.02s，有待进一步提高和改善.

6 结 论

云计算环境下态势数据多源，特征多维，数据量大，这就导致预测结果受到诸多云安全态势要素的影响.通过建立综合的态势评估指标体系，为提高云安全态势预测的准确度奠定了基础.然后，通过对云安全态势值划分等级，这有利于定量地对云环境的实时安全性做出直接判断.通过对态势数据样本在DBN 模型训练过程中引入改进的差分进化算法来优化隐含层的参数，提高了预测模型的准确度.所提模型为安全管理员提供了实时态势预测分析，能够提前预防和采取相应的应急措施，变被动防御为主动响应.下一步研究的重点是云安全态势预测的可视化平台以及分布式智能生态安全系统.