基于K-means聚类算法的桥梁结构真实模态筛选研究

尹红燕，刘东霞，唐 莉

(重庆交通职业学院，重庆 402247)

0 引言

随着我国桥梁结构的飞速发展，各种大型桥梁结构应运而生，随之而来的弊端是桥梁安全事故的发生频率日益增长，目前如何判别桥梁结构在运营阶段的健康状态[1]已经成为了一个十分重要的研究课题。实际工程中，常通过对桥梁结构进行动力监测[2]来实现对其的安全监测，因为一旦结构发生损伤[3]，则其自身的动力特性会发生不同程度的变化。基于此，提出了通过分析桥梁结构的固有频率、阻尼比以及模态振型[4]的变化情况来判别其健康状态。

随着桥梁跨度的不断增大、新型材料的使用以及环境因素的影响导致现有的模态参数识别算法[5]已不能很好地满足人们对结果精度的要求。随机子空间算法(Stochastic Subspace Identification-SSI)[6-7]作为主要识别算法之一，已有不少学者研究了如何辨识稳定图中的真假模态，包括汤宝平等[8]通过在参数识别过程中引入谱系聚类算法来完成模态参数的自动化识别；UBERTITN F等[9]利用谱系聚类分析法来辨识稳定图中的真假模态；章国稳等[10]将聚类算法运用于模态参数结果的筛选过程中，以辨识稳定图中的真假模态。

虽然这些算法能在不同程度上实现真实模态的智能化识别，但识别效果均不佳，其主要原因在于：在参数识别过程中忽略了结构自身真实模态[11]存在的一般规律。基于此，本研究以某试验桥梁为研究对象，首先通过分析大量稳定图中真假模态的存在形式来总结其存在的一般规律，其次基于K-means算法[12]提出了一种新的模态参数识别算法，最后将该算法运用于试验桥和实际桥梁结构中以验证算法的可信性。

1 DATA-SSI算法

随机子空间算法之所以被广泛运用于桥梁结构的模态参数识别中，其主要原因在于该算法相比其他参数识别算法而言有如下3方面的优点：(1)可直接将时域信号作为输入数据；(2)不会出现频率分辨率误差等问题；(3)识别的固有频率、阻尼比以及模态振型均能满足实际工程的需求。

该算法共分两类，分别是基于数据驱动的随机子空间算法[13](Data driven Stochastic Subspace Identification,DATA-SSI)和基于协方差驱动的随机子空间算法[14](Covariance driven Stochastic Subspace Identification,COV-SSI)。对比这两种算法的基本原理和计算效率可知：

(1)DATA-SSI算法在数据缩减方面具有更高的效率，因为该算法是通过正交投影的方式对 Hankel矩阵中的数据进行缩减；而COV-SSI算法则是利用协方差的方式进行数据的缩减。

(2)DATA-SSI算法在计算效率方面具有更高的效率，因为该算法的计算过程中仅涉及一次QR分解；而COV-SSI算法过程中需对Toeplitz进行多个协方差计算。

鉴于上述原因可知：DATA-SSI算法更适应于实现模态参数的自动化识别，所以本研究以该算法为研究对象进行模态参数自动化识别研究。以下将简单介绍基于数据驱动的随机子空间算法的基本理论。

1.1 基本原理

DATA-SSI算法的大致计算步骤如下：

Step1：利用公式(1)建立Hankel矩阵，Yp为“过去”信息，Yf为“将来”信息；

(1)

Step2：QR分解

利用公式(2)对Hankel矩阵进行QR分解；

(2)

Step3：奇异值分解

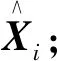
(3)

Step4：特征值分解

利用公式(4)对系统矩阵A进行特征值分解；

A=eAcΔt，

(4)

Step5：模态参数计算

利用公式(5)计算模态参数结果；

Φi=CiΨi，

(5)

1.2 稳定图定阶

在利用DATA-SSI算法进行参数识别时，需事先明确系统的真实阶次，阶次过高过低都会导致识别的结果不可信，因为过高时会伴随虚假模态的产生；过低时会伴随模态遗漏现象的发生。基于此，可利用稳定图法[15]对系统进行真实阶次的确定，该方法的基本原理是以频率为横坐标，系统阶次为纵坐标，将各阶次对应的极点绘于同一图中，并分析前后两阶对应各参数是否满足公式(6)所示容差，当满足时则可判定该阶次为系统的真实阶次。

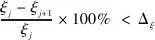
(1-MAC(j,j+1))×100%<Δψ(振型容差)，

(6)

式中，j为阶次数；f，ξ，ψ分别为频率值、阻尼比及振型；MAC为模态置信因子。关于容差的具体取值，文献[16]对其进行了深入研究，根据该文献可将频率容差定为1%；振型容差和阻尼比容差为5%。图1为稳定图定阶的一般流程图。

图1 稳定图定阶原理Fig.1 Principle of stable diagram order determination

2 桥梁结构的真实模态

为了分析桥梁结构真实模态存在的一般规律，以某大型斜拉桥振动台试验为研究对象，首先将各节点各时间段内的振动信号作为DATA-SSI算法的输入完成参数识别；并对比分析大量稳定图中模态参数的存在形式，进而总结出稳定图中真假模态的存在规律。

2.1 试验桥概况

该桥梁结构为斜拉桥，其跨度为(130+380+130)m，试验桥梁是以1∶20的比例对实桥进行比例缩放。桥型布置图、主梁的平面图如图2所示。桥梁结构各部分对应的材料情况如下：

(1)采用M15微粒混凝土模拟索塔和桥墩；

(2)采用直径为6 mm的圆钢模拟普通钢筋；

(3)采用10#钢丝模拟抗剪钢筋；

(4)采用厚度为5 mm的钢板模拟主梁结构和钢箱梁；

(5)采用直径为10 mm的钢丝绳模拟拉索。

2.2 传感器布置

桥梁结构建立于振动台上，试验过程中可通过振动台对其施加不同的激励，并利用事先布置在主梁上的加速度传感器采集各点对应的振动信号，传感器布置图如图3所示，主梁上共设置11个传感器。

图2 桥梁实景图(单位：cm)Fig.2 Real images of bridge(unit:cm)

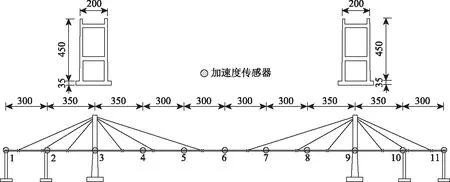
图3 加速度传感器布置图(单位：cm)Fig.3 Arrangement of acceleration sensors (unit: cm)

2.3 地震波及响应信号

输入地震波分为两类，分别是Chichi波和场地波(Sit波)，各地震波对应的输入方向、输入波形以及峰值加速度如表1所示。根据该表可知，根据地震波波形和峰值加速度的不同将振动台输入地震波分为6种工况。各工况下信号的采样频率均为256 Hz，采样时间为240 min。图4是G1工况下6#传感器在最开始20 s内对应的加速度响应信号时程图。

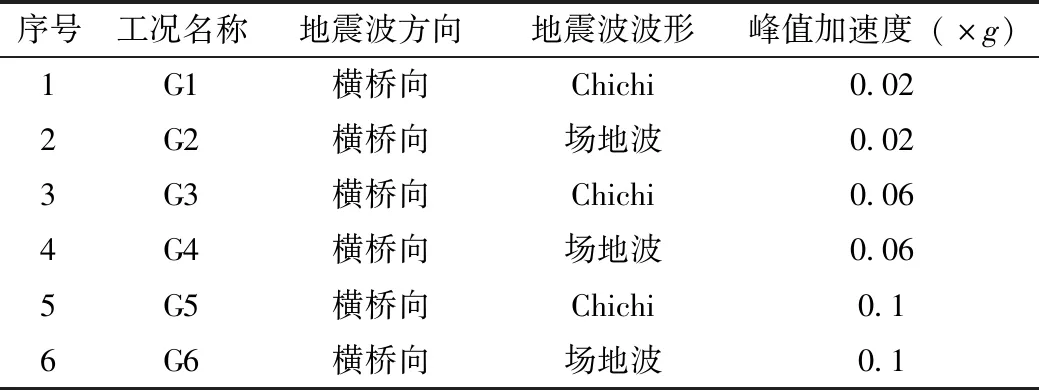
表1 试验工况表

2.4 真实模态的一般规律

以每分钟采集的响应信号为DATA-SSI算法的输入数据，即输入信号的矩阵大小为15 360×11(11代表共11个传感器)，即同一地震波可识别得到720幅稳定图，图5仅为G1工况下随机的3幅稳定图。

对比分析6种工况下共1 440幅稳定图，得到如下3点结论：

(1)同一工况的不同时间段内，稳定图中的稳定轴(真实模态)具有稳定性，即不会因为虚假模态的存在发生较大差异；

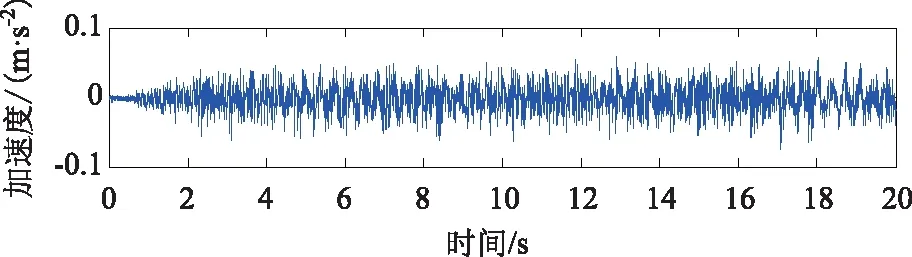
图4 加速度时程曲线Fig.4 Curve of acceleration vs. time

图5 稳定图Fig.5 Stability diagrams

(2)同一工况的不同时间段内，稳定图中的虚假模态具有不稳定性，即各稳定图中虚假模态的分布情况具有离散性；

(3)两种地震波识别所得真实模态具有互补性，即如果仅对试验桥进行一种地震波试验，则识别的真实模态会出现模态遗漏现象。

综合上述：对于某一固定的结构而言，其自身的动力特性参数具有时不变性，当该结构受到外界因素的影响而发生损伤时，其动力特性参数(真实模态) 会随之发生一定的变化。

3 真实模态的筛选

人为辨识稳定图中的真假模态不仅会耗费大量时间，还会导致辨识的结果不可信。基于此，可以利用多元统计学中的聚类算法[17-18]来从大量稳定图中筛选真实模态和虚假模态，通过引入K-means聚类算法的方式来辨识真假模态。之所以选择K-means聚类算法，是因为该聚类算法相比谱系聚类算法而言，不仅能实现不同维度数据的聚类，也能判别数据间是否属于同一类，还能筛选出同类的数据点。以下将详细介绍K-means算法的基本原理以及如何将其融入到模态参数识别的流程中。

3.1 K-means算法的基本原理

K-means算法的基本原理：按照样本之间的距离大小将样本集划分为K个簇，使得各簇内的点都尽可能得紧密聚集，进而保证簇间的距离尽可能得大。假定输入样本集D={x1,x2,…xm}，聚类的簇树为K，最大迭代次数为N，输出是簇划分C={C1,C2,…,Ck}。

该算法的详细步骤如下：

Step1：从样本集D中任意选择K个样本作为最初的K个质心向量：{u1,u2,…uk}。

Step2：对于各迭代次数n=1,2,…N。

(1)将簇划分C初始化为Ct=∅，t=1,2,…k；

(2)对于各样本i=1,2,…,m，计算样本xi和各个质心向量uj(j=1,2,…,k)的距离：

(7)

标记最小的dij所对应的类别为λi，并更新Cλi=Cλi∪{xi}；

(3)对于各簇树j=1,2,…,k，重新计算Cj中所有样本点的新质心uj，

(8)

(4)当K个质心向量均未变化时，则进行Step3。

Step3：输出簇划分C={C1,C2,…,Ck}。

3.2 真实模态的筛选

将K-means算法运用于辨识多幅稳定图中的真实模态，具体步骤如下：

Step1：基于1.2节所提稳定图定阶算法确定结构的真实系统阶次N；

Step2：利用1.1节所提DATA-SSI算法识别得到结构在多个时间段内的参数结果，假定参数结果共有NN组。通过不断的反复试验，建议NN≥300。定义每组参数结果Xi={Fi,Di,Mi}(i=1,2,…,NN)；

Fi=fi(m,n)，

Di=ξi(m,n)，

Mi=ψi(m,n,c)，

m=1,2,…,N，

n=1,2,…,j，

c=1,2,…,g，

(9)

式中，fi为第i组参数结果中的频率二维数据矩阵(m×n)；ξi为第i组参数结果中的阻尼比二维数据矩阵(m×n)；ψi为第i组参数结果中的阻尼比三维数据矩阵(m×n×c)；m为矩阵的行数，等于系统的阶次N；f为传感器个数，即输入信号的例数。

Step3：基于K-means算法实现第1组参数结果X1={F1,D1,M1}与第2组参数结果X2={F2,D2,M2}间的同类项聚类，步骤如下：

(1)频率矩阵f1与频率矩阵f2间的聚类

基于K-means算法对f1中的第i列频率向量f1(m,i)(m=1,2,…,N)与f2中的第j列频率向量f2(m,j)(m=1,2,…,N)进行聚类，由于频率矩阵中存在为0的项，则需首先剔除向量中的0项，得到重构的向量f′1(m,i)(m=1,2,…,N)和f′2(m,j)(m=1,2,…,N)。

基于以上步骤实现频率矩阵f1与f2的频率聚类，即将所有的同类模态都聚为一类，同时将所有的聚类模态与未聚类的模态组成新的参数结果f1-2。

(2)利用阻尼比进一步验证频率聚类结果

假定第1组频率参数结果的第1列模态f1(m,1)和第2组频率参数结果的第1列模态f2(m,1)为同一模态，则基于频率聚类的原理验算两者对应的阻尼比结果是否属于同类项，即验证ξ1(m,1)(m=1,2,…,N)和ξ2(m,1)(m=1,2,…,N)所得的簇划分结果是否满足95%的原则。当满足上述条件时，则认为f1(m,1)和f2(m,1)为同类模态予以保留，反之则剔除这组聚类结果。

(3)基于稳定图法的原理验证步骤(1)和步骤(2)所得的同类模态

(10)

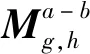
基于步骤(1)～(3)完成第1组参数结果X1={F1,D1,M1}与第2组参数结果X2={F2,D2,M2}间的所有聚类，将聚类后的模态和未聚类的所有模态整合到一起，并定义为新的参数结果X1-2。

Step4：基于Step3完成X1-2与X3间的同类模态聚类，得到新的聚类参数结果X2-3；以此类推，完成NN组参数结果的同类聚类，得到X(NN-1)-NN。

Step5：由于X(NN-1)-NN中的各阶模态有的是从X1到XNN中通过聚类得到的，有的则是非聚类的模态。为了进一步筛选出最为真实的模态，可首先统计X(NN-1)-NN中各聚类模态的聚类项数(即：该聚类模态是由多少组模态聚类组成的)；其次选择聚类项数大于0.85NN的模态，并将其绘制于最终的稳定图中；同时为了使识别所得的模态参数包含所有聚类项，所以取同类模态的均值作为最终的稳定轴绘制于稳定图中，进而得到最终的聚类稳定图。

梳理上述所有步骤，可得真实模态辨识流程，如图6所示。

图6 真实模态辨识流程Fig.6 Flowchart of real mode identification

4 试验桥参数识别

4.1 有限元结果

采用MIDAS软件建立2.1节所提试验桥梁结构的三维有限元模型，其中桥墩、索塔以及主梁对应的截面均采用纤维截面，且单元采用非线性梁柱单元(Nonlinear Beam-Column Elements)，采用桁架(Truss)单元模拟拉索；支座为盆式橡胶支座，且利用零长度单元(Zero-Length Element)模拟；混凝土的本构采用Concrete02 Material材料，钢筋本构采用Steel02材料。全桥模型如图7所示。

经特征值分析可获得其固有阶频率值和模态振型图，本研究仅仅罗列了其前7阶频率值和前4阶模态振型，频率值如表2所示，振型图如图8所示。

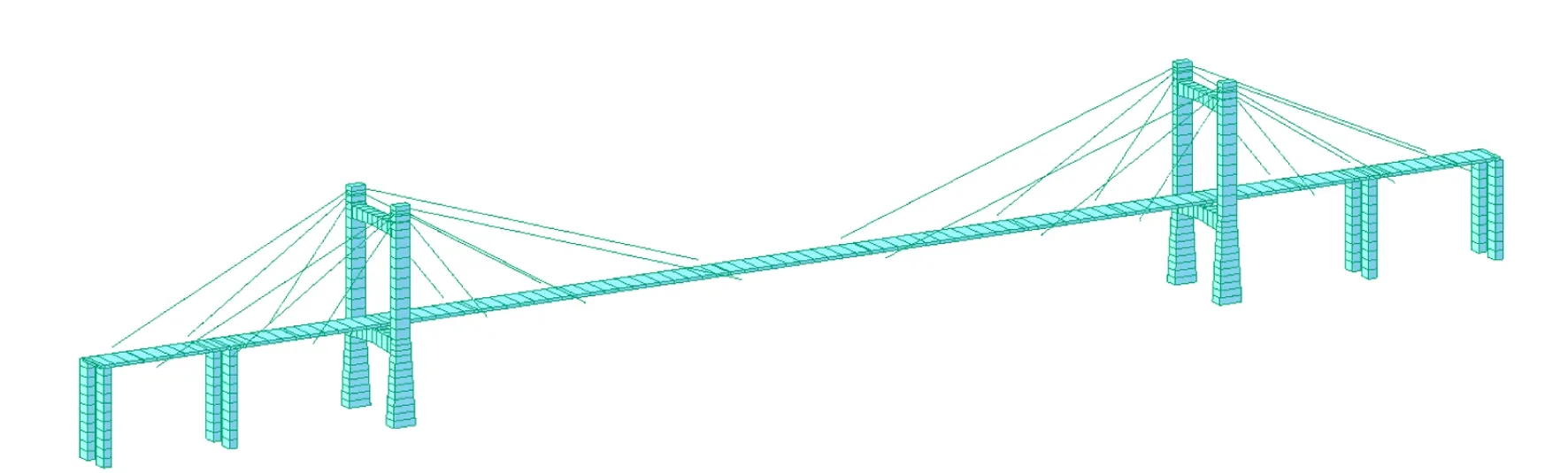
图7 全桥模型(MIDAS)Fig.7 Bridge model (MIDAS)

表2 自振频率(单位：Hz)

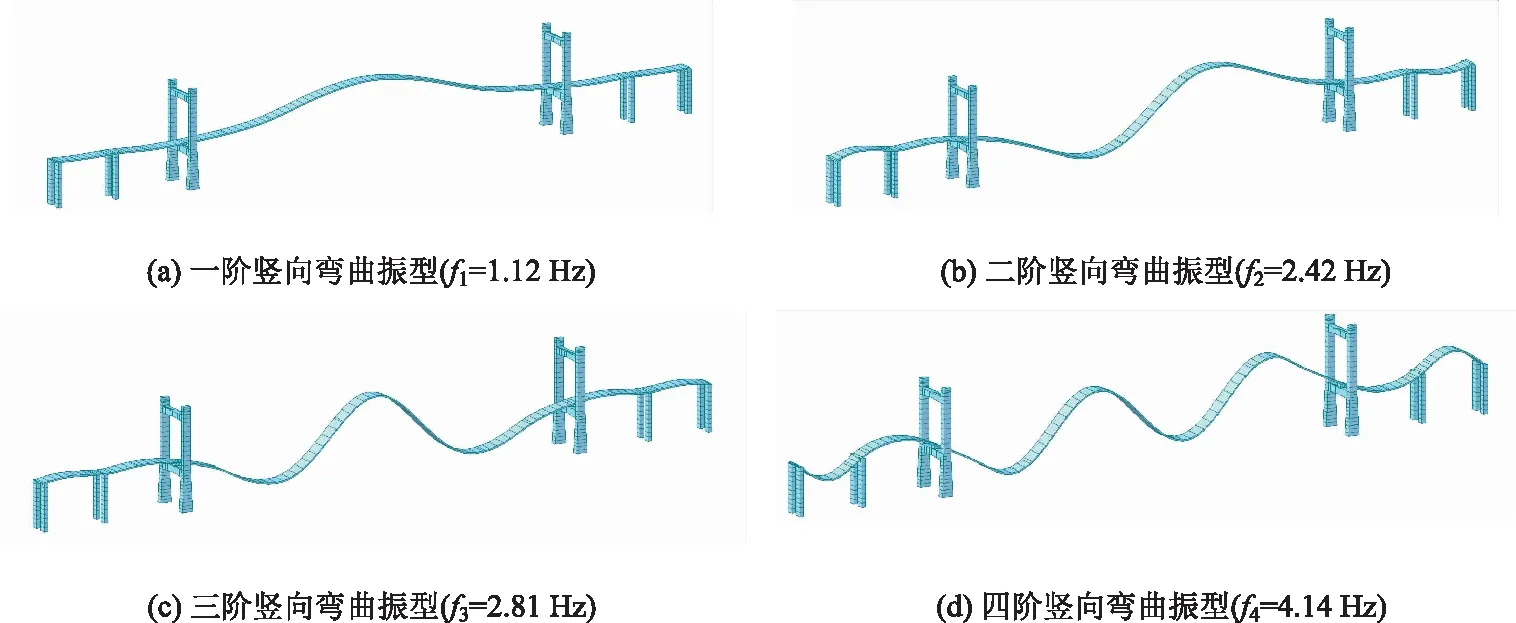
图8 前4阶模态振型图(MIDAS)Fig.8 Mode shapes of the first 4 orders (MIDAS)

4.2 识别结果

由于该桥梁结构的输入地震波共分两类，分别为Chichi波和场地波(Sit波)，信号采集时间为240 min，则以每分钟对应的响应信号为参数识别的输入数据，即每种地震波可得720幅稳定图。基于第3节所提真实模态筛选算法对这1 440幅稳定图进行辨识，绘制出最终的聚类稳定图，如图9所示。

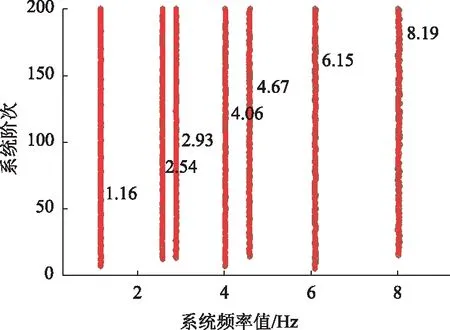
图9 聚类稳定图Fig.9 Clustering stability diagram

将图9中的各阶频率值与表2中MIDAS所得理论频率值作对比分析，结果如表3所示。

表3 频率对比

根据该表可得如下结论：

(1)本研究所提真假模态的一般规律具有可信性，且所提算法不仅能有效地辨识出桥梁的真实模态和虚假模态，还能有效避免模态遗漏现象的发生；

(2)识别所得频率值与MIDAS有限元软件所得理论值间的差值百分比在[-4.3%,4.96%]，验证了所提算法具有可信性。

为进一步验证识别所得模态振型同样具有可信性，绘制了该试验桥的前3阶二维模态振型图和三维模态振型图，如图10所示。将其与MIDAS有限元软件特征值分析所得的前3阶模态振型(图8)作对比，结果表明：本研究算法识别的模态振型图与理论模态振型图具有较高的相似度。

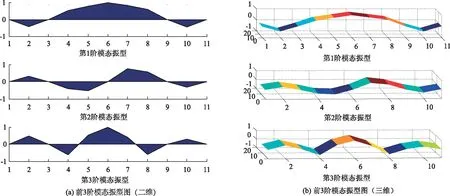
图10 前3阶模态振型图Fig.10 Mode shapes of the first 3 orders

之所以没有对阻尼比的结果进行对比分析，主要是因为结构的阻尼比受环境因素的影响很大，且人们对其的认知水平还比较有限。同时在MIDAS模型计算中采用的假定与实际工程结构间存在一定的差异。基于此，本研究仅对比分析了试验桥的固有频率值和模态振型结果。

5 某大型斜拉桥参数识别

5.1 实桥工程概况

为验证所提算法不仅能运用于试验桥梁，还能适用于实际桥梁结构。以重庆市某大型悬浮体系斜拉桥为识别对象，其主跨为330 m，边跨为149 m。其主梁上共设置有11处加速度传感器，桥跨布置图及传感器位置图如图11所示，其中主梁上的圆圈为传感器的大致布置位置。加速度信号的采样频率为1 s 80次，即频率为80 Hz。图12为主梁上某一传感器在随机50 s内采集到的信号时程图。

图11 桥跨布置图(单位：cm)Fig.11 Layout of bridge spans(unit:cm)

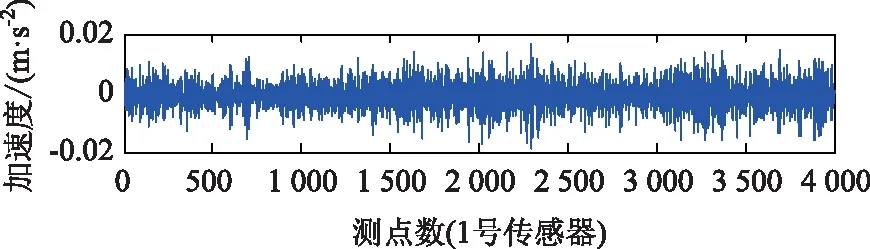
图12 加速度响应信号时程Fig.12 Time history of acceleration response signal

5.2 自振频率理论值

在主梁的主跨跨中采用跳车激振的方式产生激励，即通过汽车后轮越过带有坡面的三角横木(高度约12 cm)，利用车轮落下对结构的冲击来激励桥梁振动；并利用加速度传感器收集结构自振信号，最后对脉动信号进行分析识别得到其自振频率，跳车自振频谱图如图13所示，图中横坐标为频率值，纵坐标为对应的加速度值。

图13 实测跳车自振频谱图Fig.13 Actual frequency spectrum of jumps off

5.3 参数识别结果

利用加速度传感器采集斜拉桥在2019年4月份的所有加速度信号，并以每小时对应的响应信号作为参数识别的输入数据，即4月份30天可识别得到720幅稳定图。基于第3节所提真实模态筛选算法对这720幅稳定图进行辨识，绘制出最终的聚类稳定图，如图14所示。

图14 稳定图Fig.14 Stability diagram

将稳定图中前6阶频率值与跳车自振频率谱图中的频率值进行对比分析，得到表4所示结果，分析表中数据可知，识别所得频率值与跳车试验所得频率值间的差值百分比在[-4.7%,6.5%]，验证了本研究算法的识别结果具有可信性。

表4 频率结果对比

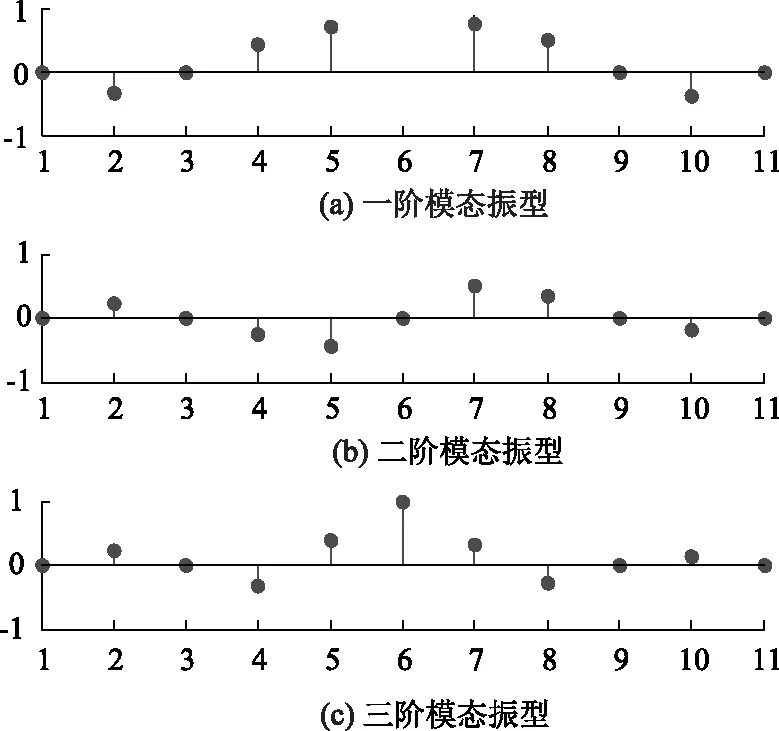
图15 前3阶模态振型图(二维)Fig.15 Mode shapes of the first 3 orders (2D)

图15和图16分别是该斜拉桥的前3阶二维模态振型图和三维模态振型图，将其与理论模态振型图作对比分析，可知识别所得模态振型与理论振型图具有较高的相似度。

图16 前3阶模态振型图(三维)Fig.16 Mode shapes of the first 3 orders (3D)

6 结论

本研究首先基于某试验桥结构分析了稳定图中真假模态的一般规律，其次通过在参数识别的过程中引入“K-means聚类算法”来实现稳定图中真假模态的智能化辨识,最后将所提算法运用于识别某试验和某实桥的模态参数，并将结果与理论值作对比，结果表明：

(1)所提真假模态的存在规律具有可信性，即结构的真实模态在结构未受损伤时具有稳定性，而虚假模态则会随着时间的变化发生变化，呈现的现象是在各稳定图中具有不稳定性和离散性；

(2)K-means算法能够实现多幅稳定图中同类模态参数的聚类完成真假模态的智能化筛选；

(3)本研究算法不仅适用于试验桥的模态参数识别，还适用于实桥结构的模态参数识别，且识别结果均具有较高的可信性。