鞅极大算子的一类四权弱型不等式
任颜波 张二鑫 王静
(河南科技大学数学与统计学院,洛阳,471023)
1 引言
Muckenhoupt[1]证明了Hardy-Littlewood极大函数的两权弱(p,p)型不等式成立当且仅当权满足Αp条件(1 在鞅论中, 与Hardy-Littlewood极大函数对应的是鞅Doob极大算子, 它们之间存在诸多类似的性质. 鞅极大算子的加权理论伴随着Hardy-Littlewood极大函数加权理论的发展而发展, 如今已成为鞅论的重要组成部分. 这里仅介绍与本文相关的部分工作. 1986年,龙瑞麟和彭立中研究了关于鞅极大算子的两权弱(p,q)型不等式, 得到其成立的充分必要条件[13]. 2003年, Kikuchi研究了鞅极大算子的两权弱(Φ,Φ)型不等式[9], 鞅极大算子的两权弱(Φ1,Φ2)型不等式分别在[10]和[11]中被研究. 最近, 任颜波研究了鞅极大算子的四权弱(Φ1,Φ2)型不等式, 得到其成立的一些充分必要条件[16]. 本文进一步研究加权不等式 (1.1) 在本文中, 我们充分利用条件期望的性质和Young不等式, 给出加权不等式(1.1)成立的一些新的充要条件. 特别地,我们得到它对偶形式的加权不等式, 从而推广已有的相关结果. 全文由三部分组成. 在下一节中将给出本文所需要的一些基本知识. 在第三节中将给出主要结果以及它们的证明. (ii) 0 φ的右连续逆定义为ψ(t)=inf{s∈(0,∞):φ(s)≥t},t∈(0,∞). 称 为函数Φ的补函数. Ψ为N-函数当且仅当Φ为N-函数,它们满足Young不等式 st≤Φ(s)+Ψ(t). 若(Φ,Ψ)为一对互补的N-函数, 则有 (2.1) 有关鞅理论和Orlicz空间理论的更多详细知识, 读者可参考[16,17,20]. 在本文中, 权意指几乎处处为正的可积随机变量. 我们分别用和表示非负整数的集合和整数的集合. 用C和C1等来表示正的常数, 允许在不同的地方取不同的值. 引理1设(Φ1,Ψ1)和(Φ2,Ψ2)是两对互补的N-函数,ωi(i=1,2,3,4)为权, 则以下三条等价: (i)存在与f=(fn)n≥0∈M无关的常数C1>0, 使得 (3.1) (ii)存在与f=(fn)n≥0∈M无关的常数C2>0, 使得 (iii)存在与f=(fn)n≥0∈M无关的常数C3>0, 使得 证明下面证明(i)⟹(ii)⟹(iii)⟹(i). (i)⟹(ii). 设(fn)n≥0∈M. 对于任意的A∈Fn和λ∈(0,∞), 由(3.1)式有 其中上式中的χ(A)表示集合A的特征函数, 从而有 对于任意的k∈, 令Bk={2k<|fn|≤2k+1}⊆{2k<|fn|}, 则对于任意的B∈Fn, 有 从而有 (ii)⟹(iii). 显然. (iii)⟹(i). 对λ∈(0,∞), 定义τ=inf{n∈:|fn|>λ}∈T, infØ=∞. 则{τ<∞}={f*>λ}, 且在{τ<∞}上有|fτ|>λ. 由(iii)可以得到 ≤C3 引理证毕. 引理2设A为F的一个子σ-代数, (Φ1,Ψ1)和(Φ2,Ψ2)是两对互补的N-函数,ωi(i=1,2,3,4)为权, 则以下两条等价: (i)存在常数C>0, 对任意正的随机变量x, 有 (3.2) (ii)存在常数C1>0, 对任意正的随机变量x, 有 (3.3) 证明(i)⟹(ii). 对任意k∈, 令由Young不等式, (3.2)式和(2.1)式, 得 再令k→∞, 便可得到(3.3). (ii)⟹(i)与(i)⟹(ii)类似, 这里不再赘述. 引理证毕. 引理3[16]设(Φ1,Ψ1)和(Φ2,Ψ2)是两对互补的N-函数,ωi(i=1,2,3,4)为权, 则以下诸条等价: (i)存在与f=(fn)n≥0∈M无关的常数C1>0, 使得 (ii)存在与f=(fn)n≥0∈M无关的常数C2>0, 使得 (Φ1(|fn|ω1)ω2|Fn)≤C2(Φ2(C2|f∞|ω3)ω4|Fn)a.e. ∀n∈; (iii)存在与f=(fn)n≥0∈M无关的常数C3>0, 使得 (Φ1(|fτ|ω1)ω2|Fτ)≤C3(Φ2(C3|f∞|ω3)ω4|Fτ)a.e. ∀τ∈T; (iv)存在常数C4>0和ε>0, 使得对任意正的Fn-可测的随机变量λ, 有 (v)存在常数C5>0和ε1>0, 使得对任意正的Fn-可测的随机变量λ, 有 ∀n∈. 由引理1-3, 我们可得到如下定理: 定理1设(Φ1,Ψ1)和(Φ2,Ψ2)是两对互补的N-函数,ωi(i=1,2,3,4)为权, 则以下诸条等价: (i)存在与f=(fn)n≥0∈M无关的常数C1>0, 使得 (ii) 存在与f=(fn)n≥0∈M无关的常数C2>0, 使得 (iii)存在与f=(fn)n≥0∈M无关的常数C3>0, 使得 (iv)存在与f=(fn)n≥0∈M无关的常数C4>0, 使得 (v)存在与f=(fn)n≥0∈M无关的常数C5>0, 使得 (Φ1(|fn|ω1)ω2|Fn)≤C5(Φ2(C5|f∞|ω3)ω4|Fn)a.e. ∀n∈; (vi)存在与f=(fn)n≥0∈无关的常数C6>0, 使得 (Φ1(|fτ|ω1)ω2|Fτ)≤C6(Φ2(C6|f∞|ω3)ω4|Fτ)a.e. ∀τ∈T; (vii)存在常数C7>0和ε>0, 使得对任意正的Fn-可测的随机变量λ, 有 (viii)存在常数C8>0和ε1>0, 使得对任意正的Fn-可测的随机变量λ, 有 ∀n∈.

2 预备知识


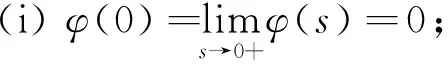

3 主要结果及证明